Термин считается
нераспределённым(неразвёрнутым, неисчерпанным, взятым не в полном объёме), если в суждении речь идёт не обо всех объектах, входящих в объём этого термина. Нераспределённый термин обозначается знаком «–», а на схемах Эйлера изображается неполным кругом (кругом, который содержит в себе другой круг (рис. 23,
a) или пересекается с другим кругом (рис. 23,
б).
Например, в суждении: «
Все акулы (S) являются хищниками (Р)», – речь идёт обо всех акулах, значит, субъект этого суждения распределён.
Однако в данном суждении речь идёт не обо всех хищниках, а только о части хищников (именно о тех, которые являются акулами), следовательно, предикат указанного суждения нераспределён. Изобразив отношения между субъектом и предикатом (которые находятся в отношении подчинения) рассмотренного суждения схемами Эйлера, увидим, что распределённому термину (субъекту «
акулы») соответствует полный круг, а нераспределённому (предикату «
хищники») – неполный (попадающий в него круг субъекта как бы вырезает из него какую-то часть):
Распределённость терминов в простых суждениях может быть различной в зависимости от вида суждения и характера отношений между его субъектом и предикатом. В табл. 4 представлены все случаи распределённости терминов в простых суждениях:
Здесь рассмотрены все четыре вида простых суждений и все возможные случаи отношений между субъектом и предикатом в них (см. раздел 2. 2). Обратите внимание на суждения вида
O, в котором субъект и предикат находятся в отношении пересечения. Несмотря на пересекающиеся круги на схеме Эйлера, субъект данного суждения нераспределён, а предикат распределён. Почему так получается? Выше мы говорили о том, что пересекающиеся на схеме круги Эйлера обозначают нераспределённые термины. Штриховкой показана та часть субъекта, о которой идёт речь в суждении (в данном случае – о школьниках, которые спортсменами не являются), в силу чего круг, обозначающий на схеме Эйлера предикат, остался полным (круг, обозначающий субъект, не отрезает от него какую-то часть, как это происходит в суждении вида
I, где субъект и предикат находятся в отношении пересечения).
Итак, мы видим, что субъект всегда распределён в суждениях вида
Aи
Eи всегда не распределён в суждениях вида
Iи
O, а предикат всегда распределён в суждениях вида
Eи
O, но в суждениях вида
Aи
Iон может быть как распределённым, так и нераспределённым в зависимости от характера отношений между ним и субъектом в этих суждениях.
Проще всего устанавливать распределённость терминов в простых суждениях с помощью схем Эйлера (все случаи распределённости из таблицы запоминать совсем не обязательно). Достаточно уметь определять вид отношений между субъектом и предикатом в предложенном суждении и изображать их круговыми схемами. Далее ещё проще – полный круг, как уже говорилось, соответствует распределённому термину, а неполный – нераспределённому. Например, требуется установить распределённость терминов в суждении: «
Некоторые русские писатели – это всемирно известные люди». Сначала найдём в этом суждении субъект и предикат: «
русские писатели» – субъект, «
всемирно известные люди» – предикат. Теперь установим, в каком они отношении. Русский писатель может как быть, так и не быть всемирно известным человеком, и всемирно известный человек может как быть, так и не быть русским писателем, следовательно, субъект и предикат указанного суждения находятся в отношении пересечения. Изобразим это отношение на схеме Эйлера, заштриховав ту часть, о которой идёт речь в суждении (рис. 25):
И субъект, и предикат изображаются неполными кругами (у каждого из них как бы отрезана какая-то часть), следовательно, оба термина предложенного суждения нераспределены (
S–,
P–).
Рассмотрим ещё один пример. Надо установить распределённость терминов в суждении: «
Некоторые люди – это спортсмены». Найдя в этом суждении субъект и предикат: «
люди» – субъект, «
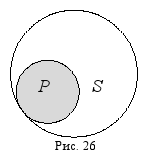
спортсмены» – предикат, и установив отношение между ними – подчинение, изобразим его на схеме Эйлера, заштриховав ту часть, о которой идёт речь в суждении (рис. 26):
Круг, обозначающий предикат, является полным, а круг, соответствующий субъекту, – неполным (круг предиката как бы вырезает из него какую-то часть). Таким образом, в данном суждении субъект нераспределён, а предикат распределён (
S–,
P–).
Проверьте себя:
1. В каком случае термин суждения считается распределённым, а в каком – нераспределённым? Как с помощью круговых схем Эйлера можно установить распределённость терминов в простом суждении?
2. Какова распределённость терминов во всех видах простых суждений и во всех случаях отношений между их субъектом и предикатом?
3. С помощью схем Эйлера установите распределённость терминов в следующих суждениях:
1)
Все насекомые являются живыми организмами. 2)
Некоторые книги – это учебники. 3)
Некоторые учащиеся не являются успевающими. 4)
Все города – это населённые пункты. 5)
Ни одна рыба не является млекопитающим. 6)
Некоторые древние греки являются знаменитыми учёными. 7)
Некоторые небесные тела – это звёзды. 8)
Все ромбы с прямыми углами – это квадраты.
2.4. Преобразование простого суждения
Существует три способа преобразования, т. е. изменения формы, простых суждений: обращение, превращение и противопоставление предикату.
Обращение(
конверсия) – это преобразование простого суждения, при котором субъект и предикат меняются местами. Например, суждение: «
Все акулы являются рыбами», – преобразуется путём обращения в суждение: «
Некоторые рыбы являются акулами». Здесь может возникнуть вопрос, почему исходное суждение начинается с квантора «
все», а новое – с квантора «
некоторые»? Этот вопрос, на первый взгляд, кажется странным, ведь нельзя же сказать: «
Все рыбы являются акулами», – следовательно, единственное, что остаётся, это: «
Некоторые рыбы являются акулами». Однако в данном случае, мы обратились к содержанию суждения и по смыслу поменяли квантор «
все» на квантор «
некоторые»; а логика, как уже говорилось, отвлекается от содержания мышления и занимается только его формой. Поэтому обращение суждения: «
Все акулы являются рыбами», – можно выполнить формально, не обращаясь к его содержанию (смыслу). Для этого установим распределённость терминов в этом суждении с помощью круговой схемы. Термины суждения, т. е. субъект «
акулы» и предикат «
рыбы», находятся в данном случае в отношении подчинения (рис. 27):
На круговой схеме видно, что субъект распределён (полный круг), а предикат нераспределён (неполный круг). Вспомнив, что термин распределён, когда речь идёт обо всех входящих в него предметах, и нераспределён, когда – не обо всех, мы автоматически мысленно ставим перед термином «
акулы» квантор «
все», а перед термином «
рыбы» квантор «
некоторые». Делая обращение указанного суждения, т. е. меняя местами его субъект и предикат и начиная новое суждение с термина «
рыбы», мы опять же автоматически снабжаем его квантором «
некоторые», не задумываясь о содержании исходного и нового суждений, и получаем безошибочный вариант: «
Некоторые рыбы являются акулами». Возможно, всё это покажется чрезмерным усложнением элементарной операции, однако, как увидим далее, в иных случаях преобразование суждений сделать непросто без использования распределённости терминов и круговых схем.
Обратим внимание на то, что в рассмотренном выше примере исходное суждение было вида
A, а новое – вида
I, т. е. операция обращения привела к смене вида простого суждения. При этом, конечно же, поменялась его форма, но не поменялось содержание, ведь в суждениях: «
Все акулы являются рыбами» и «
Некоторые рыбы являются акулами», – речь идёт об одном и том же. В табл. 5 представлены все случаи обращения в зависимости от вида простого суждения и характера отношений между его субъектом и предикатом:
Суждение вида
Aобращается или в само себя, или в суждение вида
I. Суждение вида
Iобращается или в само себя, или в суждение вида
A. Суждение вида
Eвсегда обращается в само себя, а суждение вида
Oне поддаётся обращению.
Второй способ преобразования простых суждений, называемый
превращением(
обверсией), заключается в том, что у суждения меняется связка: положительная на отрицательную, или наоборот. При этом предикат суждения заменяется противоречащим понятием (т. е. перед предикатом ставится частица «не»). Например, то же самое суждение, которое мы рассматривали в качестве примера для обращения: «
Все акулы являются рыбами», – преобразуется путём превращения в суждение: «
Все акулы не являются не рыбами». Это суждение может показаться странным, ведь обычно так не говорят, хотя на самом деле перед нами более короткая формулировка той мысли, что ни одна акула не может быть таким существом, которое не является рыбой, или что множество всех акул исключается из множества всех существ, которые не являются рыбами. Субъект «
акулы» и предикат «
не рыбы» суждения, получившегося в результате превращения, находятся в отношении несовместимости.
Приведённый пример превращения демонстрирует важную логическую закономерность: любое утверждение равно двойному отрицанию, и наоборот. Как видим, исходное суждение вида
Aв результате превращения стало суждением вида
E. В отличие от обращения превращение не зависит от характера отношений между субъектом и предикатом простого суждения. Поэтому суждение вида
Aвсегда превращается в суждение вида
E, а суждение вида
E– в суждение вида
A. Суждение вида
Iвсегда превращается в суждение вида
O, а суждение вида
O– в суждение вида
I(рис. 28).
Третий способ преобразования простых суждений –
противопоставление предикату– состоит в том, что сначала суждение подвергается превращению, а потом обращению. Например, чтобы путём противопоставления предикату преобразовать суждение: «
Все акулы являются рыбами», – надо сначала подвергнуть его превращению. Получится: «
Все акулы не являются не рыбами». Теперь надо совершить обращение с получившимся суждением, т. е. поменять местами его субъект «
акулы» и предикат «
не рыбы». Чтобы не ошибиться, вновь прибегнем к установлению распределённости терминов с помощью круговой схемы (субъект и предикат в этом суждении находятся в отношении несовместимости) (рис. 29):
На круговой схеме видно, что и субъект, и предикат распределены (и тому, и другому термину соответствует полный круг), следовательно, мы должны сопроводить как субъект, так и предикат квантором «
все». После этого совершим обращение с суждением: «
Все акулы не являются не рыбами». Получится: «
Все не рыбы не являются акулами». Суждение звучит непривычно, однако это – более короткая формулировка той мысли, что если какое-то существо не является рыбой, то оно никак не может быть акулой, или что все существа, которые не являются рыбами, автоматически не могут быть и акулами в том числе. Обращение можно было сделать и проще, посмотрев в табл. 5 для обращения, которая приведена выше. Увидев, что суждение вида
Eвсегда обращается в само себя, мы могли, не используя круговой схемы и не устанавливая распределённости терминов, сразу поставить перед предикатом «
не рыбы» квантор «
все». В данном случае был предложен другой способ, чтобы показать, что вполне можно обойтись без табл. для обращения, и запоминать её совсем необязательно. Здесь происходит примерно то же самое, что и в математике: можно запоминать различные формулы, но можно обойтись и без запоминания, т. к. любую формулу нетрудно вывести самостоятельно.
Все три операции преобразования простых суждений проще всего совершать с помощью круговых схем. Для этого надо изобразить три термина: субъект, предикат и понятие, противоречащее предикату (непредикат). Потом следует установить их распределённость, и из получившейся схемы Эйлера будут вытекать четыре суждения – одно исходное и три результата преобразований. Главное, помнить, что распределённый термин соответствует квантору «
все», а нераспределённый – квантору «
некоторые»; что соприкасающиеся на схеме Эйлера круги соответствуют связке «
является», а несоприкасающиеся – связке «
не является». Например, требуется совершить три операции преобразования с суждением: «
Все учебники являются книгами». Изобразим субъект «
учебники», предикат «
книги» и непредикат «
не книги» круговой схемой и установим распределённость этих терминов (рис. 30):
Получившуюся круговую схему можно прочитать четырьмя способами:
1.
Все учебники являются книгами(исходное суждение).
2.
Некоторые книги являются учебниками(обращение).
3.
Все учебники не являются не книгами(превращение).
4.
Все не книги не являются учебниками(противопоставление предикату).
Рассмотрим ещё один пример. Надо преобразовать тремя способами суждение: «
Все планеты не являются звёздами». Изобразим кругами Эйлера субъект «
планеты», предикат «
звёзды» и непредикат «
не звёзды». Обратите внимание на то, что понятия «
планеты» и «
не звёзды» находятся в отношении подчинения: планета – это обязательно не звезда, но небесное тело, которое не является звездой – это не обязательно планета. Установим распределённость этих терминов (рис. 31):
Получившуюся круговую схему можно прочитать четырьмя разными способами:
1.
Все планеты не являются звёздами(исходное суждение).
2.
Все звёзды не являются планетами(обращение).
3.
Все планеты являются не звёздами(превращение).
4.
Некоторые не звёзды являются планетами(противопоставление предикату).
Проверьте себя:
1. Каким образом осуществляется операция обращения? Возьмите три каких-нибудь суждения и произведите с каждым из них обращение. Как происходит обращение во всех видах простых суждений и во всех случаях отношений между их субъектом и предикатом? Какие суждения не поддаются обращению?
2. Что такое превращение? Возьмите три любых суждения и совершите с каждым из них операцию превращения.
3. Что представляет собой операция противопоставления предикату? Возьмите три каких-нибудь суждения и преобразуйте каждое из них путём противопоставления предикату.
4. Каким образом знания о распределённости терминов в простых суждениях и умение её устанавливать с помощью круговых схем может помочь в проведении операций преобразования суждений?
5. Возьмите какое-нибудь суждение вида
Aи совершите с ним все операции преобразования с помощью круговых схем и установления распределённости терминов. Сделайте то же самое с каким-нибудь суждением вида
E.
2.5. Логический квадрат
Простые суждения делятся на сравнимые и несравнимые.
Сравнимые (идентичные по материалу)суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками. Например, суждения: «
Все школьники изучают математику», «
Некоторые школьники не изучают математику», – являются сравнимыми: у них совпадают субъекты и предикаты, а кванторы и связки различаются.
Несравнимыесуждения имеют разные субъекты и предикаты. Например, суждения: «
Все школьники изучают математику», «
Некоторые спортсмены – это олимпийские чемпионы», – являются несравнимыми: субъекты и предикаты у них не совпадают.
Сравнимые суждения бывают, как и понятия, совместимыми и несовместимыми и могут находиться в различных отношениях между собой.
Совместимыминазываются суждения, которые могут быть одновременно истинными. Например, суждения: «
Некоторые люди – это спортсмены», «
Некоторые люди – это не спортсмены», – являются одновременно истинными и представляют собой совместимые суждения.
Несовместимыминазываются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например, суждения: «
Все школьники изучают математику», «Некоторые школьники не изучают математику», – не могут быть одновременно истинными и являются несовместимыми (истинность первого суждения с неизбежностью приводит к ложности второго).
Совместимые суждения могут находиться в следующих отношениях:
1.
Равнозначность– это отношение между двумя суждениями, у которых и субъекты, и предикаты, и связки, и кванторы совпадают. Например, суждения: «
Москва является древним городом»,
«
Столица России является древним городом», – находятся в отношении равнозначности.
2.
Подчинение– это отношение между двумя суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении вида и рода. Например, суждения: «
Все растения являются живыми организмами», «
Все цветы (некоторые растения) являются живыми организмами», – находятся в отношении подчинения.
3.
Частичное совпадение
(субконтрарность)– это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: «
Некоторые грибы являются съедобными», «
Некоторые грибы не являются съедобными», – находятся в отношении частичного совпадения. Необходимо отметить, что в этом отношении находятся только частные суждения – частноутвердительные (
I) и частноотрицательные (
O).
Несовместимые суждения могут находиться в следующих отношениях.
1.
Противоположность
(контрарность)– это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: «
Все люди являются правдивыми», «
Все люди не являются правдивыми», – находятся в отношении противоположности. В этом отношении могут быть только общие суждения – общеутвердительные (
A) и общеотрицательные (
E). Важным признаком противоположных суждений является то, что они не могут быть одновременно истинными, но могут быть одновременно ложными. Так, два приведённых противоположных суждения не могут быть одновременно истинными, но могут быть одновременно ложными: неправда, что все люди являются правдивыми, но также неправда, что все люди не являются правдивыми.
Противоположные суждения могут быть одновременно ложными, потому что между ними, обозначающими какие-то крайние варианты, всегда есть третий, средний, промежуточный вариант. Если этот средний вариант будет истинным, то два крайних окажутся ложными. Между противоположными (крайними) суждениями: «
Все люди являются правдивыми», «
Все люди не являются правдивыми», – есть третий, средний вариант: «
Некоторые люди являются правдивыми, а некоторые не являются таковыми», – который, будучи истинным суждением, обусловливает одновременную ложность двух крайних, противоположных суждений.
2.
Противоречие
(контрадикторность)– это отношение между двумя суждениями, у которых предикаты совпадают, связки различны, а субъекты отличаются своими объёмами, т. е. находятся в отношении подчинения (вида и рода). Например, суждения: «
Все люди являются правдивыми», «Некоторые люди не являются правдивыми», – находятся в отношении противоречия. Важным признаком противоречащих суждений, в отличие от противоположных, является то, что между ними не может быть третьего, среднего, промежуточного варианта. В силу этого два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них обязательно означает ложность другого, и наоборот – ложность одного обусловливает истинность другого. К противоположным и противоречащим суждениям мы ещё вернёмся, когда речь пойдёт о логических законах противоречия и исключённого третьего.
Рассмотренные отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата (рис. 32), который был разработан ещё средневековыми логиками:
Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так, суждения вида
Aи вида
I, а также суждения вида
Eи вида
Oнаходятся в отношении подчинения. Суждения вида
Aи вида
Eнаходятся в отношении противоположности, а суждения вида
Iи вида
O– частичного совпадения. Суждения вида
Aи вида
O, а также суждения вида
Eи вида
Iнаходятся в отношении противоречия. Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями
Aи
A,
Iи
I,
Eи
E,
Oи
O. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: «
Все люди изучали логику», «
Некоторые люди не изучали логику». Видя, что первое суждение является общеутвердительным (
A), а второе частноотрицательным (
O), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Суждения: «
Все люди изучали логику (A)», «
Некоторые люди изучали логику (I)», находятся в отношении подчинения, а суждения: «
Все люди изучали логику (A)», «
Все люди не изучали логику (E)», – находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными.
Что касается сравнимых суждений, то истинностные значения каждого из них определённым образом связаны с истинностными значениями остальных. Так, если суждение вида
Aявляется истинным или ложным, то три других (
I,
E,
O), сравнимых с ним суждения (имеющих сходные с ним субъекты и предикаты), в зависимости от этого (от истинности или ложности суждения вида
A) тоже являются истинными или ложными. Например, если суждение вида
A: «
Все тигры – это хищники», – является истинным, то суждение вида
I: «
Некоторые тигры – это хищники», – также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида
E: «
Все тигры – это не хищники», – является ложным, и суждение вида
O: «
Некоторые тигры – это не хищники», – также является ложным. Таким образом, в данном случае из истинности суждения вида
Aвытекает истинность суждения вида
Iи ложность суждений вида
Eи вида
O(разумеется, речь идёт о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
Проверьте себя:
1. Какие суждения называются сравнимыми и какие – несравнимыми?
2. Что такое совместимые и несовместимые суждения? Приведите по три примера совместимых и несовместимых суждений.
3. В каких отношениях могут быть совместимые суждения? Приведите по два примера для отношений равнозначности, подчинения и частичного совпадения.
4. В каких отношениях могут быть несовместимые суждения?
Приведите по три примера для отношений противоположности и противоречия. Почему противоположные суждения могут быть одновременно ложными, а противоречащие не могут?
5. Что представляет собой логический квадрат? Каким образом он изображает отношения между суждениями? Почему логический квадрат не изображает отношение равнозначности? Как с помощью логического квадрата определять отношение между двумя простыми сравнимыми суждениями?
6. Возьмите какое-нибудь истинное или ложное суждения вида
Aи сделайте из него выводы об истинности сравнимых с ним суждений видов
E,
I,
O. Возьмите какое-нибудь истинное или ложное суждения вида
Eи сделайте из него выводы об истинности сравнимых с ним суждений
A,
I,
O.
2.6. Сложное суждение
В зависимости от союза, с помощью которого простые суждения соединяются в сложные, выделяется пять видов сложных суждений:
1.
Конъюнктивное суждение (конъюнкция)– это сложное суждение с соединительным союзом «и», который обозначается в логике условным знаком «?». С помощью этого знака конъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a?
b(читается «
aи
b»), где
aи
b– это два каких-либо простых суждения. Например, сложное суждение: «
Сверкнула молния, и загремел гром», – является конъюнкцией (соединением) двух простых суждений:
«Сверкнула молния», «Загремел гром». Конъюнкция может состоять не только из двух, но и из большего числа простых суждений. Например: «
Сверкнула молния, и загремел гром, и пошёл дождь(
a?
b?
c)».
2.
Дизъюнктивное суждение
(дизъюнкция)– это сложное суждение с разделительным союзом «или». Вспомним, что, говоря о логических операциях сложения и умножения понятий, мы отмечали неоднозначность этого союза – он может использоваться как в нестрогом (неисключающем) значении, так и в строгом (исключающем). Неудивительно поэтому, что дизъюнктивные суждения делятся на два вида:
1. Нестрогая дизъюнкция– это сложное суждение с разделительным союзом «или» в его нестрогом (неисключающем) значении, который обозначается условным знаком «?». С помощью этого знака нестрогое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a?
b(читается «
aили
b»), где
aи
b– это два простых суждения. Например, сложное суждение: «
Он изучает английский, или он изучает немецкий», – является нестрогой дизъюнкцией (разделением) двух простых суждений:
«Он изучает английский», «Он изучает немецкий».Эти суждения друг друга не исключают, ведь возможно изучать и английский, и немецкий одновременно, поэтому данная дизъюнкция является нестрогой.
2. Строгая дизъюнкция– это сложное суждение с разделительным союзом «или» в его строгом (исключающем) значении, который обозначается условным знаком «
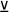
». С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a
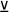 b
b(читается «или
a, или
b»), где
aи
b– это два простых суждения. Например, сложное суждение: «
Он учится в 9 классе, или он учится в 11 классе», – является строгой дизъюнкцией (разделением) двух простых суждений:
«Он учится в 9 классе», «Он учится в 11 классе». Обратим внимание на то, что эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9, и в 11 классе (если он учится в 9 классе, то точно не учится в 11 классе, и наоборот), в силу чего данная дизъюнкция является строгой.
Как нестрогая, так и строгая дизъюнкции могут состоять не только из двух, но и из большего числа простых суждений. Например: «
Он изучает английский, или он изучает немецкий, или он изучает французский (a ? b ? c)», «
Он учится в 9 классе, или он учится в 10 классе, или он учится в 11 классе (a
b
c)».
3.
Импликативное суждение
(импликация)– это сложное суждение с условным союзом «если … то», который обозначается условным знаком «?». С помощью этого знака импликативное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a?
b(читается «если
a, то
b»), где
aи
b– это два простых суждения. Например, сложное суждение: «
Если вещество является металлом, то оно электропроводно», – представляет собой импликативное суждение (причинно-следственную связь) двух простых суждений:
«Вещество является металлом», «Вещество электропроводно». В данном случае эти два суждения связаны таким образом, что из первого вытекает второе (если вещество – металл, то оно обязательно электропроводно), однако из второго не вытекает первое (если вещество электропроводно, то это вовсе не означает, что оно является металлом). Первая часть импликации называется
основанием, а вторая –
следствием; из основания вытекает следствие, но из следствия не вытекает основание. Формулу импликации:
a?
b, можно прочитать так: «если
a, то обязательно
b, но если
b, то не обязательно
a».
4.
Эквивалентное суждение
(эквиваленция)– это сложное суждение с союзом «если … то» не в его условном значении (как в случае с импликацией), а в тождественном (эквивалентном).


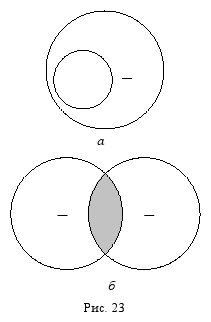
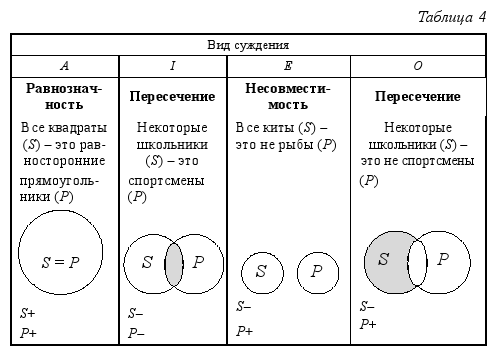


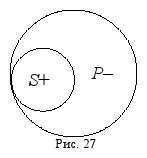

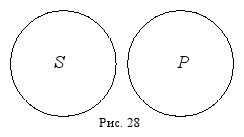
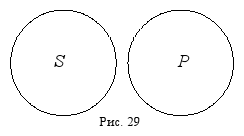



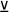 ». С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a
». С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы:
a