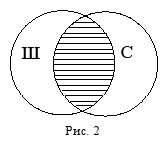В логике отношения между понятиями принято изображать с помощью круговых схем Эйлера (Леонард Эйлер – известный математик XVIII в.): одно понятие, а вернее его объём, изображается одним кругом, а второе, т. е. его объём, – другим. Взаимное расположение этих кругов на схеме (они могут полностью совпадать, или пересекаться, или не соприкасаться, или один круг может располагаться внутри другого) и показывает то или иное отношение между понятиями. Так, отношение равнозначности между понятиями «
квадрат» (К) и «
равносторонний прямоугольник» (Р. п.) изображается схемой, на которой два круга, обозначающие два равных объёма, полностью совпадают (рис. 1).
Понятия находятся в отношении
пересечениятогда, когда их объёмы совпадают только частично. Например, пересекающимися будут понятия «
школьник» (Ш) и «
спортсмен» (С): есть такие школьники, которые являются спортсменами, и есть такие спортсмены, которые являются школьниками; но в то же время школьник может не быть спортсменом, так же как и спортсмен может не быть школьником. На схеме Эйлера отношение пересечения изображается двумя пересекающимися кругами (заштрихованная часть показывает частично совпадающие объёмы двух понятий)
Понятия находятся в отношении
подчиненияв том случае, когда объём одного из них обязательно больше объёма другого и полностью его в себя включает (один объём как бы подчиняется другому). Например, в отношении подчинения находятся понятия «
карась» (К) и «
рыба» (Р), т. к. все караси – это обязательно рыбы, но рыбами являются не только караси, есть и другие виды рыб. Таким образом, объём понятия «
карась» является меньшим по отношению к объёму понятия «
рыба» и полностью в него включается (подчиняется ему). В отношении подчинения понятия с меньшим объёмом называются
видовыми, а с большим –
родовыми. На схеме Эйлера отношение подчинения изображается двумя кругами, один из которых располагается внутри другого (рис. 3).
Отношениями равнозначности, пересечения и подчинения исчерпываются все случаи совместимости между понятиями.
Несовместимые понятия могут быть в отношениях соподчинения, противоположности и противоречия.
Понятия находятся в отношении
соподчинениятогда, когда их объёмы не имеют общих элементов, но в то же время входят в объём какого-то третьего понятия, родового для них (совместно ему подчиняются). Например, понятия «
сосна» (С) и «
берёза» (Б) являются соподчинёнными: ни одна сосна не может быть берёзой, и наоборот, но и множество всех сосен, и множество всех берёз включается в более широкий объём понятия «
дерево» (Д). На схеме Эйлера отношение соподчинения изображается двумя несоприкасающимися кругами (рис. 4).
Понятия находятся в отношении
противоположностив том случае, если они обозначают какие-то взаимоисключающие признаки, крайние состояния чего-либо, между которыми, однако, всегда есть некий средний, переходный вариант. Например, противоположными являются понятия «
высокий человек» (В. ч.) и «
низкий человек» (Н. ч.) Третьим (переходным) вариантом между ними будет понятие «
человек среднего роста». На схеме Эйлера отношение противоположности изображается двумя несоприкасающимися кругами, которые находятся как бы на разных полюсах (рис. 5).
Поскольку объёмы противоположных понятий не соприкасаются, это отношение отчасти похоже на соподчинение. Однако понятия, находящиеся в отношении соподчинения, обозначают просто различные объекты разных видов и одного рода, но не противоположные друг другу. Не можем же мы утверждать, что сосна является противоположностью берёзы, а берёза – противоположностью сосны: это просто разные деревья, и не более того. В то же время высокий человек представляет собой противоположность низкого человека и наоборот. Так же противоположными будут понятия «
тёмная комната» и «
светлая комната», «
горячая вода» и «
холодная вода», «
белый лист» и «
чёрный лист», «
глубокая речка» и «
мелкая речка» и т. п.
Понятия находятся в отношении
противоречия, если одно из них представляет собой отрицание другого, причём в отличие от противоположных понятий, между противоречащими понятиями не может быть третьего (среднего) варианта. Например, в отношении противоречия находятся понятия «
высокий человек» (В. ч.) и «
невысокий человек» (Нв. ч.). В том случае, когда одно понятие является отрицанием другого, третий вариант автоматически исключается: и низкий человек, и человек среднего роста – это невысокий человек. На схеме Эйлера отношение противоречия изображается одним кругом, поделённым на две части, которые обозначают противоречащие понятия (рис. 6).
Отношениями соподчинения, противоположности и противоречия исчерпываются все случаи несовместимости между понятиями.
Итак, в логике выделяется шесть вариантов отношений между понятиями. Для удобства их запоминания они представлены в табл. 2.
Любые два сравнимых понятия обязательно находятся в одном из шести указанных случаев отношений. Например, понятия «
писатель» и «
россиянин» находятся в отношении пересечения, «
писатель» и «
человек» – подчинения, «
Москва» и «
столица России» – равнозначности, «
Москва» и «
Санкт-Петербург» – соподчинения, «
мокрая дорога» и «
сухая дорога» – противоположности, «
Антарктида» и «
материк» – подчинения, «
Антарктида» и «
Африка» – соподчинения и т. д. Надо обратить внимание на то, что если два понятия обозначают часть и целое, например «
месяц» и «
год», то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год.
Однако если бы понятия «
месяц» и «
год» были подчинёнными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий «
карась» и «
рыба»: карась – это обязательно рыба, но рыба – это не обязательно карась). Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия «
месяц» и «
год», так же, как и понятия «
книга» и «
страница книги», «
автомобиль» и «
колесо автомобиля», «
молекула» и «
атом», находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.
Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причём до сих пор мы изображали схематично отношения между двумя понятиями, но это можно сделать и с большим числом понятий.
Например, отношения между понятиями «
боксёр» (Б), «
негр» (Н) и «
человек» (Ч) изображаются следующей схемой Эйлера (рис. 7).
Взаимное расположение кругов показывает, что понятия «
боксёр» и «
негр» находятся в отношении пересечения: боксёр может быть негром и может им не быть, а негр также может быть боксёром и может им не быть, а понятия «
боксёр» и «
человек», так же как понятия «
негр» и «
человек», находятся в отношении подчинения: любой боксёр и любой негр – это обязательно человек, но человек может не быть ни боксёром, ни негром.
Рассмотрим отношения между понятиями «
дедушка» (Д), «
отец» (О), «
мужчина» (М), «
человек» (Ч) с помощью схемы Эйлера (рис. 8).
Указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина.
Отношения между понятиями «
хищник» (Х), «
рыба» (Р), «
акула» (А), «
пиранья» (П), «
щука» (Щ), «
живое существо» изображаются следующей схемой Эйлера (рис. 9).
Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.
Подытоживая всё сказанное, отметим, что отношения между понятиями – это отношения между их объёмами. Значит, для того чтобы можно было установить отношения между понятиями, их объём должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определёнными.
Проверьте себя:
1. Какие понятия называются в логике совместимыми, а какие – несовместимыми? Приведите по пять примеров совместимых и несовместимых понятий.
2. В каких отношениях могут быть совместимые понятия? Что представляют собой отношения равнозначности, пересечения и подчинения между понятиями? Что такое видовые и родовые понятия?
3. В каких отношениях могут быть несовместимые понятия? Что представляют собой отношения соподчинения, противоположности и противоречия между понятиями? Чем отличается противоположность от соподчинения и противоречие от противоположности?
4. Каким образом изображаются отношения между понятиями?
5. В каком отношении находятся понятия, обозначающие часть и целое? Почему между этими понятиями не может быть отношения подчинения?
6. Определите, в каких отношениях находятся следующие понятия:
двоечники
студент,
композитори
человек,
городи
деревня,
Антарктидаи
ледовый материк,
небесное телои
звезда,
треугольники
сторона треугольника,
школа №5и
учебное заведение,
майори
россиянин,
знаменитый человеки
немецкий писатель,
доми
крыша дома,
собакаи
кошка,
умный человеки
неумный человек,
монархи
самодержец,
физикаи
химия,
геометрияи
тригонометрия,
столицаи
населённый пункт,
книгаи
интересная книга,
телевизори
планета солнечной системы,
растениеи
крапива,
окружностьи
круг,
Николай IIи
последний русский царь,
олимпийские игрыи
спортивные состязания.
1.4. Ограничение и обобщение понятия
Видовые и родовые понятия тесно связаны между собой логическими операциями ограничения и обобщения.
Ограничение понятия– это логическая операция перехода от родового понятия к видовому с помощью прибавления к его содержанию какого-либо признака (или нескольких признаков).
Вспомним об обратном отношении между объёмом и содержанием понятия: чем больше объём, тем меньше содержание, и наоборот. Ограничение понятия, или переход от родового понятия к видовому – это уменьшение его объёма, а значит – увеличение содержания. Вот почему при добавлении каких-либо признаков к содержанию понятия автоматически уменьшается его объём. Например, если к содержанию понятия «
физический прибор» (Ф. п.) прибавить признак «
измерять напряжение электрического тока», то оно превратится в понятие «
вольтметр» (В), которое будет видовым по отношению к исходному родовому понятию «
физический прибор» (рис. 10).
Так же, если к содержанию понятия «
геометрическая фигура» (Г. ф.) прибавить признак «
иметь равные стороны и прямые углы», то оно превратится в понятие «
квадрат» (К), которое будет видовым по отношению к исходному родовому понятию «
геометрическая фигура» (рис. 11).
Обобщение понятия– это логическая операция перехода от видового понятия к родовому с помощью исключения из его содержания какого-либо признака (или нескольких признаков). Содержание понятия, лишённое каких-то признаков, уменьшается, но при этом автоматически увеличивается объём понятия, которое из видового становится родовым или обобщается. Например, если от содержания понятия «
биология» (Б) отбросить признак «
изучать различные формы жизни», то оно превратится в понятие «
наука» (Н), которое будет родовым по отношению к исходному видовому понятию «
биология» (рис. 12).
Так же, если от содержания понятия «
атом водорода» (А. в.) отбросить признак «
иметь один электрон», то оно превратится в понятие «
атом химического элемента» (А. х. э.), которое будет родовым по отношению к исходному видовому понятию «
атом водорода» (рис. 13).
Ограничения и обобщения понятий складываются в логические цепочки, в которых каждое понятие (за исключением начального и конечного) является видовым по отношению к одному соседнему понятию и родовым по отношению к другому. Например, если последовательно обобщать понятие «
Солнце», то получится следующая цепочка:
Солнце?
звезда?
небесное тело? ?
физическое тело?
форма материи. В этой цепочке понятие «
звезда» является родовым по отношению к понятию «
Солнце», но видовым по отношению к понятию «
небесное тело»; так же понятие «
небесное тело» является родовым по отношению к понятию «
звезда», но видовым по отношению к понятию «
физическое тело» и т. д. Движение по нашей цепочке от понятия «Солнце» к понятию «
форма материи» представляет собой серию последовательных обобщений, а движение в обратном направлении – серию ограничений. Если изобразить отношения между понятиями из указанной цепочки на схеме Эйлера, то получатся круги, последовательно располагающиеся один в другом: самый маленький будет обозначать понятие «
Солнце», а самый большой – «
форма материи».
Пределом цепочки ограничения любого понятия всегда будет какое-либо единичное понятие (см. раздел 1.1.), а пределом цепочки обобщения, как правило, будет какое-либо широкое, философское понятие, например:
объект мироздания, форма материиили
форма бытия.
Наиболее частые ошибки, которые допускают при ограничении и обобщении понятий, заключаются в том, что вместо вида для какого-то рода называют часть из некого целого, и вместо рода для какого-то вида называют целое по отношению к какой-либо части. Например, в качестве ограничения понятия «
цветок» предлагают понятие «
стебель». Действительно, стебель – это часть цветка, но ограничить понятие – значит подобрать не часть для целого, а вид для рода. Следовательно, правильным ограничением понятия «
цветок» будет понятие «
ромашка», или «
тюльпан», или «
хризантема» и т. п. В качестве обобщения понятия «
дерево» нередко предлагают понятие «
лес». Конечно же, лес является неким целым по отношению к деревьям, из которых он состоит, но обобщить понятие – значит подобрать не целое для части, а род для вида. Следовательно, правильным обобщением понятия «
дерево» будет понятие «
растение», или «
объект флоры», или «
живой организм» и т. п.
Итак, почти любое понятие (за исключением единичных и широких, философских) можно как ограничить, так и обобщить. Другими словами, подобрать для него как видовое понятие, так и родовое. Например, ограничением понятия «
человек» (Ч) будет понятие «
спортсмен» (С) или «
писатель», или «
мужчина», или «
молодой человек» и т. п., а его обобщением будет понятие «
живое существо» (Ж. с.) (рис. 14).
Проверьте себя:
1. Что такое ограничение понятия?
2. Что представляет собой логическая операция обобщения понятия?
3. Каким образом ограничения и обобщения понятий складываются в логические цепочки? Каковы пределы цепочек ограничений и обобщений?
4. Какие ошибки часто допускают при ограничении и обобщении понятий? Продемонстрируйте на самостоятельно подобранных примерах, что целое и часть нельзя путать с видом и родом.
5. Всякое ли понятие можно подвергнуть ограничению или обобщению? Какие понятия не поддаются этим логическим операциям?
6. Подберите десять любых понятий и проделайте с ними ограничение и обобщение, т. е. подберите для каждого как видовое, так и родовое понятие, иллюстрируя эти операции схемами Эйлера.
1.5. Операция определения понятия
Определение понятия– это логическая операция, которая раскрывает содержание понятия.
Определения бывают явными и неявными.
Явноеопределение непосредственно раскрывает содержание понятия, даёт прямой ответ на вопрос, чем является объект, который оно обозначает. Например: «
Термометр – это физический прибор, предназначенный для измерения температуры», – явное определение.
Неявное
(контекстуальное)определение раскрывает содержание понятия не прямо, а косвенно, с помощью контекста, в котором это понятие употребляется. Например, из следующей фразы: «
Во время этого грандиозного эксперимента сверхточные термометры зафиксировали температуру в 1 000 °C», – косвенно следует ответ на вопрос: «Что такое термометр?» – вытекает неявное определение этого понятия. Понятно, что определениями в полном смысле этого слова надо считать явные определения. В дальнейшем речь пойдёт именно о них.
Определения также бывают реальными и номинальными.
Реальноеопределение раскрывает содержание понятия, обозначающего какой-то объект, т. е. они посвящены объектам. Например:
«
Термометр – это физический прибор, предназначенный для измерения температуры» – реальное определение.
Номинальное(от лат. nomen – имя) раскрывает значение термина, которым выражено какое-либо понятие, т. е они посвящены терминам (словам). Например: «
Слово «термометр» обозначает физический прибор, предназначенный для измерения температуры», – номинальное определение.
Как видим, принципиальной разницы между реальными и номинальными определениями не существует. Они различаются, как правило, по форме, но не по сути.
Существует несколько способов определения понятия, но среди них выделяется классический способ, который заключается в том, что определяемое понятие подводится под ближайшее к нему родовое понятие, после чего следует указание на его видовое отличие. Например, определение: «
Астрономия – это наука о небесных телах», – построено по классическому способу. В нём определяемое понятие «
астрономия» сначала подводится под ближайшее к нему родовое понятие «
наука» (астрономия – это обязательно наука, но наука – это не обязательно астрономия), а потом указывается на видовое отличие астрономии от других наук: «…
о небесных телах». Пользуясь классическим способом, вы сможете дать точное и правильное определение любому понятию, конечно, если определяемый объект или термин вам хорошо знаком, и вы знаете, что он собой представляет или что означает, соответственно. Например, нам требуется дать определение понятию «
квадрат». Следуя классическому способу, сначала подведём его под родовое понятие: «
Квадрат – это геометрическая фигура», – а затем укажем его видовое отличие от других геометрических фигур, которое заключается в наличии
равных сторон и прямых углов. Итак: «
Квадрат – это геометрическая фигура, у которой все стороны равны и углы прямые». Давая определение понятию «
квадрат», мы могли бы подвести его под более близкое родовое понятие «
прямоугольник», и тогда определение получилось бы следующим: «
Квадрат – это прямоугольник, у которого все стороны равны», – однако и приведённое выше определение квадрата раскрывает содержание соответствующего понятия и является верным. Обратите внимание на то, что фактически все определения, встречающиеся в научной, учебной и справочной литературе, например в толковых словарях, построены по классическому способу.
Существует несколько логических правил определения. Нарушение хотя бы одного из них приводит к тому, что содержание понятия не раскрывается и определение не достигает своей цели, являясь неверным. Рассмотрим эти правила и ошибки, возникающие при их нарушении:
1.
Определение не должно быть широким, т. е. определение не должно превышать своим объёмом определяемое понятие. Например, определение: «
Солнце – это небесное тело», – является
широким: определение «
небесное тело» по объёму намного больше определяемого понятия «
Солнце». Из приведённого определения не вполне понятно, что такое Солнце, ведь небесное тело – это и планета, и комета и т. п. В данном случае можно также сказать, что, пользуясь классическим способом определения, мы подвели определяемое понятие «
Солнце» под родовое понятие «
небесное тело», но не сделали второй шаг – не указали на его видовое отличие.
2.
Определение не должно быть узким, т. е. определение не должно быть по своему объёму меньше определяемого понятия. Например, определение: «
Геометрия – это наука о треугольниках», – является
узким. Геометрия действительно наука о треугольниках, но не только о них, а в нашем примере определение получилось по объёму меньше определяемого понятия, в результате чего из приведённого определения не совсем ясно, что такое геометрия, содержание понятия не раскрывается.
Как видим, ошибка узкого определения противоположна ошибке широкого определения. Если определение не должно быть широким и не должно быть узким, то каким же тогда оно должно быть? Оно должно быть соразмерным, т. е. понятие и его определение должны быть равны друг другу. Вернёмся к определению: «
Астрономия – это наука о небесных телах», – которое является соразмерным. В этом примере определяемое понятие «
астрономия» и определение: «…
наука о небесных телах» находятся в отношении равнозначности: астрономия – это именно наука о небесных телах, а наука о небесных телах – это только астрономия. Определение является соразмерным тогда, когда между его первой частью (определяемым понятием) и второй (определением) можно поставить знак « = ». Если же между первой и второй частью определения ставится знак « > » или « < », то оно является ошибочным – широким или узким соответственно. В данном случае мы видим проявление одного из основных законов логики – закона тождества.
3.
В определении не должно быть круга, т. е. в определении нельзя употреблять понятия, которые являются определяемыми. Например, в определении: «
Клеветник – это человек, который занимается клеветой», – присутствует
круг, поскольку понятие «
клеветник» определяется через понятие «
клевета», т. е. фактически – через само себя. Если бы, услышав приведённое определение, мы спросили, что такое клевета, нам могли бы ответить: «
Клевета – это то, чем занимается клеветник». Присутствующий в определении круг (или тавтология, с греч. – повтор) приводит к тому, что содержание понятия не раскрывается, и определение является ошибочным. Однако наверняка найдутся люди, которые скажут, что из определения: «
Клеветник – это человек, который занимается клеветой», – вполне понятно, и кто такой клеветник, и что такое клевета. Они могут так утверждать только потому, что им ранее было известно значение слов «
клеветник» и «
клевета». Станет ли понятно, что такое экзистенциализм из следующего кругового определения: «
Экзистенциализм – это философское направление XX в., в котором ставятся и всесторонне рассматриваются различные экзистенциальные вопросы и проблемы»? Узнаем ли мы, что такое синергетика, благодаря такому круговому определению: «
Синергетика – это раздел современного естествознания, который изучает разнообразные синергетические явления и процессы»?
4.
Определение не должно быть двусмысленным, т. е. в нём нельзя употреблять слова (термины) в переносном значении. Вспомним хорошо знакомое с детства определение: «
Лев – это царь зверей». В данном определении слово «
царь» используется в переносном значении, но у него есть и прямое значение. Получается, что в определении употребляется одно слово, а возможных значений у него два, т. е. определение является
двусмысленным(вновь нарушается логический закон тождества: одно слово, два значения: 1 ? 2).
Двусмысленность вполне уместна в качестве художественного приёма, но в определении она недопустима, поскольку содержание понятия в данном случае не раскрывается.
5.
Определение не должно быть сложным и непонятным.
Рассмотрим следующее определение: «
Энтропия – это термодинамическая функция, характеризующая часть внутренней энергии замкнутой системы, которая не может быть преобразована в механическую работу». Это определение взято не из научного доклада и не из докторской диссертации, а из учебника для студентов гуманитарных специальностей
. Данное определение не широкое и не узкое, в нём нет круга и двусмысленности, оно верно и с научной точки зрения. Это определение кажется безупречным с тем только исключением, что оно является
сложным и непонятнымдля людей, которые не занимаются специально естественными науками, т. е. для большинства из нас. Определение должно быть понятным для того, кому оно адресовано, иначе при всей своей формальной правильности оно не будет раскрывать содержания понятия для своего адресата. Непонятные определения также называют
некоммуникабельными, т. е. создающими преграды для общения между людьми.
6.
Определение не должно быть только отрицательным. Например, определение: «
Квадрат – это не треугольник», – является
только отрицательным. Квадрат – это действительно не треугольник, но данное определение не раскрывает содержание понятия «
квадрат», ведь, указав на то, чем не является объект, обозначенный определяемым понятием, мы не сказали, чем же он является (окружность, трапеция, пятиугольник – это тоже не квадраты). Определение может быть отрицательным в том случае, когда оно дополнено положительной частью. Например, определение: «
Квадрат – это не треугольник, а прямоугольник, у которого все стороны равны», – правильное.
Проверьте себя:
1. Что такое определение понятия?
2. Чем отличаются явные определения от неявных? Придумайте по три примера явных и неявных определений.
3. Что такое реальные и номинальные определения? Как вы думаете, почему любое реальное определение можно свести к номинальному, и наоборот?
4. Что представляет собой классический способ определения понятия? Дайте определения каким-нибудь трём понятиям, пользуясь классическим способом.
5. Каковы основные правила определения понятия? Какие ошибки возникают при их нарушении? Приведите, подобрав самостоятельно, по три примера для каждой ошибки в определении понятия.
6. Найдите ошибки в приведённых ниже примерах определений:
1)
Сутки – это отрезок времени, в течение которого Земля делает полный оборот вокруг своей оси.
2)
Жанр – это устойчивая форма какого-либо произведения искусства.
3)
Собака – это друг человека.
4)
Творческое мышление – это мышление, которое обеспечивает решение творческих задач.
5)
Революция – это крупное историческое событие, в результате которого в обществе меняется политическая власть.
1.6. Операция деления понятия
Деление понятия– это логическая операция, которая раскрывает его объём.
Деление понятия состоит из трёх частей: делимое понятие, результаты деления, основание деления (признак, по которому производится деление). Например, в следующем делении: «
Люди бывают мужчинами и женщинами», – или, что то же самое: «
Люди делятся на мужчин и женщин», – делимым является понятие «
люди», результаты деления – это понятия «
мужчины» и «
женщины», а основание данного деления – пол, т. к. люди в нём разделены по половому признаку. В зависимости от основания деление может быть различным. Например: «
Люди бывают высокими, низкими и среднего роста(основание деления – рост)», «
Люди бывают монголоидами, европеоидами и негроидами(основание деления – раса)», «
Люди бывают учителями, врачами, инженерами и т. д.(основание деления – профессия)». Иногда понятие делится
дихотомически(с греч. – пополам) по типу: «A и не A». Например: «
Люди бывают спортсменами и не спортсменами». Дихотомическое деление всегда правильное, т. е. в нём автоматически исключаются все возможные в делении ошибки, о которых речь пойдёт ниже.
Мы хорошо знаем, зачем нам нужна операция определения понятия: знакомство с новым предметом начинается с его определения. Теперь ответим на вопрос, какую роль в мышлении и языке выполняет операция деления понятия. Изучая разные науки, вы заметили, что ни одна из них не обходится без различных классификаций: разделений каких-то областей действительности на группы, части, виды и т. п. (классификация растений в ботанике, животных – в зоологии, химических элементов – в химии и т. д.). Однако любая классификация – это не что иное, как логическая операция деления понятия. Классификации могут быть как обширными, подробными, научными, так и простыми, обыденными, повседневными. Когда мы говорим: «
Люди делятся на мужчин и женщин» или «
Учебные заведения бывают начальными, средними и высшими», – то создаём пусть маленькую и простую, но классификацию. Итак, логическая операция деления понятия лежит в основе любой классификации, без которой не обходится ни научное, ни повседневное мышление.