Предлагаемые в этой книге задачи значительно различаются как по типу своего построения, так и по уровню сложности. Одни из них близки к математике, и для их решения надо будет составить простое уравнение, другие не имеют с ними ничего общего. Некоторые задачи предполагают знание нескольких простых законов физики, некоторые являются логическими упражнениями и головоломками, а некоторые представляют собой просто шутки, розыгрыши или фокусы. Одни задачи очень просты – вы сможете их решить за считанные секунды, а над другими, наоборот, надо изрядно поломать голову. В некоторых случаях не обойтись без карандаша и бумаги – в других придётся составить схему или нарисовать рисунок. Может потребоваться калькулятор или какие-нибудь предметы домашнего обихода. Однако при всех различиях между этими задачами они сходны между собой в том, что для их решения требуется нестандартный подход и работа воображения, – поэтому они и называются занимательными. Решение этих задач способствует развитию внимания, памяти, гибкости ума, которую также часто называют смекалкой, или находчивостью.
Ко всем задачам приводятся ответы и комментарии, однако не спешите в них заглядывать, попытайтесь самостоятельно найти верное решение. Чем больше этих задач вы сможете решить, тем проще и легче будете в дальнейшем справляться с задачами подобного типа и даже научитесь самостоятельно их составлять.
Сборник задач поможет вам интересно и с пользой провести часы досуга, скоротать время в длительном путешествии, найти тему разговора или разрядить затянувшуюся неловкую паузу в беседе с малознакомыми людьми, а также он пригодиться в различных иных жизненных ситуациях.
1. В каждом из 10 мешков находится по 10 монет. Каждая монета весит 10 г. Но в одном мешке все монеты фальшивые – не по 10 г., а по 11 г. Как с помощью только одноразового взвешивания определить, в каком мешке находятся фальшивые монеты (все мешки пронумерованы от 1 до 10)? Мешки можно открывать и вытаскивать любое количество монет из каждого.
2. На всех трёх железных банках с печеньем перепутаны этикетки: «Овсяное печенье», «Песочное печенье» и «Шоколадное печенье». Банки закрыты, и вы можете взять только одно печенье из одной (любой) банки, а потом правильно расположить этикетки. Как это сделать?
3. В вашем шкафу лежит 22 синих носка и 35 чёрных носков.
Вам надо в полной темноте взять из шкафа пару носков. Сколько носков нужно взять, чтобы с гарантией получить совпадающую пару?
4. Старинным часам требуется 30 с, чтобы пробить 6 ч. За сколько секунд часы пробьют 12 ч?
5. В пруду растёт один лист лилии. Каждый день число листьев удваивается. На какой день пруд будет покрыт листьями лилии наполовину, если известно, что полностью он будет покрыт ими через 100 дней?
6. Пассажирский лифт поднимается на пятый этаж со скоростью вдвое большей, чем грузовой лифт, который идёт до третьего этажа.
Какой из этих двух лифтов придёт раньше: грузовой на третий этаж или пассажирский на пятый, если стартовали они с первого этажа одновременно?
7. Летит гусь. Навстречу ему – стая гусей. «Здравствуйте, 100 гусей,» – говорит он им. Они отвечают: «Нас не 100 гусей; вот если бы нас было столько, сколько сейчас, да ещё столько, да ещё пол-столько и четверть-столько, да ещё ты, вот тогда нас было бы 100 гусей».
Сколько гусей летит в стае?
8. Докажем, что 3 = 7. Известно, что если над каждой частью равенства проделать одну и ту же операцию, то равенство останется неизменным. Отнимем у каждой части нашего равенства по пять: 3 – 5 = 7 – 5. Получится: – 2 = 2. Теперь возведём каждую часть равенства в квадрат: (– 2)
2= 2
2. Получится: 4 = 4, следовательно: 3 = 7. Найдите ошибку в этом рассуждении.
9. Как известно, в любом атоме есть ядро, размеры которого меньше размеров самого атома. Если размер атомного ядра равен 10
–12см, а размер всего атома равен 10
–6см, следовательно, ядро по размеру меньше самого атома в 2 раза: 12 : 6 = 2. Верно ли это утверждение?
Если нет, то во сколько раз атомное ядро меньше атома?
10. Можно ли на самолёте долететь до Луны? Надо принять во внимание, что самолёты снабжены реактивными двигателями, как и космические ракеты, и работают на том же топливе, что и они.
11. Можно ли иголкой проколоть пятидесятикопеечную монету?
12. Стандартный стакан (200 г) наполнен водой до краёв. Сколько булавок можно в него накидать, чтобы из стакана не вылилось ни капли воды?
13. У Иванова в кабинете висит портрет. Иванова спрашивают: «Кто изображён на этом портрете?» Иванов путано отвечает:
«Отец изображённого на портрете есть единственный сын отца говорящего». Кто изображён на портрете?
14. Миссионер попал в плен к дикарям, которые посадили его в темницу и сказали: «Отсюда только два выхода – один на свободу, другой к гибели; выбраться тебе помогут два воина – один говорит всегда правду, другой всегда лжёт, но неизвестно, кто из них лжец, а кто правдолюбец; ты можешь задать любому из них только один вопрос». Какой вопрос надо задать, чтобы выбраться на свободу?
15. В монастыре висят две верёвки из редкостного шёлка. Они прикреплены к середине потолка на расстоянии одного метра друг от друга и достигают пола. Вор-акробат хочет украсть как можно больше верёвки. Высота потолка 20 м. Вор знает, что если он спрыгнет или упадёт с высоты более 5 м, то не сможет выбраться из монастыря. Поскольку лестницы у него нет, ему остаётся только лезть по верёвке. Он нашёл способ украсть обе верёвки почти целиком. Как это сделать?
16. Девушка ехала в такси. По пути она так много болтала, что шофёр занервничал. Он сказал ей, что очень сожалеет, но не слышит ни слова, – поскольку его слуховой аппарат не работает, он глух как пробка. Девушка замолчала, но, когда они доехали до места, поняла, что водитель над ней подшутил. Как она догадалась?
17. Вы находитесь в каюте стоящего на якоре океанского лайнера. В полночь вода была на 4 м ниже иллюминатора и поднималась на 0,5 м/ч. Если эта скорость удваивается каждый час, то за какое время вода достигнет иллюминатора?
18. Три путешественника прилегли отдохнуть в тени деревьев и уснули. Пока они спали, шутники вымазали углём их лбы. Проснувшись и взглянув друг на друга, они начали смеяться, причём каждому из них казалось, что двое других смеются друг над другом.
Внезапно один из них перестал смеяться, так как сообразил, что его собственный лоб тоже испачкан. Как он об этом догадался?
19. Сдвинув только одну их четырёх спичек, сделайте квадрат (рис. 45). Спички нельзя ни гнуть, ни ломать:
20. С восходом солнца путешественник начал подниматься по узкой, извилистой тропинке на вершину горы. Он шёл то быстрее, то медленнее, часто останавливаясь, чтобы отдохнуть. Проделав длинный путь, он достиг вершины только к закату солнца. Проведя ночь на вершине, с восходом солнца он отправился в обратный путь по той же тропинке. Спускался он также с неравномерной скоростью, неоднократно отдыхая по дороге, и к закату солнца достиг подножия горы. Понятно, что средняя скорость спуска превышала среднюю скорость подъёма. Есть ли на тропинке такая точка, которую путешественник проходил в одно и то же время суток как во время подъёма, так и во время спуска?
21. У скульптора есть 10 одинаковых статуй. Он хочет, чтобы у каждой из четырёх стен зала находилось по три статуи. Как их разместить?
22. Начертите, не отрывая карандаша от бумаги, следующие фигуры (рис. 46):
23. Один математик предложил торговцу такую сделку. Математик даёт торговцу 100 р., а торговец даёт математику взамен 1 к.
Каждый следующий день математик даёт торговцу на 100 р. больше, чем в предыдущий, т. е. на второй день он даёт ему 200 р., на третий – 300 р. и т. д. А торговец даёт математику взамен в два раза больше денег, чем в предыдущий день, т. е. на второй день он даёт ему 2 к., на третий – 4 к., на четвёртый – 8 к., на пятый – 16 к. и т. д.
Производить такой обмен они договорились в течение 30 дней. Кому из них этот обмен выгоден и почему?
24. Годовщина Октябрьской революции по старому стилю попадает на 25 октября, а по новому стилю – на 7 ноября. Таким образом, все события по старому стилю на 13 дней предшествуют тем же самым событиям по новому стилю. Значит, если по новому стилю Новый год приходится на 1 января, то по старому стилю он должен попадать на 19 декабря. Почему же мы тогда отмечаем старый Новый год 14 января?
25. Из спичек сделан рисунок рюмки, наполненной вином (рис. 47). Переставьте две спички так, чтобы на вновь получившем рисунке вино оказалось вне рюмки. При демонстрации роль вина может сыграть спичка:
26. Как расположить шесть сигарет таким образом, чтобы все они соприкасались друг с другом, т. е. чтобы каждая из них касалась пяти остальных?
27. Перед вами стоят три человека. Один из них Правдолюб (говорит всегда правду), другой Лжец (всегда лжёт), а третий Дипломат (то говорит правду, то лжёт). Вы не знаете, кто есть кто и задаёте вопрос человеку, который стоит слева:
– Кто стоит рядом с тобой?
– Правдолюб, – отвечает он.
Потом вы спрашиваете человека стоящего в центре:
– Кто ты?
– Дипломат, – отвечает тот.
И, наконец, вы спрашиваете человека, который стоит справа:
– Кто стоит рядом с тобой?
– Лжец, – отвечает он.
Кто же стоит слева, кто – справа, кто – в центре?
28. В десятилитровом ведре находится 10 л вина. В вашем распоряжении два пустых ведра: одно – 7 л, а другое – 3 л. Как с помощью этих вёдер путём переливаний разделить 10 л вина на две одинаковые части по 5 л?
29. У Андрея часы отстают на 10 мин, но он уверен, что они на 5 мин спешат. Он договорился с Катей встретиться в 8 ч 00 мин у электрички, чтобы поехать за город. У Кати часы на 5 мин спешат, но она думает, что они отстают на 10 мин. Кто из них первым придёт к поезду?
30. Черепаха, которой 110 лет, спросила динозавра: «Сколько тебе лет?» Динозавр, привыкший выражаться сложно и запутанно, ответил: «Мне сейчас в 10 раз больше лет, чем было тебе тогда, когда мне было столько же лет, сколько тебе сейчас». Сколько лет динозавру?
31. Угонщик похитил автомобиль, пытаясь пробраться в пункт
B, однако был обнаружен милицией в пункте
A. Уходя от погони, он начал петлять, двигаясь из
Aв
Bпо кривой
ACDBпо дугам малых полуокружностей так, как это показано стрелками (рис. 48). Преследовавшие его милиционеры стартовали из
Aмгновением позже и, надеясь перехватить угонщика в пункте
B, отправились по дуге большой полуокружности. Догонят ли они угонщика в пункте
B, если их скорости совершенно одинаковы (рис. 48)?
32. Кате вдвое больше лет, чем будет Насте тогда, когда Оле исполнится столько лет, сколько сейчас Кате. Кто из них самый старший по возрасту, а кто самый младший?
33. В одном классе ученики разделились на две группы. Одни должны были всегда говорить только правду, а другие – только неправду. Все ученики класса написали сочинение на свободную тему, а в конце сочинения каждый ученик должен был приписать одну из фраз: «Всё, здесь написанное, правда», «Всё, здесь написанное, ложь». Всего в классе было 17 правдолюбцев и 18 лжецов. Сколько сочинений с утверждением о правдивости написанного насчитал учитель при проверке работ?
34. Сколько всего прапрадедушек и прапрабабушек было у всех ваших прапрадедушек и прапрабабушек?
35. На столе лежит в разложенном виде носовой платок. На нём в центре стоит горлышком вниз пустая стеклянная бутылка. Как вытянуть платок из-под бутылки, не прикасаясь к ней?
36. В левой части равенства надо поставить только одну чёрточку (палочку) для того, чтобы равенство получилось истинным:
5 + 5 + 5 = 550.
37. Докажем, что три раза по два будет не шесть, а четыре.
Возьмём спичку, сломаем её пополам. Это один раз два. Потом возьмём половинку и сломаем её пополам. Это второй раз два. Затем возьмём оставшуюся половинку и её тоже сломаем пополам. Это третий раз два. Получилось четыре. Следовательно, три раза по два будет четыре, а не шесть. Найдите ошибку в этом рассуждении.
38. Как соединить девять точек между собой четырьмя линиями, не отрывая карандаша от бумаги (рис. 49)?
В магазине хозяйственных товаров покупатель спросил:
– Сколько стоит один?
– Двадцать рублей, – ответил продавец.
– Сколько стоит двенадцать?
– Сорок рублей.
– Хорошо, дайте мне сто двенадцать.
– Пожалуйста, с вас шестьдесят рублей.
Что покупал посетитель?
40. Если в 12 ч ночи идёт дождь, то можно ли ожидать, что через 72 ч будет солнечная погода?
41. Три человека заплатили за обед 30 р. (каждый по 10 р.). После их ухода хозяйка обнаружила, что обед стоит не 30 р., а 25 р. и отправила мальчика вдогонку, чтобы вернуть 5 р. Каждый из путников взял себе по 1 р., а 2 р. они оставили мальчику. Выходит, что каждый из них заплатил не по 10 р., а по 9 р. Их было трое: 9 · 3 = 27, и ещё два рубля у мальчика: 27 + 2 = 29. Куда делся рубль?
42. В бассейн площадью 1 га налили 1 000 000 л воды. Можно ли плавать в таком бассейне?
43. Что больше:
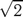
или
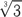
?
44. У одного мальчика не хватает до стоимости линейки 24 к., а у другого не хватает до этой стоимости 2 к. Когда они сложили свои деньги вместе, то всё равно не смогли купить линейку. Сколько стоит линейка?
45. В одном парламенте депутаты разделились на консерваторов и либералов. Консерваторы говорили по чётным числам только правду, а по нечётным – только неправду. Либералы, наоборот, говорили только правду по нечётным числам, а по чётным числам – только неправду. Каким образом с помощью одного вопроса, заданного любому депутату, можно точно установить, какое сегодня число: чётное или нечётное? Ответы должны быть определёнными: «да» или «нет».
46. Бутылка с пробкой стоит 1 р. 10 к. Бутылка дороже пробки на 1 р. Сколько стоит бутылка и сколько стоит пробка?
47. Катя живёт на четвёртом этаже, а Оля – на втором. Поднимаясь на четвёртый этаж, Катя преодолевает 60 ступенек. Сколько ступенек надо пройти Оле, чтобы подняться на второй этаж?
48. Математик написал на листке двузначное число. Когда он перевернул листок вверх ногами, число уменьшилось на 75. Какое число было написано?
49. Прямоугольный лист бумаги сложили пополам 6 раз. На сложенном листе, не на сгибах, сделали 2 дырки. Сколько дырок будет на листе, если его развернуть?
50. Два отца и два сына поймали трёх зайцев: каждый по одному.
Как такое возможно?
51. Собеседник предлагает вам задумать любое трёхзначное число. Потом он просит продублировать его, чтобы получилось шестизначное число. Например, вы задумали число 389, продублировав его, получаете шестизначное число – 389 389; или 546 – 546 546 и т. п.
Далее собеседник предлагает вам это шестизначное число разделить на 13. «Вдруг получится без остатка», – говорит он. Вы производите деление с помощью калькулятора (можно и без него) и действительно ваше число делится на 13 без остатка. Далее он предлагает вам получившийся результат разделить на 11. Вы делите, и опять получается без остатка. И, наконец, собеседник просит вас разделить получившийся результат на 7. Деление не только проходит без остатка, но и даёт в результате то самое трёхзначное число, которое вы произвольно выбрали сначала. Каким образом это происходит?
52. Разделите фигуру, состоящую из трёх одинаковых квадратов, на четыре равные части (рис. 50):
53. Сто школьников одновременно изучали английский и немецкий языки. По окончании курсов они сдавали экзамен, который показал, что 10 школьников не освоили ни тот, ни другой язык. Из оставшихся немецкий сдали 75 человек, а 83 выдержали экзамен по английскому. Сколько экзаменовавшихся владеет обоими языками?
54. Каким образом из кружки, ковшика, кастрюли и любой другой посуды правильной цилиндрической формы, наполненной до краёв водой, отлить ровно половину, не используя никаких измерительных приборов?
55. Часовая и минутная стрелки иногда совпадают, например в 12 ч или в 24 ч. Сколько раз они совпадут между 6 ч утра одного дня и 10 ч вечера другого дня?
56. Теплоход доплывает от Нижнего Новгорода до Астрахани за 5 суток, обратный путь он проделывает с той же скоростью за 7 суток. За сколько суток от Нижнего Новгорода до Астрахани доплывёт плот?
57. Три курицы несут три яйца за три дня. Сколько яиц снесут 12 куриц за 12 дней?
58. Как написать число 100 с помощью пяти единиц и знаков действий?
59. Давайте подсчитаем, сколько дней в году мы работаем, а сколько отдыхаем. В году 365 дней. Восемь часов в день уходит у каждого на сон – это 122 дня ежегодно. Вычитаем, остаётся 243 дня. Восемь часов в день занимает отдых после работы, это тоже 122 дня в год. Вычитаем, остаётся 121 день. По выходным, которых в году 52, никто не работает. Вычитаем, остаётся 69 дней. Далее, четырёхнедельный отпуск – это 28 дней. Вычитаем, остаётся 41 день. Примерно 11 дней в году занимают различные праздники. Вычитаем, остаётся 30 дней. Таким образом, мы работаем всего один месяц в году.
Верно ли это рассуждение? Если нет, то какая ошибка в нём допущена?
60. В один ряд стоят три наполненных водой стакана и три пустых (рис. 51). Каким образом сделать так, чтобы наполненные и пустые стаканы чередовались, если можно взять в руки только один стакан?
61. Если 1 рабочий может построить дом за 12 дней, то 12 рабочих построят его за 1 день. Следовательно, 288 рабочих построят дом за 1 ч, 17 280 рабочих построят его за 1 мин, а 1 036 800 рабочих смогут построить дом за 1 с. Верно ли это рассуждение? Если нет, то в чём заключается ошибка?
62. Какое слово всегда пишется неправильно? (Задача-шутка.)
63. «Ручаюсь, – сказал продавец в зоомагазине, – что этот попугай будет повторять любое услышанное слово». Обрадованный покупатель приобрёл чудо-птицу, но, придя домой, обнаружил, что попугай нем, как рыба. Тем не менее, продавец не лгал. Как такое возможно? (Задача-шутка.)
64. В комнате есть свеча и керосиновая лампа. Что вы зажжёте первым, когда вечером войдёте в эту комнату?
65. Пётр сильно устал и лёг спать в 7 ч вечера, поставив механический будильник на 9 ч утра. Сколько часов ему удастся поспать?
66. Отрицание истинного предложения является ложным предложением, а отрицание ложного – истинным. Однако следующий пример говорит, что это как будто, не всегда так. Предложение: «Это предложение содержит шесть слов», – является ложным, поскольку в нём не шесть, а пять слов. Но отрицание: – «Это предложение не содержит шесть слов», – также является ложным, так как в нём как раз шесть слов. Как разрешить это недоразумение?
67. Сколько существует восьмизначных чисел, сумма цифр которых равна двум?
68. Периметр фигуры, составленной из квадратов, равен шести (рис. 52). Чему равна её площадь?
69. Чему равна разность куба суммы квадратов чисел 2 и 3 и квадрата суммы их кубов?
70. Половина от половины числа равна половине. Какое это число?
71. Со временем человек обязательно побывает на Марсе. Саша Иванов – это человек. Следовательно, Саша Иванов со временем обязательно побывает на Марсе. Верно ли это рассуждение? Если нет, то какая ошибка в нём допущена?
72. Для получения оранжевой краски надо смешать 6 частей жёлтой краски с 2 частями красной. Есть 3 г жёлтой краски и 3 г красной.
Сколько граммов оранжевой краски можно получить в этом случае?
73. Из 12 спичек составлено 4 квадрата (рис. 53). Каким образом надо убрать 2 спички, чтобы осталось 2 квадрата?
74. Какой знак надо поставить между числами 5 и 6, чтобы получившееся число было больше 5, но меньше 6?
5 < 5 ? 6 < 6
75. В футбольной команде 11 игроков. Их средний возраст равен 22 годам. Во время матча один из игроков выбыл. При этом средний возраст команды стал равен 21 году. Сколько лет выбывшему игроку?
76. – Сколько лет твоему отцу? – спрашивают мальчика.
– Столько же, сколько и мне, – невозмутимо отвечает он.
– Как такое возможно?
– Очень просто: мой отец стал моим отцом только тогда, когда я родился, ведь до моего рождения он не был моим отцом, значит моему отцу столько же лет, сколько и мне.
Верно ли это рассуждение? Если нет, то какая ошибка в нём допущена?
77. В мешке 24 кг гвоздей. Каким образом можно на чашечных весах без гирь отмерить 9 кг гвоздей?
78. Пётр лгал с понедельника по среду и говорил правду в другие дни, а Иван лгал с четверга по субботу и говорил правду в другие дни. Однажды они одинаково сказали: «Вчера был один из дней, когда я лгу». Какой день был вчера?
79. Трёхзначное число записали цифрами, а потом – словами. Получилось, что все цифры в этом числе разные и возрастают слева направо, а все слова начинаются с одной и той же буквы. Какое это число?
80. В равенстве, составленном из спичек:
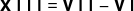
, допущена ошибка. Каким образом надо переложить одну спичку, чтобы равенство стало верным?
81. Во сколько раз увеличится трёхзначное число, если к нему приписать такое же число?
82. Если бы не было времени, то не было бы ни одного дня. Если бы не было ни одного дня, то всегда стояла бы ночь. Но если бы всегда стояла ночь, то было бы время. Следовательно, если бы не было времени, оно было бы. В чём заключается причина данного недоразумения?
83. В каждой из двух корзин по 12 яблок. Настя взяла несколько яблок из первой корзины, а Маша взяла из второй столько, сколько осталось в первой. Сколько яблок осталось в двух корзинах вместе?
84. У одного фермера 8 свиней: 3 розовые, 4 бурые и 1 чёрная.
Сколько свиней могут сказать, что в этом небольшом стаде найдётся, по крайней мере, ещё одна свинья такой же масти, как и её собственная? (Задача-шутка.)
85. Единственный сын отца сапожника – плотник. Кем приходится сапожник плотнику?
86. Если 1 рабочий может построить дом за 5 дней, значит, 5 рабочих построят его за 1 день. Следовательно, если 1 корабль пересекает Атлантический океан за 5 дней, то 5 кораблей пересекут его за 1 день. Верно ли это утверждение? Если нет, то в чём заключается допущенная в нём ошибка?
87. Возвращаясь из школы, Петя и Саша зашли в магазин, где они увидели большие весы.
– Давай взвесим наши портфели, – предложил Петя.
Весы показали, что Петин портфель весит 2 кг, а вес Сашиного портфеля оказался равным 3 кг. Когда мальчики взвесили два портфеля вместе, весы показали 6 кг.
– Как же так? – удивился Петя. – Ведь 2 плюс 3 не равно 6.
– Ты что, не видишь? – ответил ему Саша. – У весов сдвинута стрелка.
Каков вес портфелей на самом деле?
88. Как разместить 6 кружочков на плоскости таким образом, чтобы получилось 3 ряда по 3 кружочка в каждом ряду?
89. После семи стирок длина, ширина и высота куска мыла уменьшилась вдвое. На сколько стирок хватит оставшегося куска?
90. Как от куска материи в 2/3 м отрезать 1/2 м без помощи каких-либо измерительных приборов?
91. Часто говорят, что композитором, или художником, или писателем, или учёным надо родиться. Верно ли это? Действительно ли композитором (художником, писателем, учёным) надо родиться?
(Задача-шутка.)
92. Для того чтобы видеть, совсем не обязательно иметь глаза.
Без правого глаза мы видим. Без левого тоже видим. А поскольку кроме левого и правого глаза других глаз у нас нет, то оказывается, что ни один глаз не является необходимым для зрения. Верно ли это утверждение? Если нет, то какая ошибка в нём допущена?
93. Попугай прожил меньше 100 лет и умеет отвечать только на вопросы «да» и «нет». Сколько вопросов ему надо задать, чтобы узнать его возраст?
94. Скажите, сколько кубиков изображено на рисунке 54:





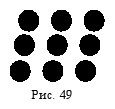
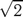 или
или
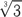 ?
?



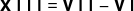 , допущена ошибка. Каким образом надо переложить одну спичку, чтобы равенство стало верным?
, допущена ошибка. Каким образом надо переложить одну спичку, чтобы равенство стало верным?