 |
|
ѕопул€рные авторы:: Ѕ—Ё :: √рин јлександр :: –аззаков ‘едор :: артленд Ѕарбара :: „ехов јнтон ѕавлович :: √орький ћаксим :: ларк јртур „арльз :: јзимов јйзек :: Ѕорхес ’орхе Ћуис :: Ћавкрафт √овард ‘иллипс ѕопул€рные книги:: ƒюна ( ниги 1-3) :: —правочник по реестру Windows XP :: ’рустальна€ пробка :: ƒело плем€нницы лунатика :: «ов любви :: —олнечный ветер :: The Boarding House :: —екретные материалы (ѕилот) :: Ћюбовь всегда выигрывает :: ƒама с собачкой |
—тоунхендж и пирамиды ≈гиптаModernLib.Net / Ќаучно-образовательна€ / ‘арлонг ƒевид / —тоунхендж и пирамиды ≈гипта - „тение (стр. 9)
–Т—Б–µ —Н—В–Њ, –Ї–Њ–љ–µ—З–љ–Њ –ґ–µ, –ї–Є—И—М –і–Њ–≥–∞–і–Ї–Є –Є –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ —А–µ—И–Є—В–µ–ї—М–љ—Л–є –Њ—В–Ї–∞–Ј –Њ—В —В–Њ–≥–Њ, —З—В–Њ —Е–Њ—В–µ–ї–Є –±—Л –љ–∞–≤—П–Ј–∞—В—М –љ–∞–Љ –Њ—А—В–Њ–і–Њ–Ї—Б–∞–ї—М–љ—Л–µ –µ–≥–Є–њ—В–Њ–ї–Њ–≥–Є –Э–Њ —Н—В–Њ –њ–Њ–і—А–∞–Ј—Г–Љ–µ–≤–∞–µ—В –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М –≤ –Ј–∞–Љ—Л—Б–ї–µ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–∞ –У–Є–Ј—Л, –Ї–Њ—В–Њ—А–∞—П –±—Л–ї–∞ –њ—А–Є–Ј–љ–∞–љ–∞ —В–Њ–ї—М–Ї–Њ –њ–Њ—Б–ї–µ —В–Њ–≥–Њ, –Ї–∞–Ї —А–∞–±–Њ—В–∞ –С—М—О–≤—Н–ї–∞ –Є –Ф–ґ–Є–ї–±–µ—А—В–∞ —Б–≤—П–Ј–∞–ї–∞ –µ–≥–Њ —Б —В—А–µ–Љ—П-–Ј–≤–µ–Ј–і–∞–Љ–Є –Я–Њ—П—Б–∞ –Ю—А–Є–Њ–љ–∞, –Є –Њ—В—Б—О–і–∞ –љ–∞—З–Є–љ–∞–µ—В—Б—П –љ–Њ–≤—Л–є –њ—Г—В—М –Є–Ј—Г—З–µ–љ–Є—П –Ј–љ–∞—З–µ–љ–Є—П –њ–Є—А–∞–Љ–Є–і. –Ъ–∞–Ї–Є–Љ–Є –±—Л –≤–∞–ґ–љ—Л–Љ–Є –љ–Є –±—Л–ї–Є —З–Є—Б–ї–∞ –і–ї—П –і—А–µ–≤–љ–Є—Е –Ї—Г–ї—М—В—Г—А, –Њ–љ–Є –љ–µ –±—Л–ї–Є –њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ—Л–Љ –Є—Б—В–Њ—З–љ–Є–Ї–Њ–Љ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Ј–љ–∞–љ–Є—П. –Я–ї–∞—В–Њ–љ —Г—В–≤–µ—А–ґ–і–∞–ї, —З—В–Њ –≤—Б–µ –≤–µ—З–љ—Л–µ –Є—Б—В–Є–љ—Л –Љ–Њ–≥—Г—В –±—Л—В—М –њ–Њ–ї—Г—З–µ–љ—Л —Б –њ–Њ–Љ–Њ—Й—М—О —Ж–Є—А–Ї—Г–ї—П –Є –ї–Є–љ–µ–є–Ї–Є. –Ш–љ—Л–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, —З–Є—Б—В–∞—П –≥–µ–Њ–Љ–µ—В—А–Є—П –ї–µ–ґ–Є—В –≤ —Ж–µ–љ—В—А–µ –≤—Б–µ—Е –≤–µ—Й–µ–є. –І–Є—Б—В–∞—П –≥–µ–Њ–Љ–µ—В—А–Є—П –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ –Ї–∞–Ї —А–Є—Б—Г–љ–Ї–Є, –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ —Б –њ–Њ–Љ–Њ—Й—М—О —Ж–Є—А–Ї—Г–ї—П –Є –ї–Є–љ–µ–є–Ї–Є –±–µ–Ј–Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Ї —З–Є—Б–ї–∞–Љ –Є –Љ–µ—А–∞–Љ. –Х—Й–µ –Њ–і–Є–љ –Ї–ї—О—З –Ї –≥–Њ–ї–Њ–≤–Њ–ї–Њ–Љ–Ї–µ –і–∞–µ—В –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–∞—П –Њ—Б–љ–Њ–≤–∞ –Њ—А–Є–µ–љ—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–ї–∞–љ–∞ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–∞ –У–Є–Ј—Л. –Ф–ї—П –њ–Њ–љ–Є–Љ–∞–љ–Є—П —Б–Љ—Л—Б–ї–∞ —Б—Е–µ–Љ—Л, –Њ–±–љ–∞—А—Г–ґ–µ–љ–љ–Њ–є –≤ –Ь–∞—А–ї–±–Њ—А–Њ-–Ф–∞—Г–љ—Б, –Є –µ–µ —Б–≤—П–Ј–Є —Б –Т–µ–ї–Є–Ї–Њ–є –њ–Є—А–∞–Љ–Є–і–Њ–є –Х–≥–Є–њ—В–∞ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –њ—А–µ–ґ–і–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞—В—М –Ї–Њ–љ—Ж–µ–њ—Ж–Є–Є —Б–≤—П—Й–µ–љ–љ–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є–Є. –У–ї–∞–≤–∞ 6 –С–Њ–ї—М—И–∞—П –≥–∞–ї–µ—А–µ—П –њ–Є—А–∞–Љ–Є–і—Л –≤—Л—Б—В—А–Њ–µ–љ–∞ –љ–∞ –Њ–і–љ–Њ–є –ї–Є–љ–Є–Є —Б —Ж–µ–љ—В—А–Њ–Љ –Њ–і–љ–Њ–≥–Њ –Є–Ј –Ї—А—Г–≥–Њ–≤. –Э–∞–і–њ–Є—Б—М –љ–∞–і –≤—Е–Њ–і–Њ–Љ –≤ –Р–Ї–∞–і–µ–Љ–Є—О –Я–ї–∞—В–Њ–љ–∞ –≤ –Р—Д–Є–љ–∞—Е –≥–ї–∞—Б–Є–ї–∞: ¬Ђ–Я—Г—Б—В—М –≤–Њ–є–і–µ—В —Б—О–і–∞ —Б–≤–µ–і—Г—Й–Є–є –≤ –≥–µ–Њ–Љ–µ—В—А–Є–Є¬ї. –Ф–ї—П –і—А–µ–≤–љ–Є—Е –≥—А–µ–Ї–Њ–≤ —З–Є—Б—В–∞—П –≥–µ–Њ–Љ–µ—В—А–Є—П –±—Л–ї–∞ —Ж–µ–љ—В—А–Њ–Љ –≤—Б–µ—Е –≤–µ—Й–µ–є. –Ю–љ–∞ –±—Л–ї–∞ —Б–њ–Њ—Б–Њ–±–Њ–Љ –њ—А–Є–Љ–Є—А–µ–љ–Є—П –Љ–Є—А–∞ –±–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–≥–Њ —Б —Д–Њ—А–Љ–Њ–є –≤–Є–і–Є–Љ–Њ–≥–Њ –Љ–Є—А–∞. –Ч–Њ–ї–Њ—В–∞—П –њ—А–Њ–њ–Њ—А—Ж–Є—П, –љ–∞–њ—А–Є–Љ–µ—А, –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–њ–Є—Б–∞–љ–∞ –љ–∞ —П–Ј—Л–Ї–µ –≥–µ–Њ–Љ–µ—В—А–Є–Є, –љ–Њ –љ–µ —З–Є—Б–µ–ї. –Ю–љ–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –љ–∞—З–µ—А—В–∞–љ–∞, –љ–Њ –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Ј–∞–њ–Є—Б–∞–љ–∞, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –Є–Љ–µ–µ—В –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ–µ —З–Є—Б–ї–Њ –і–µ—Б—П—В–Є—З–љ—Л—Е –Ј–љ–∞–Ї–Њ–≤. –У–µ–Њ–Љ–µ—В—А–Є—О –Љ–Њ–ґ–љ–Њ —Б—З–Є—В–∞—В—М —Б–њ–Њ—Б–Њ–±–Њ–Љ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —В–Њ–≥–Њ, —З—В–Њ –Є–љ–∞—З–µ –љ–µ–Њ–њ—А–µ–і–µ–ї–Є–Љ–Њ. –Ю–± –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–Є —З–Є—Б—В–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є–Є –≤ –Ф—А–µ–≤–љ–µ–Љ –Х–≥–Є–њ—В–µ –Љ—Л –Ј–љ–∞–µ–Љ –Њ—З–µ–љ—М –Љ–∞–ї–Њ. –Ь—Л –љ–µ —А–∞—Б–њ–Њ–ї–∞–≥–∞–µ–Љ –њ–∞–њ–Є—А—Г—Б–∞–Љ–Є, –і–∞–≤–∞–≤—И–Є–Љ–Є –±—Л –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В —Г—А–∞–≤–љ–µ–љ–Є–є –Я–ї–∞—В–Њ–љ–∞, –§–∞–ї–µ—Б–∞ –Є –≠–≤–Ї–ї–Є–і–∞, –Њ–ї–Є—Ж–µ—В–≤–Њ—А—П—О—Й–Є—Е –і—А–µ–≤–љ–µ–≥—А–µ—З–µ—Б–Ї—Г—О –Љ—Л—Б–ї—М. –Ґ–µ–Љ –љ–µ –Љ–µ–љ–µ–µ –Я–ї–∞—В–Њ–љ —Б—З–Є—В–∞–ї, —З—В–Њ –Х–≥–Є–њ–µ—В –≤–ї–∞–і–µ–ї —Б–Њ–≤–Њ–Ї—Г–њ–љ–Њ—Б—В—М—О –≥–ї—Г–±–Њ–Ї–Є—Е –Ј–љ–∞–љ–Є–Є, –Њ—Б–љ–Њ–≤–∞–љ–љ—Л—Е –љ–∞ –≥–∞—А–Љ–Њ–љ–Є–Є –Є –њ—А–Њ–њ–Њ—А—Ж–Є–Є. –Ь—Л –Љ–Њ–ґ–µ–Љ —Б–і–µ–ї–∞—В—М –≤—Л–≤–Њ–і, —З—В–Њ –і—А–µ–≤–љ–Є–µ –µ–≥–Є–њ—В—П–љ–µ –љ–µ –Љ–µ–љ–µ–µ –Є—Б–Ї—Г—Б–љ–Њ –≤–ї–∞–і–µ–ї–Є —Ж–Є—А–Ї—Г–ї–µ–Љ –Є –ї–Є–љ–µ–є–Ї–Њ–є, —З–µ–Љ –Є—Е –≥—А–µ—З–µ—Б–Ї–Є–µ –Ї–Њ–ї–ї–µ–≥–Є. –≠—В–Є –Ј–љ–∞–љ–Є—П –і–Њ–ї–ґ–љ—Л –±—Л–ї–Є –њ–Њ–≤–ї–Є—П—В—М –љ–∞ –Є—Е –Є—Б–Ї—Г—Б—Б—В–≤–Њ –Є –∞—А—Е–Є—В–µ–Ї—В—Г—А—Г. –†–∞–Ј–≥–∞–і–Ї–∞ —В–Њ–≥–Њ, –Ї–∞–Ї –µ–≥–Є–њ—В—П–љ–µ –≤—Л–±–Є—А–∞–ї–Є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–≤—И–Є–µ—Б—П –Є–Љ–Є –њ—А–Њ–њ–Њ—А—Ж–Є–Є, —П–≤–ї—П–µ—В—Б—П —Б–њ–Њ—Б–Њ–±–Њ–Љ –≤–Њ–Ј–≤—А–∞—Й–µ–љ–Є—П –Ї –Є—Б—В–Њ–Ї–∞–Љ –Є—Е —Ж–Є–≤–Є–ї–Є–Ј–∞—Ж–Є–Є. –£–Ј–Њ—А—Л –љ–∞ –Ь–∞—А–ї–±–Њ—А–Њ-–Ф–∞—Г–љ—Б —В–∞–Ї–ґ–µ –њ—А–µ–і—Б—В–∞–≤–ї—П—О—В—Б—П –Њ—Б–љ–Њ–≤–∞–љ–љ—Л–Љ–Є –љ–∞ —З–Є—Б—В–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є–Є. –Э–∞—И–Є–Љ —Б–ї–µ–і—Г—О—Й–Є–Љ —И–∞–≥–Њ–Љ –њ–Њ—Н—В–Њ–Љ—Г —Б—В–∞–љ–µ—В —Б–±–ї–Є–ґ–µ–љ–Є–µ —Н—В–Є—Е –љ–µ—Б–Њ–Є–Ј–Љ–µ—А–Є–Љ—Л—Е —З–∞—Б—В–µ–є –≥–Њ–ї–Њ–≤–Њ–ї–Њ–Љ–Ї–Є –Є –Њ—В–Ї—А—Л—В–Є–µ –≥–µ–Њ–Љ–µ—В—А–Є–Є, –ї–µ–ґ–∞—Й–µ–є –≤ –Є—Е –Њ—Б–љ–Њ–≤–µ –Є –Њ–±—К–µ–і–Є–љ—П—О—Й–µ–є –Є—Е. –Ґ–µ—А–Љ–Є–љ ¬Ђ—Б–≤—П—Й–µ–љ–љ–∞—П –≥–µ–Њ–Љ–µ—В—А–Є—П¬ї –Љ–Њ–ґ–µ—В –≤–≤–µ—Б—В–Є –≤ –Ј–∞–±–ї—Г–ґ–і–µ–љ–Є–µ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –Њ—Б–љ–Њ–≤—Л –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є –њ—А–Њ–њ–Њ—А—Ж–Є–Є —И–Є—А–Њ–Ї–Њ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ—Л –≤ –њ—А–Є—А–Њ–і–µ, –∞ —В–∞–Ї–ґ–µ –≤ –Є—Б–Ї—Г—Б—Б—В–≤–µ –Є –∞—А—Е–Є—В–µ–Ї—В—Г—А–µ. –Я–Њ—З–µ–Љ—Г –Њ–і–љ–Є —Н–ї–µ–Љ–µ–љ—В—Л —Б–≤—П—Й–µ–љ–љ—Л, –∞ –і—А—Г–≥–Є–µ –љ–µ—В? –Э–µ–ї–µ–≥–Ї–Њ –Њ—В–≤–µ—В–Є—В—М –љ–∞ —Н—В–Њ—В –≤–Њ–њ—А–Њ—Б. –Ґ–µ–Љ –љ–µ –Љ–µ–љ–µ–µ —Б—В–∞–ї–Њ —Г–ґ–µ —В—А–∞–і–Є—Ж–Є–µ–є –і–µ–ї–∞—В—М –Њ—Б–Њ–±—Л–є –∞–Ї—Ж–µ–љ—В –љ–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–љ—Л—Е –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е –Њ—В–љ–Њ—И–µ–љ–Є—П—Е –Є –њ—А–Њ–њ–Њ—А—Ж–Є—П—Е, —З–∞—Й–µ –≤—Б–µ–≥–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–≤—И–Є—Е—Б—П –≤ –њ—А–Њ–µ–Ї—В–∞—Е –њ–Њ—Б—В—А–Њ–µ–Ї —А–µ–ї–Є–≥–Є–Њ–Ј–љ–Њ–≥–Њ –њ—А–µ–і–љ–∞–Ј–љ–∞—З–µ–љ–Є—П. –Ю–±—Л—З–љ–Њ–Љ—Г –љ–∞–±–ї—О–і–∞—В–µ–ї—О —Н—В–Є –њ—А–Њ–њ–Њ—А—Ж–Є–Є –њ—А–Њ—Б—В–Њ –њ—А–Є—П—В–љ—Л. –Т —Е—Г–і–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–Љ –њ–ї–∞–љ–µ –Њ–љ–Є –∞–љ–∞–ї–Њ–≥–Є—З–љ—Л –Љ—Г–Ј—Л–Ї–µ. –° –њ–Њ–Љ–Њ—Й—М—О —А–∞–Ј–ї–Є—З–љ—Л—Е —Б–Њ—З–µ—В–∞–љ–Є–є –љ–Њ—В –Є —Б–≤–Њ–є—Б—В–≤ –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М –≥–∞—А–Љ–Њ–љ–Є—З–љ—Л–µ –Є —А–µ–Ј–Њ–љ–Є—А—Г—О—Й–Є–µ –Ј–≤—Г–Ї–Є. –Ю–њ—А–µ–і–µ–ї–µ–љ–љ—Л–µ –Љ–µ–ї–Њ–і–Є–Є –≤—А–Њ–і–µ –≥—А–Є–≥–Њ—А–Є–∞–љ—Б–Ї–Є—Е —Е–Њ—А–∞–ї–Њ–≤ –љ–∞–≤–µ–≤–∞—О—В –≤–Њ–Ј–≤—Л—И–µ–љ–љ—Л–µ —З—Г–≤—Б—В–≤–∞. –Ф—А—Г–≥–∞—П –Љ—Г–Ј—Л–Ї–∞ –њ–Њ–Ј–≤–Њ–ї—П–µ—В –љ–∞–Љ —Б–Њ–њ—А–Є–Ї–Њ—Б–љ—Г—В—М—Б—П –љ–µ–њ–Њ—Б—А–µ–і —Б—В–≤–µ–љ–љ–Њ —Б —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–Љ–Є —Н–Љ–Њ—Ж–Є—П–Љ–Є. 
–Т–µ–ї–Є–Ї–Є–є –ґ–µ —Д–Є–ї–Њ—Б–Њ—Д –Я–Є—Д–∞–≥–Њ—А –њ–Њ–Ї–∞–Ј–∞–ї —Б–≤—П–Ј–Є –Љ–µ–ґ–і—Г –Љ—Г–Ј—Л–Ї–Њ–є, –Ј–≤—Г–Ї–Њ–Љ, —З–Є—Б–ї–Њ–Љ –Є —Д–Њ—А–Љ–Њ–є. –Т —А–µ–ї–Є–≥–Є–Њ–Ј–љ–Њ–є —В—А–∞–і–Є—Ж–Є–Є —Ж–µ–љ—В—А–∞–ї—М–љ—Л–Љ–Є —П–≤–ї—П—О—В—Б—П —В—А–Є –Њ—Б–љ–Њ–≤–љ—Л–µ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ —Д–Є–≥—Г—А—Л, –Ї—А—Г–≥, —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Є –Ї–≤–∞–і—А–∞—В (—А–Є—Б. 29). –°—З–Є—В–∞–ї–Њ—Б—М, —З—В–Њ –Њ–љ–Є –њ—А–µ–і—Б—В–∞–≤–ї—П—О—В —В—А–Є —Г—А–Њ–≤–љ—П –љ–∞—И–µ–≥–Њ –±—Л—В–Є—П: –і—Г—Е, —А–∞–Ј—Г–Љ –Є —В–µ–ї–Њ. –Э–Є–Ї–Њ–Љ—Г –љ–µ –Є–Ј–≤–µ—Б—В–љ–Њ, –Ї—В–Њ –њ–µ—А–≤—Л–Љ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї —Ж–Є—А–Ї—Г–ї—М, –Ї–∞–Ї –Є —Б–Є—Б—В–µ–Љ—Л —Б—З–µ—В–∞. –Т–µ—А–Њ—П—В–љ–Њ, –њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ —А–µ—З—М —И–ї–∞ –Њ —И–љ—Г—А–Ї–µ –љ–∞ –і–≤—Г—Е –Ї–Њ–ї—Л—И–Ї–∞—Е, –Ї–Њ—В–Њ—А—Л–µ –Є –њ—А–Њ–ї–Њ–ґ–Є–ї–Є –њ—Г—В—М —Б–Є–Љ–≤–Њ–ї–Є—З–µ—Б–Ї–Њ–Љ—Г –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—О —Ж–∞—А—Б—В–≤–∞ –Є–і–µ–є –Є —Д–Њ—А–Љ. –Т—Б–µ –њ—А–∞–≤–Є–ї—М–љ—Л–µ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ —Д–Є–≥—Г—А—Л –Љ–Њ–≥—Г—В –±—Л—В—М –њ–Њ–ї—Г—З–µ–љ—Л —Б –њ–Њ–Љ–Њ—Й—М—О —Ж–Є—А–Ї—Г–ї—П –С–Њ–≥–∞, –Ї–Њ—В–Њ—А–Њ–≥–Њ –њ–Њ—А–Њ–є –љ–∞–Ј—Л–≤–∞–ї–Є ¬Ђ–Т–µ–ї–Є–Ї–Є–Љ –У–µ–Њ–Љ–µ—В—А–Њ–Љ¬ї, —З–∞—Б—В–Њ –Є–Ј–Њ–±—А–∞–ґ–∞–ї–Є –њ–Њ–ї—М–Ј—Г—О—Й–Є–Љ—Б—П —Ж–Є—А–Ї—Г–ї–µ–Љ. –° –≥–µ–Њ–Љ–µ—В—А–Є–µ–є –±—Л–ї–Њ —Б–≤—П–Ј–∞–љ–Њ –Є –Є–Ј—Г—З–µ–љ–Є–µ —З–Є—Б–µ–ї. –Ш–і–µ–∞–ї—М–љ—Л–Љ–Є —Б—З–Є—В–∞–ї–Є —Ж–µ–ї—Л–µ —З–Є—Б–ї–∞ вАУ –≤ –љ–Є—Е –≤–Є–і–µ–ї–∞—Б—М –Ј–∞–Ї–Њ–љ—З–µ–љ–љ–Њ—Б—В—М. –Ф—А–Њ–±–Є –ґ–µ –њ—А–µ–і—Б—В–∞–≤–ї—П–ї–Є —Б–Њ–±–Њ–є —З–Є—Б–ї–∞ –≤ —Б—В–∞–і–Є–Є —Б—В–∞–љ–Њ–≤–ї–µ–љ–Є—П –Т —Н—В–Њ–Љ —Б–Љ—Л—Б–ї–µ –Њ–љ–Є –њ–Њ—А–Њ–є —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–ї–Є—Б—М –Ї–∞–Ї –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–∞—П —Б–Є–ї–∞ –±–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–≥–Њ –≤ –і–≤–Є–ґ–µ–љ–Є–Є —З–µ—А–µ–Ј –Љ–Є—А–Њ–Ј–і–∞–љ–Є–µ. –¶–µ–ї—Л–µ —З–Є—Б–ї–∞ –њ–Њ–Ј–љ–∞–≤–∞–µ–Љ—Л, –љ–Њ —В–∞–Ї–Є–µ –Њ—В–љ–Њ—И–µ–љ–Є—П, –Ї–∞–Ї —З–Є—Б–ї–Њ –њ–Є (ѕА), –Љ–Њ–≥—Г—В –±—Л—В—М —В–Њ–ї—М–Ї–Њ –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–∞—Ж–Є—П–Љ–Є –Є –њ–Њ—В–Њ–Љ—Г –љ–µ–њ–Њ–Ј–љ–∞–≤–∞–µ–Љ—Л. –Ґ–Њ –±—Л–ї–∞ –љ–µ–њ–Њ—Б—В–Є–ґ–Є–Љ–∞—П —А—Г–Ї–∞ –С–Њ–≥–∞, –њ—А–Њ–љ–Є–Ї–∞—О—Й–∞—П –≤–Њ –≤—Б–µ –≤–µ—Й–Є. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Њ—В–і–µ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ —П–≤–ї—П—О—В—Б—П –ї–Є–±–Њ —А–∞—Ж–Є–Њ–љ–∞–ї—М–љ—Л–Љ–Є (—Ж–µ–ї—Л–µ —З–Є—Б–ї–∞), –ї–Є–±–Њ –Є—А—А–∞—Ж–Є–Њ–љ–∞–ї—М–љ—Л–Љ–Є (–і—А–Њ–±–љ—Л–µ —З–Є—Б–ї–∞), –≥–µ–Њ–Љ–µ—В—А–Є—П –Љ–Њ–ґ–µ—В –љ–∞–≤–µ—Б—В–Є –Љ–Њ—Б—В—Л –Љ–µ–ґ–і—Г –љ–Є–Љ–Є. –Ъ—А—Г–≥ –Љ–Њ–ґ–µ—В –њ—А–µ–і—Б—В–∞–≤–ї—П—В—М –Ї–∞–Ї –њ—А–Є–љ—Ж–Є–њ —А–∞—Ж–Є–Њ–љ–∞–ї—М–љ–Њ–≥–Њ —Ж–µ–ї–Њ–≥–Њ —З–Є—Б–ї–∞ –≤ —Б–≤–Њ–µ–Љ –і–Є–∞–Љ–µ—В—А–µ, —В–∞–Ї –Є –Є—А—А–∞—Ж–Є–Њ–љ–∞–ї—М–љ—Г—О —Д—Г–љ–Ї—Ж–Є—О –≤ —Б–≤–Њ–µ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –Ъ–≤–∞–і—А–∞—В –Є –µ–≥–Њ –і–Є–∞–≥–Њ–љ–∞–ї—М —В–∞–Ї–ґ–µ –і–∞—О—В –њ–Њ—Е–Њ–ґ–Є–є —Д–µ–љ–Њ–Љ–µ–љ. –Э–∞–њ—А–Є–Љ–µ—А, –і–Є–∞–≥–Њ–љ–∞–ї—М –Ї–≤–∞–і—А–∞—В–∞ —Б–Њ —Б—В–Њ—А–Њ–љ–Њ–є, —А–∞–≤–љ–Њ–є –Њ–і–љ–Њ–є –µ–і–Є–љ–Є—Ж–µ, —А–∞–≤–љ–∞ –Ї–Њ—А–љ—О –Ї–≤–∞–і—А–∞—В–љ–Њ–Љ—Г –Є–Ј 2 (—А–Є—Б. 33). 
–Ґ–µ—А–Љ–Є–љ ¬Ђ–Ї–Њ—А–µ–љ—М¬ї –≤ –≤—Л—А–∞–ґ–µ–љ–Є–Є ¬Ђ–Ї–Њ—А–µ–љ—М –Ї–≤–∞–і—А–∞—В–љ—Л–є¬ї –Є–Љ–µ–µ—В –і—А–µ–≤–љ–µ–µ –њ—А–Њ–Є—Б—Е–Њ–ґ–і–µ–љ–Є–µ –Є –њ–Њ–і —А–∞–Ј—Г–Љ–µ–≤–∞–µ—В –њ–Њ–љ—П—В–Є–µ, –≤–Ј—П—В–Њ–µ –Є–Ј –њ—А–Є—А–Њ–і—Л. –Ъ–Њ—А–µ–љ—М —А–∞—Б—В–µ–љ–Є—П —Б–њ—А—П—В–∞–љ, –љ–Њ –њ–Њ—А–Њ–ґ–і–∞–µ—В –Є –њ–Є—В–∞–µ—В —В–Њ, —З—В–Њ –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Ґ–Њ—З–љ–Њ —В–∞–Ї –ґ–µ —Б–Ї—А—Л—В—Л –Є –Ї–Њ—А–љ–Є –Ї–≤–∞–і—А–∞—В–љ—Л—Е —З–Є—Б–µ–ї, –Є –≤—Б–µ –Њ–љ–Є –њ–Њ–і—А–∞–Ј—Г–Љ–µ–≤–∞—О—В—Б—П –≤ –љ–Є—Е. –Э–∞–њ—А–Є–Љ–µ—А, –Ї–Њ—А–µ–љ—М –Ї–≤–∞–і—А–∞—В–љ—Л–є –Є–Ј 16 —А–∞–≤–µ–љ 4 (4√Ч4=16). –Ъ–Њ—А–µ–љ—М –ґ–µ –Ї–≤–∞–і—А–∞—В–љ—Л–є –Є–Ј 15 –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є –Є—А—А–∞—Ж–Є–Њ–љ–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ, –Ї–Њ—В–Њ—А–Њ–µ –љ–µ —В–∞–Ї –ї–µ–≥–Ї–Њ –≤—Л—З–Є—Б–ї–Є—В—М. –Ш–Ј–≤–ї–µ—З–µ–љ–Є–µ –Ї–≤–∞–і—А–∞—В–љ—Л—Е –Ї–Њ—А–љ–µ–є –±—Л–ї–Њ –≥–ї–∞–≤–љ—Л–Љ –Ј–∞–љ—П—В–Є–µ–Љ –і—А–µ–≤–љ–Є—Е –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Њ–≤. –Ъ–Њ–≥–і–∞ –ґ–µ –Ї–Њ—А–µ–љ—М –Ї–≤–∞–і—А–∞—В–љ—Л–є –Ї–∞–Ї–Њ–≥–Њ-–ї–Є–±–Њ —З–Є—Б–ї–∞ –љ–µ–ї—М–Ј—П –±—Л–ї–Њ –Є–Ј–Њ–±—А–∞–Ј–Є—В—М –≤ —Ж–Є—Д—А–∞—Е, –µ–≥–Њ –≤—Б–µ–≥–і–∞ –Љ–Њ–ґ–љ–Њ –±—Л–ї–Њ –≤–Њ—Б–њ—А–Њ–Є–Ј–≤–µ—Б—В–Є –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є. –≠—В–Є–Љ –Є –Њ–±—К—П—Б–љ—П–µ—В—Б—П –≤–ї–∞—Б—В—М –≥–µ–Њ–Љ–µ—В—А–Є–Є –≤ –∞–љ—В–Є—З–љ–Њ–Љ –Љ–Є—А–µ. –У–µ–Њ–Љ–µ—В—А–Є—П —Б—З–Є—В–∞–ї–∞—Б—М –≤–Њ—А–Њ—В–∞–Љ–Є –≤ –≤—Л—Б—И–Є–µ —Б—Д–µ—А—Л —З–µ–ї–Њ–≤–µ—З–µ—Б–Ї–Њ–≥–Њ —Б–Њ–Ј–љ–∞–љ–Є—П, –Є –њ–Њ—Н—В–Њ–Љ—Г –µ–µ –њ—А–Є–љ—Ж–Є–њ—Л —Б—В–∞–ї–Є –≤–Ї–ї—О—З–∞—В—М—Б—П –≤ –Ї—Г–ї—М—В–Њ–≤–Њ–µ –Є—Б–Ї—Г—Б—Б—В–≤–Њ –Є –∞—А—Е–Є—В–µ–Ї—В—Г—А—Г. –Ю—В—В–∞–ї–Ї–Є–≤–∞—П—Б—М –Њ—В –њ—А–Њ–њ–Њ—А—Ж–Є–є —Б–≤—П—Й–µ–љ–љ–Њ–≥–Њ –Є—Б–Ї—Г—Б—Б—В–≤–∞ –Є –∞—А—Е–Є—В–µ–Ї—В—Г—А—Л, –Љ—Л –њ–Њ–ї—Г—З–∞–µ–Љ –Ї–Њ–љ—Ж–µ–њ—Ж–Є—О —Б–≤—П—Й–µ–љ–љ–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є–Є, –Ї–Њ—В–Њ—А—Г—О, –њ–Њ–ґ–∞–ї—Г–є, –ї—Г—З—И–µ –≤—Б–µ–≥–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М –Ї–∞–Ї –≥–µ–Њ–Љ–µ—В—А–Є—О, —Б–Ї—А—Л—В—Г—О –≤ —А–µ–ї–Є–≥–Є–Њ–Ј–љ—Л—Е –њ–Њ—Б—В—А–Њ–є–Ї–∞—Е –Є –і—Г—Е–Њ–≤–љ—Л—Е —Д–Њ—А–Љ–∞—Е. –Ы–µ–≥—З–µ –і—А—Г–≥–Є—Е –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е —Д–Њ—А–Љ –Є–Ј–Њ–±—А–∞–Ј–Є—В—М –Ї—А—Г–≥. –Ф–ї—П —Н—В–Њ–≥–Њ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ —Ж–Є—А–Ї—Г–ї—П –Є–ї–Є —И–љ—Г—А–Ї–∞, –Ї–Њ–ї—Л—И–Ї–∞ –Є –Љ–∞—А–Ї–µ—А–∞. –Ф–≤–∞ –≤–Ј–∞–Є–Љ–Њ—Б–≤—П–Ј–∞–љ–љ—Л—Е –Ї—А—Г–≥–∞ –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М, –њ–µ—А–µ–і–≤–Є–љ—Г–≤ –Ї–Њ–љ—З–Є–Ї —Ж–Є—А–Ї—Г–ї—П –љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –њ–µ—А–≤–Њ–≥–Њ –Ї—А—Г–≥–∞ –Є –љ–∞—А–Є—Б–Њ–≤–∞–≤ –≤—В–Њ—А–Њ–є —А–∞–≤–љ–Њ–≥–Њ —А–∞–Ј–Љ–µ—А–∞. –Т –Њ–±—А–∞–Ј–Њ–≤–∞–≤—И–µ–є—Б—П –≤–µ—Б–Є–Ї–µ –Љ–Њ–≥—Г—В –±—Л—В—М –њ–Њ–ї—Г—З–µ–љ—Л —В—А–Є —Б–∞–Љ—Л—Е –≤–∞–ґ–љ—Л—Е ¬Ђ–Ї–Њ—А–љ—П¬ї(вИЪ2, вИЪ3 –Є вИЪ5) (—А–Є—Б. 31). 
–Х—Б–ї–Є –њ—А–Є–љ—П—В—М —А–∞–і–Є—Г—Б –Ї—А—Г–≥–Њ–≤ –Ј–∞ 1, —В–Њ–≥–і–∞ –Ї–Њ—А–µ–љ—М –Ї–≤–∞–і—А–∞—В–љ—Л–є –Є–Ј –і–≤—Г—Е (вИЪ2) –Љ–Њ–ґ–µ—В –±—Л—В—М –њ–Њ–ї—Г—З–µ–љ –Є–Ј –і–Є–∞–≥–Њ–љ–∞–ї–Є –Ї–≤–∞–і—А–∞—В–∞, –Њ–±—А–∞–Ј–Њ–≤–∞–љ–љ–Њ–≥–Њ –ї–Є–љ–Є–µ–є –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П —Ж–µ–љ—В—А–∞–Љ–Є –Є –і–≤—Г–Љ—П –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л–Љ–Є –Ї –љ–µ–є —А–∞–і–Є—Г—Б–∞–Љ–Є. –Ъ–Њ—А–µ–љ—М –Ї–≤–∞–і—А–∞—В–љ—Л–є –Є–Ј —В—А–µ—Е (вИЪ3) –Њ–±—А–∞–Ј—Г–µ—В—Б—П –ї–Є–љ–Є–µ–є, —Б–Њ–µ–і–Є–љ—П—О—Й–µ–є –і–≤–µ —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –Ї—А—Г–≥–Њ–≤ –≤–µ—Б–Є–Ї–Є. –Ъ–Њ—А–µ–љ—М –Ї–≤–∞–і—А–∞—В–љ—Л–є –Є–Ј –њ—П—В–Є (вИЪ5) –і–∞–µ—В –і–Є–∞–≥–Њ–љ–∞–ї—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є 2 –Є 1. –≠—В–Њ—В –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї –Љ–Њ–ґ–љ–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –і–ї—П –Њ–±–љ–∞—А—Г–ґ–µ–љ–Є—П –Ј–Њ–ї–Њ—В–Њ–є –њ—А–Њ–њ–Њ—А—Ж–Є–Є (—Б–Љ. —А–Є—Б 35, –љ–∞ —А–Є—Б. 36, 37 –Є 38 –њ–Њ–Ї–∞–Ј–∞–љ—Л –і—А—Г–≥–Є–µ —Б–њ–Њ—Б–Њ–±—Л –њ–Њ–ї—Г—З–µ–љ–Є—П –Ј–Њ–ї–Њ—В–Њ–є –њ—А–Њ–њ–Њ—А—Ж–Є–Є). –Я–Њ–Ј–ґ–µ –Љ—Л —Г–≤–Є–і–Є–Љ, —З—В–Њ –≤–µ—Б–Є–Ї–∞ –Є –њ—А—П –Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є 2 –Є 1 —Б–ї—Г–ґ–Є–ї–Є –Ї–ї—О—З–Њ–Љ –Ї –њ–Њ–ї—Г—З–µ–љ–Є—О –і—А–µ–≤–љ–Є—Е –µ–і–Є–љ–Є—Ж –Є–Ј–Љ–µ—А–µ–љ–Є—П. –Ґ—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–ї—Б—П –Ї–∞–Ї –њ–µ—А–µ—Е–Њ–і–љ–∞—П —Д–Њ—А–Љ–∞ –Љ–µ–ґ–і—Г –Ї–≤–∞–і—А–∞—В–Њ–Љ –Є –Ї—А—Г–≥–Њ–Љ. –°–Њ –≤—А–µ–Љ–µ–љ–µ–Љ –Њ–љ —Б—В–∞–ї –Є–Ј–Њ–±—А–∞–ґ–∞—В—М —В—А–Є–∞–і—Г –±–Њ–≥–Њ–≤ –Є –±–Њ–≥–Є–љ—М, –Њ–±—Л—З–љ–Њ вАУ –Ї–∞–Ї –≤ –Х–≥–Є–њ—В–µ вАУ –Њ—В—Ж–∞, –Љ–∞—В—М –Є —Б—Л–љ–∞. –≠—В–∞ –Ї–Њ–љ—Ж–µ–њ—Ж–Є—П —Б–ї—Г–ґ–Є—В —Ж–µ–љ—В—А–∞–ї—М–љ—Л–Љ —Б—В–µ—А–ґ–љ–µ–Љ –Љ–љ–Њ–≥–Є—Е —А–µ–ї–Є–≥–Є–Њ–Ј–љ—Л—Е —Б–Є—Б—В–µ–Љ –Є –њ—А–Њ—П–≤–ї—П–µ—В —Б–µ–±—П –≤ —Е—А–Є—Б—В–Є–∞–љ—Б—В–≤–µ –≤ –≤–Є–і–µ –С–Њ–≥–∞ –Ю—В—Ж–∞, –°—Л–љ–∞ –Є –°–≤—П—В–Њ–≥–Њ –і—Г—Е–∞.  
–Ш–і–µ–∞–ї—М–љ—Л–Љ —Б—З–Є—В–∞–ї—Б—П —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, –≤ –Ї–Њ—В–Њ—А–Њ–Љ —А–∞–≤–љ—Л –≤—Б–µ —Б—В–Њ—А–Њ–љ—Л –Є —Г–≥–ї—Л. –®–Є—А–Њ–Ї–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї—Б—П –Є –і—А—Г–≥–Њ–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, –Њ–±—Л—З–љ–Њ –њ—А–Є–њ–Є—Б—Л–≤–∞–µ–Љ—Л–є –Я–Є—Д–∞–≥–Њ—А—Г, –љ–Њ —П–≤–љ–Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–≤—И–Є–є –Ј–∞–і–Њ–ї–≥–Њ –і–Њ –љ–µ–≥–Њ. –≠—В–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Є–Љ–µ–µ—В —Б—В–Њ—А–Њ–љ—Л, –≤—Л—А–∞–ґ–µ–љ–љ—Л–µ —Ж–µ–ї—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є 3: 4: 5. –Ю–љ —П–≤–ї—П–µ—В—Б—П –њ—А–Њ—Б—В–µ–є—И–Є–Љ –≤–∞—А–Є–∞–љ—В–Њ–Љ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ (90¬∞) —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є, –≤—Л—А–∞–ґ–∞–µ–Љ—Л–Љ–Є —Ж–µ–ї—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є. –С–ї–∞–≥–Њ–і–∞—А—П –њ—А–Њ—Б—В—Л–Љ –Њ—В–љ–Њ—И–µ–љ–Є—П–Љ —З–Є—Б–µ–ї –µ–≥–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Є –≤ —В–Њ–њ–Њ–≥—А–∞—Д–Є–Є, –∞ —В–∞–Ї–ґ–µ –≤ –Є—Б–Ї—Г—Б—Б—В–≤–µ –Є —Б–Ї—Г–ї—М–њ—В—Г—А–µ. –Э–∞ –љ–µ–Љ –Њ—Б–љ–Њ–≤–∞–љ–∞ –њ–Є—А–∞–Љ–Є–і–∞ –•–∞—Д—А—Л. –Ъ—А—Г–≥, —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, –Ї–≤–∞–і—А–∞—В –Є –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї –Њ–±—А–∞–Ј—Г—О—В –Њ—Б–љ–Њ–≤—Г –Ї—Г–ї—М—В–Њ–≤–Њ–є –∞—А—Е–Є—В–µ–Ї—В—Г—А—Л. –Ю–љ–Є —В—А–∞–і–Є—Ж–Є–Њ–љ–љ–Њ –±—Л–ї–Є —Б–≤—П–Ј–∞–љ—Л –і—А—Г–≥ —Б –і—А—Г–≥–Њ–Љ –Њ—Б–Њ–±—Л–Љ–Є –њ—А–Њ–њ–Њ—А—Ж–Є—П–Љ–Є. –Я–Њ—Б–ї–µ–і–љ–Є–µ –њ—А–Є–Ј–≤–∞–љ—Л –±—Л–ї–Є –Њ—В–Њ–±—А–∞–Ј–Є—В—М —Б–Њ–±—Б—В–≤–µ–љ–љ—Г—О –≥–∞—А–Љ–Њ–љ–Є—О –Ї–Њ—Б–Љ–Њ—Б–∞. 
–Ю–і–љ–∞ —В–∞–Ї–∞—П –њ—А–Њ–њ–Њ—А—Ж–Є—П вАУ ¬Ђ–≥–љ–Њ–Љ–Њ–љ¬ї –±—Л–ї–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ –Р—А–Є—Б—В–Њ—В–µ–ї–µ–Љ —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ: ¬Ђ–Ы—О–±–∞—П —Д–Є–≥—Г—А–∞, –Ї–Њ—В–Њ—А–∞—П, –±—Г–і—Г—З–Є –і–Њ–±–∞–≤–ї–µ–љ–љ–Њ–є –Ї –Є—Б–Ї–Њ–љ–љ–Њ–є —Д–Є–≥—Г—А–µ, –і–∞–µ—В –≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ —Д–Є–≥—Г—А—Г, –њ–Њ–і–Њ–±–љ—Г—О –Є—Б–Ї–Њ–љ–љ–Њ–є¬ї. –Ш–љ—Л–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, —Б–Њ—Е—А–∞–љ—П—О—В—Б—П —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–µ–ґ–і—Г –≤—Б–µ–Љ–Є –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–Љ–Є —И–∞–≥–∞–Љ–Є. –Я—А–Є–Љ–µ—А–Њ–Љ —Н—В–Њ–≥–Њ —Б–ї—Г–ґ–Є—В –Ј–Њ–ї–Њ—В–Њ–µ —Б–µ—З–µ–љ–Є–µ, –Ї–Њ—В–Њ—А–Њ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –≤—Л—А–∞–ґ–µ–љ–Њ —З–Є—Б–ї–∞–Љ–Є 1, 1, 2, 3, 5, 8, 13, 23 –Є —В –і., –≥–і–µ –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–µ–ґ–і—Г –ї—О–±—Л–Љ–Є –і–≤—Г–Љ—П —Б–Њ—Б–µ–і–љ–Є–Љ–Є —З–Є—Б–ї–∞–Љ–Є –±—Л—Б—В—А–Њ —Б—Е–Њ–і—П—В—Б—П –≤ –Њ–і–љ–Њ–є —В–Њ—З–Ї–µ –њ–Њ –Љ–µ—А–µ –і–≤–Є–ґ–µ–љ–Є—П –њ–Њ —А—П–і—Г. –†—П–і –§–Є–±–Њ–љ–∞—З—З–Є —П–≤–ї—П–µ—В—Б—П —Б–∞–Љ—Л–Љ –Є–Ј–≤–µ—Б—В–љ—Л–Љ –њ—А–Є–Љ–µ—А–Њ–Љ –≥–љ–Њ–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ—В–љ–Њ—И–µ–љ–Є—П, –љ–Њ –µ—Б—В—М –Є –і—А—Г–≥–Є–µ.  –†–Є—Б. 39. –У–љ–Њ–Љ–Њ–љ–Є—З–µ—Б–ґ–Є–µ —Б–њ–Є—А–∞–ї–Є, –њ–Њ—Б—В—А–Њ–µ–љ–љ—Л–µ –Є–Ј –Њ—В–љ–Њ—И–µ–љ–Є—П –Ї–≤–∞–і—А–∞—В–∞ 2:1
–Т —Б–≤–Њ–µ–є –Ї–љ–Є–≥–µ ¬Ђ–°–≤—П—Й–µ–љ–љ–∞—П –≥–µ–Њ–Љ–µ—В—А–Є—П¬ї –†–Њ–±–µ—А—В –Ы–Њ–ї–Њ—А –њ—А–Є–≤–Њ–і–Є—В –њ—А–Є–Љ–µ—А—Л ¬Ђ–≥–љ–Њ–Љ–Њ–љ–Є—З–µ—Б–Ї–Є—Е¬ї —Б–њ–Є—А–∞–ї–µ–є, –њ–Њ–і–Њ–±–љ—Л—Е –Њ—Б–љ–Њ–≤–∞–љ–љ–Њ–є –љ–∞ —А—П–і–µ –§–Є–±–Њ–љ–∞—З—З–Є, –њ–Њ–ї—Г—З–µ–љ–љ–Њ–є –Є–Ј –Њ—В–љ–Њ—И–µ–љ–Є—П 1:2. –≠—В–Є —А–∞—Б—И–Є—А—П—О—Й–Є–µ—Б—П —Б—Е–µ–Љ—Л –Є–љ–Њ–≥–і–∞ –љ–∞–Ј—Л–≤–∞—О—В ¬Ђ–Ј–∞–≤–Є—Е—А–µ–љ–љ—Л–Љ–Є –Ї–≤–∞–і—А–∞—В–∞–Љ–Є¬ї, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –Њ–љ–Є –і–∞—О—В —Б–њ–Є—А–∞–ї–Є, –Ї–Њ—В–Њ—А—Л–µ —З–∞—Б—В–Њ –≤—Б—В—А–µ—З–∞—О—В—Б—П –≤ –њ—А–Є—А–Њ–і–µ (—А–Є—Б. 39). –Ш–Ј—Г—З–∞—П ¬Ђ–≥–љ–Њ–Љ–Њ–љ—Л¬ї —Б —А–∞–Ј–љ—Л–Љ–Є –Њ—В–љ–Њ—И–µ–љ–Є—П–Љ–Є, —П —Б–і–µ–ї–∞–ї –≤–∞–ґ–љ–Њ–µ –Њ—В–Ї—А—Л—В–Є–µ ¬Ђ–У–љ–Њ–Љ–Њ–љ¬ї, –Њ—Б–љ–Њ–≤–∞–љ–љ—Л–є –љ–∞ –Њ—В–љ–Њ—И–µ–љ–Є–Є 1:3, –Є–Љ–µ–µ—В –љ–µ–њ–Њ—Б—А–µ–і—Б—В–≤–µ–љ–љ–Њ–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –Ї –њ–Є—А–∞–Љ–Є–і–∞–Љ –У–Є–Ј—Л. –Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ –Є–Ј —Н—В–Њ–≥–Њ –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–Њ–≥—Г—В –±—Л—В—М –њ–Њ–ї—Г—З–µ–љ—Л –Њ—Б–љ–Њ–≤–љ—Л–µ –њ—А–Њ–њ–Њ—А—Ж–Є–Є –њ–Є—А–∞–Љ–Є–і –•—Г—Д—Г, –•–∞—Д—А—Л –Є –Ь–µ–љ–Ї–∞—Г—А–∞ (—А–Є—Б. 40). –Т—Б–µ –љ–∞—З–Є–љ–∞–µ—В—Б—П —Б —В—А–µ—Е –Ї–≤–∞–і—А–∞—В–Њ–≤, —Б–Њ–µ–і–Є–љ–µ–љ–љ—Л—Е –≤ –ї–Є–љ–Є—О –Є –Њ–±—А–∞–Ј—Г—О—Й–Є—Е –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є 3 –Є 1. –Ч–∞—В–µ–Љ —З–µ—А—В–Є—В—Б—П –Ї–≤–∞–і—А–∞—В –љ–∞ –і–ї–Є–љ–љ–Њ–є —Б—В–Њ—А–Њ–љ–µ –љ–∞ –Ї–∞–ґ–і–Њ–Љ —Н—В–∞–њ–µ —Г–≤–µ–ї–Є—З–µ–љ–Є—П. –Я–µ—А–≤—Л–є –Ї–≤–∞–і—А–∞—В –Њ–±—А–∞–Ј—Г–µ—В –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї —Б –Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ —Б—В–Њ—А–Њ–љ 3:4. –Я—А–Є –µ–≥–Њ —Г–і–≤–Њ–µ–љ–Є–Є –њ–Њ–ї—Г—З–∞–µ—В—Б—П –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–Є—А–∞–Љ–Є–і—Л –•–∞—Д—А—Л вАУ 6:4. –Я—А–Є –і–Њ–±–∞–≤–ї–µ–љ–Є–Є –µ—Й–µ –і–≤—Г—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л—Е –Ї–≤–∞–і—А–∞—В–Њ–≤ –Ї –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї—Г 3:4 –њ–Њ–ї—Г—З–∞–µ–Љ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–Є—А–∞–Љ–Є–і—Л –•—Г—Д—Г вАУ 7:11. –Х—Й–µ –Њ–і–Є–љ –і–Њ–±–∞–≤–ї–µ–љ–љ—Л–є –Ї–≤–∞–і—А–∞—В –і–∞–µ—В –њ—А–Њ–њ–Њ—А—Ж–Є–Є –њ–Є—А–∞–Љ–Є–і—Л –Ь–µ–љ–Ї–∞—Г—А–∞ вАУ 11:18. –≠—В–Њ—В –њ—А–Є–µ–Љ –і–Њ–±–∞–≤–ї–µ–љ–Є—П –Ї–≤–∞–і—А–∞—В–Њ–≤ –Ї –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї—Г 3:1 –і—А–∞–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –Њ–±–љ–∞—А—Г–ґ–Є–≤–∞–µ—В, —З—В–Њ –њ–Є—А–∞–Љ–Є–і—Л –Њ—В—А–∞–ґ–∞—О—В –µ—Б—В–µ—Б—В–≤–µ–љ–љ—Г—О –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї—Г—О –њ—А–Њ–≥—А–µ—Б—Б–Є—О –≤ –Њ—В–љ–Њ—И–µ–љ–Є—П—Е –Є—Е –≤—Л—Б–Њ—В—Л –Ї –Њ—Б–љ–Њ–≤–∞–љ–Є—О. –Ґ–∞–Ї –Є–ї–Є –Є–љ–∞—З–µ, –љ–Њ –Њ–љ–Є —Б–≤—П–Ј–∞–љ—Л –≥–∞—А–Љ–Њ–љ–Є—З–љ—Л–Љ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–Љ —А—П–і–Њ–Љ. 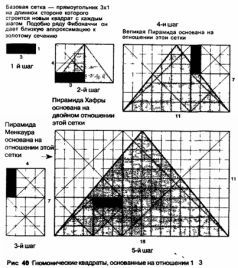
–І—В–Њ –њ—А–Є–Љ–µ—З–∞—В–µ–ї—М–љ–Њ–≥–Њ –Љ–Њ–≥–ї–Њ –±—Л—В—М –≤ –Њ—В–љ–Њ—И–µ–љ–Є–Є 3:1? –Ь–Њ–ґ–µ—В –±—Л—В—М, –Њ–љ–Њ –Њ—В—А–∞–ґ–∞–ї–Њ —Б–Є–Љ–≤–Њ–ї–Є–Ј–Љ –µ–≥–Є–њ–µ—В—Б–Ї–Њ–є —В—А–Њ–Є—Ж—Л вАУ –Ю—Б–Є—А–Є—Б–∞, –Ш—Б–Є–і—Л –Є –У–Њ—А–∞. –Т–Њ–Ј–Љ–Њ–ґ–љ–Њ, –Љ—Л –љ–Є–Ї–Њ–≥–і–∞ —Н—В–Њ–≥–Њ –љ–µ —Г–Ј–љ–∞–µ–Љ –љ–∞–≤–µ—А–љ—П–Ї–∞, –љ–Њ —Н—В–Њ—В —А–Є—Б—Г–љ–Њ–Ї –њ–Њ–Ј–≤–Њ–ї—П–µ—В –љ–∞–Љ –ї—Г—З—И–µ –њ–Њ–љ—П—В—М –Љ–µ—В–Њ–і—Л –µ–≥–Є–њ—В—П–љ. –≠—В–Њ –Њ—В–Ї—А—Л—В–Є–µ —Б–Њ–≥–ї–∞—Б—Г–µ—В—Б—П —Б —В–µ–Љ, —З—В–Њ –љ–∞–Љ –Є–Ј–≤–µ—Б—В–љ–Њ –Њ –µ–≥–Є–њ–µ—В—Б–Ї–Є—Е –Љ–µ—В–Њ–і–∞—Е –њ—А–Њ–µ–Ї—В–Є—А–Њ–≤–∞–љ–Є—П, –Ї–Њ—В–Њ—А—Л–µ, –њ–Њ—Е–Њ–ґ–µ, –≤—Б–µ–≥–і–∞ –Њ—Б–љ–Њ–≤—Л–≤–∞–ї–Є—Б—М –љ–∞ —Б—Е–µ–Љ–∞—Е –Ї–≤–∞–і—А–∞—В–љ–Њ–є —Б–µ—В–Ї–Є. –Т –µ–≥–Є–њ–µ—В—Б–Ї–Њ–Љ –Є—Б–Ї—Г—Б—Б—В–≤–µ –Є–Љ–µ—О—В—Б—П –Љ–љ–Њ–≥–Њ—З–Є—Б–ї–µ–љ–љ—Л–µ –њ—А–Є–Љ–µ—А—Л, –њ–Њ–Ї–∞–Ј—Л–≤–∞—О—Й–Є–µ, —З—В–Њ —Е—Г–і–Њ–ґ–љ–Є–Ї–Є –Є —Б–Ї—Г–ї—М–њ—В–Њ—А—Л —Б–љ–∞—З–∞–ї–∞ —А–Є—Б–Њ–≤–∞–ї–Є —Б–µ—В–Ї—Г –љ–∞ —Б—В–µ–љ–µ, –Ї–Њ—В–Њ—А—Г—О –њ—А–µ–і—Б—В–Њ—П–ї–Њ —А–∞—Б–њ–Є—Б–∞—В—М –Є–ї–Є –≤—Л—А–µ–Ј–∞—В—М, –і–ї—П —В–Њ–≥–Њ —З—В–Њ–±—Л —Б–Њ—Е—А–∞–љ–Є—В—М —Г—Б—В–∞–љ–Њ–≤–ї–µ–љ–љ—Л–µ –њ—А–Њ–њ–Њ—А—Ж–Є–Є. –Я—А–Њ—Б—В—Л–µ —З–Є—Б–ї–Њ–≤—Л–µ –Њ—В–љ–Њ—И–µ–љ–Є—П —Н—В–Є—Е —Б–µ—В–Њ–Ї —Б–ї—Г–ґ–∞—В —Б–µ—А–і—Ж–µ–≤–Є–љ–Њ–є –≤—Б–µ—Е –≤–µ–ї–Є–Ї–Є—Е —Е—Г–і–Њ–ґ–µ—Б—В–≤–µ–љ–љ—Л—Е –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–є –µ–≥–Є–њ—В—П–љ. –Ґ–Њ—В –ґ–µ –Љ–µ—В–Њ–і –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї—Б—П –Љ–љ–Њ–≥–Є–Љ–Є —Е—Г–і–Њ–ґ–љ–Є–Ї–∞–Љ–Є –Т–Њ–Ј—А–Њ–ґ–і–µ–љ–Є—П, –≤ —В–Њ–Љ —З–Є—Б–ї–µ –Є –Ы–µ–Њ–љ–∞—А–і–Њ –і–∞ –Т–Є–љ—З–Є. –Т –Ф—А–µ–≤–љ–µ–Љ –Х–≥–Є–њ—В–µ —Н—В–Њ –љ–∞—И–ї–Њ —Б–≤–Њ–µ–≤–Њ–њ–ї–Њ—Й–µ–љ–Є–µ –≤ –Т–µ–ї–Є–Ї–Њ–є –њ–Є—А–∞–Љ–Є–і–µ, —З—В–Њ –Є –њ–Њ–і–Ї—А–µ–њ–ї—П–µ—В—Б—П –µ–µ —В–µ—Б–љ–Њ–є —Б–≤—П–Ј—М—О —Б —Г–Ј–Њ—А–Њ–Љ –љ–∞ –Ь–∞—А–ї–±–Њ—А–Њ-–Ф–∞—Г–љ—Б. –Э–∞ –Ь–∞—А–ї–±–Њ—А–Њ-–Ф–∞—Г–љ—Б —А–∞–Ј–Љ–µ—Й–µ–љ—Л –і–≤–∞ –≤–Ј–∞–Є–Љ–Њ—Б–≤—П–Ј–∞–љ–љ—Л—Е –Ї—А—Г–≥–∞, –Ї–∞–ґ–і—Л–є –і–Є–∞–Љ–µ—В—А–Њ–Љ –≤ 19,3 –Ї–Є–ї–Њ–Љ–µ—В—А–∞ (12 –Љ–Є–ї—М). –Т –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ –Ї—А—Г–≥–Є –љ–µ –Њ–±—А–∞–Ј—Г—О—В –њ–Њ–і–ї–Є–љ–љ—Л–є —Г–Ј–Њ—А –≤–µ—Б–Є–Ї–Є –Є –њ–Њ—Н—В–Њ–Љ—Г –љ–µ –Є–Љ–µ—О—В —П–≤–љ–Њ–≥–Њ –Њ—В–љ–Њ—И–µ–љ–Є—П –Ї –Є–Ј–≤–µ—Б—В–љ—Л–Љ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–Љ —Д–Є–≥—Г—А–∞–Љ. –Ъ–∞–Ї –Љ–љ–µ –њ—А–µ–і—Б—В–Њ—П–ї–Њ —Б–Њ –≤—А–µ–Љ–µ–љ–µ–Љ –Њ—В–Ї—А—Л—В—М, —А–∞–Ј–Љ–µ—Й–µ–љ–Є–µ —Н—В–Є—Е –Ї—А—Г–≥–Њ–≤ –љ–µ –±—Л–ї–Њ –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Л–Љ, –∞ –њ–Њ–і—З–Є–љ—П–ї–Њ—Б—М –Њ—Б–Њ–±–Њ–Љ—Г –Њ—В–љ–Њ—И–µ–љ–Є—О, –љ–∞–є–і–µ–љ–љ–Њ–Љ—Г –≤ –Т–µ–ї–Є–Ї–Њ–є –њ–Є—А–∞–Љ–Є–і–µ –•—Г—Д—Г. –Я—А–Є –љ–∞–ї–Њ–ґ–µ–љ–Є–Є –њ–Њ–њ–µ—А–µ—З–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П –Т–µ–ї–Є–Ї–Њ–є –њ–Є—А–∞–Љ–Є–і—Л –љ–∞ –Ї–∞—А—В—Г (—А–Є—Б. 21) –Њ–±–љ–∞—А—Г–ґ–Є–≤–∞–µ—В—Б—П –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ –Њ–±—К—П—Б–љ–µ–љ–Є–µ –ї–Є–љ–µ–є–љ–Њ–≥–Њ –њ–Њ—Б—В—А–Њ–µ–љ–Є—П –≥–∞–ї–µ—А–µ–є, —Е–Њ–і–Њ–≤ –Є –Ї–∞–Љ–µ—А –њ–Є—А–∞–Љ–Є–і—Л, –≤ —З–∞—Б—В–љ–Њ—Б—В–Є, –Њ—А–Є–µ–љ—В–∞—Ж–Є–Є –С–Њ–ї—М—И–Њ–є –≥–∞–ї–µ—А–µ–Є –њ–Є—А–∞–Љ–Є–і—Л –љ–∞ —Ж–µ–љ—В—А –Њ–і–љ–Њ–≥–Њ –Є–Ј –Ї—А—Г–≥–Њ–≤. –≠—В–Њ –њ–Њ–Ј–≤–Њ–ї—П–ї–Њ –Њ–±—К—П—Б–љ–Є—В—М –Љ–µ—Б—В–Њ–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –Є —А–∞–Ј–Љ–µ—А—Л –≤—Б–µ—Е –≤–љ—Г—В—А–µ–љ–љ–Є—Е –Ї–∞–Љ–µ—А –Є –≥–∞–ї–µ—А–µ–є –Т–µ–ї–Є–Ї–Њ–є –њ–Є—А–∞–Љ–Є–і—Л –љ–∞ —П–Ј—Л–Ї–µ —З–Є—Б—В–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є–Є –Є –Њ—В–Ї—А—Л–≤–∞–ї–Њ –≤–Њ–ї–љ—Г—О—Й—Г—О –њ–µ—А—Б–њ–µ–Ї—В–Є–≤—Г. –Ф–ї—П —А–∞–Ј–≥–∞–і–Ї–Є —Н—В–Њ–є —В–∞–є–љ—Л –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –±—Л–ї–Њ –≤—Л —П—Б–љ–Є—В—М, –Ї–∞–Ї –µ–≥–Є–њ—В—П–љ–µ –Љ–Њ–≥–ї–Є –њ—А–Є–є—В–Є –Ї –њ—А–Њ–µ–Ї—В—Г –Т–µ–ї–Є–Ї–Њ–є –њ–Є—А–∞–Љ–Є–і—Л —Б –њ–Њ–Љ–Њ—Й—М—О —З–Є—Б—В–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є–Є –њ—А–µ–ґ–і–µ, —З–µ–Љ –њ—А–Є—Б–њ–Њ—Б–Њ–±–Є—В—М –µ–≥–Њ –Ї —Б–µ—В–Ї–µ 7:11. –Т —А–Є—Б—Г–љ–Ї–µ –Ь–∞—А–ї–±–Њ—А–Њ-–Ф–∞—Г–љ—Б –Ї–ї—О—З–Њ–Љ —Б–ї—Г–ґ–Є–ї —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї. –Т–Ј—П–≤ –µ–≥–Њ –Ј–∞ –Њ—Б–љ–Њ–≤—Г, —Б–≤–Њ–є—Б—В–≤–µ–љ–љ—Г—О –њ–Є—А–∞–Љ–Є–і–µ –•—Г—Д—Г, –≥–µ–Њ–Љ–µ—В—А–Є—О –Љ–Њ–ґ–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М —Б –њ–Њ–Љ–Њ—Й—М—О —А–Є—Б—Г–љ–Ї–Њ–≤ 41-46. –Ґ–∞–Ї–Њ–є –њ–Њ—Н—В–∞–њ–љ—Л–є —З–µ—А—В–µ–ґ —Д–Є–Ї—Б–Є—А—Г–µ—В –Љ–µ—Б—В–Њ–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –≤—Б–µ—Е –Ї–∞–Љ–µ—А –Є —Е–Њ–і–Њ–≤ –Т–µ–ї–Є–Ї–Њ–є –њ–Є—А–∞–Љ–Є–і—Л. –Ю–і–љ–∞–Ї–Њ —З–Є—Б—В–∞—П –≥–µ–Њ–Љ–µ—В—А–Є—П —Б–Њ–Ј–і–∞–µ—В –Є—А—А–∞—Ж–Є–Њ–љ–∞–ї—М–љ—Л–µ –њ—А–Њ–њ–Њ—А—Ж–Є–Є. –£—Б—В–∞–љ–Њ–≤–Є–≤ –±–∞–Ј–Њ–≤—Г—О —Б—В—А—Г–Ї—В—Г—А—Г, –і–∞–ї—М—И–µ —Б–ї–µ–і–Њ–≤–∞–ї–Њ –њ—А–µ–≤—А–∞—В–Є—В—М –µ–µ –≤ —В–∞–Ї—Г—О —Д–Њ—А–Љ—Г, –Ї–Њ—В–Њ—А—Г—О –Љ–Њ–ґ–љ–Њ –±—Л–ї–Њ –±—Л –≤—Л—А–∞–Ј–Є—В—М —А–∞—Ж–Є–Њ–љ–∞–ї—М–љ—Л–Љ–Є –Є–ї–Є —Ж–µ–ї—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є. –Т —Н—В–Њ–Љ –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –±–Њ–ї—М—И–∞—П —Ж–µ–љ–љ–Њ—Б—В—М —Б–µ—В–Ї–Є. –Я—А–Є –µ–µ –љ–∞–ї–Њ–ґ–µ–љ–Є–Є –љ–∞ –≥–µ–Њ–Љ–µ—В—А–Є—О –Љ–Њ–≥—Г—В –±—Л—В—М —Б—З–Є—В–∞–љ—Л —В–Њ—З–љ—Л–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П. –Ь–Њ–ґ–љ–Њ —Б–і–µ–ї–∞—В—М –≤—Л–≤–Њ–і, —З—В–Њ –Є–Љ–µ–љ–љ–Њ —В–∞–Ї –±—Л–ї–∞ —Б–њ—А–Њ–µ–Ї—В–Є—А–Њ–≤–∞–љ–∞ –Т–µ–ї–Є–Ї–∞—П –њ–Є—А–∞–Љ–Є–і–∞, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г —З–Є—Б—В–∞—П –≥–µ–Њ–Љ–µ—В—А–Є—П –і–Њ–ї–ґ–љ–∞ –±—Л–ї–∞ –і–∞—В—М —Г–≥–Њ–ї —Б–Ї–ї–Њ–љ–∞ —З—Г—В—М –Љ–µ–љ—М—И–µ, —З–µ–Љ –Љ—Л –≤–Є–і–Є–Љ –љ–∞ –њ—А–∞–Ї—В–Є–Ї–µ. –Я—А–Є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–Є —Б–µ—В–Ї–Є —Б —В–Њ—З–љ–Њ–є –њ—А–Њ–њ–Њ—А—Ж–Є–µ–є 7:11 –≤—Б–µ –∞–Ї–Ї—Г—А–∞—В–љ–Њ —Б—В–∞–љ–Њ–≤–Є—В—Б—П –љ–∞ –Љ–µ—Б—В–Њ –Є –і–Њ—Б—В–Є–≥–∞–µ—В—Б—П –Є–і–µ–∞–ї—М–љ—Л–є –Ї–Њ–Љ–њ—А–Њ–Љ–Є—Б—Б –Љ–µ–ґ–і—Г —З–Є—Б—В–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є–µ–є –Є –µ–µ –≥–∞—А–Љ–Њ–љ–Є—З–љ—Л–Љ –≤—Л—А–∞–ґ–µ–љ–Є–µ–Љ –≤ –Љ–Є—А–µ —Д–Њ—А–Љ—Л. –Э–∞–ї–Њ–ґ–µ–љ–Є–µ —Б–µ—В–Ї–Є 7:11 –љ–∞ –њ–Є—А–∞–Љ–Є–і—Г –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –Ї–∞–Љ–µ—А–∞ –¶–∞—А—П —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–∞ –љ–∞ –і–≤–∞ –Ї–≤–∞–і—А–∞—В–∞ (–љ–∞ 2/7 –µ–µ –≤—Л—Б–Њ—В—Л) –≤—Л—И–µ —Г—А–Њ–≤–љ—П –Ј–µ–Љ–ї–Є, –∞ –Ї–∞–Љ–µ—А–∞ –¶–∞—А–Є—Ж—Л вАУ –љ–∞ –Њ–і–Є–љ –Ї–≤–∞–і—А–∞—В –≤—Л—И–µ —Г—А–Њ–≤–љ—П –Ј–µ–Љ–ї–Є, —В–Њ –µ—Б—В—М –љ–∞ 1/7 –≤—Л—Б–Њ—В—Л –њ–Є—А–∞–Љ–Є–і—Л (—А–Є—Б. 47). –Т—Е–Њ–і –≤ –њ–Є—А–∞–Љ–Є–і—Г, –љ–∞ –Љ–Њ–є –≤–Ј–≥–ї—П–і, –±—Л–ї —А–∞—Б—Б—З–Є—В–∞–љ –љ–∞ –Њ—Б–љ–Њ–≤–µ –њ–Њ–і–µ–ї–µ–љ–љ–Њ–≥–Њ –њ–Њ–њ–Њ–ї–∞–Љ –Ї–≤–∞–і—А–∞–љ—В–∞ –њ–µ—А–≤–Њ–≥–Њ –Ї–≤–∞–і—А–∞—В–∞ –≤ —В–Њ–Љ –Љ–µ—Б—В–µ, –≥–і–µ –Њ–љ –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Г –њ–Є—А–∞–Љ–Є–і—Л.  
–£–≥–ї—Л –љ–∞–Ї–ї–Њ–љ–∞ –≤–Њ—Б—Е–Њ–і—П—Й–µ–≥–Њ –Є –љ–Є—Б—Е–Њ–і—П—Й–µ–≥–Њ —Е–Њ–і–Њ–≤ —А–∞–≤–љ—Л 26¬Ї31'23¬ї. –Э–∞ –њ–µ—А–≤—Л–є –≤–Ј–≥–ї—П–і, –Њ–љ –Ї–∞–ґ–µ—В—Б—П –≤–µ—Б—М–Љ–∞ —Б—В—А–∞–љ–љ—Л–Љ, –љ–Њ –љ–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ —П–≤–ї—П–µ—В—Б—П –њ—А–Њ—Б—В—Л–Љ –≥—А–∞–і–Є–µ–љ—В–Њ–Љ, –Њ–±—А–∞–Ј–Њ–≤–∞–љ–љ—Л–Љ –Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ 2:1. –Ш–љ—Л–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, —Е–Њ–і –њ–Њ–і–љ–Є–Љ–∞–µ—В—Б—П –љ–∞ –Њ–і–Є–љ –Ї–≤–∞–і—А–∞—В –њ—А–Є –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ–Њ–Љ –њ–µ—А–µ–Љ–µ—Й–µ–љ–Є–Є –љ–∞ –Ї–∞–ґ–і—Л–µ –і–≤–∞ –Ї–≤–∞–і—А–∞—В–∞, –Њ–±—А–∞–Ј—Г—П –і–Є–∞–≥–Њ–љ–∞–ї—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —Б –Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ —Б—В–Њ—А–Њ–љ 2:1. –Х–≥–Њ –Љ–Њ–ґ–љ–Њ –±—Л–ї–Њ –ї–µ–≥–Ї–Њ –њ–Њ—Б—В—А–Њ–Є—В—М, –Є –µ–≥–Њ, –±–µ–Ј —Б–Њ–Љ–љ–µ–љ–Є—П, –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Є –±–ї–∞–≥–Њ–і–∞—А—П –Љ–µ—Б—В—Г —Н—В–Њ–≥–Њ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –≤ —Б–≤—П—Й–µ–љ–љ–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є–Є, –≤ —З–∞—Б—В–љ–Њ—Б—В–Є, –≤ –њ–Њ–ї—Г—З–µ–љ–Є–Є –Ј–Њ–ї–Њ—В–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П. –Х—Б–ї–Є –њ—А–Є–±–µ–≥–љ—Г—В—М –Ї —Н—В–Є–Љ –Љ–µ—В–Њ–і–∞–Љ, —В–Њ –Љ–Њ–ґ–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –≤—Б–µ –≤–љ—Г—В—А–µ–љ–љ–Є–µ —Е–Њ–і—Л –Є –њ–Њ–Ї–Њ–Є –Њ—Б–љ–Њ–≤–∞–љ—Л –љ–∞ –њ—А–Њ—Б—В—Л—Е –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е –њ—А–Њ–њ–Њ—А—Ж–Є—П—Е, —Е–Њ—В—П —В–∞–Ї –љ–∞–Ј—Л–≤–∞–µ–Љ—Л–µ –≤–µ–љ—В–Є–ї—П—Ж–Є–Њ–љ–љ—Л–µ —И–∞—Е—В—Л –љ–µ —Б–Њ–≤—Б–µ–Љ —Б–Њ–≤–њ–∞–і–∞—О—В —Б —Н—В–Њ–є —Б—Е–µ–Љ–Њ–є. –≠—В–Њ –љ–∞–≤–Њ–і–Є—В –љ–∞ –Љ—Л—Б–ї—М –Њ —В–Њ–Љ, —З—В–Њ –Њ–љ–Є –±—Л–ї–Є —Б–Њ–Ј–і–∞–љ—Л —Б –∞—Б—В—А–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Є–Љ–Є —Ж–µ–ї—П–Љ–Є, –Ї–∞–Ї —Н—В–Њ –Є –њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є–ї–Є –С—М—О–≤—Н–ї –Є –Ф–ґ–Є–ї–±–µ—А—В –≤ ¬Ђ–Ґ–∞–є–љ–µ –Ю—А–Є–Њ–љ–∞¬ї. –Ъ–∞–Ї —В–Њ–ї—М–Ї–Њ –±—Л–ї–Є —Г—Б—В–∞–љ–Њ–≤–ї–µ–љ—Л –њ–µ—А–≤–Є—З–љ—Л–µ –њ–∞—А–∞–Љ–µ—В—А—Л —Б–µ—В–Ї–Є, –љ–µ —Б–Њ—Б—В–∞–≤–Є–ї–Њ —В—А—Г–і–∞ —Б–Њ–Њ—А—Г–і–Є—В—М —Г–≥–ї–Њ–≤—Л–µ —И–∞–±–ї–Њ–љ—Л, –Ї–Њ—В–Њ—А—Л–µ –Њ–±–µ—Б–њ–µ—З–Є–≤–∞–ї–Є —Б –њ–Њ–Љ–Њ—Й—М—О –Њ—В–≤–µ—Б–∞ –≤—Л—Б–Њ–Ї—Г—О —В–Њ—З–љ–Њ—Б—В—М –≥—А–∞–і–Є–µ–љ—В–Њ–≤ —А–∞–Ј–ї–Є—З–љ—Л—Е —Е–Њ–і–Њ–≤. –Х–≥–Є–њ—В–Њ–ї–Њ–≥–Є –њ–Њ—Б—В–Њ—П–љ–љ–Њ —В–≤–µ—А–і–Є–ї–Є, —З—В–Њ –≤ —А–∞–Ј–Љ–µ—Й–µ–љ–Є–Є –њ–Є—А–∞–Љ–Є–і –љ–∞ –њ–ї–∞—В–Њ –У–Є–Ј–∞ –љ–µ—В –µ–і–Є–љ–Њ–≥–Њ –њ–ї–∞–љ–∞. –Э–µ –њ–Њ–љ–Є–Љ–∞—О, –Ї–∞–Ї –Њ–љ–Є —Г–Љ—Г–і—А–Є–ї–Є—Б—М –њ—А–Є–є—В–Є –Ї —В–∞–Ї–Њ–Љ—Г –≤—Л–≤–Њ–і—Г. –Ф–Њ—Б—В–∞—В–Њ—З–љ–Њ –њ—А–Є–ї–Њ–ґ–Є—В—М –Є–Ј–≤–µ—Б—В–љ—Л–µ –њ—А–Є–љ—Ж–Є–њ—Л –і—А–µ–≤–љ–µ–µ–≥–Є–њ–µ—В—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л –Љ–µ—А –Ї –њ–ї–∞—В–Њ –У–Є–Ј–∞, —З—В–Њ–±—Л –њ–Њ–љ—П—В—М –ї–µ–ґ–∞—Й—Г—О –≤ –µ–≥–Њ –Њ—Б–љ–Њ–≤–µ —Б—Е–µ–Љ—Г. –Х–≥–Є–њ—В—П–љ–µ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Є –Є–Љ–µ–љ–љ–Њ —Б–µ—В—З–∞—В—Г—О —Б–Є—Б—В–µ–Љ—Г. –Ь–љ–µ –Њ—Б—В–∞–≤–∞–ї–Њ—Б—М –ї–Є—И—М –љ–∞–є—В–Є —Б–µ—В–Ї—Г, –Ї–Њ—В–Њ—А–∞—П –љ–∞–Є–ї—Г—З—И–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Њ–≤–∞–ї–∞ –±—Л –Ї–Њ–Љ–њ–ї–µ–Ї—Б—Г –У–Є–Ј—Л. –Ъ–ї—О—З–Њ–Љ —П–≤–ї—П—О—В—Б—П –Љ–µ—Б—В–Њ–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –Є —А–∞–Ј–Љ–µ—А—Л –Т–µ–ї–Є–Ї–Њ–є –њ–Є—А–∞–Љ–Є–і—Л, –Ї–Њ—В–Њ—А—Л–µ вАУ –Ї–∞–Ї –Љ—Л —Г–ґ–µ –њ–Њ–Ї–∞–Ј–∞–ї–Є вАУ –љ–∞—Е–Њ–і—П—В—Б—П –≤ –≤—Л—А–∞–ґ–µ–љ–љ–Њ–є —Ж–µ–ї—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є –њ—А–Њ–њ–Њ—А—Ж–Є–Є —Б —А–∞–Ј–Љ–µ—А–∞–Љ–Є –Ч–µ–Љ–ї–Є. –Т –Ї–∞—З–µ—Б—В–≤–µ –µ–і–Є–љ–Є—Ж—Л –Є–Ј–Љ–µ—А–µ–љ–Є—П –њ—А–Є —Б–Њ–Њ—А—Г–ґ–µ–љ–Є–Є –Т–µ–ї–Є–Ї–Њ–є –њ–Є—А–∞–Љ–Є–і—Л –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї—Б—П —Ж–∞—А—Б–Ї–Є–є –ї–Њ–Ї–Њ—В—М. –Ъ–∞–ґ–і–∞—П –µ–µ —Б—В–Њ—А–Њ–љ–∞ –Є–Љ–µ–µ—В 440 —Ж–∞—А—Б–Ї–Є—Е –ї–Њ–Ї—В–µ–є –≤ –і–ї–Є–љ—Г. 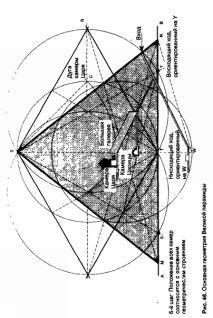  
–Ъ–Њ–љ—Д–Є–≥—Г—А–∞—Ж–Є—П —Б–µ—В–Ї–Є –Є–Ј –Ї–≤–∞–і—А–∞—В–Њ–≤ —Б–Њ —Б—В–Њ—А–Њ–љ–Њ–є –≤ 220 —Ж–∞—А—Б–Ї–Є—Е –ї–Њ–Ї—В–µ–є, —А–∞–≤–љ–Њ–є –њ–Њ–ї–Њ–≤–Є–љ–µ –і–ї–Є–љ—Л —Б—В–Њ—А–Њ–љ—Л –њ–Є—А–∞–Љ–Є–і—Л, –њ—А–Є –љ–∞–ї–Њ–ґ–µ–љ–Є–Є –љ–∞ –њ–ї–∞—В–Њ –У–Є–Ј–∞ –љ–µ–Љ–µ–і–ї–µ–љ–љ–Њ —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞–µ—В –њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –њ–Є—А–∞–Љ–Є–і –•–∞—Д—А—Л –Є –Ь–µ–љ–Ї–∞—Г—А–∞, –∞ —В–∞–Ї–ґ–µ –°—Д–Є–љ–Ї—Б–∞ (—А–Є—Б. 48). –≠—В–∞ –њ—А–Њ—Б—В–∞—П –Ї–Њ–Љ–њ–Њ–Ј–Є—Ж–Є—П —Б–Њ—Е—А–∞–љ—П–µ—В —П—А–Ї–Є–µ —З–Є—Б–ї–Њ–≤—Л–µ –Њ—В–љ–Њ—И–µ–љ–Є—П, –љ–∞–є–і–µ–љ–љ—Л–µ –≤ –њ—А–Њ–њ–Њ—А—Ж–Є—П—Е –Ї–∞–ґ–і–Њ–є –њ–Є—А–∞–Љ–Є–і—Л. –Ю–љ–∞ —Б—А–∞–Ј—Г –ґ–µ –Њ–±—К—П—Б–љ—П–µ—В, –њ–Њ—З–µ–Љ—Г –њ–Є—А–∞–Љ–Є–і–∞ –•–∞—Д—А—Л –љ–∞—Е–Њ–і–Є—В—Б—П –≤–љ–µ –ї–Є–љ–Є–Є –≤ —Б–≤–Њ–µ–Љ –і–Є–∞–≥–Њ–љ–∞–ї—М–љ–Њ–Љ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–Є —Б –Т–µ–ї–Є–Ї–Њ–є –њ–Є—А–∞–Љ–Є–і–Њ–є, –Є —Н—В–Њ –Њ—Б–Њ–±–Њ –њ–Њ–і—З–µ—А–Ї–Є–≤–∞–ї–Є –С—М—О–≤—Н–ї –Є –Ф–ґ–Є–ї–±–µ—А—В –≤ ¬Ђ–Ґ–∞–є–љ–µ –Ю—А–Є–Њ–љ–∞¬ї –Ї–∞–Ї —Б–≤–Є–і–µ—В–µ–ї—М—Б—В–≤–Њ —Б–≤—П–Ј–Є –њ–Є—А–∞–Љ–Є–і —Б –Я–Њ—П—Б–Њ–Љ –Ю—А–Є–Њ–љ–∞. –°–µ–є—З–∞—Б –Љ–Њ–ґ–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ —О–ґ–љ—Л–є –Є –≤–Њ—Б—В–Њ—З–љ—Л–є –Ї—А–∞—П –њ–Є—А–∞–Љ–Є–і—Л –•–∞—Д—А—Л —З–µ—В–Ї–Њ –≤–њ–Є—Б—Л–≤–∞—О—В—Б—П –≤ —Б–µ—В–Ї—Г –°–Љ–µ—Й–µ–љ–Є–µ –і–Є–∞–≥–Њ–љ–∞–ї–Є –≤–Њ–Ј–љ–Є–Ї–∞–µ—В —В–Њ–ї—М–Ї–Њ –њ–Њ—В–Њ–Љ—Г, —З—В–Њ –Њ–љ–∞ –±—Л–ї–∞ –њ–Њ—Б—В —А–Њ–µ–љ–∞ —Б –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ –Љ–µ–љ—М—И–Є–Љ –њ–ї–∞–љ–Њ–Љ –Њ—Б–љ–Њ–≤–∞–љ–Є—П, —З–µ–Љ –Т–µ–ї–Є–Ї–∞—П –њ–Є—А–∞–Љ–Є–і–∞. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 |
|||||||