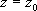Вычегда

Р’С‹'чегда,река РІ РљРѕРјРё РђРЎРЎР  Рё Архангельской области РСФСР, самый большой приток Северной Двины (правый). Длина 1130 РєРј, площадь бассейна 121 тыс. РєРј ². Берет начало РЅР° южной окраине Тиманского кряжа. Р’ верховьях долина узкая, врезана РЅР° 20-40 Рј, имеются РїРѕСЂРѕРіРё. Ниже долина РІ отдельных местах образует озеровидные заболоченные расширения. Русло реки РїРѕРІСЃСЋРґСѓ сопровождается широкой заболоченной РїРѕР№РјРѕР№ СЃ многочисленными старицами Рё озёрами, изобилует песчаными перекатами, участками подмываемых берегов. Питание смешанное, СЃ преобладанием снегового. Средний РіРѕРґРѕРІРѕР№ расход РІРѕРґС‹ Сѓ Сыктывкара 599 Рј ³ /сек, близ устья - 1100 Рј ³ /сек. Замерзает РІ начале РЅРѕСЏР±СЂСЏ, вскрывается РІ конце апреля. Важнейшие притоки: Воль, Вишера, Вымь - справа; Нем, Северная Кельтма, Локчим, Сысола Виледь - слева. Сплавная. Весной СЃСѓРґРѕС…РѕРґРЅР° РґРѕ Вольдино (959 РєРј) РІ летне-осенний период - РґРѕ Усть-Кулома (693 РєРј). Главные пристани: Сольвычегодск, Яренск, Межог, РђР№РєРёРЅРѕ, Сыктывкар, Усть-Кулом.

Вычегодский

Вычего'дский,поселок городского типа в Архангельской области РСФСР. Железнодорожная станция (Сольвычегодск). 10,9 тыс. жителей (1970). Возник в 1942 в связи со строительством железной дороги Котлас - Воркута. Предприятия железнодорожного транспорта.

Вычет

Р’С‹'чет,1) РІ теории чисел. Число аназывается вычетом числа bРїРѕ модулю m, если разность Р°- bделится РЅР° m( a, b, m> 0 - целые числа). Например, число 24 есть Р’. числа 3 РїРѕ модулю 7, так как 24-3 делится РЅР° 7. Совокупность mцелых чисел, каждое РёР· которых является Р’. РѕРґРЅРѕРіРѕ Рё только РѕРґРЅРѕРіРѕ РёР· чисел 0, 1,..., m- 1, называется полной системой Р’. РїРѕ модулю m. Например, числа 1, 6, 11, 16, 21, 26 образуют полную систему Р’. РїРѕ модулю 6. Число аназывается вычетом степени n( n³ 2 - целое) РїРѕ модулю m, если существует целое число С…, такое, что разность x ⁿ - aделится РЅР° m. Р’ противном случае аназывается невычетом степени n. Например, 2 Рё 3, соответственно, вычет Рё невычет второй степени (квадратичные) РїРѕ модулю 7.

  Лит.:Виноградов �. М., Основы теории чисел, 7 изд. М., 1965.

  А. А. Карацуба.

В  2) Р’ теории аналитических функций вычетом однозначной аналитической функции f( z) относительно её изолированной РѕСЃРѕР±РѕР№ точки z ₀называется коэффициент РїСЂРё ( z- z ₀) ^-1РІ разложении этой функции РІ СЂСЏРґ РїРѕ степеням разности ( z- z ₀) ( ) РІ окрестности точки z ₀. Обозначение: выч f( z) [или res f( z)].

В В В В В В В 

Если g - окружность достаточно малого радиуса СЃ центром РІ точке z ₀(такая, что внутри неё функция f( z) РЅРµ имеет особых точек, отличных РѕС‚ z ₀), то

В 

В  Важное значение вычетов вытекает РёР· следующей теоремы. Пусть f( z) - однозначная аналитическая функция РІ области D, Р·Р° исключением изолированных особых точек, Р“- простая замкнутая спрямляемая кривая, принадлежащая области Dвместе СЃРѕ своей внутренностью Рё РЅРµ проходящая через особые точки функции f( z); если z ₁,..., z _n- РІСЃРµ особые точки f( z), лежащие внутри Р“, то

В 

  Поскольку вычеты вычисляются сравнительно просто, эта теорема является эффективным средством для нахождения интегралов.

  Лит. см. при статье .

  А. А. Гончар.

Вычислимая функция

Вычисли'мая фу'нкция,РѕРґРЅРѕ РёР· основных понятий теории алгоритмов. Функция fназывается вычислимой, если существует , перерабатывающий РІСЃСЏРєРёР№ объект С…, для которого определена функция f,РІ объект f( x) Рё РЅРµ применимый РЅРё Рє какому x, для которого fРЅРµ определена. Примеры: С…- натуральное число, f( x) = С… ²; x- пара рациональных чисел x ₁Рё x ₂, f( x) = x ₁: x ₂(эта функция определена лишь для тех x, Сѓ которых x ₂¹0); X- пара X ₁Рё X ₂СЃ целочисленными элементами, f( X) = X ₁ X ₂(эта функция определена лишь для тех X, Сѓ которых число стоблцов РІ X ₁совпадает СЃ числом строк РІ X ₂). Аргументами Рё значениями Р’. С„. РјРѕРіСѓС‚ быть лишь так называемые конструктивные объекты (СЃРј. РІ математике) (РёР±Рѕ лишь СЃ такими объектами РјРѕРіСѓС‚ оперировать алгоритмы); таким образом, функция fтакая, что f( x) С” С…РЅРµ является вычислимой, если её рассматривать РЅР° всей действительной РїСЂСЏРјРѕР№, РЅРѕ является вычислимой, если её рассматривать как функцию натурального или рационального аргумента. Р’. С„., областью определения которой служит натуральный СЂСЏРґ, называется вычислимой последовательностью.

  В. А. Успенский.

Вычислительная математика

Вычисли'тельная матема'тика,раздел математики, включающий круг вопросов, связанных с использованием электронных вычислительных машин (ЭВМ). Содержание термина «В. м.» нельзя считать установившимся, так как эта область интенсивно развивается в связи с быстро растущими применениями ЭВМ в новых направлениях. Часто термин «В. м.» понимается как теория численных методов и алгоритмов решения типовых математических задач. Это толкование термина «В. м.» получило распространение на первоначальном этапе, когда использование ЭВМ предъявило новые требования к численным методам; основной задачей на этом этапе была разработка новых методов, «удобных» для ЭВМ. Ниже В. м. понимается в первом - широком смысле этого термина.

  В В. м. можно выделить следующие три больших раздела. Первый связан с применением ЭВМ в различных областях научной и практической деятельности и может быть охарактеризован как анализ математических моделей. Второй - с разработкой методов и алгоритмов решения типовых математических задач, возникающих при исследованиях математических моделей. Третий раздел связан с вопросом об упрощении взаимоотношений человека с ЭВМ, включая теорию и практику программирования задач для ЭВМ, в том числе автоматизацию программирования задач для ЭВМ.

  Анализ математических моделей включает в себя изучение постановки задачи, выбор модели, анализ и обработку входной информации, численное решение математических задач, возникающих в связи с исследованием модели, анализ результатов вычислений, и, наконец, вопросы, связанные с реализацией полученных результатов. Задача выбора модели должна решаться с учётом следующего требования. Степень достоверности, с которой результаты анализа модели позволяют исследовать конкретное явление (или класс явлений), должна соответствовать точности исходной информации. При этом с появлением возможности получать более точную информацию обычно возникает необходимость совершенствования построенной модели, а в ряде случаев даже коренной её замены. Для этих задач приобретает существенное значение обработка исходной информации, что в большинстве случаев требует привлечения методов математической статистики. Математические модели сыграли важную роль в развитии естествознания; в настоящее время использование математических моделей является существенным фактором в широком диапазоне человеческой деятельности (в том числе в вопросах управления, планирования, прогнозирования и т.д.).

  �зучение реальных явлений на основе анализа построенных моделей, как правило, требует развития и привлечения ЭВМ. Таким образом, в В. м. важное место занимают численные методы решения поставленных математических задач и в первую очередь типовых математических задач (В. м. в узком смысле слова).

  В качестве примера типовых математических задач, часто встречающихся в приложениях, можно назвать задачи алгебры: здесь большое значение имеют численные методы решения систем линейных алгебраических уравнений (в частности, больших систем), обращение матриц, нахождение собственных значений матриц (как нескольких первых значений - ограниченная проблема собственных значений, так и нахождение всех собственных значений - полная проблема собственных значений). Другие примеры - численные методы дифференцирования и интегрирования функций одного или нескольких переменных; численные методы решения обыкновенных дифференциальных уравнений (сюда включают, в частности, изучение и сравнительный анализ численных методов различных типов, например, Адамса, Рунге - Кутта). Значительное число исследований посвящено численным методам решения уравнений с частными производными. Здесь большое направление составляют «экономичные методы», т. е. методы, позволяющие получать результаты при относительно малом (экономном) числе операций.

  Быстро развивающимся направлением В. м. являются численные методы оптимизации. Задача оптимизации состоит в изучении экстремальных (наибольших или наименьших) значений функционалов на множествах, как правило, весьма сложной структуры. В первую очередь следует упомянуть задачи (в том числе линейного и динамического), к которым сводятся многие задачи экономики. К задачам оптимизации примыкают минимаксные задачи (и соответствующие численные методы), возникающие при решении задач исследования операций (см. ) и теории игр (см. ). Особенно сложные задачи типа minmaxminmax возникают при решении многошаговых (динамически развивающихся) игр. Здесь даже математический эксперимент (проигрывание вариантов поведения играющих) невозможен без использования мощных ЭВМ.

  Применение ЭВМ к решению сложных задач, в особенности задач больших размеров, вызвало к жизни одно из главных направлений в теории численных методов - исследования устойчивости методов и алгоритмов к различного рода ошибкам (в том числе к ошибкам округления).

  Обратные задачи, например, задача определения элемента хиз уравнения Ах= bпри известной информации об операторе Аи элементе b, часто являются неустойчивыми (некорректно поставленными) задачами (малым погрешностям во входных данных могут соответствовать большие погрешности в х). Более того, обратные задачи часто имеют решение не для всех b, поэтому, задавая приближённое значение b, следует учитывать, что формально решение этой задачи может не существовать.

  Неустойчивые задачи потребовали специального определения понятия приближённых решений и развития соответствующих методов для их нахождения. К неустойчивым задачам относится широкий класс задач, связанных с проблемами автоматизации обработки результатов экспериментов.

  В большинстве разделов В. м. важное место занимают вопросы оптимизации методов решения задач. Особенно это существенно для задач большего объёма (например, с большим числом переменных).

  Применение ЭВМ непрерывно расширяет круг пользователей и поэтому возникает тенденция такой степени автоматизации, при которой становится менее существенным знакомство пользователей с численными методами. Это предъявляет новые требования к алгоритмам, их классификации и к стандартным программам решения типовых задач.

  В настоящее время выделился ряд направлений прикладной науки, где современные темпы научно-технического прогресса были бы немыслимы без развития численных методов и применения ЭВМ.

  Основной задачей теории можно считать облегчение отношений человека с машиной, хотя этот взгляд и конкретное направление исследований претерпевают радикальные изменения с развитием вычислительной техники. Смена ряда поколений вычислительных машин обусловила смену трёх этапов в развитии программирования.

  От составления программ на внутреннем языке машины программирование быстро перешло к составлению стандартных программ решения типовых задач и комплексов таких программ. При их употреблении для широкого класса задач отпадает необходимость в программировании метода решения; достаточно лишь ограничиться заданием исходной информации. Однако задание такой информации, а также написание нестандартных блоков всё равно требуют существенного объёма программирования на языке машины.

  Появление машин следующего поколения с бо'льшим быстродействием сопровождалось ростом числа задач, предъявляемых к решению; в результате этого возникло узкое место системы человек - машина: скорость программирования. Это вызвало к жизни новый этап программирования- создание алгоритмических языков с трансляторами для перевода с алгоритмического языка на внутренний язык машины. Вследствие большей близости алгоритмических языков к общечеловеческому их внедрение упростило программирование и существенно расширило круг пользователей.

  Наряду с созданием универсальных алгоритмических языков (алгол, фортан) был разработан ряд проблемно-ориентированных языков для определённого круга пользователей, например связанных с задачами обработки экономической информации, Создание специализированных языков вызвано следующим: универсальные языки и трансляторы, предназначенные для решения широкого класса задач, иногда слабо учитывают специфику отдельных важных классов задач, что снижает эффективность использования всех возможностей машины.

  При дальнейшем повышении скорости ЭВМ узким местом системы человек - машина стали устройства для ввода и вывода информации; их медленная работа сводила на нет высокопроизводительную работу центрального устройства. Необходимость преодоления этого противоречия явилась одной из причин создания систем одновременного решения на машине нескольких задач. Другой причиной было требование одновременной работы на машине большого коллектива пользователей (в частности, последнее особенно существенно при применении ЭВМ в автоматизированных системах управления). Всё это вместе с рядом других причин обусловило появление нового этапа программирования - системного программирования. Основной задачей системного программирования является создание операционных систем, управляющих работой машины, программным путём расширяющих возможности машины и предоставляющих пользователю дополнительное обслуживание, не предусмотренное аппаратурой: возможность ввода и вывода одновременно с решением задач, автоматизация редактирования выдачи, вывод графиков, работа с экраном, диалог с машиной, возможность одновременного решения на машине многих задач (система разделения времени).

  Развитие применения ЭВМ характерно также организацией работы комплексов, включающих большое число машин, в том числе машин различных типов, вводные устройства, каналы связи между машинами и пользователем, а зачастую и физические установки. Такие высокопроизводительные системы создаются, например, для решения задач экономики и обработки физических экспериментов, требующих ввода и обработки большого количества информации.