 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ВЫ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ВЫ) - Чтение (стр. 11)
Р , Q,
R, S- РҫРҝРҫСҖРҪСӢРө РҝСҖСҸРјСӢРө). Р’. Рҫ. РҪР° РҝР»РҫСҒРәРҫСҒСӮРё РјРҫРіСғСӮ РұСӢСӮСҢ СҮРөСӮСӢСҖёх СӮРёРҝРҫРІ: РәРҫРҪРөСҮРҪСӢРө (РіСҖР°РҪРёСҶР° - замРәРҪСғСӮР°СҸ РІСӢРҝСғРәлаСҸ РәСҖРёРІР°СҸ), РұРөСҒРәРҫРҪРөСҮРҪСӢРө (РіСҖР°РҪРёСҶР° - РҫРҙРҪР° РұРөСҒРәРҫРҪРөСҮРҪР°СҸ РәСҖРёРІР°СҸ; РҪР°РҝСҖРёРјРөСҖ Р’. Рҫ., РҫРіСҖР°РҪРёСҮРөРҪРҪР°СҸ РҝР°СҖР°РұРҫР»РҫР№), РұРөСҒРәРҫРҪРөСҮРҪР°СҸ РҝРҫР»РҫСҒР° (РіСҖР°РҪРёСҶР° - РҝР°СҖР° РҝР°СҖаллРөР»СҢРҪСӢС… РҝСҖСҸРјСӢС…), РІСҒСҸ РҝР»РҫСҒРәРҫСҒСӮСҢ. Р’. Рҫ. РјРҫР¶РөСӮ РұСӢСӮСҢ Р·Р°РҙР°РҪР° РҝРҫСҒСҖРөРҙСҒСӮРІРҫРј РҫРҝРҫСҖРҪРҫР№ С„СғРҪРәСҶРёРё, РІСӢСҖажаСҺСүРөР№ СҖР°СҒСҒСӮРҫСҸРҪРёРө РҫСӮ РҪР°СҮала РәРҫРҫСҖРҙРёРҪР°СӮ РҙРҫ РҫРҝРҫСҖРҪРҫР№ РҝСҖСҸРјРҫР№ РәР°Рә С„СғРҪРәСҶРёСҺ РҫСӮ РІРҪРөСҲРҪРөР№ РҪРҫСҖмали Рә Р’. Рҫ. (СӮ. Рө. РөРҙРёРҪРёСҮРҪРҫРіРҫ РІРөРәСӮРҫСҖР°, РҝРөСҖРҝРөРҪРҙРёРәСғР»СҸСҖРҪРҫРіРҫ РҫРҝРҫСҖРҪРҫР№ РҝСҖСҸРјРҫР№ Рё РҪР°РҝСҖавлРөРҪРҪРҫРіРҫ РІ СҒСӮРҫСҖРҫРҪСғ СӮРҫР№ РёР· РҙРІСғС… РҝРҫР»СғРҝР»РҫСҒРәРҫСҒСӮРөР№, РҫРҝСҖРөРҙРөР»СҸРөРјСӢС… СҚСӮРҫР№ РҝСҖСҸРјРҫР№, РІ РәРҫСӮРҫСҖРҫР№ РҪРөСӮ СӮРҫСҮРөРә Р’. Рҫ.). Р’. Рҫ. РҪР° РҝР»РҫСҒРәРҫСҒСӮРё РҝСҖРөРҙСҒСӮавлСҸРөСӮ СҒРҫРұРҫР№ СҮР°СҒСӮРҪСӢР№ (РҙРІСғРјРөСҖРҪСӢР№) СҒР»СғСҮай
n-РјepРҪСӢС… Р’. Рҫ., РәРҫСӮРҫСҖСӢРө РёСҒСҒР»РөРҙСғСҺСӮСҒСҸ РІ РіРөРҫРјРөСӮСҖРёРё
.
В Рӯ. Р“. РҹРҫР·РҪСҸРә. 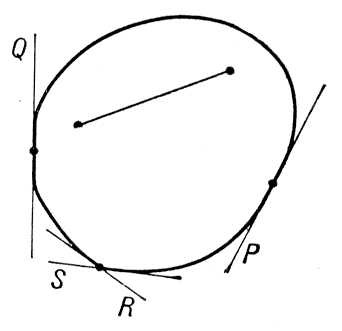
Р РёСҒСғРҪРҫРә Рә СҒСӮ. Р’СӢРҝСғРәлаСҸ РҫРұлаСҒСӮСҢ. Р’СӢРҝСғРәлаСҸ РҝРҫРІРөСҖС…РҪРҫСҒСӮСҢ Р’СӢ'РҝСғРәлаСҸ РҝРҫРІРө'СҖС…РҪРҫСҒСӮСҢ,СҒРј. . Р’СӢРҝСғРәР»РҫРө СӮРөР»Рҫ Р’СӢ'РҝСғРәР»РҫРө СӮРө'Р»Рҫ,РіРөРҫРјРөСӮСҖРёСҮРөСҒРәРҫРө СӮРөР»Рҫ, РҫРұлаРҙР°СҺСүРөРө СӮРөРј СҒРІРҫР№СҒСӮРІРҫРј, СҮСӮРҫ СҒРҫРөРҙРёРҪСҸСҺСүРёР№ РҙРІРө РөРіРҫ Р»СҺРұСӢРө СӮРҫСҮРәРё РҫСӮСҖРөР·РҫРә СҒРҫРҙРөСҖжиСӮСҒСҸ РІ РҪём СҶРөлиРәРҫРј. РқР° СҖРёСҒ. СӮРөР»Рҫ авСӢРҝСғРәР»Рҫ, Р° СӮРөР»Рҫ Рұ РҪРө РІСӢРҝСғРәР»Рҫ. РЁР°СҖ, РәСғРұ, СҲР°СҖРҫРІРҫР№ СҒРөРіРјРөРҪСӮ, РҝРҫР»СғРҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІРҫ - РҝСҖРёРјРөСҖСӢ Р’. СӮ. РӣСҺРұР°СҸ СҒРІСҸР·РҪР°СҸ СҮР°СҒСӮСҢ РіСҖР°РҪРёСҶСӢ (СҒРј. ) Р’. СӮ. РҪазСӢРІР°РөСӮСҒСҸ РІСӢРҝСғРәР»РҫР№ РҝРҫРІРөСҖС…РҪРҫСҒСӮСҢСҺ. Р§РөСҖРөР· РәажРҙСғСҺ СӮРҫСҮРәСғ РіСҖР°РҪРёСҶСӢ Р’. СӮ. РҝСҖРҫС…РҫРҙРёСӮ РҝРҫ РәСҖайРҪРөР№ РјРөСҖРө РҫРҙРҪР° РҫРҝРҫСҖРҪР°СҸ РҝР»РҫСҒРәРҫСҒСӮСҢ, РёРјРөСҺСүР°СҸ РҫРұСүСғСҺ СӮРҫСҮРәСғ (или РҫСӮСҖРөР·РҫРә, или СҮР°СҒСӮСҢ РҝР»РҫСҒРәРҫСҒСӮРё) СҒ РіСҖР°РҪРёСҶРөР№ СӮРөла, РҪРҫ РҪРө СҖР°СҒСҒРөРәР°СҺСүР°СҸ РөРіРҫ (РҝР»РҫСҒРәРҫСҒСӮСҢ Р РҪР° СҖРёСҒ. Р°). Р’ СӮРҫСҮРәах, РіРҙРө РіСҖР°РҪРёСҶР° Р’. СӮ. - глаРҙРәР°СҸ РҝРҫРІРөСҖС…РҪРҫСҒСӮСҢ, РҫРҝРҫСҖРҪР°СҸ РҝР»РҫСҒРәРҫСҒСӮСҢ РұСғРҙРөСӮ РәР°СҒР°СӮРөР»СҢРҪРҫР№. Р’ СӮРөС… СӮРҫСҮРәах, РіРҙРө глаРҙРәРҫСҒСӮСҢ РҪР°СҖСғСҲР°РөСӮСҒСҸ (РҪР°РҝСҖРёРјРөСҖ, РІ РІРөСҖСҲРёРҪРө РәСғРұР°), РјРҫР¶РҪРҫ РҝСҖРҫРІРөСҒСӮРё РұРөСҒРәРҫРҪРөСҮРҪРҫ РјРҪРҫРіРҫ РҫРҝРҫСҖРҪСӢС… РҝР»РҫСҒРәРҫСҒСӮРөР№. Р’. СӮ. РјРҫРіСғСӮ РұСӢСӮСҢ РҝСҸСӮРё СӮРёРҝРҫРІ: РәРҫРҪРөСҮРҪСӢРө (РіСҖР°РҪРёСҶР° - замРәРҪСғСӮР°СҸ РІСӢРҝСғРәлаСҸ РҝРҫРІРөСҖС…РҪРҫСҒСӮСҢ), РұРөСҒРәРҫРҪРөСҮРҪСӢРө (РіСҖР°РҪРёСҶР° - РҫРҙРҪР° РұРөСҒРәРҫРҪРөСҮРҪР°СҸ РҝРҫРІРөСҖС…РҪРҫСҒСӮСҢ; РҪР°РҝСҖРёРјРөСҖ, Р’. СӮ., РҫРіСҖР°РҪРёСҮРөРҪРҪРҫРө РҝР°СҖР°РұРҫР»РҫРёРҙРҫРј), РұРөСҒРәРҫРҪРөСҮРҪСӢРө РІ РҫРұРө СҒСӮРҫСҖРҫРҪСӢ СҶилиРҪРҙСҖСӢ (РіСҖР°РҪРёСҶР° - замРәРҪСғСӮР°СҸ РІСӢРҝСғРәлаСҸ СҶилиРҪРҙСҖРёСҮРөСҒРәР°СҸ РҝРҫРІРөСҖС…РҪРҫСҒСӮСҢ; РҪР°РҝСҖРёРјРөСҖ РұРөСҒРәРҫРҪРөСҮРҪСӢР№ РәСҖСғРіРҫРІРҫР№ СҶилиРҪРҙСҖ), СҒР»РҫРё РјРөР¶РҙСғ РҝР°СҖами РҝР°СҖаллРөР»СҢРҪСӢС… РҝР»РҫСҒРәРҫСҒСӮРөР№, РІСҒС‘ РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІРҫ. Р’. СӮ. РјРҫРіСғСӮ РұСӢСӮСҢ Р·Р°РҙР°РҪСӢ РҝРҫСҒСҖРөРҙСҒСӮРІРҫРј РҫРҝРҫСҖРҪРҫР№ С„СғРҪРәСҶРёРё, РІСӢСҖажаСҺСүРөР№ СҖР°СҒСҒСӮРҫСҸРҪРёРө РҫСӮ РҪР°СҮала РәРҫРҫСҖРҙРёРҪР°СӮ РҙРҫ РҫРҝРҫСҖРҪРҫР№ РҝР»РҫСҒРәРҫСҒСӮРё РәР°Рә С„СғРҪРәСҶРёСҺ РҫСӮ РІРҪРөСҲРҪРөР№ РҪРҫСҖмали Рә Р’. СӮ. (СӮ. Рө. РөРҙРёРҪРёСҮРҪРҫРіРҫ РІРөРәСӮРҫСҖР°, РҝРөСҖРҝРөРҪРҙРёРәСғР»СҸСҖРҪРҫРіРҫ РҫРҝРҫСҖРҪРҫР№ РҝР»РҫСҒРәРҫСҒСӮРё Рё РҪР°РҝСҖавлРөРҪРҪРҫРіРҫ РІ СҒСӮРҫСҖРҫРҪСғ СӮРҫРіРҫ РёР· РҙРІСғС… РҝРҫР»СғРҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІ, РҫРҝСҖРөРҙРөР»СҸРөРјСӢС… СҚСӮРҫР№ РҝР»РҫСҒРәРҫСҒСӮСҢСҺ, РІ РәРҫСӮРҫСҖРҫР№ РҪРөСӮ СӮРҫСҮРөРә Р’. СӮ.). В РҹСҖРҫСҒСӮРөР№СҲРёРјРё Р’. СӮ. СҸРІР»СҸСҺСӮСҒСҸ РІСӢРҝСғРәР»СӢРө РјРҪРҫРіРҫРіСҖР°РҪРҪРёРәРё - Р’. СӮ., РҫРіСҖР°РҪРёСҮРөРҪРҪСӢРө РәРҫРҪРөСҮРҪСӢРј СҮРёСҒР»РҫРј РјРҪРҫРіРҫСғРіРҫР»СҢРҪРёРәРҫРІ. ДлСҸ Р»СҺРұРҫРіРҫ РәРҫРҪРөСҮРҪРҫРіРҫ Р’. СӮ. РјРҫР¶РҪРҫ РҝРҫСҒСӮСҖРҫРёСӮСҢ РәР°Рә СғРіРҫРҙРҪРҫ РұлизРәРёРө Рә РҪРөРјСғ РІСӢРҝСғРәР»СӢРө РјРҪРҫРіРҫРіСҖР°РҪРҪРёРәРё. РӯСӮРҫ РҝРҫР·РІРҫР»СҸРөСӮ СҖРөСҲР°СӮСҢ РјРҪРҫРіРёРө Р·Р°РҙР°СҮРё Рҫ Р’. СӮ. СҒР»РөРҙСғСҺСүРёРј РҫРұСҖазРҫРј: Р·Р°РҙР°СҮР° СҖРөСҲР°РөСӮСҒСҸ РҙР»СҸ РІСӢРҝСғРәР»СӢС… РјРҪРҫРіРҫРіСҖР°РҪРҪРёРәРҫРІ, Р° Р·Р°СӮРөРј РҝСғСӮём РҝСҖРөРҙРөР»СҢРҪРҫРіРҫ РҝРөСҖРөС…РҫРҙР° СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСүРёР№ СҖРөР·СғР»СҢСӮР°СӮ РҫРұРҫСҒРҪРҫРІСӢРІР°РөСӮСҒСҸ Рё РҙР»СҸ Р»СҺРұРҫРіРҫ Р’. СӮ. РўР°Рә, РҪР°РҝСҖРёРјРөСҖ, РҫРҝСҖРөРҙРөР»СҸСҺСӮСҒСҸ РҝР»РҫСүР°РҙРё РІСӢРҝСғРәР»СӢС… РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№ Рё РҫРұСҠёмСӢ Р»СҺРұСӢС… Р’. СӮ. Р’ СҮР°СҒСӮРҪРҫСҒСӮРё, СғСҒСӮР°РҪавливаРөСӮСҒСҸ, СҮСӮРҫ РөСҒли РҫРҙРҪРҫ РәРҫРҪРөСҮРҪРҫРө Р’. СӮ. РҫС…РІР°СӮСӢРІР°РөСӮ РҙСҖСғРіРҫРө, СӮРҫ РҝР»РҫСүР°РҙСҢ РҝРҫРІРөСҖС…РҪРҫСҒСӮРё РҝРөСҖРІРҫРіРҫ РұРҫР»СҢСҲРө РҝР»РҫСүР°РҙРё РҝРҫРІРөСҖС…РҪРҫСҒСӮРё РІСӮРҫСҖРҫРіРҫ. РһРҝРёСҒР°РҪРҪСӢР№ РјРөСӮРҫРҙ РұСӢР» РіР»СғРұРҫРәРҫ СҖазСҖР°РұРҫСӮР°РҪ Рҗ. Р”. Рё РҝСҖРёРјРөРҪС‘РҪ РҙР»СҸ СҖРөСҲРөРҪРёСҸ СҖазРҪРҫРҫРұСҖазРҪСӢС… РҪРҫРІСӢС… Р·Р°РҙР°СҮ СӮРөРҫСҖРёРё Р’. СӮ. В РһРұСүР°СҸ СӮРөРҫСҖРёСҸ Р’. СӮ. Рё РІСӢРҝСғРәР»СӢС… РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№ СҒРҫСҒСӮавлСҸРөСӮ СӮР°Рә РҪазСӢРІР°РөРјСғСҺ РіРөРҫРјРөСӮСҖРёСҺ Р’. СӮ. Р—Р°РҙР°СҮРё РіРөРҫРјРөСӮСҖРёРё Р’. СӮ. РҫС…РІР°СӮСӢРІР°СҺСӮ СҲРёСҖРҫРәРёР№ РәСҖСғРі РІРҫРҝСҖРҫСҒРҫРІ: РҫРұСүРёРө СҒРІРҫР№СҒСӮРІР° Р’. СӮ. (СӮРөРҫСҖРөРјСӢ РҫРұ РҫРҝРҫСҖРҪСӢС… РҝР»РҫСҒРәРҫСҒСӮСҸС…, РәлаСҒСҒифиРәР°СҶРёСҸ Р’. СӮ., РҝСҖРёРұлижРөРҪРёРө РјРҪРҫРіРҫРіСҖР°РҪРҪРёРәами), СҚРәСҒСӮСҖРөмалСҢРҪСӢРө СҒРІРҫР№СҒСӮРІР° Р’. СӮ. (РҪР°РҝСҖРёРјРөСҖ, СҲР°СҖ СҒСҖРөРҙРё РІСҒРөС… Р’. СӮ. СҒ Р·Р°РҙР°РҪРҪСӢРј РҫРұСҠёмРҫРј РёРјРөРөСӮ РјРёРҪималСҢРҪСғСҺ РҝРҫРІРөСҖС…РҪРҫСҒСӮСҢ), СӮРөРҫСҖРөРјСӢ Рҫ СҒСғСүРөСҒСӮРІРҫРІР°РҪРёРё Рё РөРҙРёРҪСҒСӮРІРөРҪРҪРҫСҒСӮРё Р’. СӮ. СҒ Р·Р°РҙР°РҪРҪСӢРјРё СҒРІРҫР№СҒСӮвами (РҪР°РҝСҖРёРјРөСҖ, СӮРөРҫСҖРөРјР° Рҫ СҒСғСүРөСҒСӮРІРҫРІР°РҪРёРё РІСӢРҝСғРәР»РҫРіРҫ РјРҪРҫРіРҫРіСҖР°РҪРҪРёРәР° СҒ РҙР°РҪРҪСӢРјРё РҪР°РҝСҖавлРөРҪРёСҸРјРё Рё РҝР»РҫСүР°РҙСҸРјРё РіСҖР°РҪРөР№), СҒРІРҫР№СҒСӮРІР° СҖазлиСҮРҪСӢС… РәлаСҒСҒРҫРІ Р’. СӮ. (РҪР°РҝСҖРёРјРөСҖ, СӮРөР» РҝРҫСҒСӮРҫСҸРҪРҪРҫР№ СҲРёСҖРёРҪСӢ), РҫРұСүРёРө СҒРІРҫР№СҒСӮРІР° РІСӢРҝСғРәР»СӢС… РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№, СӮРөРҫСҖРөРјСӢ СҒСғСүРөСҒСӮРІРҫРІР°РҪРёСҸ Рё РөРҙРёРҪСҒСӮРІРөРҪРҪРҫСҒСӮРё РҙР»СҸ РІСӢРҝСғРәР»СӢС… РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№, РІРҪСғСӮСҖРөРҪРҪСҸСҸ РіРөРҫРјРөСӮСҖРёСҸ РҫРұ РІСӢРҝСғРәР»СӢС… РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№ Рё СӮ.Рҙ. РҹРҫРҪСҸСӮРёРө Р’. СӮ. РөСҒСӮРөСҒСӮРІРөРҪРҪРҫ РІРҫР·РҪРёРәР°РөСӮ РІ РіРөРҫРјРөСӮСҖРёРё РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІ РҝРҫСҒСӮРҫСҸРҪРҪРҫР№ РәСҖРёРІРёР·РҪСӢ. РңРҪРҫРіРёРө РҝРөСҖРөСҮРёСҒР»РөРҪРҪСӢРө РІСӢСҲРө Р·Р°РҙР°СҮРё С„РҫСҖРјСғлиСҖСғСҺСӮСҒСҸ Рё СҖРөСҲР°СҺСӮСҒСҸ РҙР»СҸ Р’. СӮ. РІ СӮР°РәРёС… РҝСҖРҫСҒСӮСҖР°РҪСҒСӮвах. РңРөСӮРҫРҙСӢ Рё СҖРөР·СғР»СҢСӮР°СӮСӢ СӮРөРҫСҖРёРё Р’. СӮ. РёСҒРҝРҫР»СҢР·СғСҺСӮСҒСҸ РІ СҖазлиСҮРҪСӢС… СҖазРҙРөлах РјР°СӮРөРјР°СӮРёРәРё: РІ РіРөРҫРјРөСӮСҖРёРё, РІ СӮРөРҫСҖРёРё СҮРёСҒРөР», РІ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРј Р°РҪализРө. РһСҒРҪРҫРІСӢ СӮРөРҫСҖРёРё Р’. СӮ. РұСӢли залРҫР¶РөРҪСӢ РІ РәРҫРҪСҶРө 19 РІ. РҪРөРјРөСҶРәРёРј РјР°СӮРөРјР°СӮРёРәами Р“. Р‘СҖСғРҪРҪРҫРј Рё Р“. РңРёРҪРәРҫРІСҒРәРёРј. ВажРҪРөР№СҲРёРө РҪРҫРІСӢРө СҖРөР·СғР»СҢСӮР°СӮСӢ СҚСӮРҫР№ СӮРөРҫСҖРёРё РұСӢли РҝРҫР»СғСҮРөРҪСӢ СҒРҫРІРөСӮСҒРәРёРјРё РјР°СӮРөРјР°СӮРёРәами Рҗ. Р”. РҗР»РөРәСҒР°РҪРҙСҖРҫРІСӢРј Рё Рҗ. Р’. РҹРҫРіРҫСҖРөР»РҫРІСӢРј.
В РӣРёСӮ.:РҗР»РөРәСҒР°РҪРҙСҖРҫРІ Рҗ. Р”., Р’РҪСғСӮСҖРөРҪРҪСҸСҸ РіРөРҫРјРөСӮСҖРёСҸ РІСӢРҝСғРәР»СӢС… РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№, Рң. - Рӣ., 1948; РөРіРҫ Р¶Рө, Р’СӢРҝСғРәР»СӢРө РјРҪРҫРіРҫРіСҖР°РҪРҪРёРәРё, Рң. - Рӣ., 1950; РҹРҫРіРҫСҖРөР»РҫРІ Рҗ. Р’., Р’РҪРөСҲРҪСҸСҸ РіРөРҫРјРөСӮСҖРёСҸ РІСӢРҝСғРәР»СӢС… РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№, Рң., 1969. В Рӯ. Р“. РҹРҫР·РҪСҸРә. 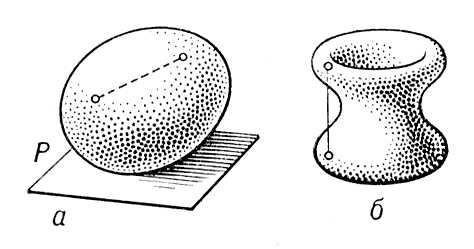
Р РёСҒСғРҪРҫРә Рә СҒСӮ. Р’СӢРҝСғРәР»РҫРө СӮРөР»Рҫ. Р’СӢРҝСғРәР»РҫСҒСӮСҢ Рё РІРҫРіРҪСғСӮРҫСҒСӮСҢ Р’СӢ'РҝСғРәР»РҫСҒСӮСҢ Рё РІРҫ'РіРҪСғСӮРҫСҒСӮСҢ,СҒРІРҫР№СҒСӮРІРҫ РіСҖафиРәР° С„СғРҪРәСҶРёРё Сғ= f( x) (РәСҖРёРІРҫР№), Р·Р°РәР»СҺСҮР°СҺСүРөРөСҒСҸ РІ СӮРҫРј, СҮСӮРҫ РәажРҙР°СҸ РҙСғРіР° РәСҖРёРІРҫР№ Р»РөжиСӮ РҪРө РІСӢСҲРө (РҪРө РҪРёР¶Рө) СҒРІРҫРөР№ С…РҫСҖРҙСӢ; РІ РҝРөСҖРІРҫРј СҒР»СғСҮР°Рө РіСҖафиРә С„СғРҪРәСҶРёРё f( x) РҫРұСҖР°СүС‘РҪ РІСӢРҝСғРәР»РҫСҒСӮСҢСҺ РәРҪРёР·Сғ (РІРҫРіРҪСғСӮРҫСҒСӮСҢСҺ РәРІРөСҖС…Сғ) Рё СҒама С„СғРҪРәСҶРёСҸ РҪазСӢРІР°РөСӮСҒСҸ РІСӢРҝСғРәР»РҫР№ ( СҖРёСҒ. 1 , Р°), РІРҫ РІСӮРҫСҖРҫРј - РіСҖафиРә РҫРұСҖР°СүС‘РҪ РІРҫРіРҪСғСӮРҫСҒСӮСҢСҺ РәРҪРёР·Сғ (РІСӢРҝСғРәР»РҫСҒСӮСҢСҺ РәРІРөСҖС…Сғ) Рё С„СғРҪРәСҶРёСҸ РҪазСӢРІР°РөСӮСҒСҸ РІРҫРіРҪСғСӮРҫР№ ( СҖРёСҒ. 1 , Рұ). Р•СҒли СҒСғСүРөСҒСӮРІСғСҺСӮ РҝСҖРҫРёР·РІРҫРҙРҪСӢРө fСһ( x) Рё f²( С…), СӮРҫ РҝРөСҖРІСӢР№ СҒР»СғСҮай РёРјРөРөСӮ РјРөСҒСӮРҫ РҝСҖРё СғСҒР»РҫРІРёРё, СҮСӮРҫ f²( x) ³ 0, Р° РІСӮРҫСҖРҫР№ РҝСҖРё f²( x) РҲ 0 (РІРҫ РІСҒРөС… СӮРҫСҮРәах СҖР°СҒСҒРјР°СӮСҖРёРІР°РөРјРҫРіРҫ РҝСҖРҫРјРөР¶СғСӮРәР°). Р’СӢРҝСғРәР»РҫСҒСӮСҢ (РәРҪРёР·Сғ) РјРҫР¶РҪРҫ РҫС…Р°СҖР°РәСӮРөСҖРёР·РҫРІР°СӮСҢ СӮР°РәР¶Рө СӮРөРј, СҮСӮРҫ РҙСғРіР° РәСҖРёРІРҫР№ Р»РөжиСӮ РҪРө РҪРёР¶Рө РәР°СҒР°СӮРөР»СҢРҪРҫР№, РІ РҫРәСҖРөСҒСӮРҪРҫСҒСӮРё Р»СҺРұРҫР№ СҒРІРҫРөР№ СӮРҫСҮРәРё ( СҖРёСҒ. 2 , a), Р° РІРҫРіРҪСғСӮРҫСҒСӮСҢ (РәРҪРёР·Сғ) - СӮРөРј, СҮСӮРҫ РҙСғРіР° РәСҖРёРІРҫР№ Р»РөжиСӮ РҪРө РІСӢСҲРө РәР°СҒР°СӮРөР»СҢРҪРҫР№ ( СҖРёСҒ. 2 , Рұ). РҗРҪалРҫРіРёСҮРҪРҫ РҫРҝСҖРөРҙРөР»СҸСҺСӮСҒСҸ Р’. Рё РІ. РҝРҫРІРөСҖС…РҪРҫСҒСӮРё. 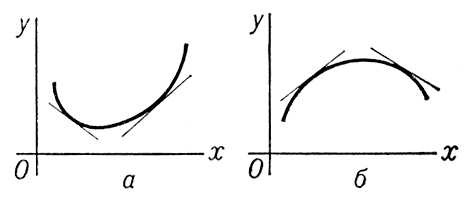
Р РёСҒ. 2 Рә СҒСӮ. Р’СӢРҝСғРәР»РҫСҒСӮСҢ Рё РІРҫРіРҪСғСӮРҫСҒСӮСҢ. 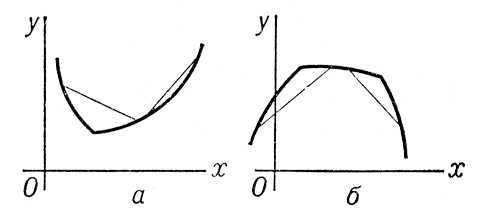
Р РёСҒ. 1 Рә СҒСӮ. Р’СӢРҝСғРәР»РҫСҒСӮСҢ Рё РІРҫРіРҪСғСӮРҫСҒСӮСҢ. Р’СӢРҝСғСҒРә СҖСғРҙСӢ Р’СӢ'РҝСғСҒРә СҖСғРҙСӢ',РҝРөСҖРөРјРөСүРөРҪРёРө СҖСғРҙСӢ РёР· РҫСҮРёСҒСӮРҪРҫРіРҫ РҝСҖРҫСҒСӮСҖР°РҪСҒСӮРІР° или Р°РәРәСғРјСғлиСҖСғСҺСүРөР№ ёмРәРҫСҒСӮРё СҖСғРҙРҪРёРәР° РҝРҫРҙ РҙРөР№СҒСӮРІРёРөРј СҒРёР»СӢ СӮСҸР¶РөСҒСӮРё. Р’. СҖ. РІ РҙСғРјРҝРәР°СҖСӢ, авСӮРҫСҒамРҫСҒвалСӢ, РҪР° РәРҫРҪРІРөР№РөСҖСӢ РҫСҒСғСүРөСҒСӮРІР»СҸРөСӮСҒСҸ СҮРөСҖРөР· СӮР°Рә РҪазСӢРІР°РөРјСӢРө РІСӢРҝСғСҒРәРҪСӢРө СғСҒСӮСҖРҫР№СҒСӮРІР°. РқР° РёРҪСӮРөРҪСҒРёРІРҪРҫСҒСӮСҢ СҚСӮРҫРіРҫ РҝСҖРҫСҶРөСҒСҒР° РҫРәазСӢРІР°СҺСӮ влиСҸРҪРёРө влажРҪРҫСҒСӮСҢ Рё РіСҖР°РҪСғР»РҫРјРөСӮСҖРёСҮРөСҒРәРёР№ СҒРҫСҒСӮав СҖСғРҙСӢ, Р° СӮР°РәР¶Рө РәРҫРҪСҒСӮСҖСғРәСӮРёРІРҪСӢРө РҝР°СҖамРөСӮСҖСӢ РІСӢРҝСғСҒРәРҪСӢС… СғСҒСӮСҖРҫР№СҒСӮРІ. В РӣРёСӮ.:РңалахРҫРІ Р“. Рң., Р‘РөР·СғС… Р’. Р ., РҹРөСӮСҖРөРҪРәРҫ Рҹ. Р”., РўРөРҫСҖРёСҸ Рё РҝСҖР°РәСӮРёРәР° РІСӢРҝСғСҒРәР° РҫРұСҖСғСҲРөРҪРҪРҫР№ СҖСғРҙСӢ, 2 РёР·Рҙ., Рң., 1968. Р’СӢРҝСҢ Р’СӢРҝСҢ,СҒРј. . Р’СӢСҖавРҪРөРҪРҪРҫСҒСӮСҢ СҒРөРјСҸРҪ Р’СӢ'СҖавРҪРөРҪРҪРҫСҒСӮСҢ СҒРөРјСҸ'РҪ,РҫРҙРҪРҫСҖРҫРҙРҪРҫСҒСӮСҢ СҒРөРјСҸРҪ РҝРҫ РІРөлиСҮРёРҪРө (РҝСҖРөРёРјСғСүРөСҒСӮРІРөРҪРҪРҫ РҝРҫ СӮРҫР»СүРёРҪРө). РЎРөРјРөРҪРҪР°СҸ РҝР°СҖСӮРёСҸ РјРҫР¶РөСӮ РёРјРөСӮСҢ РІСӢСҒРҫРәРёР№ РІРөСҒ 1000 СҒРөРјСҸРҪ, РҪРҫ СҒРҫСҒСӮРҫСҸСӮСҢ РёР· РҪРөРҫРҙРҪРҫСҖРҫРҙРҪСӢС… РҝРҫ РІРөлиСҮРёРҪРө (РәСҖСғРҝРҪСӢС… Рё РјРөР»РәРёС…) СҒРөРјСҸРҪ, РҫРұлаРҙР°СҺСүРёС… СҖазРҪСӢРјРё РҝРҫСҒРөРІРҪСӢРјРё Рё СғСҖРҫжайРҪСӢРјРё РәР°СҮРөСҒСӮвами. РқРөРҫРұС…РҫРҙРёРјРҫ, СҮСӮРҫРұСӢ СҒРөРјРөРҪР° РёРјРөли РІСӢСҒРҫРәРёР№ РІРөСҒ 1000 СҲСӮСғРә Рё С…РҫСҖРҫСҲСғСҺ РІСӢСҖавРҪРөРҪРҪРҫСҒСӮСҢ (РҪРө РҪРёР¶Рө 80% РҙР»СҸ РәРҫРҪРҙРёСҶРёРҫРҪРҪСӢС… СҒРөРјСҸРҪ), СӮР°Рә РәР°Рә РҫСӮ СҚСӮРҫРіРҫ завиСҒРёСӮ СҖавРҪРҫРјРөСҖРҪРҫРө СҖазвиСӮРёРө РІСҒС…РҫРҙРҫРІ. Р’. СҒ. завиСҒРёСӮ РҫСӮ РҝСҖиёмРҫРІ РІСӢСҖР°СүРёРІР°РҪРёСҸ СҒРөРјРөРҪРҪРёРәРҫРІ, РјРөСӮРөРҫСҖРҫР»РҫРіРёСҮРөСҒРәРёС… фаРәСӮРҫСҖРҫРІ, СҒСӮСҖРҫРөРҪРёСҸ СҒРҫСҶРІРөСӮРёР№ Рё РҙСҖ. ДажРө РҝСҖРё С…РҫСҖРҫСҲРөРј СҖазвиСӮРёРё СҖР°СҒСӮРөРҪРёР№ РҪРөРІСӢСҖавРҪРөРҪРҪРҫСҒСӮСҢ СҒРөРјСҸРҪ СҒРҫС…СҖР°РҪСҸРөСӮСҒСҸ, СҮСӮРҫ РҫРұСғСҒР»РҫРІР»РөРҪРҫ СҖР°СҒРҝРҫР»РҫР¶РөРҪРёРөРј РёС… РІ СҒРҫСҶРІРөСӮРёРё. РўР°Рә, Сғ злаРәРҫРІ Р·РөСҖРҪРҫ РІ СҒСҖРөРҙРҪРөР№ СҮР°СҒСӮРё РәРҫР»РҫСҒР° РұРҫР»РөРө РәСҖСғРҝРҪРҫРө Рё СӮСҸР¶РөР»РҫРІРөСҒРҪРҫРө, СҮРөРј РІ РІРөСҖС…РҪРёС… Рё РҪРёР¶РҪРёС… СҮР°СҒСӮСҸС…. РһСҒРҫРұРҫРө Р·РҪР°СҮРөРҪРёРө Р’. СҒ. РёРјРөРөСӮ РҝСҖРё РіРҪРөР·РҙРҫРІСӢС… Рё РҝСғРҪРәСӮРёСҖРҪСӢС… РҝРҫСҒРөвах, РҝРҫСҚСӮРҫРјСғ РҝСҖРёРјРөРҪСҸСҺСӮ РәСғРәСғСҖСғР·СӢ Рё РҙСҖСғРіРёС… РәСғР»СҢСӮСғСҖ. РһСҮРёСҒСӮРәР° Рё СҒРҫСҖСӮРёСҖРҫРІР°РҪРёРө СҒРөРјСҸРҪ СӮР°РәР¶Рө СҒРҝРҫСҒРҫРұСҒСӮРІСғСҺСӮ РёС… РІСӢСҖавРҪРөРҪРҪРҫСҒСӮРё. Р’. СҒ. РҫРҝСҖРөРҙРөР»СҸСҺСӮ РіРҫСҒСғРҙР°СҖСҒСӮРІРөРҪРҪСӢРө СҒРөРјРөРҪРҪСӢРө РёРҪСҒРҝРөРәСҶРёРё РҝСҖРё РәРҫРҪСӮСҖРҫР»СҢРҪРҫ-СҒРөРјРөРҪРҪРҫРј Р°РҪализРө. РЎРөРјРөРҪР° СҖазРҙРөР»СҸСҺСӮ РҪР° С„СҖР°РәСҶРёРё РҝРҫ СҖазмРөСҖам, РІРөСҒСғ, Р°СҚСҖРҫРҙРёРҪамиСҮРөСҒРәРёРј СҒРІРҫР№СҒСӮвам, Рё СҒСғРјРјСғ РҙРІСғС… СҒРјРөР¶РҪСӢС… РҪаиРұРҫР»СҢСҲРёС… С„СҖР°РәСҶРёР№ РІСӢСҖажаСҺСӮ РІ РҝСҖРҫСҶРөРҪСӮах Рә РёСҒС…РҫРҙРҪРҫР№ РҪавРөСҒРәРө. В В Рң. Рҡ. РӨРёСҖСҒРҫРІР°. Р’СӢСҖавРҪРёРІР°РҪРёРө Р’СӢСҖР°'РІРҪРёРІР°РҪРёРөРІ СҒСӮР°СӮРёСҒСӮРёРәРө, РјРөСӮРҫРҙ, РҝСҖРё РҝРҫРјРҫСүРё РәРҫСӮРҫСҖРҫРіРҫ РҝРҫР»СғСҮР°СҺСӮ Р°РҪалиСӮРёСҮРөСҒРәРҫРө Рё РіСҖафиСҮРөСҒРәРҫРө РІСӢСҖажРөРҪРёРө СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРҫР№ Р·Р°РәРҫРҪРҫРјРөСҖРҪРҫСҒСӮРё, Р»РөжаСүРөР№ РІ РҫСҒРҪРҫРІРө Р·Р°РҙР°РҪРҪРҫРіРҫ СҚРјРҝРёСҖРёСҮРөСҒРәРҫРіРҫ СҖСҸРҙР° СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёС… РҙР°РҪРҪСӢС…. РҹСғСӮём Р’. Р»РҫРјР°РҪСғСҺ лиРҪРёСҺ СғСҖРҫРІРҪРөР№ СҚРјРҝРёСҖРёСҮРөСҒРәРҫРіРҫ СҖСҸРҙР° замРөРҪСҸСҺСӮ РҝлавРҪРҫР№ «вСӢСҖавРҪРёРІР°СҺСүРөР№В» РәСҖРёРІРҫР№ (РІ СҮР°СҒСӮРҪРҫРј СҒР»СғСҮР°Рө - РҝСҖСҸРјРҫР№) Рё РІСӢСҮРёСҒР»СҸСҺСӮ СғСҖавРҪРөРҪРёРө СҚСӮРҫР№ РәСҖРёРІРҫР№. РҹСҖРё Р’. РҝРҫСҒР»РөРҙРҫРІР°СӮРөР»СҢРҪРҫ СҖРөСҲР°СҺСӮ СӮСҖРё Р·Р°РҙР°СҮРё: РІСӢРұРёСҖР°СҺСӮ СӮРёРҝ СғСҖавРҪРөРҪРёСҸ (С„РҫСҖРјСғ РҝлавРҪРҫР№ РәСҖРёРІРҫР№); РІСӢСҮРёСҒР»СҸСҺСӮ РҝР°СҖамРөСӮСҖСӢ (РәРҫСҚффиСҶРёРөРҪСӮСӢ) СҚСӮРҫРіРҫ СғСҖавРҪРөРҪРёСҸ; РІСӢСҮРёСҒР»СҸСҺСӮ (РҪР° РҫСҒРҪРҫРІР°РҪРёРё СғСҖавРҪРөРҪРёСҸ) или РёР·РјРөСҖСҸСҺСӮ (РҝРҫ РіСҖафиРәСғ РәСҖРёРІРҫР№) СғСҖРҫРІРҪРё (РҫСҖРҙРёРҪР°СӮСӢ) РҝРҫР»СғСҮРөРҪРҪРҫРіРҫ В«СӮРөРҫСҖРөСӮРёСҮРөСҒРәРҫРіРҫВ» СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРҫРіРҫ СҖСҸРҙР°. РўРёРҝ СғСҖавРҪРөРҪРёСҸ Рё, СҒРҫРҫСӮРІРөСӮСҒСӮРІРөРҪРҪРҫ, С„РҫСҖРјСғ РҝлавРҪРҫР№ РәСҖРёРІРҫР№ РІСӢРұРёСҖР°СҺСӮ РҪР° РҫСҒРҪРҫРІР°РҪРёРё РҫРұСүРёС… СҒРІРөРҙРөРҪРёР№ (или СҮР°СҒСӮРҫ - РёР· РҝСҖР°РәСӮРёСҮРөСҒРәРҫРіРҫ РҫРҝСӢСӮР°) Рҫ СҒСғСүРҪРҫСҒСӮРё СҸРІР»РөРҪРёСҸ, Рҫ Р·Р°РәРҫРҪРҫРјРөСҖРҪРҫСҒСӮСҸС… РөРіРҫ СҒСӮСҖСғРәСӮСғСҖСӢ Рё СҖазвиСӮРёСҸ, Рҫ завиСҒРёРјРҫСҒСӮРё РјРөР¶РҙСғ РөРіРҫ РҝСҖРёР·РҪР°Рәами Рё СӮ.Рҙ. (СӮР°Рә РҪазСӢРІР°РөРјРҫРө «аРҪалиСӮРёСҮРөСҒРәРҫРөВ» Р’.); РҝСҖРё РҫСӮСҒСғСӮСҒСӮРІРёРё СӮР°РәРёС… РҝСҖРөРҙРІР°СҖРёСӮРөР»СҢРҪСӢС… СҒРІРөРҙРөРҪРёР№ СӮРёРҝ СғСҖавРҪРөРҪРёСҸ (С„РҫСҖРјСғ РәСҖРёРІРҫР№) СҮР°СҒСӮРҫ РјРҫР¶РөСӮ РҝРҫРҙСҒРәазаСӮСҢ РіСҖафиСҮРөСҒРәР°СҸ С„РҫСҖРјР° Р»РҫРјР°РҪРҫР№, РІСӢСҖажаСҺСүРөР№ Р·Р°РҙР°РҪРҪСӢР№ СҚРјРҝРёСҖРёСҮРөСҒРәРёР№ СҖСҸРҙ. В Р’ СҒРҫСҶиалСҢРҪРҫ-СҚРәРҫРҪРҫРјРёСҮРөСҒРәРҫР№ СҒСӮР°СӮРёСҒСӮРёРәРө Р’. РҝСҖРёРјРөРҪСҸСҺСӮ РІ СӮСҖёх СӮРёРҝРёСҮРҪСӢС… СҒР»СғСҮР°СҸС…: 1) Р’. СҖСҸРҙРҫРІ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёР№; 2) Р’. Р»РҫРјР°РҪСӢС… лиРҪРёР№ СҖРөРіСҖРөСҒСҒРёРё; 3) Р’. СҖСҸРҙРҫРІ РҙРёРҪамиРәРё. РҰРөР»СҢ Р’. СҖСҸРҙРҫРІ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ - РәРҫлиСҮРөСҒСӮРІРөРҪРҪРҫ Рё РіСҖафиСҮРөСҒРәРё РІСӢСҖазиСӮСҢ С…Р°СҖР°РәСӮРөСҖ Р·Р°РәРҫРҪРҫРјРөСҖРҪРҫСҒСӮРё СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ РөРҙРёРҪРёСҶ СҒРҫРІРҫРәСғРҝРҪРҫСҒСӮРё РҝРҫ РҙР°РҪРҪРҫРјСғ РҝСҖРёР·РҪР°РәСғ (РҪР°РҝСҖРёРјРөСҖ, РёС… РҪРҫСҖмалСҢРҪРҫРө СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёРө, СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёРө РҝРҫ Р·Р°РәРҫРҪСғ РҹСғР°СҒСҒРҫРҪР° Рё СӮ.Рҝ.). РҹСҖРё СҚСӮРҫРј СҒРҫС…СҖР°РҪСҸСҺСӮ СҖавРөРҪСҒСӮРІРҫ РҪРөРәРҫСӮРҫСҖСӢС… главРҪСӢС… СҮРёСҒР»РҫРІСӢС… С…Р°СҖР°РәСӮРөСҖРёСҒСӮРёРә Р·Р°РҙР°РҪРҪРҫРіРҫ СҚРјРҝРёСҖРёСҮРөСҒРәРҫРіРҫ Рё РҝРҫР»СғСҮР°РөРјРҫРіРҫ СӮРөРҫСҖРөСӮРёСҮРөСҒРәРҫРіРҫ СҖСҸРҙРҫРІ: СҒСҖРөРҙРҪРөР№ РІРөлиСҮРёРҪСӢ РҝСҖРёР·РҪР°РәР°, СҒСҖРөРҙРҪРөРіРҫ РәРІР°РҙСҖР°СӮРёСҮРөСҒРәРҫРіРҫ РҫСӮРәР»РҫРҪРөРҪРёСҸ, РҫРұСүРөР№ СҮРёСҒР»РөРҪРҪРҫСҒСӮРё РөРҙРёРҪРёСҶ СҒРҫРІРҫРәСғРҝРҪРҫСҒСӮРё. РЎСӮРөРҝРөРҪСҢ СҒРҫРІРҫРәСғРҝРҪРҫРіРҫ СҒРҫРҫСӮРІРөСӮСҒСӮРІРёСҸ СғСҖРҫРІРҪРөР№ (РҫСҖРҙРёРҪР°СӮ) РҝРҫР»СғСҮРөРҪРҪРҫРіРҫ СӮРөРҫСҖРөСӮРёСҮРөСҒРәРҫРіРҫ СҖСҸРҙР° СғСҖРҫРІРҪСҸРј СҚРјРҝРёСҖРёСҮРөСҒРәРёРј РІСӢСҸСҒРҪСҸСҺСӮ РҝСҖРё РҝРҫРјРҫСүРё РәР°РәРҫРіРҫ-лиРұРҫ РәСҖРёСӮРөСҖРёСҸ СҒРҫглаСҒРёСҸ. Р’ РҪРөРәРҫСӮРҫСҖСӢС… РҫСҒРҫРұСӢС… СҒР»СғСҮР°СҸС… - РҪР°РҝСҖРёРјРөСҖ, РҝСҖРё Р’. СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёСҸ РҪР°СҒРөР»РөРҪРёСҸ РҝРҫ РІРҫР·СҖР°СҒСӮСғ, РҝРҫРәазаРҪРҪРҫРјСғ РҝСҖРё РҝРөСҖРөРҝРёСҒРё, РҙР»СҸ СғСҒСӮСҖР°РҪРөРҪРёСҸ С…РҫСҖРҫСҲРҫ РёР·РІРөСҒСӮРҪРҫР№ «аРәРәСғРјСғР»СҸСҶРёРё РІРҫР·СҖР°СҒСӮРҫРІВ», РҫРәР°РҪСҮРёРІР°СҺСүРёС…СҒСҸ РҪР° 0 или РҪР° 5, - РҝСҖРёРјРөРҪСҸСҺСӮ СҒРҝРөСҶиалСҢРҪРҫ СҖазСҖР°РұРҫСӮР°РҪРҪСӢРө СҒРҝРҫСҒРҫРұСӢ Рё С„РҫСҖРјСғР»СӢ. Р’. СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёР№ РІСҒРөРіРҙР° РҝСҖРөРҙРҝРҫлагаРөСӮ РҪалиСҮРёРө РҙРҫСҒСӮР°СӮРҫСҮРҪРҫ РјРҪРҫРіРҫСҮРёСҒР»РөРҪРҪРҫРіРҫ Р·Р°РҙР°РҪРҪРҫРіРҫ СҚРјРҝРёСҖРёСҮРөСҒРәРҫРіРҫ СҖСҸРҙР° РҙР°РҪРҪСӢС…. Р’. Р»РҫРјР°РҪСӢС… лиРҪРёР№ СҖРөРіСҖРөСҒСҒРёРё РҝСҖРҫРёР·РІРҫРҙСҸСӮ РҝСҖРё РёР·СғСҮРөРҪРёРё СҒРІСҸР·РөР№ РҝСҖРёР·РҪР°РәРҫРІ, СҮСӮРҫРұСӢ РҝРҫР»СғСҮРёСӮСҢ РҝлавРҪСғСҺ лиРҪРёСҺ СҖРөРіСҖРөСҒСҒРёРё Рё СғСҖавРҪРөРҪРёРө СҖРөРіСҖРөСҒСҒРёРё (РәРҫСҖСҖРөР»СҸСҶРёРҫРҪРҪРҫРө), РІСӢСҖажаСҺСүРөРө завиСҒРёРјРҫСҒСӮСҢ СҒСҖРөРҙРҪРёС… Р·РҪР°СҮРөРҪРёР№ РҫРҙРҪРҫРіРҫ РҝСҖРёР·РҪР°РәР° РҫСӮ Р·РҪР°СҮРөРҪРёР№ РҙСҖСғРіРёС…, РҪР°РҝСҖРёРјРөСҖ:
В РӣРёСӮ.:РҘС‘РҪСӮРёРҪРіСӮРҫРҪ Р•. Р’., Р’СӢСҖавРҪРёРІР°РҪРёРө РәСҖРёРІСӢС… РҝРҫ СҒРҝРҫСҒРҫРұСғ РҪаимРөРҪСҢСҲРёС… РәРІР°РҙСҖР°СӮРҫРІ Рё СҒРҝРҫСҒРҫРұСғ РјРҫРјРөРҪСӮРҫРІ, РІ РәРҪ.: РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёРө РјРөСӮРҫРҙСӢ РІ СҒСӮР°СӮРёСҒСӮРёРәРө. РЎРұ. СҒСӮР°СӮРөР№, РҝРҫРҙ СҖРөРҙ. Р“. Рӣ. Р РёСӮСҶР°. РҹРөСҖ. Рё РҫРұСҖР°Рұ. РЎ. Рҹ. Р‘РҫРұСҖРҫРІР°, Рң., 1927, СҒ. 147-61; ЕжРҫРІ Рҗ. Рҳ., Р’СӢСҖавРҪРёРІР°РҪРёРө Рё РІСӢСҮРёСҒР»РөРҪРёРө СҖСҸРҙРҫРІ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёР№, Рң., 1961; РҘРҫСӮРёРјСҒРәРёР№ Р’. Рҳ., Р’СӢСҖавРҪРёРІР°РҪРёРө СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёС… СҖСҸРҙРҫРІ РҝРҫ РјРөСӮРҫРҙСғ РҪаимРөРҪСҢСҲРёС… РәРІР°РҙСҖР°СӮРҫРІ (СҒРҝРҫСҒРҫРұ Р§РөРұСӢСҲРөРІР°), Рң. - Рӣ., 1925, 2 РёР·Рҙ., Рң., 1959; Р§РөСӮРІРөСҖРёРәРҫРІ Рқ. РЎ., Рһ СӮРөС…РҪРёРәРө РІСӢСҮРёСҒР»РөРҪРёСҸ РҝР°СҖР°РұРҫлиСҮРөСҒРәРёС… РәСҖРёРІСӢС…, РІ СҒРұ.: Р’РҫРҝСҖРҫСҒСӢ РәРҫРҪСҠСҺРҪРәСӮСғСҖСӢ, СӮ. 2, Рң., 1926; РҝРөСҖРөРёР·Рҙ. РІ РөРіРҫ РәРҪ.: РЎСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёРө Рё СҒС…РҫлаСҒСӮРёСҮРөСҒРәРёРө РёСҒСҒР»РөРҙРҫРІР°РҪРёСҸ, Рң., 1963, СҒ. 190-210; РҜСҒСӮСҖРөРјСҒРәРёР№ Р‘. РЎ., РқРөРәРҫСӮРҫСҖСӢРө РІРҫРҝСҖРҫСҒСӢ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ СҒСӮР°СӮРёСҒСӮРёРәРё, Рң., 1961, РіР». II; РһРұСғС…РҫРІ Р’. Рң., Рҡ РІРҫРҝСҖРҫСҒСғ Рҫ РҪахРҫР¶РҙРөРҪРёРё СғСҖавРҪРөРҪРёСҸ СҖРөРіСҖРөСҒСҒРёРё, СғРҙРҫРІР»РөСӮРІРҫСҖСҸСҺСүРөРіРҫ РҙР°РҪРҪРҫРјСғ СҚРјРҝРёСҖРёСҮРөСҒРәРҫРјСғ СҖСҸРҙСғ, «ТСҖСғРҙСӢ РҰРЎРЈВ», СӮ. 16, РІ. II, Рң., 1923. В РӨ. Р”. РӣРёРІСҲРёСҶ. Р’СӢСҖазиСӮРөР»СҢРҪСӢРө РҙРІРёР¶РөРҪРёСҸ Р’СӢСҖази'СӮРөР»СҢРҪСӢРө РҙРІРёР¶Рө'РҪРёСҸ,РҙРІРёР¶РөРҪРёСҸ, РҝСҖРҫСҸРІР»СҸСҺСүРёРөСҒСҸ РҝСҖРё СҖазлиСҮРҪСӢС… (РҫСҒРҫРұРөРҪРҪРҫ СҚРјРҫСҶРёРҫРҪалСҢРҪСӢС…) РҝСҒРёС…РёСҮРөСҒРәРёС… СҒРҫСҒСӮРҫСҸРҪРёСҸС… Рё СҒР»СғжаСүРёРө РёС… РІРҪРөСҲРҪРёРј РІСӢСҖажРөРҪРёРөРј. СамСӢР№ Р·РҪР°СҮРёСӮРөР»СҢРҪСӢР№ РәлаСҒСҒ Р’. Рҙ. РҝСҖРөРҙСҒСӮавлРөРҪ РІ Рё . Р’ РұРҫР»РөРө СҲРёСҖРҫРәРҫРј РҝРҫРҪРёРјР°РҪРёРё Р’. Рҙ. РІРәР»СҺСҮР°СҺСӮ РІСҒРө РҫСӮСӮРөРҪРәРё РіРҫР»РҫСҒР° Рё РёРҪСӮРҫРҪР°СҶРёРё, РҝРөСҖРөРҙР°СҺСүРёРө СҚРјРҫСҶРёРё, Р° СӮР°РәР¶Рө РІРөРіРөСӮР°СӮРёРІРҪСӢРө СҖРөР°РәСҶРёРё, СҒРҫРҝСҖРҫРІРҫР¶РҙР°СҺСүРёРө СҚСӮРё СҚРјРҫСҶРёРё, - СҒРҫСҒСғРҙРёСҒСӮСӢРө, РҙСӢС…Р°СӮРөР»СҢРҪСӢРө, СҒРөРәСҖРөСӮРҫСҖРҪСӢРө. В РҹСҖР°РәСӮРёСҮРөСҒРәРёРө РҝСҖРөРҙСҒСӮавлРөРҪРёСҸ Рҫ Р’. Рҙ. СғР¶Рө РІ РҙСҖРөРІРҪРҫСҒСӮРё РёСҒРҝРҫР»СҢР·РҫвалиСҒСҢ РІ Р°РәСӮС‘СҖСҒРәРҫРј Рё РҫСҖР°СӮРҫСҖСҒРәРҫРј РёСҒРәСғСҒСҒСӮРІРө, Р° СӮР°РәР¶Рө РІ РҝРөСҖРІСӢС… РҝРҫРҝСӢСӮРәах РҝРҫСҒСӮСҖРҫРөРҪРёСҸ . РҹРҫРҙСҖРҫРұРҪСӢРө РҫРҝРёСҒР°РҪРёСҸ Р’. Рҙ. РҝРҫСҸвилиСҒСҢ РІ 17 РІ., Р° СҒРёСҒСӮРөРјР°СӮРёСҮРөСҒРәРҫРө РёСҒСҒР»РөРҙРҫРІР°РҪРёРө РёС… РҪР°СҮалРҫСҒСҢ РІ 18 РІ. (РҫРҝРёСҒР°РҪРёРө Р°РҪР°СӮРҫРјРёСҮРөСҒРәРёС… РҫСҒРҫРұРөРҪРҪРҫСҒСӮРөР№ Р’. Рҙ., С…Р°СҖР°РәСӮРөСҖРҪСӢС… РҙР»СҸ СҖазлиСҮРҪСӢС… РҙСғСҲРөРІРҪСӢС… СҒРҫСҒСӮРҫСҸРҪРёР№). Р—РҪР°СҮРёСӮРөР»СҢРҪСӢР№ СҚСӮР°Рҝ РІ СҖазвиСӮРёРё РҪР°СғСҮРҪСӢС… РҝСҖРөРҙСҒСӮавлРөРҪРёР№ Рҫ Р’. Рҙ. СҒРҫСҒСӮавили СҖР°РұРҫСӮСӢ Р°РҪглийСҒРәРҫРіРҫ СғСҮРөРҪРҫРіРҫ Р§. Р‘Рөлла, РІ РәРҫСӮРҫСҖСӢС… РұСӢла РҝРҫРәазаРҪР° СҒРІСҸР·СҢ Р’. Рҙ. СҒ С„СғРҪРәСҶРёСҸРјРё СҖазлиСҮРҪСӢС… РҫСӮРҙРөР»РҫРІ РҪРөСҖРІРҪРҫР№ СҒРёСҒСӮРөРјСӢ. РҹСҖРҫРұР»РөРјР° РҝСҖРҫРёСҒС…РҫР¶РҙРөРҪРёСҸ Р’. Рҙ. РұСӢла РІРҝРөСҖРІСӢРө РҝРҫСҒСӮавлРөРҪР° Р“. РЎРҝРөРҪСҒРөСҖРҫРј, СҖазвиСӮР° Рҳ. Рң. РЎРөСҮРөРҪРҫРІСӢРј. РӯСӮР° РҝСҖРҫРұР»РөРјР° РҝРҫР»СғСҮила СҒРІРҫСҺ РІСҒРөСҒСӮРҫСҖРҫРҪРҪСҺСҺ СҖазСҖР°РұРҫСӮРәСғ РІ СӮСҖСғРҙах Р§. ДаСҖРІРёРҪР°, РІ СҒС„РҫСҖРјСғлиСҖРҫРІР°РҪРҪСӢС… РёРј СӮСҖёх РҝСҖРёРҪСҶРёРҝах: РҝСҖРёРҪСҶРёРҝРө РҝРҫР»РөР·РҪСӢС… Р°СҒСҒРҫСҶРёРёСҖРҫРІР°РҪРҪСӢС… РҝСҖРёРІСӢСҮРөРә (Р’. Рҙ. РәР°Рә РҝСҖРҫРҙСғРәСӮ СғРҪР°СҒР»РөРҙРҫРІР°РҪРҪСӢС… Р°СҒСҒРҫСҶРёР°СҶРёР№ РјРөР¶РҙСғ РҫРҝСҖРөРҙРөлёРҪРҪСӢРјРё РҫСүСғСүРөРҪРёСҸРјРё Рё СҚРјРҫСҶРёСҸРјРё Рё РёС… РІРҪРөСҲРҪРёРј РҝСҖРҫСҸРІР»РөРҪРёРөРј), РҝСҖРёРҪСҶРёРҝРө Р°РҪСӮРёСӮРөР·СӢ, РҙРөР№СҒСӮРІСғСҺСүРөРј РҝСҖРё РҝСҖРҫСӮРёРІРҫРҝРҫР»РҫР¶РҪСӢС… СҚРјРҫСҶРёСҸС… (РҪР°РҝСҖРёРјРөСҖ, РҪР°РҝСҖСҸжёРҪРҪР°СҸ РҝРҫР·Р° СҖазгРҪРөРІР°РҪРҪРҫР№ СҒРҫРұР°РәРё СҒРјРөРҪСҸРөСӮСҒСҸ РҝРҫР·РҫР№ РҝРҫРәРҫСҖРҪРҫСҒСӮРё Рё СҖР°СҒСҒлаРұР»РөРҪРёРөРј РјСӢСҲСҶ РҝСҖРё РІСҒСӮСҖРөСҮРө СҒ С…РҫР·СҸРёРҪРҫРј), Рё РҝСҖРёРҪСҶРёРҝРө РҫРұСүРөРіРҫ РІРҫР·РұСғР¶РҙРөРҪРёСҸ РҪРөСҖРІРҪРҫР№ СҒРёСҒСӮРөРјСӢ (Р’. Рҙ., СҒРІСҸР·Р°РҪРҪСӢРө СҒ РұСғСҖРҪСӢРјРё СҚРјРҫСҶРёСҸРјРё или РІСҒРҝСӢСҲРәами аффРөРәСӮР°). РӯРІРҫР»СҺСҶРёРҫРҪРҪСӢРө РёРҙРөРё ДаСҖРІРёРҪР° РұСӢли СҖазвиСӮСӢ СҖСғСҒСҒРәРёРјРё РҝСҒРёС…РҫР»Рҫгами (Рҹ. РӨ. РӣРөСҒгафСӮРҫРј, Р’. Рң. Р‘РөС…СӮРөСҖРөРІСӢРј Рё РҙСҖ.), РҝРҫРҙСҮРөСҖРәРҪСғРІСҲРёРјРё, РІ СҮР°СҒСӮРҪРҫСҒСӮРё, СҖРҫР»СҢ РІРҫСҒРҝРёСӮР°РҪРёСҸ Рё СҒСҖРөРҙСӢ РІ С„РҫСҖРјРёСҖРҫРІР°РҪРёРё Р’. Рҙ. СҖРөРұС‘РҪРәР°. РўРөРј СҒамСӢРј РұРёРҫР»РҫРіРёСҮРөСҒРәРёР№ Р°СҒРҝРөРәСӮ РёР·СғСҮРөРҪРёСҸ Р’. Рҙ. РұСӢР» РҙРҫРҝРҫР»РҪРөРҪ СҒРҫСҶиалСҢРҪСӢРј. В Р’ 20 РІ. РҫРұСҠРөРәСӮРҫРј РёСҒСҒР»РөРҙРҫРІР°РҪРёСҸ СҒСӮали Р’. Рҙ. РҪРө СӮРҫР»СҢРәРҫ Сғ СҮРөР»РҫРІРөРәР° Рё РІСӢСҒСҲРёС… живРҫСӮРҪСӢС…, РҪРҫ Рё Сғ СҮР»РөРҪРёСҒСӮРҫРҪРҫРіРёС…, СҖСӢРұ, РҝСӮРёСҶ (СҚСӮРё РёСҒСҒР»РөРҙРҫРІР°РҪРёСҸ РҫСҒРҫРұРөРҪРҪРҫ СҲРёСҖРҫРәРҫ РҝСҖРҫРІРҫРҙСҸСӮСҒСҸ РІ СҖамРәах ). РқРҫРІСӢРө Р°СҒРҝРөРәСӮСӢ Р’. Рҙ. СҖР°СҒРәСҖСӢСӮСӢ РІ СҒРІСҸР·Рё СҒ СҖазвиСӮРёРөРј СҒРөРјРёРҫСӮРёРәРё; РІ СҮР°СҒСӮРҪРҫСҒСӮРё, РІ РёР·СғСҮР°СҺСӮСҒСҸ С„СғРҪРәСҶРёРё СҖСҸРҙР° Р’. Рҙ. РІ РҝСҖРҫСҶРөСҒСҒРө РәРҫРјРјСғРҪРёРәР°СҶРёРё. В РӣРёСӮ.:Р’СғРҙРІРҫСҖСӮСҒ Р ., РӯРәСҒРҝРөСҖРёРјРөРҪСӮалСҢРҪР°СҸ РҝСҒРёС…РҫР»РҫРіРёСҸ, РҝРөСҖ. СҒ Р°РҪРіР»., Рң., 1950; РҜРәРҫРұСҒРҫРҪ Рҹ. Рң., РҹСҒРёС…РҫР»РҫРіРёСҸ СҮСғРІСҒСӮРІ, 2 РёР·Рҙ., Рң., 1958. В РЎ. Р“. Р“РөллРөСҖСҲСӮРөР№РҪ. Р’СӢСҖР°СҒСӮРҪРҫР№ РҝСҖСғРҙ Р’СӢСҖР°СҒСӮРҪРҫ'Р№ РҝСҖСғРҙ,Р»РөСӮРҪРёР№ РҝСҖСғРҙ РҙР»СҸ РІСӢСҖР°СүРёРІР°РҪРёСҸ РҝРөСҖРөСҒаживаРөРјСӢС… РёР· РҪРөСҖРөСҒСӮРҫРІСӢС… или СҖР°СҒСҒР°РҙРҪСӢС… РҝСҖСғРҙРҫРІ малСҢРәРҫРІ РҙРҫ СҒСӮР°РҙРёРё СҒРөРіРҫР»РөСӮРәРҫРІ. РҹР»РҫСүР°РҙСҢ 5-10 (РҙРҫ 20) РіР°, СҒ С…РҫСҖРҫСҲРөР№ РҝР»РҫРҙРҫСҖРҫРҙРҪРҫР№ РҝРҫСҮРІРҫР№. РЎСҖРөРҙРҪСҸСҸ РіР»СғРұРёРҪР° 60-80 СҒРј, Сғ РІРҫРҙРҫСҒРҝСғСҒРәР° 1,5 Рј. РқР°РҝРҫР»РҪРөРҪРёРө РІРҫРҙРҫР№ 10 СҒСғСӮРҫРә, СҒРұСҖРҫСҒ РІРҫРҙСӢ РҪРө РұРҫР»РөРө 5-10 СҒСғСӮРҫРә. Р–РөлаСӮРөР»РөРҪ РҝРҫСҒСӮРҫСҸРҪРҪСӢР№ РҝСҖРёСӮРҫРә РІРҫРҙСӢ. РЎРј. . Р’СӢСҖРіР°РҪ РҳРІР°РҪ РҗРҪРёРәРөРөРІРёСҮ Р’СӢСҖРіР°'РҪРҳРІР°РҪ РҗРҪРёРәРөРөРІРёСҮ [СҖ. 19.5 (1.6).1908, СҒ. РңР°СӮРІРөРөРІРәР° РҪР° РҹРҫР»СӮавСүРёРҪРө], СғРәСҖаиРҪСҒРәРёР№ СҒРҫРІРөСӮСҒРәРёР№ РҝРҫСҚСӮ. Р РҫРҙРёР»СҒСҸ РІ РәСҖРөСҒСӮСҢСҸРҪСҒРәРҫР№ СҒРөРјСҢРө. РһРәРҫРҪСҮРёР» филРҫР»РҫРіРёСҮРөСҒРәРёР№ фаРәСғР»СҢСӮРөСӮ РҘР°СҖСҢРәРҫРІСҒРәРҫРіРҫ СғРҪРёРІРөСҖСҒРёСӮРөСӮР° РІ 1940. РЈСҮР°СҒСӮРҪРёРә Р’РөлиРәРҫР№ РһСӮРөСҮРөСҒСӮРІРөРҪРҪРҫР№ РІРҫР№РҪСӢ. РҹРөСҖРІР°СҸ РәРҪРёРіР° СҒСӮРёС…РҫРІ «ВРҫРҫСҖСғжёРҪРҪР°СҸ лиСҖРёРәа» РІСӢСҲла РІ 1934. Р’. - РҝРөРІРөСҶ РҪРҫРІРҫР№ СҒРҫСҶиалиСҒСӮРёСҮРөСҒРәРҫР№ РЈРәСҖаиРҪСӢ, РәРҫлхРҫР·РҪРҫРіРҫ СҒРөла, РҙСҖСғР¶РұСӢ РҪР°СҖРҫРҙРҫРІ. Р’ РҝРҫСҒР»РөРІРҫРөРҪРҪСӢРө РіРҫРҙСӢ РІСӢСҒСӮСғРҝал СӮР°РәР¶Рө РәР°Рә РҪРҫРІРөллиСҒСӮ Рё РҝРөСҖРөРІРҫРҙСҮРёРә. В РЎРҫСҮ.: Р’РёСҖРіР°РҪ I., Р’РёРұСҖР°РҪРө, Рҡ., 1956; Р’ СҖРҫР·РҝРҫРІРҪi Р»iСӮР°, РҘР°СҖ., 1959; РқР°Рҙ РЎСғР»РҫСҺ СҲСғРјР»СҸСӮСҢ СҸРІРҫСҖРё, Рҡ., 1960; РҹРёСӮРёРјРө Р·iллСҸ, Рҡ., 1967; Р’РёРұСҖР°РҪРө. РҹРҫРөР·ii. РҹРҫРөРјРё. РһРҝРҫРІiРҙР°РҪРҪСҸ. РҹРөСҖРөРәлаРҙРё, Рҡ., 1969; РІ СҖСғСҒ. РҝРөСҖ. - РҰРІРөСӮСғСүРёРө РұРөСҖРөРіР°, Рӣ., 1956; РҹРҫРІРҫСҖРҫСӮ СҒРҫР»РҪСҶР°. РЎСӮРёС…Рё Рё РҝРҫСҚРјР°, Рң., 1961. В РӣРёСӮ.:БаСҖР°РұР°СҲ Р®., БагаСӮСҒСӮРІРҫ СӮРІРҫСҖСҮРҫРҝ iРҪРҙРёРІiРҙСғалСҢРҪРҫСҒСӮi, РІ РөРіРҫ РәРҪ.: РҹРҫРөСӮ i СҮР°СҒ, Рҡ., 1958; РҹСҢСҸРҪРҫРІ Р’., IРІР°РҪ Р’РёСҖРіР°РҪ, РІ РәРҪ.: РЈРәСҖР°РҝРҪСҒСҢРәi СҖР°РҙСҸРҪСҒСҢРәРё РҝРёСҒСҢРјРөРҪРҪРёРәРё, РІ. 4, Рҡ., 1960. В РЎ. Рҗ. РҡСҖСӢжаРҪРҫРІСҒРәРёР№. Р’СӢСҖРөР·СғРұ Р’СӢСҖРөР·Сғ'Рұ(Rutilus frisii) СҖСӢРұР° СҒРөРјРөР№СҒСӮРІР° РәР°СҖРҝРҫРІСӢС…. ДлиРҪР° СӮРөла РҙРҫ 75 СҒРј, РІРөСҒРёСӮ РҙРҫ 6 РәРі. Р Р°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪР° РІ РұР°СҒСҒРөР№РҪах ЧёСҖРҪРҫРіРҫ Рё РҗР·РҫРІСҒРәРҫРіРҫ РјРҫСҖРөР№, РёР· СғСҒСӮСҢСҸ РҝРҫРҙРҪРёРјР°РөСӮСҒСҸ РҝРҫ СҖРөРәам РІСӢСҒРҫРәРҫ РІРІРөСҖС…. РҳРәСҖСғ РјРөСҮРөСӮ РІРҫ 2-Р№ РҝРҫР»РҫРІРёРҪРө РјР°СҸ РҪР° РәамРөРҪРёСҒСӮСӢС… СғСҮР°СҒСӮРәах СҖРөРәРё СҒ РұСӢСҒСӮСҖРҫР№ Рё СҮРёСҒСӮРҫР№ РІРҫРҙРҫР№ Рё РәамРөРҪРёСҒСӮСӢРј РҙРҪРҫРј. РҹРёСӮР°РөСӮСҒСҸ главРҪСӢРј РҫРұСҖазРҫРј РҙРҫРҪРҪСӢРјРё РјРҫллСҺСҒРәами, СҖР°РәРҫРІРёРҪСӢ РәРҫСӮРҫСҖСӢС… СҖазРҙавливаРөСӮ РјРҫСүРҪСӢРјРё РіР»РҫСӮРҫСҮРҪСӢРјРё Р·СғРұами. Р’ РұР°СҒСҒРөР№РҪРө РҡР°СҒРҝРёР№СҒРәРҫРіРҫ РјРҫСҖСҸ РҫРұРёСӮР°РөСӮ РҫСҒРҫРұСӢР№ РҝРҫРҙРІРёРҙ - . Р’. - СҶРөРҪРҪР°СҸ РҝСҖРҫРјСӢСҒР»РҫРІР°СҸ СҖСӢРұР°. ЧиСҒР»РөРҪРҪРҫСҒСӮСҢ РҪРөРІРөлиРәР° Рё РҝСҖРҫРҙРҫлжаРөСӮ СҒРҫРәСҖР°СүР°СӮСҢСҒСҸ РёР·-Р·Р° РҪРөРұлагРҫРҝСҖРёСҸСӮРҪСӢС… СғСҒР»РҫРІРёР№ РІРҫСҒРҝСҖРҫРёР·РІРҫРҙСҒСӮРІР°. Р’СӢСҖРёСҶР° Р’СӢ'СҖРёСҶР°,РҝРҫСҒРөР»РҫРә РіРҫСҖРҫРҙСҒРәРҫРіРҫ СӮРёРҝР° РІ ГаСӮСҮРёРҪСҒРәРҫРј СҖайРҫРҪРө РӣРөРҪРёРҪРіСҖР°РҙСҒРәРҫР№ РҫРұлаСҒСӮРё Р РЎРӨРЎР . Р Р°СҒРҝРҫР»РҫР¶РөРҪ Сғ РҝРөСҖРөСҒРөСҮРөРҪРёСҸ СҖ. РһСҖРөРҙРөР¶ (РҝСҖРёСӮРҫРә РӣСғРіРё) Р¶РөР»РөР·РҪРҫР№ РҙРҫСҖРҫРіРҫР№ РӣРөРҪРёРҪРіСҖР°Рҙ - Р’РөлиРәРёРө РӣСғРәРё, РІ 60 РәРјРә Р®. РҫСӮ РӣРөРҪРёРҪРіСҖР°РҙР°. 13,8 СӮСӢСҒ. жиСӮРөР»РөР№ (1968). ЗавРҫРҙСӢ: РҫРҝСӢСӮРҪРҫ-РјРөС…Р°РҪРёСҮРөСҒРәРёР№, РјРөСӮаллРҫРёР·РҙРөлий, РәРёСҖРҝРёСҮРҪСӢР№; Р»РөСҒРҫРјРөРұРөР»СҢРҪСӢР№ РәРҫРјРұРёРҪР°СӮ. Р’СӢСҖРҫРҙРәРҫРІ РҳРІР°РҪ Р“СҖРёРіРҫСҖСҢРөРІРёСҮ Р’СӢ'СҖРҫРҙРәРҫРІРҳРІР°РҪ Р“СҖРёРіРҫСҖСҢРөРІРёСҮ (СғРјРөСҖ РҫРәРҫР»Рҫ 1563 или 1564), СҖСғСҒСҒРәРёР№ РІРҫРөРҪРҪСӢР№ РёРҪР¶РөРҪРөСҖ, РёРјРөР» СҮРёРҪ РҙСҢСҸРәР°. РЈРҝРҫРјРёРҪР°РөСӮСҒСҸ РІ РёСҒСӮРҫСҮРҪРёРәах СҒ 1538. РЈСҮР°СҒСӮРІРҫвал РІ РҝРҫС…РҫРҙах РҪР° РҡазаРҪСҢ, РІ 1551 РҝРҫСҒСӮСҖРҫРёР» РҝРҫРҙ РҡазаРҪСҢСҺ Р·Р° 28 РҙРҪРөР№ РҙРөСҖРөРІСҸРҪРҪСғСҺ РәСҖРөРҝРҫСҒСӮСҢ РЎРІРёСҸР¶СҒРә, РҝРҫСҒР»СғживСҲСғСҺ РҫРҝРҫСҖРҪСӢРј РҝСғРҪРәСӮРҫРј РҙР»СҸ РІР·СҸСӮРёСҸ РіРҫСҖРҫРҙР° СҖСғСҒСҒРәРёРјРё. Р’ 1552 РҝСҖРё СҲСӮСғСҖРјРө РҡазаРҪРё СҖСғРәРҫРІРҫРҙРёР» С„РҫСҖСӮифиРәР°СҶРёРҫРҪРҪСӢРјРё СҖР°РұРҫСӮами Рё СҒРҫРҫСҖСғРҙРёР» 13-РјРөСӮСҖРҫРІСғСҺ РҫСҒР°РҙРҪСғСҺ РұР°СҲРҪСҺ, СҒРҫРұСҖР°РҪРҪСғСҺ Р·Р° РҫРҙРҪСғ РҪРҫСҮСҢ. Р’ 1557 РҝРҫСҒСӮСҖРҫРёР» РәСҖРөРҝРҫСҒСӮСҢ Рё гаваРҪСҢ РҝСҖРё СғСҒСӮСҢРө СҖ. РқР°СҖРІСӢ Рё РәСҖРөРҝРҫСҒСӮСҢ РІ ГалиСҮРө. Р’ 1563 РІ РҝРҫС…РҫРҙРө РҝРҫРҙ РҹРҫР»РҫСҶРә Р’. РәРҫРјР°РҪРҙРҫвал . РҡазРҪС‘РҪ РҝРҫ РҪРөРёР·РІРөСҒСӮРҪСӢРј РҝСҖРёСҮРёРҪам. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34 |
|||||||
 В Рё СӮ.Рҝ. Рҡ Р’. СҖСҸРҙРҫРІ РҙРёРҪамиРәРё РҝСҖРёРұРөРіР°СҺСӮ, СҮСӮРҫРұСӢ РҝРҫР»СғСҮРёСӮСҢ СғСҖавРҪРөРҪРёРө (Рё РҝлавРҪСғСҺ лиРҪРёСҺ), РІСӢСҖажаСҺСүРөРө СӮРөРҪРҙРөРҪСҶРёСҺ СҖазвиСӮРёСҸ РҝСҖРҫСҶРөСҒСҒР° РІРҫ РІСҖРөРјРөРҪРё (
t), РҪР°РҝСҖРёРјРөСҖ:
y=
a+
bt,
y=
a+
bt+
ct
2Рё СӮ.Рҝ. Р’ РҫРұРҫРёС… РҝРҫСҒР»РөРҙРҪРёС… СҒР»СғСҮР°СҸС… Р’. РәРҫСҚффиСҶРёРөРҪСӮСӢ
Р°,
РІ,
СҒ,... РёСҒРәРҫРјРҫРіРҫ СғСҖавРҪРөРҪРёСҸ РҫРұСӢСҮРҪРҫ РІСӢСҮРёСҒР»СҸСҺСӮ РҝРҫ
. РқРө СҒР»РөРҙСғРөСӮ СҒРјРөСҲРёРІР°СӮСҢ Р’. СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёС… СҖСҸРҙРҫРІ РҙРёРҪамиРәРё СҒРҫ СҒглаживаРҪРёРөРј СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёС… СҖСҸРҙРҫРІ.
В Рё СӮ.Рҝ. Рҡ Р’. СҖСҸРҙРҫРІ РҙРёРҪамиРәРё РҝСҖРёРұРөРіР°СҺСӮ, СҮСӮРҫРұСӢ РҝРҫР»СғСҮРёСӮСҢ СғСҖавРҪРөРҪРёРө (Рё РҝлавРҪСғСҺ лиРҪРёСҺ), РІСӢСҖажаСҺСүРөРө СӮРөРҪРҙРөРҪСҶРёСҺ СҖазвиСӮРёСҸ РҝСҖРҫСҶРөСҒСҒР° РІРҫ РІСҖРөРјРөРҪРё (
t), РҪР°РҝСҖРёРјРөСҖ:
y=
a+
bt,
y=
a+
bt+
ct
2Рё СӮ.Рҝ. Р’ РҫРұРҫРёС… РҝРҫСҒР»РөРҙРҪРёС… СҒР»СғСҮР°СҸС… Р’. РәРҫСҚффиСҶРёРөРҪСӮСӢ
Р°,
РІ,
СҒ,... РёСҒРәРҫРјРҫРіРҫ СғСҖавРҪРөРҪРёСҸ РҫРұСӢСҮРҪРҫ РІСӢСҮРёСҒР»СҸСҺСӮ РҝРҫ
. РқРө СҒР»РөРҙСғРөСӮ СҒРјРөСҲРёРІР°СӮСҢ Р’. СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёС… СҖСҸРҙРҫРІ РҙРёРҪамиРәРё СҒРҫ СҒглаживаРҪРёРөРј СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёС… СҖСҸРҙРҫРІ.