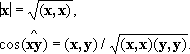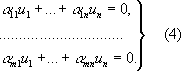|
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ВЕ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ВЕ) - Чтение (стр. 8)
Вектор-функции скалярных аргументов.В механике, физике, дифференциальной геометрии широко используется понятие вектор-функции одного или нескольких скалярных аргументов. Если каждому значению переменной tиз некоторого множества н tэ ставится в соответствие по известному закону определённый вектор r, то говорят, что на множестве н tэ задана вектор-функция (векторная функция) r = r ( t) .Так как вектор r определяется координатами н x, y, zэ, то задание вектор-функции r = r ( t) эквивалентно заданию трёх скалярных функций: х= x( t) , y= y( t) , z= z( t). Понятие вектор-функции становится особенно наглядным, если обратиться к так называемому годографу этой функции, то есть к геометрическому месту концов всех векторов r ( t ) ,приложенных к началу координат О ( рис. 7 ). Если при этом рассматривать аргумент tкак время, то вектор-функция r ( t) представляет собой закон движения точки М,движущейся по кривой L -годографу функции r ( t) . Для изучения вектор-функций важную роль играет понятие производной. Это понятие вводится следующим образом: аргументу
tпридаётся приращение
Dt ¹ 0и вектор
D
r=
r
(
t+
Dt)
-
r(
t) (
на рис. 7
это вектор
( r 1, r 2) '= ( r' 1, r 2) + ( r 1, r' 2) , [ r 1, r 2] ’= [ r' 1, r 2] + [ r 1, r' 2] . В дифференциальной геометрии вектор-функции одного аргумента используются для задания кривых. Для задания поверхностей пользуются вектор-функциями двух аргументов. Векторный анализ.В механике, физике и геометрии широко используются понятия скалярного и векторного поля. Температура неравномерно нагретой пластинки, плотность неоднородного тела представляют собой физические примеры соответственно плоского и пространственного скалярного поля. Векторное поле образует множество всех векторов скоростей частиц установившегося потока жидкости. Примерами векторных полей могут служить также поле силы тяжести, магнитное и электрическое напряжение электромагнитного поля. Для математического задания скалярных и векторных полей используются соответственно скалярные и векторные функции. Ясно, что плотность тела представляет собой скалярную функцию точки, а поле скоростей частиц установившегося потока жидкости - векторную функцию точки. Математический аппарат теории поля обычно называют векторным анализом. Для геометрической характеристики скалярного поля используются понятия линий и поверхностей уровня. Линией уровня плоского скалярного поля называется линия, на которой функция, задающая поле, имеет постоянное значение. Аналогично определяется поверхность уровня пространственного поля. Примерами линии уровня могут служить изотермы - линии уровня скалярного поля температур неравномерно нагретой пластинки. Обратимся к поверхности (линии) уровня скалярного поля, проходящей через данную точку М.При смещении по нормали к этой поверхности (линии) в точке Мнаблюдается максимальное изменение в этой точке функции fзадающей поле. Это изменение характеризуется с помощью градиента скалярного поля. Градиент представляет собой вектор, направленный по нормали к поверхности (линии) уровня в точке Мв сторону возрастания fэтой точке. Величина градиента равна производной fуказанном направлении. Обозначается градиент символом grad f. В базисе i, j k градиент grad fимеет координаты
для плоского поля координаты градиента равны
Градиент скалярного поля представляет собой векторное поле. Для характеристики векторных полей вводится целый ряд понятий: векторной линии, векторной трубки, циркуляции векторного поля, дивергенции и вихря (ротора) векторного поля. Пусть в некоторой области Wзадано векторное поле посредством векторной функции а ( М) переменной точки Миз W. Линия Lв области Wназывается векторной линией, если вектор касательной в каждой её точке Мнаправлен по вектору а ( М) ( рис. 8 ). Если поле а ( М) - поле скоростей частиц стационарного потока жидкости, то векторные линии этого поля - траектории частиц жидкости. Часть пространства в W, состоящая из векторных линий, называется векторной трубкой ( рис. 9 ). Если обратиться к векторному полю скоростей частиц стационарного потока жидкости, то векторная трубка есть часть пространства, которую «заметает» при своём перемещении некоторый фиксированный объём жидкости. Пусть АВ -некоторая гладкая линия в W, l- длина дуги АВ,отсчитываемая от точки Адо переменной точки Мэтой линии, t -единичный вектор касательной к АВв М.Циркуляцией поля а ( М) вдоль кривой АВназывается выражение
Если b ( M) -силовое поле, то циркуляция авдоль АВпредставляет собой работу этого поля вдоль пути АВ. Дивергенция векторного поля а ( М) ,имеющего в базисе i, j, k координаты Р, Q, R, определяется как сумма
и обозначается символом div а.Например, дивергенция гравитация поля, создаваемого некоторым распределением масс, равна плотности (объёмной) r( х, у, z) этого поля, умноженной на 4p. Вихрь (или ротор) векторного поля а ( М) представляет собой векторную характеристику «вращательной составляющей» этого поля. Вихрь поля а обозначается rot а .Если Р, Q, R -координаты а в базисе i, j, k,то
Пусть поле a есть поле скоростей потока жидкости. Поместим в данной точке потока малое колесико с лопастями и ориентируем его ось по направлению rot авэтой точке. Тогда скорость потока будет максимальной, а её значение будет равно
Градиент скалярного поля, дивергенция и вихрь векторного поля обычно называют основными дифференциальными операциями векторного анализа. Справедливы следующие формулы, связывающие эти операции: grad( fh) = f grad h+ h grad f, div( f a) = ( a, grad f) + f div a, rot( f a) = f rot a+ [ grad f, a] , div[ a, b] = ( b, rot a) -( a, rot b) . Векторное поле а ( М) называется потенциальным, если это поле представляет собой градиент некоторого скалярного поля f( M) .При этом поле f( M) называется потенциалом векторного поля а.Для того чтобы поле а,координаты которого Р, Q, Rимеют непрерывные частные производные, было потенциальным, необходимо и достаточно обращение в нуль вихря этого поля. Если в односвязной области Wзадано потенциальное поле а ( М), то потенциал f( M) этого поля может быть найден по формуле
в которой AM -любая гладкая кривая, соединяющая фиксированную точку Аиз Wс точкой М, t-единичный вектор касательной кривой AMи l -длина дуги AM,отсчитываемая от точки А. Векторное поле а ( М) называется соленоидальным, или трубчатым, если это поле представляет собой вихрь некоторого поля b ( M) .Поле b ( M) называется векторным потенциалом поля a . Для того чтобы а было соленоидальным, необходимо и достаточно обращение в нуль дивергенции этого поля. В векторном анализе важную роль играют интегральные соотношения: Остроградского формула,именуемая также основной формулой векторного анализа, и Стокса формула.Пусть V -область, граница Гкоторой состоит из конечного числа кусков гладких поверхностей, n - единичный вектор внешней нормали к Г. Пусть в области Vзадано такое векторное поле а ( М) ,что div апредставляет собой непрерывную функцию. Тогда справедливо соотношение
называемое формулой Остроградского. Если a - поле скоростей установившегося потока несжимаемой жидкости, то ( a , n ) ds -объём жидкости, протекающей в единицу времени через площадку dsна границе Г. Поэтому правая часть формулы (1) представляет собой поток жидкости через границу Гтела Vв единицу времени. Так как в рассматриваемом случае div ахарактеризует интенсивность источников жидкости, то формула Остроградского выражает следующий наглядный факт: поток жидкости через замкнутую поверхность Г равен количеству жидкости, порождаемой всеми источниками, расположенными внутри Г. Пусть в области Wзадано непрерывное и дифференцируемое векторное поле а , имеющее непрерывный вихрь rot а. Пусть Г - ориентируемая поверхность, состоящая из конечного числа кусков гладких поверхностей, n-единичный вектор нормали к Г, t - единичный вектор касательной к краю gповерхности Г, l- длина дуги g.Справедливо следующее соотношение
называемое формулой Стокса. Формула (2) выражает следующий физический факт: поток вихря векторного поля а через поверхность Гравен циркуляции этого поля вдоль кривой g.Формула Остроградского служит источником инвариантного (независящего от выбора системы координат) определения основных операций векторного анализа. Например, из этой формулы вытекает, что
Так как выражение
представляет собой поток жидкости через Г, а
величину этого потока на единицу объёма, то определение div ас помощью соотношения (3) показывает, что div ахарактеризует интенсивность источника в данной точке. Лит.:Кочин Н. Е., Векторное исчисление и начала тензорного исчисления, 6 изд., Л.-М., 1938; Дубнов Я. С., Основы векторного исчисления, 4 изд., т. 1-2, М., 1950-52; Будак Б. М., Фомин С. В., Кратные интегралы и ряды, 2 изд., М., 1967. Э. Г. Позняк. 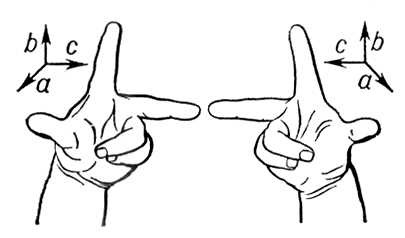
Рис. 6 к ст. Векторное исчисление. 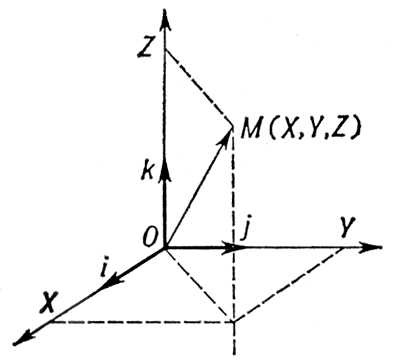
Рис. 5 к ст. Векторное исчисление. 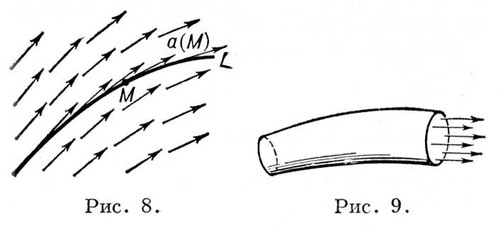
Рисунки 8, 9 к ст. Векторное исчисление. 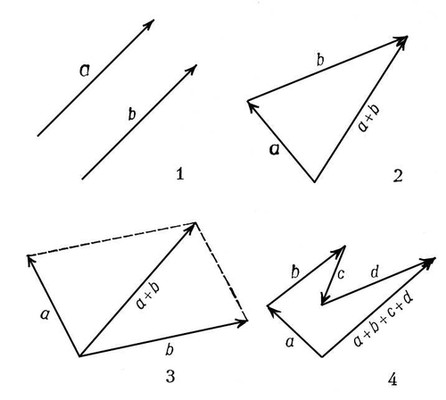
Рисунки 1-4 к ст. Векторное исчисление. 
Рис. 7 к ст. Векторное исчисление. Векторное поле Ве'кторное по'ле, область, в каждой точке Ркоторой задан вектор а( Р). Математически В. п. может быть определено в данной области Gпосредством вектор-функции a( Р) переменной точки Рэтой области. К понятию В. п. приводит целый ряд физических явлений и процессов (например, векторы скоростей частиц движущейся жидкости в каждый момент времени образуют В. п.). Теория В. п. широко разработана и имеет разнообразные применения в различных областях естествознания (см. Векторное исчисление ) .
Лит.:Будак Б. М.. Фомин С. В., Кратные интегралы и ряды, 2 изд., М., 1967. Э. Г. Позняк. Векторное произведение
Ве'кторное произведе'ниевектора
а
на вектор
b
- вектор, обозначаемый [
а, b
] и определяемый так: 1) длина вектора [
а, b
] равна произведению длин векторов
а
и
b
на синус угла
jмежду ними (берётся тот из двух углов между
а
и
b
, который не превосходит
p), 2) вектор [
а, b
]
перпендикулярен вектору
а
и вектору
b
, 3) тройка векторов
а,
b, [
а, b
], согласно с ориентацией пространства, всегда правая или всегда левая (см.
Векторное исчисление
)
.В. п. широко применяется в геометрии, механике и физике (например, момент силы
F,приложенной к точке
Мотносительно точки
О, есть В. п. [
Лит.;Ильин В. А., Позняк Э. Г., Аналитическая геометрия, М., 1968. Э. Г. Позняк. Векторное пространство Ве'кторное простра'нство,математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трёхмерного пространства. Определение В. п.Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа (см. Векторное исчисление ) .В применении к любым векторам х, у, zи любым числам a, bэти правила удовлетворяют следующим условиям (условия А): 1) х+ у= у+ х(перестановочность сложения); 2) ( х+ у) + z= x+ ( y+ z) (ассоциативность сложения); 3) имеется нулевой вектор 0(или нуль-вектор), удовлетворяющий условию x+ 0= x:для любого вектора x ; 4) для любого вектора хсуществует противоположный ему вектор утакой, что х+ у= 0, 5) 1 · х= х, 6) a( bx) = ( ab) х(ассоциативность умножения); 7) ( a+ b) х= aх+ bх(распределительное свойство относительно числового множителя); 8) a( х+ у) = aх+ aу (распределительное свойство относительно векторного множителя). Векторным (или линейным) пространством называется множество R,состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям А(условия 1-3 выражают, что операция сложения, определённая в В. п., превращает его в коммутативную группу). Выражение a 1e 1+ a 2e 2+ …+ a ne n (1) называется линейной комбинацией векторов e 1, e 2,..., e nс коэффициентами a 1, a 2, ..., a n.Линейная комбинация (1) называется нетривиальной, если хотя бы один из коэффициентов a 1, a 2,..., a nотличен от нуля. Векторы e 1, e 2,..., e nназываются линейно зависимыми, если существует нетривиальная комбинация (1), представляющая собой нулевой вектор. В противном случае (то есть если только тривиальная комбинация векторов e 1, e 2,..., e nравна нулевому вектору) векторы e 1, e 2,..., e nназывается линейно независимыми. Векторы (свободные) трёхмерного пространства удовлетворяют следующему условию (условие В): существуют три линейно независимых вектора; любые четыре вектора линейно зависимы (любые три ненулевых вектора, не лежащие в одной плоскости, являются линейно независимыми). В. п. называется n-мepным (или имеет «размерность n») ,если в нём существуют nлинейно независимых элементов e 1, e 2,..., e n,а любые n+ 1элементов линейно зависимы (обобщённое условие В). В. п. называются бесконечномерным, если в нём для любого натурального nсуществует nлинейно независимых векторов. Любые nлинейно независимых векторов n-мepного В. п. образуют базис этого пространства. Если e 1, e 2,..., e n- базис В. п., то любой вектор х этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов: x= a 1e 1+ a 2e 2+ ...+ a ne n. При этом числа a 1, a 2,..., a nназываются координатами вектора хв данном базисе. Примеры В. п.Множество всех векторов трёхмерного пространства образует, очевидно, В. п. Более сложным примером может служить так называемое n-мерное арифметическое пространство. Векторами этого пространства являются упорядоченные системы из nдействительных чисел : l 1, l 2,..., l n.Сумма двух векторов и произведение на число определяются соотношениями: ( l 1, l 2, …, l n) + ( m 1, m 2, …, m n) = ( l 1+ m 1, l 2+ m 2, …, l n+ m n) ; a( l 1, l 2, …, l n) = ( al 1, al 2, …, al n) . Базисом в этом пространстве может служить, например, следующая система из nвекторов e 1= (1, 0,..., 0), e 2= (0, 1,..., 0),..., e n= (0, 0,..., 1). Множество Rвсех многочленов a 0+ a 1u+ …+ a nu n(любых степеней n) от одного переменного с действительными коэффициентами a 0, a 1,..., a nс обычными алгебраическими правилами сложения многочленов и умножения многочленов на действительные числа образует В. п. Многочлены 1, u, u 2,..., u n(при любом n) линейно независимы в R,поэтому R -бесконечномерное В. п. Многочлены степени не выше nобразуют В. п. размерности n+ 1; его базисом могут служить многочлены 1, u, u 2,..., u n. Подпространства В. п.В .п. R'называется подпространством R,если R' Н R(то есть каждый вектор пространства R'есть и вектор пространства R) и если для каждого вектора v О r'и для каждых двух векторов v 1и v 2( v 1, v 2О R') вектор lv(при любом l) и вектор v 1+ v 2один и тот же независимо от того, рассматриваются ли векторы v, v 1, v 2как элементы пространства R'или R.Линейной оболочкой векторов x 1, x 2,... x pназывается множество всевозможных линейных комбинаций этих векторов, то есть векторов вида a 1x 1+ a 2x 2+ …+ a px p. В трёхмерном пространстве линейной оболочкой одного ненулевого вектора x 1будет, очевидно, совокупность всех векторов, лежащих на прямой, определяемой вектором x 1.Линейной оболочкой двух не лежащих на одной прямой векторов x 1и x 2будет совокупность всех векторов, расположенных в плоскости, которую определяют векторы x 1и x 2.В общем случае произвольного В. п. Rлинейная оболочка векторов x 1, x 2,..., x pэтого пространства представляет собой подпространство пространства Rразмерности р.В n-мерном В. п. существуют подпространства всех размерностей, меньших р.Всякое конечномерное (данной размерности k) подпространство R'В. п. Rесть линейная оболочка любых kлинейно независимых векторов, лежащих в R'.Пространство, состоящее из всех многочленов степени Ј n(линейная оболочка многочленов 1, u, u 2,..., u n) ,есть ( n+ 1) -мepное подпространство пространства Rвсех многочленов. Евклидовы пространства.Для развития геометрических методов в теории В. п. нужно указать пути обобщения таких понятий, как длина вектора, угол между векторами и т.п. Один из возможных путей заключается в том, что любым двум векторам хи уиз Rставится в соответствие число, обозначаемое ( х, у) и называемое скалярным произведением векторов хи у.При этом требуется, чтобы выполнялись следующие аксиомы скалярного произведения: 1) ( х, у) = ( у, х) (перестановочность); 2) ( x 1+ x 2, y) = ( x 1, y) + ( x 2, y) (распределительное свойство); 3) ( ax, у) = a( х, у) , 4) ( х, х) ³ 0для любого х, причем ( х, х) = 0 только для х= 0. Обычное скалярное произведение в трёхмерном пространстве этим аксиомам удовлетворяет. В. п., в котором определено скалярное произведение, удовлетворяющее перечисленным аксиомам, называется евклидовым пространством; оно может быть как конечномерным (n-мерным), так и бесконечномерным. Бесконечномерное евклидово пространство обычно называют
гильбертовым пространством.Длина |
x| вектора
xи угол
Примером евклидова пространства может служить обычное трёхмерное пространство со скалярным произведением, определяемым в векторном исчислении. Евклидово n-мepное (арифметическое) пространство E nполучим, определяя в n-мepном арифметическом В. п. скалярное произведение векторов x= ( l 1, …, l n) и y= ( m 1, …, m n) соотношением ( x, y) = l 1m 1+ l 2m 2+ …+ l nm n. (2) При этом требования 1)-4), очевидно, выполняются. В евклидовых пространствах вводится понятие ортогональных (перпендикулярных) векторов. Именно векторы хи уназываются ортогональными, если их скалярное произведение равно нулю: ( х, у) = 0.В рассмотренном пространстве E nусловие ортогональности векторов x= ( l 1, …, l n) и y= ( m 1, …, m n) ,как это следует из соотношения (2), имеет вид: l 1m 1+ l 2m 2+ …+ l nm n= 0.(3) Применение В. п. Понятие В. п. (и различные обобщения) широко применяется в математике и её приложениях к естествознанию. Пусть, например, R -множество всех решений линейного однородного дифференциального уравнения y n+ a 1( x) y ( n+ 1)+ …+ a n( x) y= 0. Ясно, что сумма двух решений и произведение решения на число являются решениями этого уравнения. Таким образом, Rудовлетворяет условиям А. Доказывается, что для Rвыполнено обобщённое условие В. Следовательно, Rявляется В. п. Любой базис в рассмотренном В. п. называется фундаментальной системой решений, знание которой позволяет найти все решения рассматриваемого уравнения. Понятие евклидова пространства позволяет полностью геометризовать теорию систем однородных линейных уравнений:
Рассмотрим в евклидовом пространстве E nвекторы a i= ( a i1, a i2, …, a in) , i= 1, 2,..., nи вектор-решение u= ( u 1, u 2,..., u n). Пользуясь формулой (2) для скалярного произведения векторов E n,придадим системе (4) следующий вид: ( a i, u) = 0, i= 1, 2, …, m. (5) Из соотношений (5) и формулы (3) следует, что вектор-решение uортогонален всем векторам a i.Иными словами, этот вектор ортогонален линейной оболочке векторов a i,то есть решение uесть любой вектор из ортогонального дополнения линейной оболочки векторов a i. Важную роль в математике и физике играют и бесконечномерные линейные пространства.Примером такого пространства может служить пространство Снепрерывных функций на отрезке с обычной операцией сложения и умножения на действительные числа. Упомянутое выше пространство всех многочленов является подпространством пространства С. Лит.:Александров П. С., Лекции по аналитической геометрии, М., 1968; Гельфанд И, М., Лекции по линейной алгебре, М. - Л., 1948. Э. Г. Позняк. Вектор-потенциал Ве'ктор-потенциа'л,см. Потенциалы электромагнитного поля. Вектор-функция 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76 |
|||||||
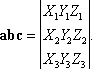
 ) множится на
1/Dt. Предел выражения
D
r/Dtпри
Dt ® 0называется производной вектор-функции
r
(
t) и обозначается
r'(
t) или
d
r/dt. Производная представляет собой вектор, касательный к годографу
Lв данной точке
М.Если вектор-функция рассматривается как закон движения точки по кривой
L,то производная
r'(
t) равна скорости движения этой точки. Правила вычисления производных различных произведений вектор-функций подобны правилам вычисления производных произведений обычных функций. Например,
) множится на
1/Dt. Предел выражения
D
r/Dtпри
Dt ® 0называется производной вектор-функции
r
(
t) и обозначается
r'(
t) или
d
r/dt. Производная представляет собой вектор, касательный к годографу
Lв данной точке
М.Если вектор-функция рассматривается как закон движения точки по кривой
L,то производная
r'(
t) равна скорости движения этой точки. Правила вычисления производных различных произведений вектор-функций подобны правилам вычисления производных произведений обычных функций. Например,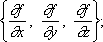
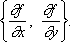
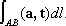
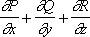
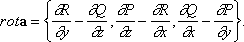
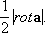
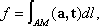
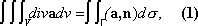
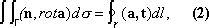
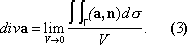
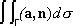
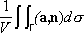
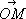 ,
F
]).
,
F
]).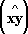 между векторами
хи
уевклидова пространства определяются через скалярное произведение формулами
между векторами
хи
уевклидова пространства определяются через скалярное произведение формулами