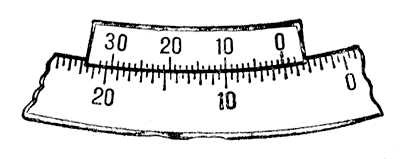
Верньо Пьер Виктюрньен

Верньо'(Vergniaud) Пьер Виктюрньен (31.5.1753, Лимож, - 31.10.1793, Париж), деятель Великой французской революции. Адвокат. В 1791 избран депутатом Законодательного собрания; был его председателем во время восстания 10 августа 1792, свергнувшего монархию. Один из лидеров жирондистов,В. был избран депутатом Конвента, где выступал решительным противником монтаньяров. После победы народного восстания 31 мая - 2 июня 1793 был арестован и по приговору Революционного трибунала казнён.

Верона

Веро'на(Verona), город на С.-В. Италии, в области Венеция, у подножия Альп, по обоим берегам р. Адидже. Административный центр провинции Верона. 254,9 тыс. жителей (1969). Важный транспортный узел на путях из Венеции в Милан и из Паданской равнины в Австрию (через перевал Бреннер). Машиностроительная, химическая, полиграфическая, текстильная, деревообрабатывающая, бумажная, пищевая промышленность. Периодические международные с.-х. ярмарки. Индустриальный институт.

  В. - древнее поселение, с 89 до н. э. - римская колония. Близ В. в 489 король остготов Теодорих одержал победу над Одоакром и сделал её одной из своих резиденций. При лангобардах (568-774) В. - центр одного из дукатов (герцогств). С начала 12 в. - городская коммуна. В 12 в. В. входила в Ломбардскую лигу.В В. раньше, чем в большинстве городов Италии, сложилась тирания. В 1387 В. была присоединена к Милану, в 1405 - к Венеции, вместе с которой по Кампоформийскому миру 1797 отошла к Австрии. В 1866 вошла в состав Итальянского королевства.

  Сохранились римские арена, театр, остатки укреплений (Порта деи Борсари, Порта деи Леони), восходящий к античности мост Поите Пьетра. Облик старой части В. с её узкими прямыми улицами определяют многочисленными средневековыми постройки. В центре В. - 2 площади: Пьяцца делле Эрбе (бывший античный форум) с готическими домами Каса деи Мерканти (1301) и Торре дель Гарделло (1370) и барочным Палаццо Маффеи (1668); Пьяцца деи Синьори с романским Палаццо дель Комуне (начато в 1193), дворцом Скалигеров (Палаццо дель Говерно; конец 13 в.) и ренессансной Лоджией дель Консильо (1475-92, архитектор Фра Джоконде). Романские церковь Сан-Дзено Маджоре (5 в., перестроена в 9 в. и 1120-38; бронзовые двери портала - 11-12 вв.) и собор (1139-87; кампанила - 16 в., архитектор М. Санмикели); готическая церковь Сант-Анастазия (1291-1323 и 1422-81, в интерьере - фрески Пизанелло). Готический замок Кастельвеккьо (1354-75) с мостом Скалигеров и предмостными башнями. Ренессансные дворцы (Помпеи, 1530: Каносса, около 1530; Бевилаква, 1532) и ворота городских укреплений (Порта Нуова, 1533-40; Порта Палио, 1557; и др.) все архитектор М. Санмикели. Музеи: Археологический музей, Музей Кастельвеккьо, Галерея современного искусства.

  Лит.:Simeoni L.. Verona, Roma, 1929; Schmid Е., Verona. Brescia, Frauenfeld, 1961.

Верона. Церковь Сан-Дзено Маджоре (1120-38).

Веронал

Верона'л,лекарственный препарат, то же, что барбитал.См. Снотворные средства.

Веронезе Паоло

Вероне'зе(Veronese; собственно Кальяри, Caliari) Паоло (1528, Верона, - 19.4.1588, Венеция), венецианский живописец Позднего Возрождения. Учился у веронского художника А. Бадиле. Работал, главным образом, в Венеции (с 1553), а также в Вероне, Мантуе, Виченце и Падуе. В 1560, возможно, посетил Рим. Произведения В. конца 1540 - начала 1550-х гг. говорят об изучении им рисунка Микеланджело,композиционных построений Рафаэля и Корреджо,колористических открытий Тициана.К середине 1550-х гг. складывается самостоятельный стиль В., сочетающий лёгкий, артистически изощренный рисунок и пластику форм с изысканной колористической гаммой, основанной на сложных созвучиях чистых цветов, объединённых светоносным серебристым тоном. Главная сфера деятельности В. - монументально-декоративная живопись. Его исполненные маслом на холсте крупные многофигурные композиции, украшающие стены и плафоны светских и культовых зданий Венеции, часто служат прославлению величия и военных триумфов Венецианской республики. Им присущи героическая приподнятость образов, энергичная светотеневая лепка, выразительность ракурсов и движений, праздничное, ликующее великолепие цвета («Старость и Юность», 1553, «Диалектика», 1575-77, «Триумф Венеции», 1578-1585, - все во Дворце дожей, Венеция; «Триумф Мардохея» и др., 1556, церковь Сан-Себастьяно, Венеция). Выполненные В. фрески в загородных венецианских виллах (вилле Соранцо, 1551, фрагменты фресок ныне в соборе в Кастель-Франко; вилле Барбаро-Вольпи в Мазере близ Тревизо, около 1561), с их холодной воздушной цветовой гаммой, отличаются большей интимностью образов; наряду с мифологическими композициями и аллегорическими фигурами в них встречаются пейзажи и жанровые сцены с шутливыми иллюзионистическими эффектами. Воплощая гуманистическое идейно-образное содержание в целостных, законченных монументально-декоративных формах, органически связывая живопись с архитектурой, В. развивает на новом этапе лучшие достижения искусства эпохи Возрождения. Излюбленный вид станковой картины В. - торжественные многофигурные композиции с изображением праздничных пиршеств, шествий и аудиенций, в которых человек выступает во взаимосвязи с окружающей его общественной средой («Брак в Кане», 1563, Лувр, Париж; «Семья Дария у ног Александра», после 1565, Национальная галерея, Лондон; цикл картин для семьи Куччина, в том числе «Брак в Кане» и «Поклонение волхвов», около 1571, - обе в Картинной галерее, Дрезден; «Пир в доме Левия», 1573, Галерея Академии, Венеция). Смелое введение конкретных жизненных наблюдений, жанровых мотивов, портретов современников стало причиной обвинения В. инквизицией в 1573 в излишне светской трактовке религиозных тем. В. создал большое число алтарных образов, разнообразных по замыслу и композиционным решениям («Мадонна с младенцем и святыми», около 1562, «Обручение св. Екатерины», около 1575, - оба в Галерее Академии, Венеция). Немногочисленным портретам В. свойственны мягкая лиричность, иногда оттенок жанровости («Белла Нани», 1550-е гг., Лувр, Париж; «Граф да Порто с сыном Адриано», около 1556, собрание Контини-Бонакосси, Флоренция). Последние годы творчества В. отмечены признаками кризиса ренессансного мировоззрения. В работах В. 1580-х гг. появляются холодная парадность и внешняя патетика; в них проскальзывают вместе с тем настроения смутной тревоги, скорби и меланхолии («Похищение Европы», 1580, Дворец дожей, Венеция; «Агарь и Исмаил в пустыне», 1580-е гг., Художественно-исторический музей, Вена; «Оплакивание Христа», начало 1580-х гг., Эрмитаж, Ленинград). Рафинированный, богатый тончайшими переливами красок колорит становится менее звучным. Среди учеников В. - его брат Бенедетто, сыновья Карло и Габриеле.

  Лит.:Антонова И. А., Веронезе, М., 1957; Fiocco G., Paolo Veronese, Bologna,, 1928; Palucchini R., Catalogo della mostra di Paolo Veronese, Venezia, 1939; его же, Veronese, 3 ed., Bergamo, 1953.

  И. А. Антонова.

Паоло Веронезе. Автопортрет. Деталь картины «Пир в доме Левия» (1573, Галерея Академии, Венеция).

Вероника

Верони'ка(Veronica), род растений семейства норичниковых. Одно -, дву- или многолетние травы, иногда полукустарнички. Венчик голубой, синий, белый или иной окраски, обычно 4-лопастный, часто колосовидный; тычинок - 2; плод - двух-гнёздная коробочка. Около 300 видов, обитающих, главным образом, в умеренных и холодных областях Северного полушария, часто на высокогорьях. В СССР свыше 140 видов, встречающихся повсеместно. Некоторые В. разводят как декоративные. К роду В. часто присоединяют виды рода геба (Hebe) - более 100 видов кустарников и невысоких деревьев, растущих, главным образом, в Н. Зеландии (около 90 эндемичных представителей), а также в Австралии, Тасмании, Новой Гвинее и умеренных областях Южной Америки. Вечнозелёные красиво цветущие виды геба часто культивируют; в СССР - на Кавказе и в Крыму.

  М. Э. Кирпичников.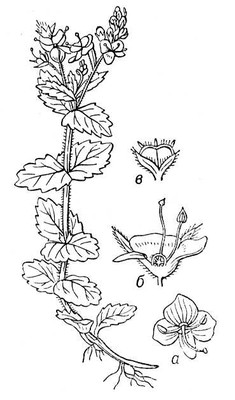

Вероника дубравная: а - цветок, б - цветок в разрезе, в - плод.

Веронский конгресс 1822

Веро'нский конгре'сс 1822,см. в ст. Священный союз.

Вероятное отклонение

Вероя'тное отклоне'ние,одна из мер рассеяния случайных величин.Если аесть математическое ожидание случайной величины Хи распределение вероятностей этой величины непрерывно, то В. о. Е _хопределяется требованием, чтобы вероятность отклонений Хот а,больших по абсолютной величине, чем Е _х,равнялась вероятности отклонений меньших по абсолютной величине, чем E _x.Если величина Химеет нормальное распределение с дисперсией s ² ,то E _x= 0,6745s или, округляя этот результат, величина срединного (вероятного) отклонения (ошибки) равна величины среднего квадратичного отклонения (ошибки).

Вероятностей теория

Вероя'тностей тео'рия,математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким-либо образом с первыми.

  Утверждение о том, что какое-либо событие наступает с вероятностью,равной, например, , ещё не представляет само по себе окончательной ценности, так как мы стремимся к достоверному знанию. Окончательную познавательную ценность имеют те результаты В. т., которые позволяют утверждать, что вероятность наступления какого-либо события Авесьма близка к единице или (что то же самое) вероятность не наступления события Авесьма мала. В соответствии с принципом «пренебрежения достаточно малыми вероятностями» такое событие справедливо считают практически достоверным. Ниже (в разделе Предельные теоремы) показано, что имеющие научный и практический интерес выводы такого рода обычно основаны на допущении, что наступление или не наступление события Азависит от большого числа случайных, мало связанных друг с другом факторов (см. по этому поводу Больших чисел закон ) .Поэтому можно также сказать, что В. т. есть математическая наука, выясняющая закономерности, которые возникают при взаимодействии большого числа случайных факторов.

  Предмет теории вероятностей.Для описания закономерной связи между некоторыми условиями Sи событием А,наступление или не наступление которого при данных условиях может быть точно установлено, естествознание использует обычно одну из следующих двух схем:

  а) при каждом осуществлении условий Sнаступает событие А.Такой вид, например, имеют все законы классической механики, которые утверждают, что при заданных начальных условиях и силах, действующих на тело или систему тел, движение будет происходить однозначно определённым образом.

  б) При условиях Sсобытие Аимеет определённую вероятность P( A / S) ,равную р.Так, например, законы радиоактивного излучения утверждают, что для каждого радиоактивного вещества существует определённая вероятность того, что из данного количества вещества за данный промежуток времени распадётся какое-либо число Nатомов.

  Назовем частотой события Ав данной серии из nиспытаний (то есть из nповторных осуществлений условий S) отношение h = m/nчисла mтех испытаний, в которых Анаступило, к общему их числу n.Наличие у события Апри условиях Sопределённой вероятности, равной р,проявляется в том, что почти в каждой достаточно длинной серии испытаний частота события Априблизительно равна р.

 Статистические закономерности, то есть закономерности, описываемые схемой типа (б), были впервые обнаружены на примере азартных игр, подобных игре в кости. Очень давно известны также статистические закономерности рождения, смерти (например, вероятность новорождённому быть мальчиком равна 0,515). Конец 19 в. и 1-я половина 20 в. отмечены открытием большого числа статистических закономерностей в физике, химии, биологии и т.п.

  Возможность применения методов В. т. к изучению статистических закономерностей, относящихся к весьма далёким друг от друга областям науки, основана на том, что вероятности событий всегда удовлетворяют некоторым простым соотношениям, о которых будет сказано ниже (см. раздел Основные понятия теории вероятностей). Изучение свойств вероятностей событий на основе этих простых соотношений и составляет предмет В. т.

  Основные понятия теории вероятностей.Наиболее просто определяются основные понятия В. т. как математической дисциплины в рамках так называемой элементарной В. т. Каждое испытание Т,рассматриваемое в элементарной В. т., таково, что оно заканчивается одним и только одним из событий E ₁ , E ₂ ,..., E _S(тем или иным, в зависимости от случая). Эти события называются исходами испытания. С каждым исходом E _kсвязывается положительное число р _к-вероятность этого исхода. Числа p _kдолжны при этом в сумме давать единицу. Рассматриваются затем события А,заключающиеся в том, что «наступает или E _i,или E _j,...,или E _k». Исходы E _i, E _j,..., E _kназываются благоприятствующими А,и по определению полагают вероятность Р( А) события А, равной сумме вероятностей благоприятствующих ему исходов:

  P( A) = p _i+ p _s+ …+ p _k.     (1)

  Частный случай p ₁= p ₂=... p _s= 1/Sприводит к формуле

  Р( А) = r/s.     (2)

  Формула (2) выражает так называемое классическое определение вероятности, в соответствии с которым вероятность какого-либо события Аравна отношению числа rисходов, благоприятствующих А,к числу sвсех «равновозможных» исходов. Классическое определение вероятности лишь сводит понятие «вероятности» к понятию «равновозможности», которое остаётся без ясного определения.

  Пример. При бросании двух игральных костей каждый из 36 возможных исходов может быть обозначен ( i, j) ,где i- число очков, выпадающее на первой кости, j -на второй. Исходы предполагаются равновероятными. Событию А -«сумма очков равна 4», благоприятствуют три исхода (1; 3), (2; 2), (3; 1). Следовательно, Р( A) = 3/36 =1/12.

  Исходя из каких-либо данных событий, можно определить два новых события: их объединение (сумму) и совмещение (произведение). Событие Вназывается объединением событий A ₁, A ₂,..., A _r,-,если оно имеет вид: «наступает или A ₁,или А ₂,...,или A _r».

  Событие С называется совмещением событий A ₁, А. ₂,..., A _r,если оно имеет вид: «наступает и A ₁, и A ₂,...,и A _r» .Объединение событий обозначают знаком И, а совмещение - знаком З. Таким образом, пишут:

  B = A ₁И A ₂И … И A _r, C= A ₁З A ₂З … З A _r.

  События Аи Вназывают несовместными, если их одновременное осуществление невозможно, то есть если не существует среди исходов испытания ни одного благоприятствующего и А,и В.

 С введёнными операциями объединения и совмещения событий связаны две основные теоремы В. т. - теоремы сложения и умножения вероятностей.

  Теорема сложения вероятностей. Если события A ₁, A ₂,..., A _rтаковы, что каждые два из них несовместны, то вероятность их объединения равна сумме их вероятностей.

  Так, в приведённом выше примере с бросанием двух костей событие В -«сумма очков не превосходит 4», есть объединение трёх несовместных событий A ₂, A ₃, A ₄, заключающихся в том, что сумма очков равна соответственно 2, 3, 4. Вероятности этих событий 1/36; 2/36; 3/36. По теореме сложения вероятность Р( В) равна

  1/36 + 2/36 + 3/36 = 6/36 = 1/6.

  Условную вероятность события Впри условии Аопределяют формулой

  что, как можно показать, находится в полном соответствии со свойствами частот. События A ₁, A ₂,..., A _rназываются независимыми, если условная вероятность каждого из них при условии, что какие-либо из остальных наступили, равна его «безусловной» вероятности (см. также Независимость в теории вероятностей).

  Теорема умножения вероятностей. Вероятность совмещения событий A ₁, A ₂,..., A _rравна вероятности события A ₁, умноженной на вероятность события A ₂, взятую при условии, что А ₁наступило,..., умноженной на вероятность события A _rпри условии, что A ₁, A ₂,..., A _r-1наступили. Для независимых событий теорема умножения приводит к формуле:

  P( A ₁З A ₂З … З A _r) = P( A ₁) · P( A ₂) · … · P( A _r) ,    (3)

  то есть вероятность совмещения независимых событий равна произведению вероятностей этих событий. Формула (3) остаётся справедливой, если в обеих её частях некоторые из событий заменить на противоположные им.

  Пример. Производится 4 выстрела по цели с вероятностью попадания 0,2 при отдельном выстреле. Попадания в цель при различных выстрелах предполагаются независимыми событиями. Какова вероятность попадания в цель ровно три раза?

  Каждый исход испытания может быть обозначен последовательностью из четырёх букв [напр., (у, н, н, у) означает, что при первом и четвёртом выстрелах были попадания (успех), а при втором и третьем попаданий не было (неудача)]. Всего будет 2·2·2·2 = 16 исходов. В соответствии с предположением о независимости результатов отдельных выстрелов следует для определения вероятностей этих исходов использовать формулу (3) и примечание к ней. Так, вероятность исхода (у, н. н, н) следует положить равной 0,2·0,8·0,8·0,8 = 0,1024; здесь 0,8 = 1-0,2 - вероятность промаха при отдельном выстреле. Событию «в цель попадают три раза» благоприятствуют исходы (у, у, у, н), (у, у, н, у), (у, н, у, у). (н, у, у, у), вероятность каждого одна и та же:

  0,2·0,2·0,2·0,8 =...... =0,8·0,2·0,2·0,2 = 0,0064;

  следовательно, искомая вероятность равна

  4·0,0064 = 0,0256.

  Обобщая рассуждения разобранного примера, можно вывести одну из основных формул В. т.: если события A ₁, A ₂,..., A _nнезависимы и имеют каждое вероятность р,то вероятность наступления ровно mиз них равна

  P _n( m) = C _n ^mp ^m( 1 - p) ^n-m;     (4)

  здесь C _n ^mобозначает число сочетаний из nэлементов по m(см. Биномиальное распределение ) .При больших nвычисления по формуле (4) становятся затруднительными. Пусть в предыдущем примере число выстрелов равно 100, и ставится вопрос об отыскании вероятности хтого, что число попаданий лежит в пределах от 8 до 32. Применение формулы (4) и теоремы сложения даёт точное, но практически мало пригодное выражение искомой вероятности

  Приближённое значение вероятности хможно найти по теореме Лапласа (см. Лапласа теорема )

  причём ошибка не превосходит 0,0009. Найденный результат показывает, что событие 8 Ј mЈ 32 практически достоверно. Это самый простой, но типичный пример использования предельных теорем В. т.

  К числу основных формул элементарной В. т. относится также так называемая формула полной вероятности: если события A ₁, A ₂,..., A _r попарно несовместны и их объединение есть достоверное событие, то для любого события Вего вероятность равна сумме

  Теорема умножения вероятностей оказывается особенно полезной при рассмотрении составных испытаний. Говорят, что испытание Тсоставлено из испытаний T ₁, T ₂,..., T _n-1, T _n, если каждый исход испытания Тесть совмещение некоторых исходов A _i, B _j,..., X _k, Y _lсоответствующих испытаний T ₁, T ₂,..., T _n-1, T _n. Из тех или иных соображений часто бывают известны вероятности

  P( A _i) , P( B _j/A _i) ,…, P( Y _l/A _iЗ B _jЗ … З X _k). (5)

  По вероятностям (5) с помощью теоремы умножения могут быть определены вероятности Р( Е) для всех исходов Есоставного испытания, а вместе с тем и вероятности всех событий, связанных с этим испытанием (подобно тому, как это было сделано в разобранном выше примере). Наиболее значительными с практической точки зрения представляются два типа составных испытаний: а) составляющие испытания не зависимы, то есть вероятности (5) равны безусловным вероятностям P( A _i) , P( B _j) ,..., P( Y _l) ;б) на вероятности исходов какого-либо испытания влияют результаты лишь непосредственно предшествующего испытания, то есть вероятности (5) равны соответственно: P( A _i) , P( B _j/A _i) ,..., P( Y _i/ X _k) .В этом случае говорят об испытаниях, связанных в цепь Маркова. Вероятности всех событий, связанных с составным испытанием, вполне определяются здесь начальными вероятностями Р( А _i) и переходными вероятностями P( B _j/ A _i) ,..., P( Y _l/ X _k) (см. также Марковский процесс ) .

 Случайные величины. Если каждому исходу E _rиспытания Тпоставлено в соответствие число х,,то говорят, что задана случайная величина X. Среди чисел x ₁, х ₂,......, x _sмогут быть и равные; совокупность различных значений х _гпри r =1, 2,..., sназывают совокупностью возможных значений случайной величины. Набор возможных значений случайной величины и соответствующих им вероятностей называется распределением вероятностей случайной величины (см. Распределения ) .Так, в примере с бросанием двух костей с каждым исходом испытания ( i, j) связывается случайная величина Х = i + j- сумма очков на обеих костях. Возможные значения суть 2, 3, 4,..., 11, 12; соответствующие вероятности равны 1/36, 2/36, 3/36,..., 2/36, 1/36.

  При одновременном изучении нескольких случайных величин вводится понятие их совместного распределения, которое задаётся указанием возможных значений каждой из них и вероятностей совмещения событий

  {X ₁= x ₁}, {X ₂= x ₂}, …, {X _n= x _n},     (6)

  где x _k-какое-либо из возможных значений величины X _k.Случайные величины называются независимыми, если при любом выборе x _kсобытия (6) независимы. С помощью совместного распределения случайных величин можно вычислить вероятность любого события, определяемого этими величинами, например события a < X ₁+ Х ₂+... + X _n< bи т.п.

  Часто вместо полного задания распределения вероятностей случайной величины предпочитают пользоваться небольшим количеством числовых характеристик. Из них наиболее употребительны математическое ожидание и дисперсия.

 В число основных характеристик совместного распределения нескольких случайных величин, наряду с математическими ожиданиями и дисперсиями этих величин, включаются коэффициенты корреляции и т.п. Смысл перечисленных характеристик в значительной степени разъясняется предельными теоремами (см. раздел Предельные теоремы).

  Схема испытаний с конечным числом исходов недостаточна уже для самых простых применений В. т. Так, при изучении случайного разброса точек попаданий снарядов вокруг центра цели, при изучении случайных ошибок, возникающих при измерении какой-либо величины, и т.д. уже невозможно ограничиться испытаниями с конечным числом исходов. При этом в одних случаях результат испытания может быть выражен числом или системой чисел, в других - результатом испытания может быть функция (например, запись изменения давления в данной точке атмосферы за данный промежуток времени), системы функций и т.п. Следует отметить, что многие данные выше определения и теоремы с незначительными по существу изменениями приложимы и в этих более общих обстоятельствах, хотя способы задания распределений вероятностей изменяются (см. Распределения, Плотность вероятности) .

 Наиболее серьёзное изменение претерпевает определение вероятности, которое в элементарном случае давалось формулой (2). В более общих схемах, о которых идёт речь, события являются объединениями бесконечного числа исходов (или, как говорят, элементарных событий), вероятность каждого из которых может быть равна нулю. В соответствии с этим свойство, выраженное теоремой сложения, не выводится из определения вероятности, а включается в него.

  Наиболее распространённая в настоящее время логическая схема построения основ В. т. разработана в 1933 советским математиком А. Н. Колмогоровым. Основные черты этой схемы следующие. При изучении какой-либо реальной задачи - методами В. т. прежде всего выделяется множество Uэлементов u,называемых элементарными событиями. Всякое событие вполне описывается множеством благоприятствующих ему элементарных событий и потому рассматривается как некое множество элементарных событий. С некоторыми из событий Асвязываются определённые числа Р( A), называемые их вероятностями и удовлетворяющие условиям

  1. 0 Ј Р( А) Ј 1,

  2. P( U) = 1,

  3. Если события A ₁,..., A _nпопарно несовместны и А- их сумма, то

  Р( А) = Р( A ₁) + P( A ₂) + … + Р( A _n) .

  Для создания полноценной математической теории требуют, чтобы условие 3 выполнялось и для бесконечных последовательностей попарно несовместных событий. Свойства неотрицательности и аддитивности есть основные свойства меры множества. В. т. может, таким образом, с формальной точки зрения рассматриваться как часть меры теории.Основные понятия В. т. получают при таком подходе новое освещение. Случайные величины превращаются в измеримые функции, их математические ожидания - в абстрактные интегралы Лебега и т.п. Однако основные проблемы В. т. и теории меры различны. Основным, специфическим для В. т. является понятие независимости событий, испытаний, случайных величин. Наряду с этим В. т. тщательно изучает и такие объекты, как условные распределения, условные математические ожидания и т.п.