 |
|
���������� ������:: ��� :: ������� ��� ���������� :: �������� ����� :: ������ ����� :: ����� ����� �������� :: ���� ��������� :: ������ ����� ���� :: ������� ������ :: ������� ������ ���������� :: ������� ���� ���������� �����:: �������� ������ :: ������ � ������ ��� ����� (��������� ��. ����������� � �������� ������ ������) :: �������� ���� :: � ����� ������ �. �������� :: ����� ���� (��� 1) :: ���� (����� 2) :: ������� ����� :: ������ � �� ����� :: ��� �� ������ �� ������� ������ :: ������ ����� ������ |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 11)
Равенство (1) можно также представить в виде
где
Для анизотропного материала 6 зависимостей между компонентами напряжений и деформаций имеют вид:
............................................................... Из входящих сюда 36 коэффициентов c ijназываются модулями упругости, 21 между собой независимы и характеризуют упругие свойства анизотропного материала. Для нелинейного упругого изотропного материала в равенствах (2) всюду вместо m входит коэффициент
Математическая задача У. т. при равновесии состоит в том, чтобы, зная действующие внешние силы (нагрузки) и т. н. граничные условия, определить значения в любой точке тела компоненты напряжений и деформаций, а также компоненты u x , u y , и z ;вектора перемещения каждой частицы тела, т. е. определить эти 15 величин в виде функций от координат x, у, zточек тела. Исходными для решения этой задачи являются дифференциальные уравнения равновесия:
где r – плотность материала, XYZ –проекции на координатные оси действующей на каждую частицу тела (например, силы тяжести), отнесённые к массе этой частицы. К трём уравнениям равновесия присоединяются 6 равенств (1) в случае изотропного тела и ещё 6 равенств вида:
устанавливающих зависимости между компонентами деформаций и перемещений. Когда на часть S 1граничной поверхности тела действуют заданные поверхностные силы (например, силы контактного взаимодействия), проекции которых, отнесённые к единице площади, равны F x , F y , F z ,а для части S 2этой поверхности заданы перемещения её точек j х ,j у ,j z, граничные условия имеют вид:
где l 1 , l 2 , l 3 –косинусы углов между нормалью к поверхности и координатными осями. Первые условия означают, что искомые напряжения должны удовлетворять на границе S 1трём равенствам (6), а вторые – что искомые перемещения должны удовлетворять на границе S 2равенствам (7); в частном случае может быть j x= j y= j z= 0 (часть поверхности S 2жестко закреплена). Например, в задаче о равновесии плотины массовая сила – сила тяжести, поверхность S 2подошвы плотины неподвижна, на остальной поверхности S 1действуют силы: напор воды, давление различных надстроек, транспортных средств и т.д. В общем случае поставленная задача представляет собой пространственную задачу У. т., решение которой трудно осуществимо. Точные аналитические решения имеются лишь для некоторых частных задач: об изгибе и кручении бруса, о контактном взаимодействии двух тел, о концентрации напряжений, о действии силы на вершину конического тела и др. Т. к. уравнения У. т. являются линейными, то решение задачи о совместном действии двух систем сил получается путём суммирования решений для каждой из систем сил, действующих раздельно (принцип линейной суперпозиции). В частности, если для какого-нибудь тела найдено решение при действии сосредоточенной силы в какой-либо произвольной точке тела, то решение задачи при произвольном распределении нагрузок получается путём суммирования (интегрирования). Такие решения, называются ,получены лишь для небольшого числа тел (неограниченное пространство, полупространство, ограниченное плоскостью, и некоторые др.). Предложен ряд аналитических методов решения пространственной задачи У. т.: вариационные методы (Ритца, Бубнова – Галёркина, Кастильяно и др.), метод упругих потенциалов, метод Бетти и др. Интенсивно разрабатываются численные методы (конечно-разностные, метод конечных элементов и др.). Разработка общих методов решений пространственной задачи У. т. – одна из наиболее актуальных проблем У. т. При решении плоских задач У. т. (когда один из компонентов перемещения равен нулю, а два других зависят только от двух координат) широкое применение находят методы теории функций комплексного переменного. Для стержней, пластин и оболочек, часто используемых в технике, найдены приближённые решения многих практически важных задач на основе некоторых упрощающих предположений. Применительно к этим объектам специфический интерес представляют задачи об устойчивости равновесия (см. ) .
В задаче термоупругости определяются напряжения и деформации, возникающие вследствие неоднородного распределения температуры. При математической постановке этой задачи в правую часть первых трёх уравнений (1) добавляется член
Большой практических интерес представляют задачи У. т. для неоднородных тел. В этих задачах коэффициент l, m в уравнении (1) являются не константами, а функциями координат, определяющими поле упругих свойств тела, которое иногда задают статистически (в виде некоторых функций распределения). Применительно к этим задачам разрабатываются статистические методы У. т., отражающие статистическую природу свойств поликристаллических тел. В динамических задачах У. т. искомые величины являются функциями координат и времени. Исходными для математического решения этих задач являются дифференциальные уравнения движения, отличающиеся от уравнений (4) тем, что правые части вместо нуля содержат инерционные члены
Одной из современных проблем У. т. является математическая постановка задач и разработка методов их решения при конечных (больших) упругих деформациях. Экспериментальные методы У. т. (метод многоточечного тензометрирования, напряжений, метод муаров и др.) позволяют в некоторых случаях непосредственно определить распределение напряжений и деформаций в исследуемом объекте или на его поверхности. Эти методы используются также для контроля решений, полученных аналитическими и численными методами, особенно когда решения найдены при каких-нибудь упрощающих допущениях. Иногда эффективными оказываются экспериментально-теоретические методы, в которых частичная информация об искомых функциях получается из опытов. Лит.:Ляв А., Математическая теория упругости, пер. с англ., М. – Л., 1935; Лейбензон Л. С., Курс теории упругости, 2 изд., М. – Л., 1947; Мусхелишвили Н. И., Некоторые основные задачи математической теории упругости, 5 изд., М., 1966; Трёхмерные задачи математической теории упругости, Тб., 1968; Лурье А. И., Теория упругости, М., 1970; Стретт Дж. В. (лорд Рэлей), Теория звука, пер. с англ., т. 1–2, М., 1955; Теория температурных напряжений, пер. с англ., М., 1964; Снеддон И. Н., Берри Д. С., Классическая теория упругости, пер. с англ., М., 1961; Тимошенко С. П., Гудьер Дж. Н., Теория упругости, пер. с англ., М., 1975. А. А. Ильюшин, В. С. Ленский. Упругость Упру'гость,свойство макроскопических тел сопротивляться изменению их объёма или формы под воздействием механических напряжений. При снятии приложенного напряжения объём и форма упруго деформированного тела восстанавливаются. У. тел обусловлена силами взаимодействия атомов, из которых они построены. В твёрдых телах при температуре абсолютного нуля в отсутствии внешних напряжений атомы занимают равновесные положения, в которых сумма всех сил, действующих на каждый атом со стороны остальных, равна нулю, а потенциальная энергия атома минимальна. Кроме сил притяжения и отталкивания, зависящих только от расстояния ( рис. 1 ) между атомами (центральные силы), в многоатомных молекулах и макроскопических телах действуют также угловые силы, зависящие от т. н. валентных углов между прямыми, соединяющими данный атом с различными его соседями ( рис. 2 ). При равновесных значениях валентных углов угловые силы также уравновешены. Энергия макроскопического тела зависит от межатомных расстояний и валентных углов, принимая минимальное значение при равновесных значениях этих параметров. Под действием внешних напряжений атомы смещаются из своих равновесных положений, что сопровождается увеличением потенциальной энергии тела на величину, равную работе внешних напряжений по изменению объёма и формы тела. После снятия внешних напряжений конфигурация упруго деформированного тела с неравновесными межатомными расстояниями и валентными углами оказывается неустойчивой и самопроизвольно возвращается в равновесное состояние, точнее, атомы колеблются около равновесных положений. Запасённая в теле избыточная потенциальная энергия превращается в кинетическую энергию колеблющихся атомов, т. е. в тепло. Пока отклонения межатомных расстояний и валентных углов от их равновесных значений малы, они пропорциональны действующим между атомами силам, подобно тому как удлинение или сжатие пружины пропорционально приложенной силе. Поэтому тело можно представить как совокупность атомов-шариков, соединённых пружинами, ориентации которых фиксированы др. пружинами ( рис. 2 ). Константы упругости этих пружин определяют материала, а упругая деформация тела пропорциональна приложенному напряжению, т. е. определяется ,который является основой и сопротивления материалов. При конечных температурах (ниже температур плавления) даже без приложения и снятия внешних напряжений атомы совершают малые тепловые колебания около положений равновесия. Это приводит к тому, что модули упругости материала зависят от температуры, но не меняет существа рассмотренных явлений. В жидкости тепловые колебания имеют амплитуду, сравнимую с равновесным расстоянием r 0, вследствие чего атомы легко меняют своих соседей и не сопротивляются касательным напряжениям, если они прикладываются со скоростью, значительно меньшей скорости тепловых колебаний. Поэтому жидкости (как и газы) не обладают упругостью формы. В газообразном состоянии средние расстояния между атомами или молекулами значительно больше, чем в конденсированном. Упругость газов (паров) определяется тепловым движением молекул, ударяющихся о стенки сосуда, ограничивающего объём газа. Лит.:Фейнман Р., Лейтон Р., Сэндс М., Фейнмановские лекции по физике, [в.] 7, М., 1966, гл. 38, 39; Смирнов А. А., Молекулярно-кинетическая теория металлов, М., 1966, гл. 2; Френкель Я. И., Введение в теорию металлов, 4 изд., Л., 1972, гл. 2. А. Н. Орлов. 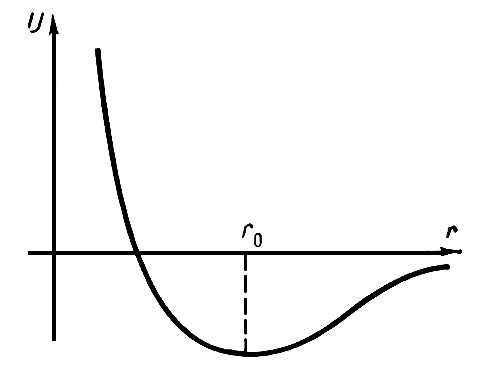
Рис. 1. Зависимость потенциальной энергии взаимодействия двух атомов от расстояния r между ними. Равновесное состояние r 0отвечает наименьшему значению потенциальной энергии. На этом расстоянии силы притяжения и отталкивания между атомами уравновешены. 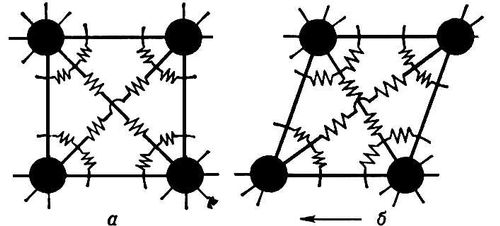
Рис. 2. Шариковая модель элементарной ячейки кубического кристалла: а — в равновесии при отсутствии внешних сил; б — при действии внешнего касательного напряжения. Упругость водяного пара Упру'гость водяно'го па'рав атмосфере, парциальное давление водяного пара, находящегося в воздухе; выражается в мбарили мм рт. ст.(1 мбар =10 2 к/м 3). У. в. п. зависит от количества водяного пара в единице объёма и является одной из характеристик .У. в. п. у земной поверхности может быть около нуля (в Антарктиде, зимой в Якутии, иногда в пустынях) и до 30–35 мбарвблизи экватора. С высотой У. в. п. быстро убывает – в 2 раза в нижних 1,5 кми почти до нуля на верхней границе тропосферы. Упругость насыщения Упру'гость насыще'нияв метеорологии, ,максимально возможная при данной температуре. Она тем больше, чем выше температура воздуха. По достижении У. н. начинается .Над переохлажденной водой У. н. больше, чем над льдом при тех же температурах; над выпуклой водяной поверхностью больше, а над вогнутой меньше, чем над плоской. У. н. при температуре 30 °С не превышает 42,4 мбар,при температуре 0°С – 6,1 мбар,а при – 20 °С равна 1,27 мбарнад водой и 1,03 мбарнад льдом (1 мбар =10 2 н/м 3). Упряжь У'пряжь,сбруя, приспособления для запряжки лошадей или др. упряжных животных (вол, верблюд, олень, собака и др.) с целью управления ими на работах в повозках и с.-х. орудиях, под вьюком, а также в верховой езде. У. для лошади в зависимости от вида запряжки подразделяют на одноконную и пароконную, дуговую и бездуговую. В одноконную дуговую У. входят с гужами и супонью, седёлка с подпругой, чересседельник, подбрюшник, , ,уздечка с удилами и поводьями, вожжи; в одноконную бездуговую – хомут с гужевыми мочками, за которые крепят постромки, вместо гужей ремённые горты, скрепляющие хомут с оглоблями. Пароконная У. для дышловой запряжки состоит из хомутов, нагрудных ремней, постромок, шлей, уздечек с удилами и парных вожжей. В некоторых запряжках хомут заменяют шоркой. Основная часть сбруи верховых лошадей – .Воловая парная У. представляет собой деревянное ярмо, надеваемое на шею и прикрепляемое к дышлу. Верблюжья У. состоит из уздечки, вожжей и шлейки. Оленья и собачья У. в нартах – шлейка с одной постромкой; управляют оленями шестом или одной вожжой. В собачьих У. вожжей нет. Неправильно изготовленная или плохо подогнанная У. вызывает намины и повреждения кожи животного, что снижает его работоспособность. С. В. Афанасьев. Упсала (город в Швеции) У'псала(Uppsala), город в Швеции. Административный центр лена Упсала. 136 тыс. жителей (1974). Крупный промышленный и культурный центр. Машиностроение, полиграфическая, керамическая, пищевая промышленность. Старейший в Швеции университет (основан в 1477). Музей К. ,который жил и похоронен в У. Современный У., первоначально называвшаяся Эстра-Арос (Ostra-Aros), по-видимому, уже в 12 в. была поселением городского типа. В 1273 стала резиденцией архиепископа, с 1280 называется У. До 1719 в У. проходили важнейшие государственные собрания, коронации швед. королей. В 14–18 вв. У. – центр внутренней торговли, место общешведской ярмарки. В конце 19 – начале 20 вв. – оплот консервативных сил Швеции. Город сохранил фрагменты средневековой планировки. Памятники архитектуры – готический собор, крупнейший в Скандинавии (1260–1435), романская церковь Бондчюрка (12 в.), замок (с 1540, архитектор Г. Васа, Ф. Парр), барочный «Густавианум» (1620; до 19 в. – центральное здание университета, ныне музей), ампирные постройки (библиотека университета, 1819–26, архитектор К. Ф. Сундвалль, и др.). К С. от У. – Старая У. (в 1-м тыс. н. э. – языческий культовый центр), где сохранились многочисленные курганы и фрагменты древнейшего в Швеции собора (около 1100), включенные в церковь 13 в. В У. имеется Дисагорден (архитектурный музей на открытом воздухе). Лит.:Liljeroth Е., Brunius Т., Ett bildverk ot Uppsala, Maimo, 1954. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 |
|||||||
 ,
...,(2)
,
...,(2)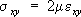 , …,
, …,

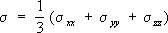 –среднее (гидростатическое) напряжение,
К –модуль всестороннего сжатия.
–среднее (гидростатическое) напряжение,
К –модуль всестороннего сжатия.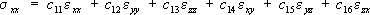 (3)
(3)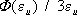 , а соотношение
, а соотношение
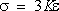 заменяется равенством
заменяется равенством
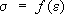 , где величина e
uназывается интенсивностью деформации, а функции
Фи
f, универсальные для данного материала, определяются из опытов. Когда
Ф(e
u) достигает некоторого критического значения, возникают пластические деформации. Законы пластичности при пропорциональном возрастании нагрузок или напряжений (простое нагружение) имеют тот же вид, но с др. значениями функций Ф и
f(законы теории малых упруго-пластических деформаций), а при уменьшении напряжений (разгрузке) имеют место соотношения (1) или (2), в которых вместо s
ijи e
ij
подставляются их приращения (разности двух текущих значений).
, где величина e
uназывается интенсивностью деформации, а функции
Фи
f, универсальные для данного материала, определяются из опытов. Когда
Ф(e
u) достигает некоторого критического значения, возникают пластические деформации. Законы пластичности при пропорциональном возрастании нагрузок или напряжений (простое нагружение) имеют тот же вид, но с др. значениями функций Ф и
f(законы теории малых упруго-пластических деформаций), а при уменьшении напряжений (разгрузке) имеют место соотношения (1) или (2), в которых вместо s
ijи e
ij
подставляются их приращения (разности двух текущих значений).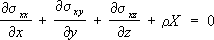 ,
,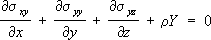 , (4)
, (4)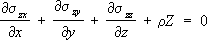
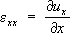 , …,
, …,
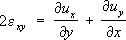 , …, (5)
, …, (5) (на
S
1) (6)
(на
S
1) (6) ,
,
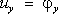 ,
,
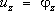 (на
S
2) (7)
(на
S
2) (7)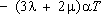 , где a – коэффициент линейного теплового расширения,
T(
x
1
, x
2
, x
3)
–заданное поле температуры. Аналогичным образом строится теория электромагнитоупругости и упругости подвергаемых облучению тел.
, где a – коэффициент линейного теплового расширения,
T(
x
1
, x
2
, x
3)
–заданное поле температуры. Аналогичным образом строится теория электромагнитоупругости и упругости подвергаемых облучению тел.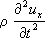 и т.д. К исходным уравнениям должны также присоединяться уравнения (1), (5) и, кроме граничных условий (6), (7), ещё задаваться начальные условия, определяющие, например, распределение перемещении и скоростей частиц тела в начальный момент времени. К этому типу относятся задачи о колебаниях конструкций и сооружений, в которых могут определяться формы колебаний и их возможные смены, амплитуды колебаний и их нарастание или убывание во времени, резонансные режимы, динамические напряжения, методы возбуждения и гашения колебаний и др., а также задачи о распространении упругих волн (сейсмические волны и их воздействие на конструкции и сооружения, волны, возникающие при взрывах и ударах, термоупругие волны и т.д.).
и т.д. К исходным уравнениям должны также присоединяться уравнения (1), (5) и, кроме граничных условий (6), (7), ещё задаваться начальные условия, определяющие, например, распределение перемещении и скоростей частиц тела в начальный момент времени. К этому типу относятся задачи о колебаниях конструкций и сооружений, в которых могут определяться формы колебаний и их возможные смены, амплитуды колебаний и их нарастание или убывание во времени, резонансные режимы, динамические напряжения, методы возбуждения и гашения колебаний и др., а также задачи о распространении упругих волн (сейсмические волны и их воздействие на конструкции и сооружения, волны, возникающие при взрывах и ударах, термоупругие волны и т.д.).