 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (ТО)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ТО) - Чтение (стр. 22)
п.). Внемасштабные Т. у. з. используются для передачи объектов, не выражающихся в масштабе карты, то есть главным образом местных предметов, и воспроизводят их вид сверху или сбоку. Положению этих объектов в натуре должны соответствовать на карте следующие точки Т. у. з.: для знака правильной формы (например, треугольника, обозначающего пункт геодезической сети, круга - цистерну, скважину) - центр фигуры; для знака в виде перспективного рисунка объекта (фабричная труба, монумент) - середина основания фигуры; для знака с прямым углом в основании (ветряной двигатель, бензоколонка) - вершина этого угла; для знака, сочетающего несколько фигур (радиомачта, нефтяная вышка), - центр нижней из них. Линейные Т. у. з. предназначены для изображения с возможной графической точностью таких объектов, как береговые линии, ручьи и канавы, дороги, просеки, ограждения, линии проволочных передач, границы угодий и политико-административные границы. Если какай-либо из данных объектов воспроизводится на карте только с преувеличением по ширине, то его плановое положение фиксируют осью соответствующего знака. Линейными Т. у. з. изображаются также
горизонтали
. Пояснительные Т. у. з. применяются в целях дополнительной характеристики показываемых на карте объектов. Например, точка - для фиксации места определения абсолютных отметок рельефа или относительных превышений (высота кургана, глубина обрыва), различные стрелки - для передачи направления течения рек, пункта измерения глубины болота и др., знаки древесных пород - для показа состава лесонасаждений.
На топографических картах, по мере умельчения их масштаба, однородные Т. у. з. объединяются в группы, последние - в один обобщённый знак и т.д.; в целом систему данных обозначений можно представить в виде усечённой пирамиды, в основании которой лежат знаки для топографических планов масштаба 1 : 500, а на вершине - для обзорно-топографических карт масштаба 1:1000000. Цвета Т. у. з. едины для карт всех масштабов. Штриховые знаки угодий и их контуров, строений, сооружений, местных предметов, опорных пунктов и границ печатаются при издании чёрным цветом, элементов рельефа - коричневым; водоёмы, водотоки, болота и ледники - синим (зеркало вод - светло-синим); площади древесно-кустарниковой растительности - зелёным (карликовые леса, стланики, кустарники, виноградники - светло-зелёным), кварталы с огнестойкими строениями и шоссе - оранжевым, кварталы с неогнестойкими строениями и улучшенные грунтовые дороги - жёлтым. Наряду с Т. у. з. для топографических карт установлены условные сокращения собственных названий политико-административных единиц (например, Московская область - Моск.) и пояснительных терминов (например, электростанция - эл.-ст., юго-западный - ЮЗ, рабочий посёлок - р. п.). Стандартизованные шрифты для надписей на топографических картах позволяют дополнительно к Т. у. з. давать существенные сведения. Например, шрифты для наименований населённых пунктов отображают их тип, политико-административное значение и населённость, для рек - величину и возможность судоходства; шрифты для отметок высот, характеристик перевалов и колодцев дают возможность выделить главные из них и т.д. Т. у. з., условные сокращения надписей и шрифты для топографических карт объединены по группам масштабов в ряд таблиц, модернизируемых в среднем каждые десять лет. Основные из примерно 400 Т. у. з. (применительно к карте масштаба 1 : 25 000) показаны на вклейке к стр. 64-65. Л. М. Гольдман. Топография Топогра'фия(от греч. tо'pos - место и ¼ графия ), научно-техническая дисциплина, занимающаяся географическим и геометрическим изучением местности путём создания топографических карт на основе съёмочных работ (наземных, с воздуха, из космоса). По одним представлениям, Т. - самостоятоятельный раздел картографии , охватывающий проблемы детального общегеографического картографирования территории, по другим - раздел геодезии , посвященный проблемам измерений на земной поверхности и по аэроснимкам (см. Фотограмметрия ) для определения положения, формы и размеров снимаемых природных и социально-экономических объектов. В сферу Т. входят вопросы классификации, содержания и точности топографических карт, методики их изготовления и обновления и получения по ним различной информации о местности. В каждой стране все эти вопросы регламентируются собственными стандартами (связанными с хозяйственно-политическими факторами, организационно-техническими возможностями картографо-геодезических служб и характером ландшафтов), но поскольку в целом они достаточно близки, это позволяет создавать сопоставимые топографические карты. Периодическая модернизация данных стандартов, а также совершенствование базирующихся на них топографических условных знаков и основных положений по отбору и обобщению элементов нагрузки карт (в соответствии с их масштабами и особенностями территории - см. Генерализация картографическая ) составляют одну из важнейших задач Т. Первые съёмочные работы для изготовления топографических карт были выполнены в 16 в. Наземные съёмки, наглядно передающие размещение и особенности объектов местности и базирующиеся на точных инструментальных измерениях, получили развитие в 18 в., аэрофототопографические съёмки - в 1-й трети 20 в., космические - в последней трети 20 в. В настоящее время наземные методы применяются в Т. преимущественно на таких участках, картографирование которых другим путём нерентабельно из-за их малой площади или затруднительно по характеру территории. В первом случае производят мензульную съёмку , выполняемую целиком в натуре, во втором - для ряда горных районов - фототеодолитную съёмку (наземную фотограмметрическую), при которой часть работ ведут на местности с помощью фототеодолита, а часть - камерально на фотограмметрических приборах. Использование в Т. материалов космической съёмки пока ограничивается изготовлением обзорно-топографических и мелкомасштабных топографических карт преимущественно на неосвоенные и малоизученные территории полярных стран, пустынь, джунглей, выявлением и отбором по космическим снимкам таких участков земной поверхности, для которых обычная аэрофотосъёмка, с целью создания или обновления средне- и крупномасштабных топографических карт, должна быть поставлена в первую очередь. Основными в современной Т. являются аэрофототопографические методы (см. Аэрофототопография ) - комбинированный и стереотопографический. При комбинированной съёмке не только аэрофотосъёмочные, но и все топографические работы, а именно: построение плановой и высотной основы карты, рисовка рельефа и дешифрирование на фотоплане предметов и контуров, выполняются непосредственно на местности. При наиболее эффективной стереотопографической съёмке в полёте производят аэрофотографирование и радиогеодезические работы по созданию съёмочного каркаса карты, на местности строят опорную геодезическую сеть , дешифрируют эталонные участки и инструментально наносят неизобразившиеся на аэроснимках объекты. Остальные процессы по изготовлению карты - построение фотограмметрических сетей (для развития её каркаса), стереоскопическую рисовку рельефа и дешифрирование аэрофотоизображения на всю территорию съёмки - осуществляют камеральным путём. Весьма важной задачей Т. является обеспечение сокращения полевых работ, в частности путём совершенствования региональных технологических схем топографической съёмки. Обновление топографических карт, то есть приведение их содержания в соответствие с современными требованиями и состоянием местности, представляет собой самостоятельный, всё более развивающийся метод Т. В зависимости от особенностей района применяют обновление периодическое (от 3-4 до 12-15 лет) или непрерывное; в обоих случаях оно должно базироваться на аэрофотосъёмке и так называемых материалах картографического значения (землеустроительные и лесные планы, ведомости инвентаризации зданий в городах, лоции, линейные графики дорог, схемы линий электропередачи, справочники административно-территориального деления и др.), что позволяет выполнять основной объём работ камеральным путём. Дополнения и исправления при обновлении карт необходимы главным образом по социально-экономическим объектам ландшафта - населённым пунктам, дорогам, обрабатываемым угодьям. Обновленные карты должны иметь такую же точность, что и новые карты, полученные при съёмке в данном масштабе. Для целей обновления карт и в меньшей мере для их создания съёмочными методами, наряду с воздушным черно-белым или цветным фотографированием как основным средством получения информации о местности, стали применять фотоэлектронную аэросъёмку (в частности, радиолокационную). Современный этап развития Т. характеризуется внедрением средств автоматизации в дело создания топографических карт. Практически приемлемые результаты уже получены для процессов считывания с помощью ЭВМ информации с аэроснимков и её записи в цифровой форме, автоматизированного преобразования последней при составлении оригиналов карт (включая трансформирование из центральной проекции в ортогональную, рисовку рельефа в горизонталях, дешифрирование части объектов) на различных приборах и гравировании (или вычерчивании) оригиналов для издания. Наряду с изготовлением карт средства автоматизации применимы в Т. для построения так называемых цифровых моделей местности, то есть формализованных её моделей, представленных координатами и характеристиками точек местности, записанными цифровым кодом (например, на магнитной ленте) для последующей обработки на ЭВМ. Эти модели служат для: 1) дополнения карты данными, не выражающимися ни при графическом, ни при фотографическом воспроизведении местности (см. Фотокарты ), но весьма важными при ряде изысканий и в первую очередь в целях землеустройства и городского строительства; 2) выделения содержащейся на картах информации (объектов того или иного вида, типов территории, комплекса сведений, существенных при решении таких инженерных задач, как выбор трасс каналов, дорог и трубопроводов, участков под водохранилища, аэродромы, лесопосадки и т.п.). Цифровая форма даёт также возможность кодирования и поиска необходимых материалов картографического значения при их сосредоточении в справочно-информационных фондах. Автоматизация дистанционных методов получения топографической информации позволила приступить к съёмке поверхности Луны и части планет с изготовлением блоков обзорно-топографических карт на большие площади, отдельных листов собственно топографических карт на избранные участки и крупномасштабных планов на местность вокруг пунктов посадки межпланетных автоматических станций и космических кораблей, а также по трассам луноходов. Лит.:50 лет советской геодезии и картографии, М., 1967; Альбом образцов изображения рельефа на топографических картах, М., 1968; Подобедов Н. С., Полевая картография, М., 1970; Салищев К. А., Картография, 2 изд., М., 1971; Куприн А. М., Говорухин А. М., Гамезо М. В., Справочник по военной топографии, М., 1973: Картография с основами топографии, под ред. А. В. Гедымина, ч. 1-2, М., 1973; Соколова Н. А.. Фотограмметрические методы топографического картографирования, в кн.: Итоги науки и техники. Геодезия и аэросъёмка, т. 8, М., 1973; Лобанов А. Н., Аэрофототопография, М., 1971; Материалы Всесоюзной конференции по проблемам крупномасштабных топографических съёмок (Москва, 1973), М., 1974; Господ и нов Г. В., Сорокин В. Н., Топография, 2 изд., М., 1974; Гольдман Л. М., Совершенствование содержания топографических карт и планов, предназначенных для мелиорации земель, «Геодезия и картография», 1974, № 4; Салищев К. А., Картоведение, М., 1976: Поспелов Е. М., Картографическая изученность зарубежных стран, М., 1975. Л.М. Гольдман. Топография барическая Топография бари'ческая, распределение высот или геопотенциалов той или иной изобарической поверхности над уровнем моря (абсолютная Т. б. ) или над уровнем другой нижележащей изобарической поверхности (относительная Т. б.). Топография военная Топогра'фия вое'нная,см. Военная топография . Топозеро Топо'зеро,озеро в северной части Карельской АССР. Площадь 986 км 2. Расположено на высоте 109 м. Вытянуто с С.-С.-З. на Ю.-Ю.-В. Берега, особенно восточный, изрезанные; на Т. много островов, общая площадь 63 км 2. Питание преимущественно снеговое. Высшие уровни в июне, низшие в апреле. Замерзает в конце октября - ноябре, вскрывается в мае. С созданием Кумской ГЭС в 1966 стало частью Кумского водохранилища . Лесосплав. Лов рыбы (ряпушка, хариус, сиг, корюшка и др.). Топологическая психология Топологи'ческая психоло'гия,психологическая концепция немецко-американского психолога К. Левина, представляющая собой применение понятий топологии к разработанной им теории психологического «поля». Развита в 1930-х гг. Включает как собственно математические, так и психологические понятия, с помощью которых описываются статические и динамические особенности психологического поля. См. ст. Левин К. и литературу при ней. Топологическое пространство Топологи'ческое простра'нство,множество, состоящее из элементов любой природы, в котором тем или иным способом определены предельные соотношения. Предельные соотношения, наличие которых превращает данное множество Хв топологическое пространство, состоят в том, что для каждого подмножества Амножества Хопределено его замыкание, то есть множество [ А], состоящее из всех элементов множества Аи из предельных точек этого множества (если какое-либо множество является Т.п., то его элементы, независимо от их действительной природы, принято называть точками данного Т.п.). «Ввести в данное множество Хтопологию», или «превратить данное множество Хв Т. п.», - это значит тем или иным способом указать замыкание [ А] для каждого подмножества Амножества Х. Точки множества [А] называются точками прикосновения множества А. Каждое метрическое пространство может быть естественным образом превращено в Т. п., поэтому говорят (допуская некоторую неточность), что метрическое пространство является частным случаем топологического. В частности, числовая прямая, евклидово пространство любого числа измерений, различные функциональные пространства могут служить примерами метрических и, следовательно, топологических пространств. Существует много способов вводить в данное множество Хтопологию, то есть превращать его в Т. п.; например, в случае метрических пространств топология вводится посредством вспомогательного понятия расстояния. В очень многих случаях топология в данное множество Хвводится посредством окрестностей: для каждого элемента (для каждой «точки») множества Хнекоторые подмножества множества Хвыделяются в качестве окрестностей данной точки. В предположении, что окрестности определены, точка хобъявляется точкой прикосновения множества А,если каждая окрестность этой точки содержит хотя бы одну точку множества А.См. также ст. Топология и литературу при ней. Топология Тополо'гия(от греч. tо'pos - место и ¼ логия ) -часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных подходов к её изучению привели к распадению единой Т. на ряд отделов («общая Т.», «алгебраическая Т.» и др.), отличающихся друг от друга по предмету и методу изучения и фактически весьма мало между собой связанных. I. Общая топология Часть Т., ориентированная на аксиоматическое изучение непрерывности, называется общей Т. Наряду с алгеброй общая Т. составляет основу современного теоретико-множественного метода в математике. Аксиоматически непрерывность можно определить многими (вообще говоря, неравносильными) способами. Общепринята аксиоматика, основывающаяся на понятии открытого множества. Топологической структурой, или топологией, на множестве Хназывают такое семейство его подмножеств, называемых открытыми множествами, что: 1) пустое множество Ж и всё Хоткрыты; 2) объединение любого числа и пересечение конечного числа открытых множеств открыто. Множество, на котором задана топологическая структура, называют топологическим пространством.В топологическом пространстве Хможно определить все основные понятия элементарного анализа, связанные с непрерывностью. Например, окрестностью точки xО Xназывают произвольное открытое множество, содержащее эту точку; множество AМ Xназывают замкнутым, если его дополнение Х\ Аоткрыто; замыканием множества Аназывают наименьшее замкнутое множество, содержащее A; если это замыкание совпадает с X, то Аназывают всюду плотным в Хи т.д. По определению, Ж и Хявляются одновременно замкнутыми и открытыми множествами. Если в Хнет других множеств, одновременно замкнутых и открытых, то топологическое пространство Хназывают связным. Наглядно связное пространство состоит из одного «куска», а несвязное - из нескольких. Любое подмножество
Атопологического пространства
Хобладает естественной топологической структурой, состоящей из пересечений с
Аоткрытых множеств из
X. Снабженное этой структурой
Аназывают подпространством пространства
X. Каждое
метрическое пространство
становится топологическим, если за его открытые множества принять множества, содержащие вместе с произвольной точкой некоторую её e-окрестность (шар радиуса e с центром в этой точке). В частности, любое подмножество
n-мерного евклидова пространства
Геометрическая Т. довольно четко распадается на две части: изучение подмножеств
Открытым покрытием топологического пространства
Хназывают семейство его открытых множеств, объединением которого является всё
X. Топологическое пространство
Хназывают компактным (в другой терминологии -бикомпактным), если любое его открытое покрытие содержит конечное число элементов, также образующих покрытие. Классическая теорема Гейне - Бореля утверждает, что любое ограниченное замкнутое подмножество
Открытое покрытие { V b} называют вписанным в покрытие { U a}, если для любого b существует a такое, что V bМ U a .Покрытие { V b} называют локально конечным, если каждая точка хО Хобладает окрестностью, пересекающейся только с конечным числом элементов этого покрытия. Топологическое пространство называют паракомпактным, если в любое его открытое покрытие можно вписать локально конечное покрытие. Класс паракомпактных пространств является примером классов топологических пространств, получающихся наложением так называемых условий типа компактности. Этот класс очень широк, в частности он содержит все метризуемые топологические пространства, то есть пространства X, в которых можно ввести такую метрику r, что Т., порожденная r в X,совпадает с Т., заданной в X. Кратностью открытого покрытия называют наибольшее число
kтакое, что найдётся
kего элементов, имеющих непустое пересечение. Наименьшее число
n,обладающее тем свойством, что в любое конечное открытое покрытие топологического пространства
Хможно вписать открытое покрытие кратности Ј
n+ 1, обозначается символом dim
Хи называется размерностью
X. Это название оправдано тем, что в элементарно-геометрических ситуациях dim
Хсовпадает с обычно понимаемой размерностью, например dim
Важные классы топологических пространств получаются наложением так называемых аксиом отделимости. Примером является так называемая аксиома Хаусдорфа, или аксиома T 2, требующая, чтобы любые две различные точки обладали непересекающимися окрестностями. Топологическое пространство, удовлетворяющее этой аксиоме, называется хаусдорфовым, или отделимым. Некоторое время в математической практике встречались почти исключительно хаусдорфовы пространства (например, любое метрическое пространство хаусдорфово). Однако роль нехаусдорфовых топологических пространств в анализе и геометрии постоянно растет. Топологические пространства, являющиеся подпространствами хаусдорфовых (би) компактных пространств, называются вполне регулярными или тихоновскими. Их тоже можно охарактеризовать некоторой аксиомой отделимости, а именно: аксиомой, требующей, чтобы для любой точки
x
0
Топологические пространства, являющиеся открытыми подпространствами хаусдорфовых компактных, называются локально компактными пространствами. Они характеризуются (в классе хаусдорфовых пространств) тем, что каждая их точка обладает окрестностью с компактным замыканием (пример: евклидово пространство). Любое такое пространство дополняется одной точкой до компактного (пример: присоединением одной точки из плоскости получается сфера комплексного переменного, а из
Отображение f : X® Yтопологическое пространства Хв топологическое пространство Yназывают непрерывным отображением, если для любого открытого множества VМ Yмножество f -1( V) открыто в X. Непрерывное отображение называют гомеоморфизмом, если оно взаимно однозначно и обратное отображение f -1: Y® Xнепрерывно. Такое отображение устанавливает взаимно однозначное соответствие между открытыми множествами топологических пространств Хи Y, перестановочное с операциями объединения и пересечения множеств. Поэтому все топологические свойства (то есть свойства, формулируемые в терминах открытых множеств) этих пространств одни и те же, и с топологической точки зрения гомеоморфные топологические пространства (то есть пространства, для которых существует хотя бы один гомеоморфизм Х® Y) следует считать одинаковыми (подобно тому как в евклидовой геометрии одинаковыми считаются фигуры, которые можно совместить движением). Например, гомеоморфны («топологически одинаковы») окружность и граница квадрата, шестиугольника и т.п. Вообще любые две простые (не имеющие двойных точек) замкнутые линии гомеоморфны. Напротив, окружность не гомеоморфна прямой (ибо удаление точки не нарушает связности окружности, но нарушает связность прямой; по той же причине прямая не гомеоморфна плоскости, а окружность не гомеоморфна «восьмёрке»). Окружность не гомеоморфна также и плоскости (выкиньте не одну, а две точки). Пусть {
Х
a} - произвольное семейство топологических пространств. Рассмотрим множество
Хвсех семейств вида {
х
a}
,где
x
a
Если
Х- топологическое пространство, а
Y- произвольное множество и если задано отображение
p:
X®
Yпространства
Хна множество
Y(например, если
Yявляется фактормножеством
Хпо некоторому отношению эквивалентности, а
pпредставляет собой естественную проекцию, сопоставляющую с каждым элементом
хО
Хего класс эквивалентности), то можно ставить вопрос о введении в
Yтопологической структуры, относительно которой отображение
pнепрерывно. Наиболее «богатую» (открытыми множествами) такую структуру получают, полагая открытыми множествами в
Yвсе те множества
VМ
Y,для которых множество
f
1(
V) М
Хоткрыто в
X. Снабженное этой топологической структурой множество
Yназывается факторпространством топологического пространства
Х(по отношению к
p). Оно обладает тем свойством, что произвольное отображение
f:
Y®
Zтогда и только тогда непрерывно, когда непрерывно отображение
Пусть Х- топологическое пространство, А- его подпространство и f: A® Y- непрерывное отображение. Предполагая топологические пространства Хи Yнепересекающимися, введём в их объединении ХИ Yтопологическую структуру, считая открытыми множествами объединения открытых множеств из Хи Y. Далее, введём в пространстве ХИ Yнаименьшее отношение эквивалентности, в котором a~ f(a)для любой точки aО А. Соответствующее факторпространство обозначается символом XИ fY, и о нём говорят, что оно получено приклеиванием топологического пространства Хк топологическому пространству Yпо Апосредством непрерывного отображения f. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36 |
|||||||
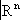 является топологическим пространством. Теория таких пространств (под названием «геометрической Т.») и теория метрических пространств включаются по традиции в общую Т.
является топологическим пространством. Теория таких пространств (под названием «геометрической Т.») и теория метрических пространств включаются по традиции в общую Т.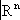 произвольной сложности, подчинённых тем или иным ограничениям общего характера (примером является так называемая теория континуумов, то есть связных ограниченных замкнутых множеств), и изучение способов, какими в
произвольной сложности, подчинённых тем или иным ограничениям общего характера (примером является так называемая теория континуумов, то есть связных ограниченных замкнутых множеств), и изучение способов, какими в
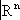 могут быть вложены такие простые топологические пространства, как сфера, шар и т.п. (вложения в
могут быть вложены такие простые топологические пространства, как сфера, шар и т.п. (вложения в
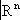 , например, сфер могут быть очень сложно устроенными).
, например, сфер могут быть очень сложно устроенными).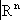 компактно. Оказывается, что все основные теоремы элементарного анализа об ограниченных замкнутых множествах (например, теорема Вейерштрасса о том, что на таком множестве непрерывная функция достигает своего наибольшего значения) справедливы для любых компактных топологических пространств. Это определяет фундаментальную роль, которую играют компактные пространства в современной математике (особенно в связи с теоремами существования). Выделение класса компактных топологических пространств явилось одним из крупнейших достижений обшей Т., имеющих общематематическое значение.
компактно. Оказывается, что все основные теоремы элементарного анализа об ограниченных замкнутых множествах (например, теорема Вейерштрасса о том, что на таком множестве непрерывная функция достигает своего наибольшего значения) справедливы для любых компактных топологических пространств. Это определяет фундаментальную роль, которую играют компактные пространства в современной математике (особенно в связи с теоремами существования). Выделение класса компактных топологических пространств явилось одним из крупнейших достижений обшей Т., имеющих общематематическое значение.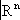 =
n. Возможны и др. числовые функции топологического пространства
X, отличающиеся от dim
X, но в простейших случаях совпадающие с dim
X. Их изучение составляет предмет общей теории размерности - наиболее геометрически ориентированной части общей Т. Только в рамках этой теории удаётся, например, дать чёткое и достаточно общее определение интуитивного понятия геометрической фигуры и, в частности, понятия линии, поверхности и т.п.
=
n. Возможны и др. числовые функции топологического пространства
X, отличающиеся от dim
X, но в простейших случаях совпадающие с dim
X. Их изучение составляет предмет общей теории размерности - наиболее геометрически ориентированной части общей Т. Только в рамках этой теории удаётся, например, дать чёткое и достаточно общее определение интуитивного понятия геометрической фигуры и, в частности, понятия линии, поверхности и т.п. Хи любого не содержащего её замкнутого множества
F
Хи любого не содержащего её замкнутого множества
F
 Хсуществовала непрерывная функция
g : Х®
[0, 1], равная нулю в
x
0и единице на
F.
Хсуществовала непрерывная функция
g : Х®
[0, 1], равная нулю в
x
0и единице на
F.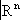 - сфера
S
n).
- сфера
S
n). X
a(прямое произведение множеств
X
a). Для любого a формула
X
a(прямое произведение множеств
X
a). Для любого a формула
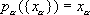 определяет некоторое отображение
определяет некоторое отображение
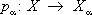 (называется проекцией). Вообще говоря, в
Хможно ввести много топологических структур, относительно которых все отображения
p
aнепрерывны. Среди этих структур существует наименьшая (то есть содержащаяся в любой такой структуре). Снабженное этой топологической структурой множество
Хназывается топологическим произведением топологических пространств
Х
aи обозначается символом
ПХ
a(а в случае конечного числа сомножителей - символом
X
1ґ ... ґ
X
n). В явном виде открытые множества пространства
Хможно описать как объединения конечных пересечений всех множеств вида
(называется проекцией). Вообще говоря, в
Хможно ввести много топологических структур, относительно которых все отображения
p
aнепрерывны. Среди этих структур существует наименьшая (то есть содержащаяся в любой такой структуре). Снабженное этой топологической структурой множество
Хназывается топологическим произведением топологических пространств
Х
aи обозначается символом
ПХ
a(а в случае конечного числа сомножителей - символом
X
1ґ ... ґ
X
n). В явном виде открытые множества пространства
Хможно описать как объединения конечных пересечений всех множеств вида
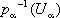 , где
U
aоткрыто в
X
a. Топологическое пространство
Хобладает следующим замечательным свойством универсальности, однозначно (с точностью до гомеоморфизма) его характеризующим: для любого семейства непрерывных отображений
f
a:
Y®
X
aсуществует единственное непрерывное отображение
f:
Y®
X, для которого
, где
U
aоткрыто в
X
a. Топологическое пространство
Хобладает следующим замечательным свойством универсальности, однозначно (с точностью до гомеоморфизма) его характеризующим: для любого семейства непрерывных отображений
f
a:
Y®
X
aсуществует единственное непрерывное отображение
f:
Y®
X, для которого
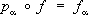 при всех a. Пространство
при всех a. Пространство
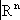 является топологическим произведением
nэкземпляров числовой прямой. Одной из важнейших теорем общей Т. является утверждение о том, что топологическое произведение компактных топологических пространств компактно.
является топологическим произведением
nэкземпляров числовой прямой. Одной из важнейших теорем общей Т. является утверждение о том, что топологическое произведение компактных топологических пространств компактно.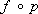 :
X®
Z.Непрерывное отображение
p:
X®
Yназывается факторным, если топологическое пространство
Yявляется по отношению к
pфакторпространством топологического пространства
X. Непрерывное отображение
p:
X®
Yназывается открытым, если для любого открытого множества
UМ
Хмножество
p(U)открыто в
Y, и замкнутым, если для любого замкнутого множества
FМ
Хмножество
p(F)замкнуто в
Y. Как открытые, так и замкнутые непрерывные отображения
f:
Х®
Y, для которых
f(X)=
Y, являются факторными.
:
X®
Z.Непрерывное отображение
p:
X®
Yназывается факторным, если топологическое пространство
Yявляется по отношению к
pфакторпространством топологического пространства
X. Непрерывное отображение
p:
X®
Yназывается открытым, если для любого открытого множества
UМ
Хмножество
p(U)открыто в
Y, и замкнутым, если для любого замкнутого множества
FМ
Хмножество
p(F)замкнуто в
Y. Как открытые, так и замкнутые непрерывные отображения
f:
Х®
Y, для которых
f(X)=
Y, являются факторными.