 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ТЕ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ТЕ) - Чтение (стр. 29)
Роман «За бегущим днём» (1959), повести «Чудотворная» (1958; одноименный фильм, 1960; инсценировка Московского театра «Современник» под назв. «Без креста», 1963), «Весенние перевертыши» (1973), «Ночь после выпуска» (1974) ставят сложные вопросы воспитания. Т.- автор романа «Свидание с Нефертити» (1964) о нравственно-эстетических исканиях молодого художника, вчерашнего фронтовика, в послевоенные годы, научно-фантастической повести «Путешествие длиной в век» (1964), пьес «Белый флаг» (1962, совместно с К. Икрамовым), «Совет да любовь» (1973). Произведения Т. неоднократно вызывали дискуссии в критике и педагогических кругах. Переведены на языки народов СССР и иностранные языки. Т. награжден 2 орденами.
Соч.: Избранные произведения. т. 1-2, М.. 1963; Поденка - век короткий. Чудотворная. Чрезвычайное. Короткое замыкание. Онега. М.. 1969; Свидание с Нефертити. Находка. Костры на снегу, М.. 1970.
Лит.:Клюсов Б.. На передней линии. Очерк творчества Владимира Тендрякова, Минск, 1963; Нинов А.. Современный рассказ. Из наблюдений над русской прозой (1956-66), Л.. 1969; Русские советские писатели-прозаики. Биобиблиографический указатель, т. 5, М.. 1968. А. А. Нинов. Тендюрюк Тендюрю'к(Tendьrьk), вулкан на Армянском нагорье (хребет Аладаг) на В. Турции, близ границы с Ираном. Высота 3542 м.Имеет 3 кратера; находится в сольфатарной стадии (близ вершины - выходы пара и сернистых газов). Теневая птица Тенева'я пти'ца,молотоглав (Scopus umbretta), единственный вид семейства молотоглавов отряда голенастых птиц. Длина тела около 55 см.Клюв сильно сжат с боков. Оперение темно-бурое с более светлыми полосами и пятнами. Распространена в тропической Африке, на Мадагаскаре и на Ю.-З. Аравийского полуострова. Селится в лесах по берегам водоёмов. Гнёзда до 2 мв диаметре, закрытые, трёхкамерные, с узким (около 15 см) ходом, построены из сучьев, травы и грязи на нижних развилках прибрежных деревьев, изредка в расщелинах скал. 3-5 белых яиц откладывают в верхней камере гнезда, насиживают 21 сут;птенцы покидают гнездо через 7 нед.Питаются водными насекомыми, рачками, лягушками. 
Рис. к ст. Теневая птица. Теневой электронный микроскоп Тенево'й электро'нный микроско'п,см. . Теневыносливые растения Теневыно'сливые расте'ния,растения (главным образом древесные, многие травянистые под пологом лиственных пород, тепличные и др.), выносящие некоторое затенение, но хорошо развивающиеся и на прямом солнечном свету. С возрастом, а также в высоких широтах, горах, в более сухом климате теневыносливость понижается. Физиологически Т. р. характеризуются относительно невысокой интенсивностью .Листья Т. р. имеют ряд анатомо-морфологических особенностей: слабо дифференцирована столбчатая и губчатая паренхима, клетки содержат небольшое число (10-40) хлоропластов, величина поверхности которых колеблется в пределах 2-6 см 2на 1 см 2площади листа. Ряд растений под пологом леса (например, копытень, сныть и др.) ранней весной, до распускания листьев древесного яруса, физиологически светолюбивы, а летом, при сомкнувшемся пологе, - теневыносливы. Сравни . Тенезмы Тене'змы(греч. teinesmуs - тщетный позыв, от tйino - напрягаю), болезненные ложные позывы на дефекацию или мочеиспускание. Обусловлены тоническим сокращением мышц прямой кишки или мочевого пузыря; одновременное спастическое сокращение сфинктеров препятствует опорожнению органа. Т. наблюдаются при ,патологических процессах в прямой кишке (воспаление, трещины слизистой оболочки заднего прохода, ,опухоль) или в мочевом пузыре и соседних с ним органах ( , ) ,при заболеваниях спинного мозга ( , ) .Лечение: устранение основной причины, вызывающей появление Т.; сидячие ванны, микроклизмы (настой ромашки, вазелиновое масло), свечи с антиспастическими препаратами. Теней эффект Тене'й эффе'кт,возникновение характерных минимумов интенсивности (теней) в угловом распределении частиц, вылетающих из узлов решётки .Т. э. наблюдается для положительно заряженных тяжёлых частиц (протонов, дейтронов, более тяжёлых ионов). Тени образуются в направлениях кристаллографических осей и плоскостей. Появление тени в направлении кристаллографической оси (осевая тень) обусловлено отклонением частиц, первоначально вылетевших в направлении этой оси, внутриатомным электрическим полем ближайших к излучающему узлу атомов, расположенных в той же цепочке ( рис. 1 ). Распределение относительной интенсивности частиц у в области тени изображено на рис. 2 . Угловые размеры тени определяются соотношением:
где 2 x 0- полуширина тени, eZ 1и Е- заряд и энергия движущейся частицы, eZ 2- заряд ядра атома кристалла, l- расстояние между соседними атомами цепочки. Интенсивность g потока частиц в центре тени для совершенного кристалла (без дефектов) примерно в 100 раз меньше, чем на периферии. Т. э. был обнаружен в 1964 независимо А. Ф. Тулиновым (СССР) и Б. Домеем и К. Бьёрквистом (Швеция), причём частицы, в пучке которых наблюдались тени, в этих работах имели различное происхождение. В экспериментах Тулинова это были продукты ядерных реакций на ядрах кристаллической мишени под действием ускоренных частиц. Домей и Бьёрквист вводили a-радиоактивные ядра в узлы кристаллической решётки (методом ионной имплантации) и наблюдали тени в угловом распределении вылетающих из кристалла a-частиц. Первый метод оказался более универсальным, и практически все последующие эксперименты проводились по его схеме. В частности, с помощью этого метода удалось наблюдать плоскостные тени, то есть области пониженной интенсивности частиц в направлении кристаллографических плоскостей, имеющие форму прямых линий. При регистрации плоскостных теней в качестве детектора часто используют ,так как с их помощью можно регистрировать теневую картину в большом телесном угле. На эмульсии возникает сложная теневая картина кристалла, называемая ионограммой ( рис. 3 ). Расположение пятен и линий на ионограмме зависит от структуры кристалла и геометрических условий опыта. Распределение интенсивности в пределах одной тени (осевой или плоскостной) определяется многими факторами (состав и структура кристалла, сорт и энергия движущихся частиц, температура кристалла, количество дефектов в кристалле). Пятна и линии на ионограмме по своей природе принципиально отличны от пятен и линий, получаемых при изучении кристалла дифракционными методами (см. , , ) .Из-за малой величины длины волны де Бройля для тяжёлых частиц дифракционные явления на образование теней практически не влияют. Т. э. используется в ядерной физике и физике твёрдого тела. На базе Т. э. разработан метод измерения времени протекания
в диапазоне значений 10
-6-10
-18
сек.Информация о величине t извлекается из формы теней в угловых распределениях заряженных продуктов ядерных реакций, поскольку эта форма определяется смещением составного ядра за время его жизни из узла решётки. В физике твёрдого тела Т. э. используется для исследования структуры кристалла, распределения примесных атомов и дефектов. Особенно эффективными методы, основанные на Т. э., оказываются при изучении тонких монокристаллических слоев вещества (10-1000
Т. э. относится к группе ориентационных явлений, возникающих при взаимодействии частиц с кристаллами. Другое ориентационное явление - . Лит.:Тулинов А. Ф., Влияние кристаллической решетки на некоторые атомные и ядерные процессы, «Успехи физических наук», 1965, т. 87, в. 4, с. 585; Широков Ю. М., Юдин Н. П., Ядерная физика, М., 1972; Медиков Ю. В., Тулинов А. Ф., Ядерные столкновения и кристаллы, «Природа», 1974, № 10; Карамян С. А., Меликов Ю. В., Тулинов А. Ф., Об использовании эффекта теней для измерения времени протекания ядерных реакций, «Физика элементарных частиц и атомного ядра», 1973, т. 4, в. 2. А. Ф. Тулинов. 
Рис. 1. Происхождение эффекта теней. 
Рис. 3. Ионограмма кристалла. 
Рис. 2. Угловое распределение интенсивности потока вылетающих из кристалла частиц при эффекте теней. Тенерифе Тенери'фе(Tenerife), вулканический остров в Атлантическом океане, в группе .Территория Испании. Площадь 1946 км 2.Население свыше 500 тыс. чел. (1970). Сложен базальтами. высотой до 3718 м(вулкан Тейде). Климат тропический. Вечнозелёные кустарники и леса. Тропическое земледелие (бананы, цитрусовые, табак, виноград и др.). Рыболовство. Главный город - Санта-Крус-де-Тенерифе. Климатические курорты. Тензодатчик Тензода'тчик, деформации твёрдого тела, вызываемой механическими напряжениями, в сигнал (обычно электрический), предназначенный для последующей передачи, преобразования и регистрации. Наибольшее распространение получили Т. сопротивления, выполненные на базе тензорезисторов (ТР), действие которых основано на их свойстве изменять под влиянием деформации (растяжения или сжатия) своё электрическое сопротивление (см. ) .Конструктивно ТР представляет собой либо решётку ( рис. 1 ), изготовленную из проволоки или фольги (из константана, нихрома, различных сплавов на основе Ni, Mo, Pt), либо пластинку из полупроводника, например, Si. ТР механически жестко соединяют (например, приклеивают, приваривают) с упругим элементом Т. ( рис. 2 ) либо крепят непосредственно на исследуемой детали. Упругий элемент воспринимает изменения исследуемого параметра х(давления, деформации узла машины, ускорения и т. п.) и преобразует их в деформацию решётки (пластинки) e( x), что приводит к изменению сопротивления ТР на величину D R(e) = ± kЧR 0 Чe ,где R 0 -начальное сопротивление ТР, k- коэффициент тензочувствительности (для проволочных Т. k Ј 2-2,5, для полупроводниковых k ~200). Т. сопротивления обычно работают в области упругих деформаций - при e Ј 10 -3 . Величина D
Rзависит не только от e, но и от температуры упругого элемента: D
R(q) = a
ЧDq
Ч R
0,где Dq - изменение температуры упругого элемента, a - температурный коэффициент относительного изменения сопротивления ТР: для проволочных и фольговых ТР a = (2-7)Ч10
-3K
-1. Для уменьшения погрешности требуется автоматическое введение поправок на температуру либо термокомпенсация. Наиболее распространён метод «схемной» термокомпенсации с использованием
.На
рис. 3
показан пример включения в мостовую цепь двух идентичных ТР, воспринимающих деформацию упругого элемента; при этом D
R
1(e) и D
R
2(e) имеют разные знаки, тогда как D
R
1(q) и D
R
2(q) - один и тот же знак. Ток в диагонали моста (выходной сигнал Т.) при условии
Лит.:Туричин А. М., Электрические измерения неэлектрических величин, 4 изд., М.-Л., 1966; Глаговский Б. А., Пивен И. Д., Электротензометры сопротивления, 2 изд., Л., 1972. А. В. Кочеров. 
Рис. 3. Схема включения двух тензорезисторов в мостовую цепь: R 1+ DR 1(e) + DR 1(q) и R 2- DR 2(e) + DR 2(q) - сопротивления тензорезисторов [DR(e) и DR(q) - изменения сопротивлений тензорезисторов в зависимости от изменения деформации e и от температуры q]; R 3, R 4- сопротивления обычных резисторов; i aб- ток в диагонали моста; U - источник питания (постоянного тока); У - усилитель; Р - устройство, регистрирующее результат измерения. 
Рис. 2. Схема тензорезисторного датчика: 1 - решётки; 2 - упругий элемент; R1,..., R4 - тензорезисторы; х - измеряемый параметр. 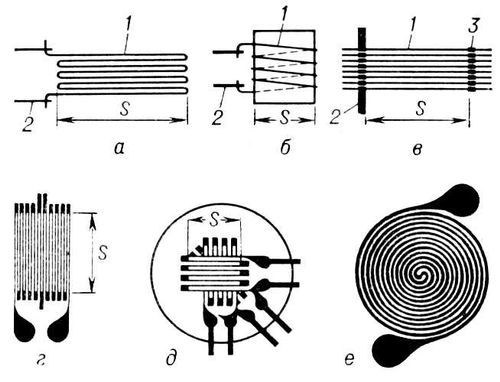
Рис. 1. Рещетки тензодатчиков: проволочные - петлевая (а), витковая (б) и с перемычками (в); фольговые - для изменения одной компоненты деформации (г), трех компонент (д) и кольцевых деформаций (е); 1 - проволока; 2 - выводы решетки; 3 - перемычки; S - база датчика. Тензометр Тензо'метр(от лат. tensus - напряжённый и ) ,прибор для измерения деформаций, вызываемых механическими напряжениями в твёрдых телах. Применяется при исследовании распределения деформаций в деталях машин, конструкций и сооружений, а также при механических испытаниях материалов. Наиболее распространены электротензометры сопротивления, основным элементом которых служит тензорезисторный датчик (см. ) . Тензор Те'нзор(от лат. tensus - напряжённый, натянутый), математический термин, появившийся в середине 19 в. и с тех пор применяющийся в двух различных смыслах. Наибольшее распространение термин «Т.» получил в современном ,где это название присваивается особого рода величинам, преобразующимся по особому закону. В механике, особенно в теории упругости, термин «Т.» широко применяется как синоним симметрического аффинора, то есть линейного оператора Ф, преобразующего вектор хв вектор Фх,и симметрического в том смысле, что скалярное произведение уФхне меняется при перестановке векторов хи у.Здесь термин был первоначально связан с малыми растяжениями (и сжатиями), возникающими при упругой деформации (откуда и название «Т.»), а затем перенесён в другие области механики. Так появились Т. деформации, Т. напряжения, Т. инерции и др. Тензорезистивный эффект
Тензорезисти'вный эффе'кт,изменение удельного электросопротивления твёрдого проводника (
,
) в результате его деформации. Величина относительного изменения компонент тензора электросопротивления
Т. э. связан с изменением межатомных расстояний при деформации, что влечёт за собой изменение структуры энергетических зон кристалла. Последнее обусловливает изменение концентрации носителей тока (электронов проводимости, дырок), их эффективной массы, перераспределение их между энергетическими максимумами в зоне проводимости и минимумами в валентной зоне. Кроме того, деформация влияет на процессы рассеяния носителей (появление новых дефектов, изменение фононного спектра). Т. э. применяется в сопротивлений, служащих для измерения деформаций. Лит.:Блатт Фр. Д ж., Физика электронной проводимости в твердых телах, пер. с англ., М., 1971; Киреев П. С., Физика полупроводников, М., 1969: Ильинская Л. С., Подмарьков А. Н., Полупроводниковые тензодатчики, М.- Л., 1966; Глаговский Б. А., Пивен И. Д., Электротензометры сопротивления, 2 изд., Л., 1972. Б. А. Аронзон. Тензорное исчисление Те'нзорное исчисле'ние,математическая теория, изучающая величины особого рода - тензоры, их свойства и правила действий над ними. Т. и. является развитием и обобщением и теории .Т. и. широко применяется в дифференциальной геометрии, теории римановых пространств, теории относительности, механике, электродинамике и других областях науки. Для описания многих физических и геометрических фактов обычно вводится та или иная система координат, что позволяет описывать различные объекты при помощи одного или нескольких чисел, а соотношения между объектами - равенствами, связывающими эти числа или системы чисел. Некоторые из величин, называемые скалярными (масса, температура и т. д.), описываются одним числом, причём значение этих величин не изменяется при переходе от одной системы координат к другой (мы рассматриваем здесь физические явления с точки зрения классической физики). Другие величины - векторные (сила, скорость и т. д.), описываются тремя числами (компонентами вектора), причём при переходе от одной системы координат к другой компоненты вектора преобразуются по определённому закону. Наряду со скалярными и векторными величинами встречаются во многих вопросах физики и геометрии величины более сложного строения. Эти величины, называемые тензорными, описываются в каждой системе координат несколькими числами (компонентами тензора), причём закон преобразования этих чисел при переходе от одной системы координат к другой более сложен, чем для векторов (точные определения будут даны ниже). При введении координатной системы, помимо чисел, описывающих сам объект или физическое явление, появляются числа, описывающие его связь с выбранной системой координат. Рассмотрим, например, совокупность чисел
J
ij(
i, j =1, 2, 3), где
J
ij - осевой
твёрдого тела относительно оси
X
i,a
J
ij,(при
i¹
j)
-центробежные моменты инерции, взятые с обратным знаком. При переходе от одной системы координат к другой осевой момент инерции
J
iiменяется (так как меняется положение оси
x
iотносительно тела), а потому
J
iiне может рассматриваться как физическая величина, имеющая независимый от выбора системы координат смысл. Это находит своё выражение, например, в том, что знание
J
iiв одной системе координат не позволяет найти
J
iiв другой системе координат. В то же время совокупность всех чисел
J
ijимеет смысл, независимый от выбора координатной системы. Знание всех чисел
J
ijв одной системе прямоугольных координат позволяет найти их в любой другой системе прямоугольных координат по формуле
Т. о., одной из основных задач Т. и. является нахождение аналитических формулировок законов механики, геометрии, физики, не зависящих от выбора координатной системы.
1. Тензоры в прямоугольных координатах.Величины, которые в каждой системе прямоугольных координат задаются в 3-мерном пространстве 3
kчислами
где
Примеры тензоров: если координаты вектора
аобозначить a
i
(
i =1, 2, 3), то числа
а, образуют тензор первой валентности. Любым двум векторам
а= {
a
i}
и
b={
b
i} соответствует тензор с компонентами
p
ij=
a
i. b
j.Этот тензор называется диадой. Если
a(
x
1, x
2, x
3)
-некоторое
,то каждой точке этого поля соответствует тензор с компонентами
2. Тензоры второй валентности.В приложениях Т. и. к механике, кроме тензоров первой валентности (векторов), чаще всего встречаются тензоры второй валентности. Если
p
ij=
p
ji,то тензор называется симметрическим, а если
p
ij= –p
ji,то - кососимметрическим (антисимметрическим). Симметрический тензор имеет шесть существенных компонент, а кососимметрический - три:
Тензор
Инвариантами тензора называются функции от его компонент, не зависящие от выбора координатной системы. Примером инварианта является след тензора
p
11+
p
22+
p
33.Так, для тензора инерции он равен удвоенному полярному моменту инерции относительно начала координат, для тензора
3. Тензоры в аффинных координатах.Для многих задач приходится рассматривать тензорные величины в аффинных координатах (косоугольных координатах с различными единицами длины по разным осям). Положение одной аффинной системы координат относительно другой может быть описано двумя различными системами чисел: числами
При рассмотрении прямоугольных координат не приходится различать ковариантные (нижние) и контравариантные (верхние) индексы тензора, так как для двух таких систем координат
Коэффициенты уравнения поверхности второго порядка
Дословно, так же как и в трёхмерном пространстве, определяются тензоры в n-мерном пространстве. Важным примером тензоров в n-мерном пространстве являются совокупности компонент . Порядок следования индексов существенным образом входит в определение тензора, то есть при перестановке индексов компоненты тензора, вообще говоря, меняются. Тензор называется симметрическим по данной совокупности индексов (одного и того же уровня), если при перестановке любых двух индексов этой совокупности он не меняется. Если же при такой перестановке компоненты тензора меняют знак, то он называется кососимметрическим по этой совокупности индексов. В более общем смысле условием симметрии тензора называют любую инвариантную линейную зависимость между его компонентами. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65 |
|||||||
 ,
, ).
). определяется выражением
i
аб= М(
R
1
Ч R
4
– R
2
Ч R
4)
,где
М -коэффициент пропорциональности,
R’
1и
R'
2
- сопротивления тензорезисторов, равные соответственно
R
1+ D
R
1(e) + D
R
1(q) и
R
2– D
R
2(e) + D
R
2(q). Мостовая цепь с двумя ТР позволяет повысить чувствительность Т. в 2 раза, а с четырьмя - в 4 раза по сравнению с мостовой цепью с одним ТР и обеспечивает полную термокомпенсацию.
определяется выражением
i
аб= М(
R
1
Ч R
4
– R
2
Ч R
4)
,где
М -коэффициент пропорциональности,
R’
1и
R'
2
- сопротивления тензорезисторов, равные соответственно
R
1+ D
R
1(e) + D
R
1(q) и
R
2– D
R
2(e) + D
R
2(q). Мостовая цепь с двумя ТР позволяет повысить чувствительность Т. в 2 раза, а с четырьмя - в 4 раза по сравнению с мостовой цепью с одним ТР и обеспечивает полную термокомпенсацию.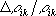 связана с
деформации
u
imчерез тензор четвёртого ранга
связана с
деформации
u
imчерез тензор четвёртого ранга
 :
:
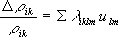 . На практике пользуются понятием тензочувствительности
. На практике пользуются понятием тензочувствительности
 , где
, где
 - относительное изменение длины
lобразца под действием приложенной нагрузки в определённом направлении,
- относительное изменение длины
lобразца под действием приложенной нагрузки в определённом направлении,
 - относительное изменение удельного электросопротивления r вдоль этого направления. В металлах
kпорядка единицы, в полупроводниках (например, в Ge и Si) в десятки и сотни раз больше.
- относительное изменение удельного электросопротивления r вдоль этого направления. В металлах
kпорядка единицы, в полупроводниках (например, в Ge и Si) в десятки и сотни раз больше.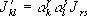 (
(
 и
и
 - некоторые числа): здесь, как принято в Т. и., опущен знак суммы и считается, что если один и тот же индекс встречается дважды (один раз наверху, а другой раз внизу), то по нему производится суммирование, причём этот индекс принимает все возможные для него значения (в приведённом примере - значения 1, 2, 3). Т. и., как и векторное исчисление, является математическим аппаратом, при котором исключается влияние выбора координатной системы. Это достигается тем, что задание компонент тензора в какой-либо системе координат определяет их во всех других системах координат. В Т. и. указываются методы получения соотношений между тензорами и функций от компонент тензоров, не меняющихся при переходе от одной системы координат к другой (инвариантных соотношений и инвариантов).
- некоторые числа): здесь, как принято в Т. и., опущен знак суммы и считается, что если один и тот же индекс встречается дважды (один раз наверху, а другой раз внизу), то по нему производится суммирование, причём этот индекс принимает все возможные для него значения (в приведённом примере - значения 1, 2, 3). Т. и., как и векторное исчисление, является математическим аппаратом, при котором исключается влияние выбора координатной системы. Это достигается тем, что задание компонент тензора в какой-либо системе координат определяет их во всех других системах координат. В Т. и. указываются методы получения соотношений между тензорами и функций от компонент тензоров, не меняющихся при переходе от одной системы координат к другой (инвариантных соотношений и инвариантов).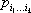 (
i
r= 1, 2, 3) и при замене системы координат (
x
1, x
2, x
3) системой (
x’
1, x’
2, x’
3) заменяются числами
(
i
r= 1, 2, 3) и при замене системы координат (
x
1, x
2, x
3) системой (
x’
1, x’
2, x’
3) заменяются числами
 по формулам:
по формулам: , (1)
, (1)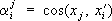 , называются тензорными величинами, а определяющие их системы чисел - тензорами в прямоугольных координатах (иногда тензорами называют также и сами тензорные величины). Число
kназывается валентностью (рангом) тензора, числа
, называются тензорными величинами, а определяющие их системы чисел - тензорами в прямоугольных координатах (иногда тензорами называют также и сами тензорные величины). Число
kназывается валентностью (рангом) тензора, числа
 - его компонентам и (координатами). Аналогичным образом определяются тензоры в пространстве любого числа измерений.
- его компонентам и (координатами). Аналогичным образом определяются тензоры в пространстве любого числа измерений. . Он называется производной вектора
а ={ai} по вектору
r{
x
1, x
2, хз} (обозначается также через
. Он называется производной вектора
а ={ai} по вектору
r{
x
1, x
2, хз} (обозначается также через
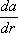 ). Упомянутая выше совокупность чисел
J
ijобразует тензор второй валентности (тензор инерции).
). Упомянутая выше совокупность чисел
J
ijобразует тензор второй валентности (тензор инерции). ;
;
 ;
;
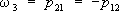
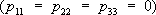 . При этом компоненты w
1, w
2, w
3преобразуются как компоненты псевдовектора (см.
)
.Вообще псевдовекторы (угловую скорость, векторное произведение двух векторов и др.) можно рассматривать как кососимметрические тензоры второй валентности. Далее, если в любой системе координат принять
. При этом компоненты w
1, w
2, w
3преобразуются как компоненты псевдовектора (см.
)
.Вообще псевдовекторы (угловую скорость, векторное произведение двух векторов и др.) можно рассматривать как кососимметрические тензоры второй валентности. Далее, если в любой системе координат принять
 ,
,
 ,
,
 , то получится тензор, называемый единичным тензором. Компоненты этого тензора обозначаются при помощи
d
ij.Тензоры инерции, напряжения, единичный тензор - симметрические. Всякий тензор единственным образом разлагается на сумму симметрических и кососимметрических тензоров. Если
а(
r) - вектор смещения частиц упругого тела при малой деформации, то симметрическая часть
, то получится тензор, называемый единичным тензором. Компоненты этого тензора обозначаются при помощи
d
ij.Тензоры инерции, напряжения, единичный тензор - симметрические. Всякий тензор единственным образом разлагается на сумму симметрических и кососимметрических тензоров. Если
а(
r) - вектор смещения частиц упругого тела при малой деформации, то симметрическая часть
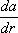 называется тензором деформации; кососимметрическая часть
называется тензором деформации; кососимметрическая часть
 соответствует псевдовектору
соответствует псевдовектору
 (см.
векторного поля).
(см.
векторного поля). является симметрическим только в том случае, когда поле
а(
r) потенциально (см.
)
.Разложение тензора
является симметрическим только в том случае, когда поле
а(
r) потенциально (см.
)
.Разложение тензора
 на симметрические и кососимметрические части соответствует разложению относительного смещения
daна чистую деформацию и на поворот тела как целого.
на симметрические и кососимметрические части соответствует разложению относительного смещения
daна чистую деформацию и на поворот тела как целого. -
векторного поля
a(
r) и т. д
-
векторного поля
a(
r) и т. д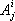 равными компонентам векторов
равными компонентам векторов
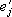 . нового базиса относительно векторов
. нового базиса относительно векторов
 старого базиса, и числами
старого базиса, и числами
 ,равными компонентам векторов
,равными компонентам векторов
 относительно базиса
относительно базиса
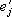 . В соответствии с этим бывают тензоры различного вида: в законы преобразования одних из них входят числа
. В соответствии с этим бывают тензоры различного вида: в законы преобразования одних из них входят числа
 ,а в законы преобразования других - числа
,а в законы преобразования других - числа
 .Встречаются и тензоры, в законы преобразования которых входят как числа
.Встречаются и тензоры, в законы преобразования которых входят как числа
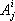 , так и числа
, так и числа
 .Тензоры первого вида называются ковариантными, второго - контравариантными и третьего - смешанными тензорами. Более точно, (
r+
х)-валентным смешанным тензором
sраз ковариантным и
rраз контравариантным. называют совокупность 3
r+s
чисел
.Тензоры первого вида называются ковариантными, второго - контравариантными и третьего - смешанными тензорами. Более точно, (
r+
х)-валентным смешанным тензором
sраз ковариантным и
rраз контравариантным. называют совокупность 3
r+s
чисел
 , заданную в каждой системе аффинных координат и преобразующуюся при переходе от одной системы координат к другой по формулам:
, заданную в каждой системе аффинных координат и преобразующуюся при переходе от одной системы координат к другой по формулам: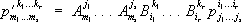
 .
. образуют ковариантный тензор валентности 2, а элементы
образуют ковариантный тензор валентности 2, а элементы
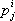 матрицы линейного преобразования - тензор, 1 раз ковариантный и 1 раз контравариантный. Система трёх чисел
x
1,
x
2, x
3,преобразующихся как координаты вектора
x = x
ie
i,образует 1 раз контравариантный тензор, а система чисел, преобразующихся как скалярное произведение
x
i= xe
i,образует 1 раз ковариантный тензор. Относительно преобразования аффинных координат символ Кронекера
матрицы линейного преобразования - тензор, 1 раз ковариантный и 1 раз контравариантный. Система трёх чисел
x
1,
x
2, x
3,преобразующихся как координаты вектора
x = x
ie
i,образует 1 раз контравариантный тензор, а система чисел, преобразующихся как скалярное произведение
x
i= xe
i,образует 1 раз ковариантный тензор. Относительно преобразования аффинных координат символ Кронекера
 является смешанным тензором (поэтому, в отличие от пункта 2, здесь пишут один индекс сверху, другой - снизу). Совокупность чисел
g
ij= e
ie
j,где
e
i- векторы базиса, образует тензор, называемый ковариантным метрическим тензором. Длина любого вектора пространства
х = xieiравна
является смешанным тензором (поэтому, в отличие от пункта 2, здесь пишут один индекс сверху, другой - снизу). Совокупность чисел
g
ij= e
ie
j,где
e
i- векторы базиса, образует тензор, называемый ковариантным метрическим тензором. Длина любого вектора пространства
х = xieiравна
 , а скалярное произведение двух векторов
хи
уравно
g
ijx
iy
j.Совокупность величин
g
ijтаких, что
, а скалярное произведение двух векторов
хи
уравно
g
ijx
iy
j.Совокупность величин
g
ijтаких, что
 , образует тензор, который называется контравариантным метрическим тензором.
, образует тензор, который называется контравариантным метрическим тензором.