 |
|
���������� ������:: ������ ����� ���� :: ���� ��������� :: ����� ����� �������� :: ������� ������ :: ������ ����� :: ��� :: ������� ��� ���������� :: �������� ����� :: ������ ������� �������� :: ������ ���� ���������� �����:: The Boarding House :: ���� (����� 1-3) :: ���� :: ���� ������ ������ :: ��� � ��� :: ����� �������� � ������ :: ������������ ���� ��� ������ :: ���������� ���-�������� :: ���� �����-������ :: ���������� ����� � ������ |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 32)
Лит.:Айзенберг Г. З., Антенны ультракоротких воля, [ч. 1], М., 1957; Лавров Г. А., Князев А. С., Приземные и подземные антенны, М., 1965; Драбкин А. Л., 3узенко В. Л., Кислов А. Г., Антенно-фидерные устройства, 2 изд., М., 1974. Г. А. Клигер, В. И. Комиссаров. 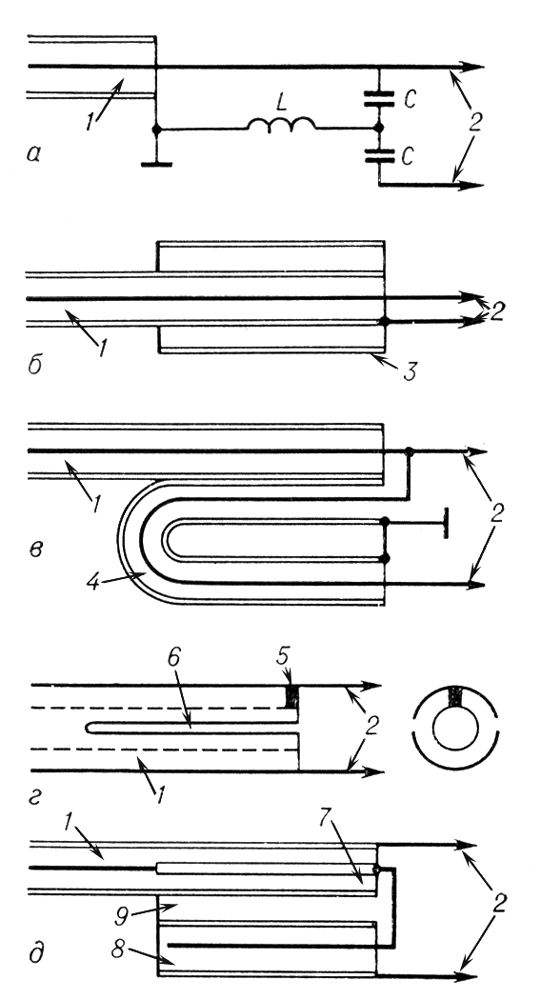
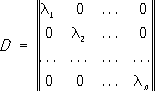
Симметрирующие устройства: а - однозвенное; б - «четвертьволновой стакан»; в - «U-колено»; г - коаксиально-щелевой переход; д - устройство с компенсацией рассогласования; 1 - несимметричная линия; 2 - симметричная линия; 3 - «стакан»; 4 - полуволновая петля; 5 - проводящая перемычка; 6 - щель; 7 - коаксиальный трансформатор; 8 - компенсирующий разомкнутый шлейф; 9 - симметрирующий короткозамкнутый шлейф; L - катушка индуктивности; С - конденсатор. Симметрическая группа Симметри'ческая гру'ппаn-й степени, группа , состоящая из всех перестановок nобъектов. В С. г. n! элементов. Перестановки С. г. с чётным числом инверсии образуют знакопеременную, или полусимметрическую, подгруппу С. г., имеющую n!/2 элементов. Симметрическая матрица Симметри'ческая ма'трица,квадратная матрица S= ll s ikll, в которой любые два элемента, симметрично расположенные относительно главной диагонали, равны между собой: s ik= s ki( i, k =1,2,..., n). С. м. часто рассматривается как матрица коэффициентов некоторой квадратичной формы ; между теорией С. м. и теорией квадратичных форм существует тесная связь. Спектральные свойства С. м. с действительными элементами: 1) все корни l 1, l 2,..., l n характеристического уравнения С. м. действительны; 2) этим корням соответствуют nпопарно ортогональных собственных векторов С. м. ( n- порядок С. м.). С. м. с действительными элементами всегда представима в виде: S'= ODO -1 где О ортогональная матрица , а
Симметрические функции
Симметри'ческие фу'нкции,функции нескольких переменных, не изменяющиеся при любых перестановках переменных, например
где суммы распространены на комбинации неравных между собой чисел k, l,...; они имеют первую степень относительно каждого из переменных. Согласно формулам Виета, x 1, x 2,..., x nявляются корнями уравнения: x n- f 1x n-1+ f 2x n-2-··· +(- 1) nf n= 0. Согласно основной теореме теории С. ф., любой с. м. представляется как многочлен от э. с. м., и притом только единственным образом: F( x 1, x 2., ..., x n) = G( f 1, f 2,..., f n); если все коэффициенты в Fцелые, то и коэффициенты в G целые. Иными словами, всякий с. м. от корней уравнения выражается целым рациональным образом через его коэффициенты; например,
Другим важным классом С. ф. являются степенные суммы
Они связаны с э. с. м. формулами Ньютона
s
i- f
1s
l-1+ f
2s
l-2+ ··· + (- 1)
l
f
l= 0,
и s n+l- f 1s n+l-1+ ··· +(-1) n f ns l=0,
позволяющими последовательно выражать f kчерез s rnи обратно. Функция называется кососимметрической, или знакопеременной, если она не изменяется при чётных перестановках x 1, x 2, ..., x nи меняет знак при нечётных перестановках. Такие функции рационально выражаются через f 1, f 2, ..., f nи разностное произведение (см. Дискриминант ) D = П к<1( x k- x l), квадрат которого является С. ф. и потому рационально выражается через f 1, f 2,..., f n.
Лит.:Курош А. Г., Курс высшей алгебры, 10 изд., М., 1971. Симметричность Симметри'чностьв математике и логике, свойство бинарных (двуместных, двучленных) отношений , выражающее независимость выполнимости данного отношения для какой-либо пары объектов от порядка, в котором эти объекты входят в пару: отношение Rназывается симметричным, если для любых объектов xи yиз области определения xRyвлечёт yRx. Примерами симметричных отношений служат отношения типа равенства ( тождества , эквивалентности , подобия ), их «ослабленные формы» - отношения толерантности (сходства, соседства и т. п.), а также (как следует из данного выше определения) обратные к ним отношения неравенства и др. Отношение Rназывается антисимметричным, если из xRyпри х( уследует щ yRx(отрицание yRx), т. е. если из xRyи yRxнепременно следует х = у, таковы, например, отношения порядка (по величине или какому-либо другому упорядочивающему критерию) между числами или другими объектами, отношение включения между множествами и т. п. В применении к логическим и логико-математическим операциям свойство С. называется коммутативностью (перестановочностью); например, результаты сложения и умножения чисел, объединения и пересечения множеств, дизъюнкция и конъюнкция высказываний (см. Алгебра логики ) не зависят от порядка слагаемых, сомножителей и т. д. Понятия С. и коммутативности естественно обобщаются на случай произвольного числа объектов. Симметрия (в биологии) Симметри'яв биологии (биосимметрия). На явление С. в живой природе обратили внимание ещё в Древней Греции пифагорейцы (5 в. до н. э.) в связи с развитием ими учения о гармонии. В 19 в. появились единичные работы, посвященные С. растений (французские учёные О. П. Декандоль, О. Браво), животных (немецкий - Э. Геккель), биогенных молекул (французские - А. Вешан, Л. Пастер и др.). В 20 в. биообъекты изучали с позиций общей теории С. (советские учёные Ю. В. Вульф, В. Н. Беклемишев, Б. К. Вайнштейн, голландский физикохимик Ф. М. Егер, английский кристаллографы во главе с Дж. Берналом) и учения о правизне и левизне (советские учёные В. И. Вернадский, В. В. Алпатов, Г. Ф. Гаузе и др.; немецкий учёный В. Людвиг). Эти работы привели к выделению в 1961 особого направления в учении о С. - биосимметрики. Наиболее интенсивно изучалась структурная С. биообъектов. Исследование С. биоструктур - молекулярных и надмолекулярных - с позиций структурной С. позволяет заранее выявить возможные для них виды С., а тем самым число и вид возможных модификаций, строго описывать внешнюю форму и внутреннее строение любых пространственных биообъектов. Это привело к широкому использованию представлений структурной С. в зоологии, ботанике, молекулярной биологии. Структурная С. проявляется прежде всего в виде того или иного закономерного повторения. В классической теории структурной С., развитой немецким учёным И. Ф. Гесселем, Е. С. Федоровым и другими, вид С. объекта может быть описан совокупностью элементов его С., т. е. таких геометрических элементов (точек, линий, плоскостей), относительно которых упорядочены одинаковые части объекта (см. Симметрия в математике). Например, вид С. цветка флокса ( рис. 1 , в) - одна ось 5-го порядка, проходящая через центр цветка; производимые посредством её операции - 5 поворотов (на 72, 144, 216, 288 и 360°), при каждом из которых цветок совпадает с самим собой. Вид С. фигуры бабочки ( рис. 2 , б) - одна плоскость, делящая её на 2 половины - левую и правую; производимая посредством плоскости операция - зеркальное отражение, «делающее» левую половинку правой, правую - левой, а фигуру бабочки совмещающей с самой собой. Вид С. радиолярии Lithocubus geometricus ( рис. 3 , б), помимо осей вращения и плоскостей отражения содержит ещё и центр С. Любая проведённая через такую единственную точку внутри радиолярии прямая по обе стороны от неё и на равных расстояниях встречает одинаковые (соответственные) точки фигуры. Операции, производимые посредством центра С., - отражения в точке, после которых фигура радиолярии также совмещается сама с собой. В живой природе (как и в неживой) из-за различных ограничений обычно встречается значительно меньшее число видов С., чем возможно теоретически. Например, на низших этапах развития живой природы встречаются представители всех классов точечной С. - вплоть до организмов, характеризующихся С. правильных многогранников и шара (см. рис. 3 ). Однако на более высоких ступенях эволюции встречаются растения и животные в основном т. н. аксиальной (вида n) и актиноморфной (вида n( m) С. (в обоих случаях nможет принимать значения от 1 до Ґ). Биообъекты с аксиальной С. (см. рис. 1 ) характеризуются лишь осью С. порядка n. Биообъекты сактиноморфной С. (см. рис. 2 ) характеризуются одной осью порядка nи пересекающимися по этой оси плоскостями m. В живой природе наиболее распространены С. вида n =1 и 1Ч m = m, называется соответственно асимметрией и двусторонней, или билатеральной, С. Асимметрия характерна для листьев большинства видов растений, двусторонняя С. - до известной степени для внешней формы тела человека, позвоночных животных и многих беспозвоночных. У подвижных организмов такая С., по-видимому, связана с различиями их движении вверх-вниз и вперёд-назад, тогда как их движения направо-налево одинаковы. Нарушение у них билатеральной С. неизбежно привело бы к торможению движения одной из сторон и превращению поступательного движения в круговое. В 50-70-х гг. 20 в. интенсивному изучению (прежде всего в СССР) подверглись т. н. диссимметрические биообъекты ( рис. 4 ). Последние могут существовать по крайней мере в двух модификациях - в форме оригинала и его зеркального отражения (антипода). При этом одна из этих форм (неважно какая) называется правой или D (от лат. dextro), другая - левой или L (от лат. laevo). При изучении формы и строения D- и L-биообъектов была развита теория диссимметризующих факторов, доказывающая возможность для любого D- или L-объекта двух и более (до бесконечного числа) модификаций (см. также рис. 5 ); одновременно в ней содержались и формулы для определения числа и вида последних. Эта теория привела к открытию т. н. биологической изомерии (разных биообъектов одного состава; на рис. 5 изображены 16 изомеров листа липы). При изучении встречаемости биообъектов было установлено, что в одних случаях преобладают D-, в других L-формы, в третьих они представлены одинаково часто. Бешаном и Пастером (40-е гг. 19 в.), а в 30-х гг. 20 в. советским учёным Г. Ф. Гаузе и другими было показано, что клетки организмов построены только или преимущественно из L-amинокислот, L-белков, D-дезоксирибонуклеиновых кислот, D-сахаров, L-алкалоидов, D- и L-терпенов и т. д. Столь фундаментальная и характерная черта живых клеток, названная Пастером диссимметрией протоплазмы, обеспечивает клетке, как было установлено в 20 в., более активный обмен веществ и поддерживается посредством сложных биологических и физико-химических механизмов, возникших в процессе эволюции. Сов. учёный В. В. Алпатов в 1952 на 204 видах сосудистых растений установил, что 93,2% видов растений относятся к типу с L-, 1,5% - с D-ходом винтообразных утолщений стенок сосудов, 5,3% видов - к типу рацемическому (число D-сосудов примерно равно числу L-сосудов). При изучении D- и L-биообъектов было установлено, что равноправие между D-и L-формами в ряде случаев нарушено из-за различия их физиологических, биохимических и др. свойств. Подобная особенность живой природы была названа диссимметрией жизни. Так, возбуждающее влияние L-amинокислот на движение плазмы в растительных клетках в десятки и сотни раз превосходит такое же действие их D-форм. Многие антибиотики (пенициллин, грамицидин и др.), содержащие D-amинокислоты, обладают большей бактерицидностью, чем их формы c L-amинокислотами. Чаще встречающиеся винтообразные L-kopнеплоды сахарной свёклы на 8-44% (в зависимости от сорта) тяжелее и содержат на 0,5-1% больше сахара, чем D-kopнеплоды. Изучение наследования признаков у D- и L-форм показало, что их правизна или левизна может быть наследственной, ненаследственной или имеет характер длительной модификации . Это означает, что по крайней мере в ряде случаев правизну-левизну организмов и их частей можно изменить действием мутагенных или немутагенных химических соединений. В частности, D-штаммы (по морфологии колоний) микроорганизма Bacillus mycoides при выращивании их на агаре с D-сахарозой, L-днгитонином, D-винной кислотой можно превратить в L-штаммы, а L-штаммы можно превратить в D-штаммы, выращивая их на агаре с L-винной кислотой и D-аминокислотами. В природе взаимопревращения D- и L-форм могут происходить и без вмешательства человека. При этом смена видов С. в эволюции происходила не только у диссимметрических организмов. В результате возникли многочисленные эволюционные ряды С., специфичные для тех или иных ветвей древа жизни. Структурная С. биосистем изучается также с точки зрения более общих типов С. - цветной С., С. подобия, антисимметрии и др. Разработка учения о С. биообъектов позволит углубить представления как об их свойствах и функциях, так и о происхождении и сущности жизни . Лит.:Гаузе Г. Ф., Асимметрия протоплазмы, М. - Л., 1940; Вайнштейн Б. К., Дифракция рентгеновых лучей на цепных молекулах, М., 1963; Беклемишев В. Н., Основы сравнительной анатомии беспозвоночных, 3 изд., т. 1-2, М., 1964; Урманцев Ю. А., Симметрия природы и природа симметрии, М., 1974; Ludwig W., Das Rechts-Links-Problem im Tierreich und beim Menschen..., B. - Hdib. - N. Y., 1970; Bentley R., Molecular asymmetry in biology, v. 1-2, N. Y., 1969-70. Ю. А. Урманцев. 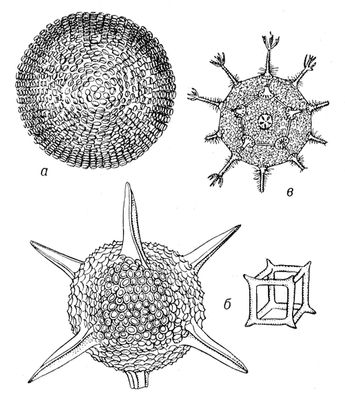
Рис. 3. Биообъекты с совершенной точечной симметрией. Радиолярии: а - шарообразная Ethmosphaera polysyphonia, содержащая бесконечное число осей бесконечного порядка + бесконечное число плоскостей симметрии + центр симметрии; б - кубические Hexastylus marginatus и Lithocubus geometricus, характеризующиеся симметрией куба; в - додекаэдрическая Circorhegma dodecahedra, характеризующаяся симметрией правильных многогранников - додекаэдра и икосаэдра. 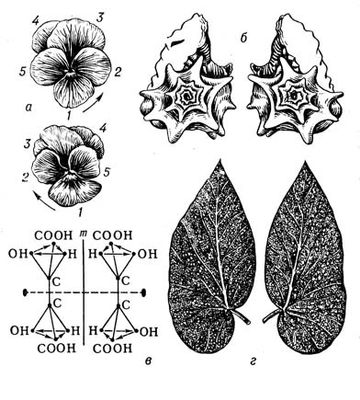
Рис. 4. Диссимметрические D- и L-биообъекты: а - цветки анютиных глазок; б - раковины прудовика; в - молекулы винной кислоты; г - листья бегонии. 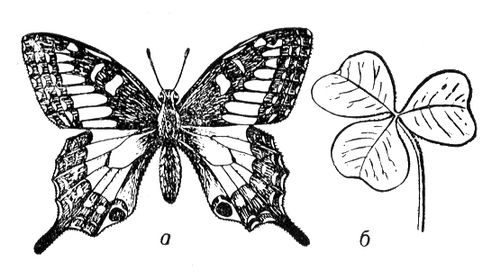
Рис. 2. Актиноморфная симметрия; а - бабочка; б - лист кислицы; симметрии соответственно 1Чm, 3Чm. Бабочке свойственна двусторонняя, или билатеральная, симметрия. 
Рис. 5. Лист липы, иллюстрирующий возможность существования диссимметрических объектов более чем в двух (в данном случае в 16) модификациях. Для листа липы диссфакторы - это 4 морфологических признака: преимущественные ширина (ш) и длина (д), асимметричные жилкование (ж) и загиб главной жилки (г). Так как каждый из диссфакторов может проявляться двояко - в (+)- или ( - )-формах - и соответственно приводить к D- или L-мoдификациям, то число возможных модификаций будет 2 4= 16, а не две. 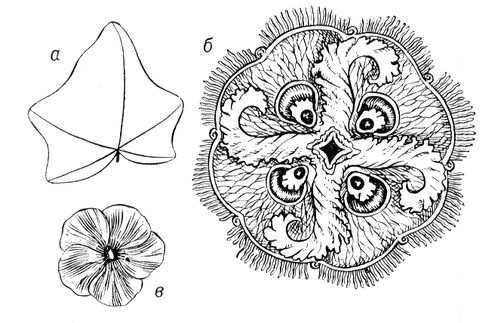
Рис. 1. Аксиальная симметрия: а - лист плюща; б - медуза Aurelia insulinda; в - цветок флокса. При повороте этих фигур вокруг оси симметрии равные части каждого из них совпадут друг с другом соответственно 1, 4, 5 раз (оси 1, 4, 5-го порядка). Лист плюща асимметричен. 
Рис. 3д. Биообъекты с совершенной точечной симметрией. Радиолярии: модель аденовируса в форме икосаэдра. 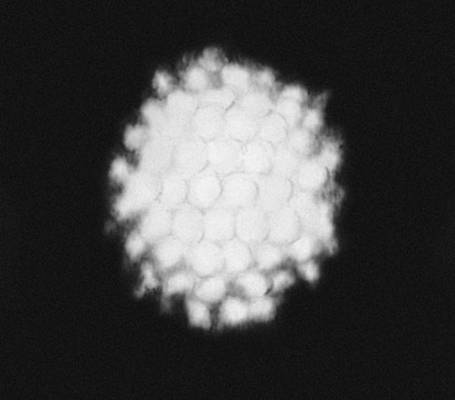
Рис. 3г. Биообъекты с совершенной точечной симметрией. Радиолярии: частица аденовируса в форме икосаэдра. Симметрия (в математике) Симме'трия(от греч. symmetria - соразмерность) в математике, 1) симметрия (в узком смысле), 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82 |
|||||||
 .
.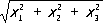 или
или
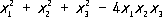 . Особое значение в алгебре имеют симметрические многочлены (с. м.) и среди них - элементарные симметрические многочлены (э. с. м.) - функции
. Особое значение в алгебре имеют симметрические многочлены (с. м.) и среди них - элементарные симметрические многочлены (э. с. м.) - функции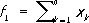 ,
,
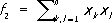 ,
,
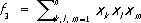 , …,
, …,
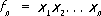 ,
,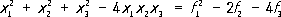 .
.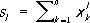 .
.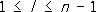 ,
,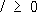 ,
,