 |
|
���������� ������:: ������ ����� ���� :: ���� ��������� :: ����� ����� �������� :: ������� ������ :: ������ ����� :: ��� :: ������� ��� ���������� :: �������� ����� :: ������ ������� �������� :: ������ ���� ���������� �����:: The Boarding House :: ���� (����� 1-3) :: ���� :: ���� ������ ������ :: ��� � ��� :: ����� �������� � ������ :: ������������ ���� ��� ������ :: ���������� ���-�������� :: ���� �����-������ :: ���������� ����� � ������ |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 26)
Унитарная симметрия SU (3).Открытие большого числа резонансов и установление их квантовых чисел показало, что адроны, входящие в разные изотопические мультиплеты, могут быть объединены в более широкие группы частиц с одинаковыми спинами, чётностью и барионным зарядом, но с разными гиперзарядами - т. н. супермультиплеты. Например, 8 барионов со спином 1/ 2и положит. чётностью: нуклоны N (протон и нейтрон) с изотопическим спином I= 1/ 2и гиперзарядом Y= 1, S-гипероны (S +,S 0,S -) c I= 1, Y= 0, L-гиперон с I= 0, Y= 0, X-гипероны (X 0, X -) с I= 1/ 2, Y= - 1 могут быть объединены в единый супермультиплет - октет барионов. В супермультиплет (декаплет) объединяются также барионы со спином 3/ 2и положительной чётностью; этот мультиплет включает резонансы D (D ++, D +, D 0, D -) с I= 3/ 2, Y= 1, резонансы S* (S +*, S 0*, S -*) c l= 1, Y= 0, резонансы X* (X 0*, X -*) с I= 1/ 2, Y= - 1 и W -= гиперон с I= 0, Y= - 2. Аналогичным образом в супермультиплеты объединяются и мезоны. Например, p-мезоны (p +, p 0, p -) с I= 1, Y= 0, K-мезоны (K +, K 0, K -, K 0) с I= 1/ 2, Y= ± 1 и h-мезон c I= 0, Y= 0 объединяются в октет мезонов со спином 0 и отрицательной чётностью. Поскольку, однако, массы частиц, входящих в один и тот же супермультиплет, заметно отличаются друг от друга, ясно, что симметрия С. в., вследствие которой существуют группы «похожих» частиц, является не точной, а приближенной симметрией. Можно считать, что С. в. складывается из обладающего высокой степенью симметрии т. н. «сверхсильного» взаимодействия и нарушающего симметрию «умеренно сильного» взаимодействия. Сверхсильное взаимодействие не зависит ни от электрического заряда, ни от гиперзаряда частиц. При наличии одного только сверхсильного взаимодействия массы всех частиц внутри одного супермультиплета должны были бы быть одинаковыми. Наблюдаемое в действительности различие масс частиц с разными гиперзарядами происходит из-за существования умеренно сильного взаимодействия, которое зависит определенным образом от гиперзаряда и изотопического спина. Состав обнаруженных на опыте супермультиплетов, т. е. число частиц и их квантовые числа, можно объяснить, если считать, что сверхсильное взаимодействие инвариантно относительно преобразований группы SU(3), включающих в себя в качестве подгруппы изотопическое преобразование SU(2). Для объяснения наблюдаемой на опыте SU(3)-симметрии С. в. выдвинута гипотеза, согласно которой адроны состоят из трёх типов фундаментальные частиц - кварков p, n, l, а С. в. не меняется при замене волновой функции каждой из этих частиц на суперпозицию всех остальных [аналогично тому, как это имеет место для преобразования (1)]. Поскольку указанное преобразование осуществляется с помощью унитарных матриц 3-го порядка с детерминантом 1, инвариантность С. в. относительно него и означает существование SU(3)-симметрии. Предполагая далее, что масса странного l-кварка больше массы p-, n-kварков, можно удовлетворит. образом объяснить и наблюдаемое нарушение SU(3)-симметрии (выражающееся в различии масс частиц с разными гиперзарядами и изотопическими спинами в одном и том же супермультиплете). Гипотеза о существовании кварков, выдвинутая для объяснения наблюдаемого состава супермультиплетов адронов, позволяет объяснить также ряд динамических закономерностей С. в. Существуют различные обобщения первоначальной гипотезы кварков. Высказываются также соображения, согласно которым кварки могут существовать только в связанных состояниях и не должны наблюдаться как свободные частицы. Основные направления развития теории сильных взаимодействий Поскольку для описания процессов С. в. теория возмущений (столь эффективная в квантовой электродинамике) неприменима, основные направления современной теории С. в. связаны с использованием общих принципов квантовой теории поля, симметрии С. в. и различных модельных представлений, в той или иной степени учитывающих многочастичный характер взаимодействия. В наиболее общем виде процессы, происходящие при взаимодействии частиц, могут быть описаны с помощью матрицы рассеяния ( S-maтрицы), связывающей состояние системы до реакции с состоянием системы после реакции (В. Гейзенберг , 1943). Элементы матрицы рассеяния представляют амплитуды перехода из различных начальных в различные конечные состояния системы. Т. о., задание матрицы рассеяния полностью определяет вероятности различных каналов реакций при взаимодействии частиц. Общие принципы квантовой теории поля позволяют получить соотношения, связывающие характеристики различных процессов С. в., и установить определенные ограничения на характер процессов С. в. при высоких энергиях. Эти соотношения являются основой для построения различных приближенных моделей, описывающих экспериментально наблюдаемые закономерности процессов С. в. Один из основных принципов квантовой теории поля - унитарность матрицы рассеяния, заключающаяся в том, что сумма вероятностей всех возможных переходов, которые могут происходить в какой-либо системе, должна быть равна единице (при этом, естественно, предполагается, что совокупность возможных состояний системы является полной). Из условия унитарности вытекает, в частности, т. н. оптическая теорема, согласно которой полное эффективное сечение рассеяния частиц связано с мнимой частью амплитуды упругого рассеяния частиц на нулевой угол. Условие унитарности ограничивает также величину сечения для отдельных парциальных волн, т. е. волн с определенным орбитальным (угловым) моментом количества движения (см. Рассеяние микрочастиц ). Далее, выполнение законов специальной теории относительности (
релятивистская инвариантность
, или лоренц-инвариантность) даёт возможность сформулировать принцип микропричинности для элементарных процессов С. в. (см.
Микропричинности условие
). Согласно специальной теории относительности, два события, разделённые пространственно-подобным интервалом, не могут быть причинно-связанными (т. к. расстояние между событиями в этом случае больше, чем путь, который может быть пройден любым сигналом за интервал времени между событиями). Если же события разделены времениподобным интервалом, то только события, предшествующие по времени данному событию, могут явиться его причиной. Такая общая форма принципа микропричинности накладывает определённые ограничения на аналитическую структуру функций, описывающих причинно-связанные события. Это было замечено ещё в классической электродинамике сплошных сред при описании зависимости
диэлектрической проницаемости
e вещества (а следовательно, и показателя преломления волн) от частоты w электромагнитного поля, e (w) (т. н. дисперсия). Для переменных полей значение электрической индукции
D(
t) в некоторый момент времени
tопределяется значениями напряжённости электрического поля
Ев предшествующие моменты времени
t'(согласно принципу причинности,
В этом выражении f( t- t’) - функция, которая определяется внутренним строением диэлектрика. Её конкретное выражение для дальнейших выводов несущественно; важно лишь, что в силу трансляционной инвариантности по времени, т. е. независимости от выбора начала отсчёта времени, функция f( t- t') зависит только от разности времён ( t- t'). При этом в соответствии с принципом причинности интегрирование по t'ведётся до момента t. Для компонент Фурье (см. Фурье интеграл ) D(w) и Е(w) величин D( t) и E( t) будет иметь место соотношение: D(w) = e (w) Е(w), (3), где диэлектрическая проницаемость e (w) представляет собой комплексную функцию и равна:
пределы интегрирования t ³ 0 вытекают из условия причинности. Соотношение (4), определённое для действительных значений w, может быть продолжено в область комплексных значений переменного аргумента со. Если положить w = w’ +
iw’’, где w’ и w’’ - действительные числа, определяющие соответственно действительную и мнимую части w, то в интеграле выражения (4) возникает множитель
е
-
w
''
t, обеспечивающий сходимость интеграла при (w’’ > 0,
где символ Розначает т. н. главное значение интеграла, т. е. исключающее особую точку w '= w. Существенно, что реальная и мнимая части e(w) могут быть непосредственно измерены на опыте [Im e(w) связана с поглощением электромагнитных волн]. Установление аналитических свойств амплитуды рассеяния частиц представляет значительно более сложную задачу. Основополагающие работы в этом направлении были сделаны Н. Н. Боголюбовым на основе сформулированного им для метода S-мaтрицы принципа микропричинности. Рассмотрим реакцию упругого рассеяния, в результате которой две частицы «а» и «b» с начальными четырёхмерными импульсами p aи p bпереходят в состояние с четырёхмерными импульсами соответственно р’ аи p' b[четырёхмерный импульс частицы включает энергию частицы Еи её пространств, импульс р, а квадрат четырёхмерного импульса ( p 2) в единицах измерения, в которых скорость света с= 1, определяется как p 2= Е 2– p 2 и равен квадрату массы частицы: p 2= M 2]. Закон сохранения энергии и импульса в реакции рассеяния может быть записан в виде равенства p a+ p b= p' a+ р’ b. Наиболее просто упругое рассеяние частиц выглядит в с. ц. и. сталкивающихся частиц. В этой системе p a+ p b= p' a+ p’ b= 0, т. е. импульсы частиц после столкновения направлены в противоположные стороны и равны по абсолютной величине начальным импульсам: | p a| = | p b| = | p’ a| = | р’ b| (см. рис. 2 ). Амплитуда рассеяния является функцией двух переменных: энергии системы Еи угла J, на который в результате рассеяния отклоняется одна из частиц. Эти переменные могут быть выражены через 2 независимые релятивистски инвариантные величины s = ( p a+ p b) 2= ( p’ a+ p’ b) 2, t = ( p’ a– p a) 2= ( p’ b– p b) 2. В с. ц. и. величина sравна квадрату полной энергии системы: s= ( E a+ E b) 2, а величина tравна (с обратным знаком) квадрату переданного (трёхмерного) импульса, t= – ( p’ a– p a) 2, и выражается через угол рассеяния J: t= – 2 p 2(1 – cosJ), где р- импульс частиц в с. ц. и. Наряду с величинами s, tвводится третья релятивистски инвариантная величина и. u= ( р’ b– p a) 2= ( р’ b– p b) 2, (6’) которая в силу закона сохранения энергии-импульса связана с величинами sи t соотношением: s+ t+ u= 2 m a+ 2 m b, где ma, m b- массы частиц «а» и «b». В процессах упругого рассеяния частиц область изменения величины sограничена неравенством s³ ( m a+ m b), а область изменения t- неравенствами 0 > t> -4 p 2. Эту область изменения переменных называется физической областью. Амплитуда рассеяния при фиксированной передаче импульса tможет быть продолжена в комплексную область по энергетической переменной sи оказывается связанной с амплитудой рассеяния античастиц . Эта связь заключается в следующем. Рассмотрим наряду с реакцией упругого рассеяния какого-либо частиц, например p ±-мезонов на протонах: p +( p) + р( q) ® p +( p') + р( q') (I) (в скобках указаны четырёхмерные импульсы частиц), реакцию рассеяния p -(- р) + р( q) ® p -(- p’) + р( q), (II) получающуюся из (1) переносом символа p-мезона из одной части равенства в другую с одновременной заменой частицы (p +) на античастицу (p -) и знаков их четырёхмерных импульсов: р® - р, p'® - p'. При переходе от процесса (I) к процессу (II) переменная tостаётся неизменной, а sи именяются местами. Физической области обоих процессов соответствуют двум различным неперекрывающимся областям изменения кинематических переменных s, и. Доказательство Боголюбовым аналитичности амплитуды в комплексной плоскости переменной sпозволяет утверждать, что амплитуды процессов I и II являются предельными значениями единой аналитической функции Ft( s) в разных областях изменения переменной sс разрезами на вещественной оси ( рис. 4 ). Правый разрез определяется условием s³ ( М+ m)' (где Ми m, - массы протона и пиона), а левый разрез - условием u= 2 M 2+ 2m 2- s- t³ ( M+ m 2). На «верхнем берегу» правого разреза Ft( s) совпадает с амплитудой T( s, t) процесса (I):
а на «нижнем берегу» левого разреза - с амплитудой процесса (II):
Отсюда вытекает соотношение т. н. перекрёстной симметрии (или кроссинг-симметрии):
Это соотношение связывает значение амплитуды одного процесса в его физической области со значением амплитуды др. процесса вне физической области последнего. Поэтому соотношение перекрёстной симметрии не имело бы смысла, если бы не существовало продолжения амплитуды процесса (1) из его физической области на левый разрез. Для определения особых точек аналитической функции Ft( s) важнейшее значение имеет продолжение условия унитарности S-maтрицы в «нефизическую» область кинематических переменных (лежащую вне «физических» областей, определяемых законами сохранения энергии и импульса для начальных и конечных состояний). Так, если две частицы «а» и «b» могут переходить в результате С. в. в виртуальную частицу «с»: а + b ® с, то из условия унитарности следует, что амплитуда процесса рассеяния а + b ® а + b будет иметь полюс по переменной sпри значении s= mc2, где mc- масса частицы «с». Этот полюс при mc< ma+ m bлежит в «нефизической» области процесса упругого рассеяния а + b ® а + b [«физическая» область, как уже отмечалось, начинается с s= ( m a+ m b) 2]. Если же mc> ma+ m b, частица «с» нестабильна относительно распада (за счёт С. в.) с ® а + b, т. е. является резонансом, и полюс амплитуды расположен на «нефизическом» листе римановой поверхности, соответствующем аналитическому продолжению амплитуды через разрез в комплексной плоскости s(см. Аналитические функции ). Тот факт, что особенности амплитуды, связанные с образованием виртуальных частиц, лежат в «нефизической» области, имеет простой смысл. Действительно, рождение виртуальных частиц сопровождается нарушением закона сохранения энергии, происходящим на короткое время в соответствии с соотношением неопределённостей. Поскольку физические области определяются законами сохранения энергии-импульса и условием стабильности начальных и конечных частиц в процессах С. в., образованию виртуальных состояний соответствуют значения кинематических переменных, лежащие вне этих областей. Т. о., именно в «нефизических» областях кинематических переменных содержится информация о процессах обмена виртуальными частицами, посредством которого и осуществляется С. в. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82 |
|||||||
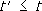 ). Поэтому общая линейная связь этих величин может быть записана:
). Поэтому общая линейная связь этих величин может быть записана: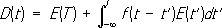 . (2)
. (2)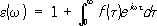 ; (4)
; (4)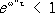 . Т. о., из условия причинности следует, что функция e(w) является
аналитической функцией
в верхней полуплоскости комплексного переменного со (w’’ > 0). Переход в «нефизическую» область комплексных значений со имеет глубокий смысл, т. к. для аналитических функций справедлива
Коши теорема
, позволяющая выразить значение функции для какого-либо значения переменного через интеграл Коши от этой функции. Выбирая действительное значение переменного, можно получить соотношения для реально измеряемых физических величин. Так были получены дисперсионные соотношения, позволяющие выразить, например, действительная часть (Re) диэлектрической проницаемости через интеграл от её мнимой части (Im):
. Т. о., из условия причинности следует, что функция e(w) является
аналитической функцией
в верхней полуплоскости комплексного переменного со (w’’ > 0). Переход в «нефизическую» область комплексных значений со имеет глубокий смысл, т. к. для аналитических функций справедлива
Коши теорема
, позволяющая выразить значение функции для какого-либо значения переменного через интеграл Коши от этой функции. Выбирая действительное значение переменного, можно получить соотношения для реально измеряемых физических величин. Так были получены дисперсионные соотношения, позволяющие выразить, например, действительная часть (Re) диэлектрической проницаемости через интеграл от её мнимой части (Im):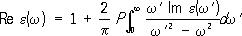 , (5)
, (5)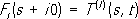 ,
,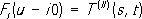 .
.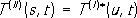 .
.