Большая Советская Энциклопедия (СХ)
Схалкер Корнелис
Сха'лкер(Schalker) Корнелис (31.7. 1890, — 13.1.1944, Схевенинген, близ Гааги), деятель нидерландского рабочего движения. В 1914 вступил в Социал-демократическую рабочую партию, в 1916 перешёл в левую Социал-демократическую партию, с 1918 член компартии Нидерландов (КПН). С 1925 член ЦК КПН. В 1929—1930 секретарь окружного комитета КПН в провинции Южная Голландия. С 1930 политический секретарь ЦК КПН. В 1933—37 депутат парламента. На 7-м конгрессе Коминтерна (1935) избран кандидатом в члены ИККИ. В 1937—38 представитель КПН в ИККИ. С 1938 секретарь ЦК КПН. После оккупации Нидерландов немецко-фашистскими войсками (май 1940) вошёл (в октябре 1943) в нелегальное руководство партии. В ноябре 1943 схвачен и затем расстрелян гитлеровцами.
Схаутен Биллем Корнелис
Сха'утен,Схоутен (Schouten) Биллем Корнелис [1580(?), Хорн, провинция Северная Голландия, — 1625], голландский мореплаватель, начальник торговой экспедиции, посланной совместно с Я.
в 1615 западным путём в Индонезию. Его отчёт о кругосветном плавании, изданный в Амстердаме в 1618 под названием «Journal ou description du merveilleux vouage», многократно переиздавался. В честь С. названы открытые им острова близ северо-восточного побережья острова Новая Гвинея.
Схаутен Ян Арнольдус
Сха'утен(Schouten) Ян Арнольдус (р. 1883), нидерландский математик; см.
Я. А.
Схема (в конструкт. документации)
Схе'мав конструкторской документации, документ, на котором условными графическими обозначениями показаны составные части изделия (или установки) и соединения или связи между ними. С. выполняются, как правило, без учёта масштаба и действительного пространственного расположения составных частей изделия. В зависимости от типа элементов изделий и вида связей между ними С. подразделяют на электрические, пневматические, гидравлические, кинематические и комбинированные; в соответствии с назначением различают С. структурные, функциональные, принципиальные, соединений, подключений, общие, расположения.
Структурная С. (блок-схема) определяет основные функциональные части изделия (установки), их назначение и взаимосвязи; она разрабатывается при проектировании (конструировании) изделия, раньше С. др. типов, и используется при изучении структуры изделия и программы его работы, а также во время его эксплуатации. Функциональная С. раскрывает процессы, протекающие в изделии и его отдельных частях; используется при изучении функциональных возможностей изделий, а также при их наладке, регулировке, контроле и ремонте. Принципиальная С. определяет полный состав элементов изделия и связей между ними и, как правило, даёт детальное представление о принципе работы изделия; служит основанием для разработки др. конструкторских документов, например электромонтажных чертежей, спецификации. С. соединений (внутренних и внешних) отображает связи составных частей изделия, способы прокладки, крепления или подсоединения проводов, кабелей или трубопроводов, а также места их присоединения или ввода. На С. подключений показывают внешние подключения изделия; эти С. используют при монтаже и эксплуатации комплексов. Общая С. определяет составные части комплекса (сложного изделия) и соединения их между собой на месте эксплуатации; предназначена преимущественно для общего ознакомления с комплексами. На С. расположения показывается относительное размещение (местоположение) составных частей установки или комплекса. В СССР порядок оформления С. устанавливается ГОСТами.
В. Н. Квасницкий.
Схема (набросок)
Схе'ма(от греч. sch
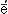
ma — наружный вид, форма, набросок, очерк),
1) изображение, описание, изложение чего-либо в общих, главных чертах.
2) Чертёж, воспроизводящий обычно с помощью условных обозначений и без соблюдения масштаба основную идею какого-либо устройства, сооружения и т. д. См. также
в конструкторской документации.
«Схема тела»
«Схе'ма те'ла»,отражение в сознании человека образа собственного тела (его контуров, размеров, границ, соотносительного положения частей тела, а также одежды, обуви и привычных предметов и средств деятельности — инструментов, протезов и т. п.). «С. т.» — это пластичное представление, которое непрерывно формируется и перестраивается у человека в течение его жизни. Понятие «С. т.» разрабатывается в связи с изучением различных психических нарушений (деперсонализация, нарушение восприятия правого и левого, неузнавание или пространственное отчуждение членов собственного тела вплоть до фантома ампутированных конечностей и образования «двойника») в целях топической диагностики (например, поражения правой теменной области), а также для решения практических задач протезирования. В авиационной и космической психологии понятием «С. т.» пользуются при разработке проблем ориентировки человека в пространстве (схемы «человек — корабль — окружающее пространство», иллюзии пространственного положения).
Лит.:Меерович Р. И., Расстройства «схемы тела» при психических заболеваниях, Л., 1948; Гиляровский В. А., Что такое «схема тела» в свете данных наших физиологов, «Вестник Академии медицинских наук СССР», 1958, № 10; Горбов Ф. Д., Проблемы космической психофизиологии, в сборнике: Человек вышел в космическое пространство, М., 1966.
Ф. Д. Горбов.
Схемотехника
Схемоте'хника,научно-техническое направление, охватывающее проблемы проектирования и исследования
электронных устройств радиотехники и связи, вычислительной техники, автоматики и др. областей техники. Основная задача С. — синтез (определение структуры) электронных схем, обеспечивающих выполнение определённых функций, и расчёт параметров входящих в них элементов. Термин «С.» появился в 60-х гг. 20 в. в связи с разработкой унифицированных схем, пригодных одновременно для многих применений.
На основе электронной схемы создают соответствующее устройство (входящее в состав некоторой технической системы). К устройству предъявляется требование надёжной работы в течение заданного времени в реальных условиях производственного разброса параметров элементов и их старения, влияния внешней среды и возмущающих воздействий. Поэтому при разработке схем наряду с расчётом номинальных значений параметров элементов необходимо рассчитывать эксплуатационные допуски на них, предусматривать в схеме средства, повышающие надёжность устройства (обеспечивающие устойчивую работу схемы при внешних воздействиях), а также позволяющие контролировать его исправность.
Элементной базой для создания электронных устройств служат дискретные электро- и радиоэлементы (резисторы, конденсаторы, диоды, транзисторы и т. д.) и интегральные микросхемы (ИС, см.
)
.Если электронная схема реализуется в виде ИС либо нескольких ИС, то говорят о «микросхемотехнике», под которой понимают область
,связанную с проектированием ИС. Помимо синтеза и расчёта электронных схем, микросхемотехника решает задачу разработки на основе электронных схем структуры (топологии) ИС. Основные этапы разработки: расчёт геометрических размеров элементов ИС; рациональное размещение элементов на поверхности или в объёме подложки ИС; нахождение оптимальных соединений элементов (возможные критерии оптимальности — обеспечение минимальных длин проводников, либо числа их пересечений, либо взаимного влияния и т. д.). Так как создание новой ИС — комплексная проблема, то её решают совместно специалисты по микросхемотехнике, физики, технологи, конструкторы, используя комплексные опытно-теоретические методы, в том числе моделирование на ЭВМ как самой схемы, так и условий её работы.
Теоретической базой С. (в том числе микросхемотехники) служат теория линейных и нелинейных электрических цепей, электродинамика, математическое программирование, теория автоматов и др. При создании электронных схем перспективно использование методов проектирования с применением ЭВМ (см. в ст.
)
.По мере развития микроэлектроники, разработки больших ИС (БИС) — функциональных устройств, представляющих собой целые системы, С. по ряду аспектов сливается с
Лит.:Алексенко А. Г., Основы микросхемотехники, М., 1971; Поспелов Д. А., Логические методы анализа и синтеза схем, 3 изд., М., 1974.
Г. И. Веселов.
Схендел Артур ван
Схе'ндел(Schendel) Артур ван (5.3. 1874, Батавия, ныне Джакарта, Индонезия, — 11.9.1946, Амстердам), нидерландский писатель. Был учителем английского языка. В романах «Влюблённый бродяга» (1904), «Заблудший бродяга» (1907), «Цветы любви» (1921), в новелле «Анджолино и весна» (1923) С. рисовал романтическую среду вне времени и пространства. В романс «Клипер “Иоганна Мария”» (1930, рус. пер. 1966) он обратился к реальности. Углубление социальных мотивов, стремление дать правдивую картину жизни буржуазных Нидерландов выразились в романах «Человек с реки» (1933), «Голландская драма» (1935), «Мир — это праздник танца» (1938). Автор стилизованных под народные повестушки «Воспоминаний одного глупца» (1934) и романа «Менеер Оберон и жена» (1940), антифашистской поэмы «Нидерланды» (1945). Кризисные настроения послевоенных лет сказались в автобиографической книге «Проходящие тени» (опубликована в 1948).
Лит.:'s-Gravesande A. van, А. van Schendel, zijn leven en werk, Amst., 1949; Stuiveling G., A van Schendels drie gestalten, в его кн.: Steekproeven, Amst., 1950: Heerikhuizen Fr. W. van, Het werk van A. van Schendel, Amst., 1961.
И. В. Волевич.
Схенокаулон
Схенока'улон,сабадилла (Schoenocaulon), род многолетних луковичных трав семейства лилейных. Листья линейные, удлинённые. Цветки мелкие, в густом длинном колосовидном соцветии на верхушке безлистного стебля (стрелки). Околоцветник из 6 узких свободных листочков. Плод — трёхгнёздная коробочка с 6—9 семенами. Около 10 видов, на юге Северной Америки, в Центр, и Южной Америке, но преимущественно в Мексике. Наиболее известен С. лекарственный, или сабадилла лекарственная, вшивое семя (S. officinale), в горах Мексики, Гватемалы и Венесуэлы. Семена его ядовиты, содержат алкалоиды: вератридин, цевацин, сабадин, верагенин и верацевин. Настойка и отвар семян обладают инсектицидными свойствами, используются против паразитов животных и человека; препарат вератрин (сумма алкалоидов в виде настойки и мази) применяют при суставных болях и невралгиях.
Лит.:Муравьева Д. А.., Гаммерман А. Ф., Тропические и субтропические лекарственные растения, М., 1974.
Схенокаулон лекарственный: а — цветок; б — коробочка; в — семя.
Схерия
Схе'рия,в древнегреческой мифологии сказочный остров, заселённый феаками; последнее местопребывание
перед возвращением на родину. В античности С. иногда отождествляли с островом Керкирой (Корфу).
Схидам
Схида'м(Schiedam), город и порт в Нидерландах, в провинции Южная Голландия, на берегу р. Ньиве-Маас (рукав Рейна), близ г. Роттердам. 79,8 тыс. жителей (1974). Судостроение, электротехническая, пищевая промышленность.
Схизантус
Схиза'нтус,шизантус (Schizanthus), род однолетних травянистых растений семейства паслёновых. Листья, как правило, перисторассечённые. Цветки в метельчатых соцветиях; венчик двугубый с цельными или рассеченными долями. Около 15 видов, в Южной Америке (Чили). Многие С. декоративны. В цветоводстве широко используют С. перистый (S. pinnatus), его сорта и гибриды, более известные под назв. С. визетонский (S. ґ wisetonensis), с цветками различной окраски.
Схизма
Схи'зма(греч. schнsma, буквально — расщепление), разделение христианской церкви на католическую и православную. См.
.
Схизогнатизм
Схизогнати'зм(биологический), то же, что
.
Схима
Схи'ма(от среднегреч. sch
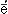
ma — монашеское облачение, буквально — наружный вид, форма), высшая монашеская степень в православной церкви. Посвященные в С. — схимонахи и схимонахини (или схимники) — дают обеты выполнения более суровых монашеских правил, делящихся в зависимости от трудности на великую С. и малую С.
Схистоцерка
Схистоце'рка,насекомое отряда прямокрылых; то же, что
.
Сход сельский
Сход се'льский,собрание крестьян-домохозяев — членов
в дореволюционной России. Ведал приёмом в сельское общество и исключением из него, распределением земли между членами общества, раскладкой оброка, общинных и казённых повинностей, избирал сельскую старосту и др. должностных лиц. Подчинялся полиции,
,
.Собрание крестьян, решавших хозяйственные вопросы в первые годы Советской власти, называлось земельным сходом.
Схода точка
Схо'да то'чка,кажущаяся точка пересечения параллельных линий при изображении в
.На перспективных изображениях С. т. параллельных прямых находится в пересечении плоскости картины с лучом зрения, параллельным этим прямым. См. также
.
Сходимости точка
Сходи'мости то'чкафункционального ряда
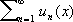 ,
,такая точка
x
0
,что числовой
,составленный из значений функции
u
n
(x)в данной точке
x
0
,является сходящимся. Аналогично определяется С. т. для функциональной последовательности.
Сходимость
Сходи'мость,математическое понятие, означающее, что некоторая переменная величина имеет
.В этом смысле говорят о С. последовательности, С. ряда, С. бесконечного произведения, С. непрерывной дроби, С. интеграла и т. д. Понятие С. возникает, например, когда при изучении того или иного математического объекта строится последовательность более простых в известном смысле объектов, приближающихся к данному, то есть имеющих его своим пределом (так, для вычисления длины окружности используется последовательность длин периметров правильных многоугольников, вписанных в окружность; для вычисления значений функций используются последовательности частичных сумм рядов, которыми представляются данные функции, и т. п.).
С. последовательности {
an}
, n= 1, 2,..., означает существование у неё конечного предела
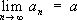
; С. ряда
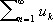 —
—конечного предела (называемого суммой ряда) у последовательности его частичных сумм
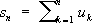
,
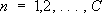
; С. бесконечного произведения
b
1b
2... b
n—конечного предела, не равного нулю, у последовательности конечных произведений
p
n= b
1b
2... b
n, n =1, 2,...;
С. интеграла
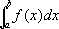
от функции
f(
x)
,интегрируемой по любому конечному отрезку [
а, b]
,—конечного предела у интегралов при
b® +µ, называется
.
Свойство С. тех или иных математических объектов играет существенную роль как в вопросах теории, так и в приложениях математики. Например, часто используется представление каких-либо величин или функций с помощью сходящихся рядов; так, для основания натуральных логарифмов
еимеется разложение его в сходящийся ряд
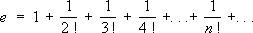
для функции sin
х —в сходящийся при всех
хряд
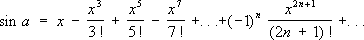
Подобные ряды могут быть использованы для приближённого вычисления рассматриваемых величин и функций. Для этого достаточно взять сумму нескольких первых членов, при этом чем больше их взять, тем с большей точностью будет получено нужное значение. Для одних и тех же величин и функций имеются различные ряды, суммой которых они являются, например,
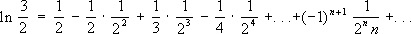
,
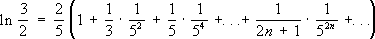
.
При практических вычислениях в целях экономии числа операций (а следовательно, экономии времени и уменьшения накопления ошибок) целесообразно из имеющихся рядов выбрать ряд, который сходится «более быстро». Если даны два сходящихся ряда
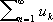
и
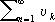 ,
,и
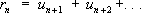
,
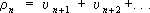 . —
. —их остатки, то 1-й ряд называется сходящимся быстрее 2-го ряда, если
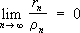
.
Например, ряд
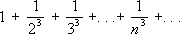
сходится быстрее ряда
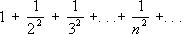
.
Используются и другие понятия «более быстро» сходящихся рядов. Существуют различные методы улучшения С. рядов, то есть методы, позволяющие преобразовать данный ряд в «более быстро» сходящийся. Аналогично случаю рядов вводится понятие «более быстрой» С. и для несобственных интегралов, для которых также имеются способы улучшения их С.
Большую роль понятие С. играет при решении всевозможных уравнений (алгебраических, дифференциальных, интегральных), в частности при нахождении их численных приближённых решений. Например, с помощью
можно получить последовательность функций, сходящихся к соответствующему решению данного обыкновенного дифференциального уравнения, и тем самым одновременно доказать существование при определённых условиях решения и дать метод, позволяющий вычислить это решение с нужной точностью. Как для обыкновенных дифференциальных уравнений, так и уравнений с частными производными существует хорошо разработанная теория различных сходящихся конечноразностных методов их численного решения (см.
)
.Для практического нахождения приближённых решений уравнений широко используются ЭВМ.
Если изображать члены a
n
последовательности {
a
n} на числовой прямой, то С. этой последовательности к
аозначает, что расстояние между точками
a
nи
астановится и остаётся сколь угодно малым с возрастанием
n.В этой формулировке понятие С. обобщается на последовательности точек плоскости, пространства и более общих объектов, для которых может быть определено понятие расстояния, обладающее обычными свойствами расстояния между точками пространства (например, на последовательности векторов, матриц, функций, геометрических фигур и т. д., см.
)
.Если последовательность {
a
n} сходится к
а,то вне любой окрестности точки
алежит лишь конечное число членов последовательности. В этой формулировке понятие С. допускает обобщение на совокупности величин ещё более общей природы, в которых тем или иным образом введено понятие окрестности (см.
)
.
В математическом анализе используются различные виды С. последовательности функций {
f
n(
x)} к функции
f(
x) (на некотором множестве М). Если
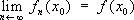
для каждой точки
X
0(из
М)
,то говорят о С. в каждой точке [если это равенство не имеет места лишь для точек, образующих множество меры нуль (см.
)
,то говорят о С. почти всюду]. Несмотря на свою естественность, понятие С. в каждой точке обладает многими нежелательными особенностями [например, последовательность непрерывных функций может сходиться в каждой точке к разрывной функции; из С. функций
f
n(
x) к
f(
x)
в каждой точке не следует, вообще говоря, С. интегралов от функций
f
n(
x) к интегралу от
f(
x) и т. д.]. В связи с этим было введено понятие равномерной С., свободное от этих недостатков: последовательность {
f
n(
x)} называется равномерно сходящейся к
f(
x) на множестве
М,если
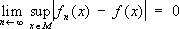
Этот вид С. соответствует определению расстояния между функциями
f(
x) и (
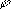
(
х) по формуле
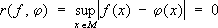
Д. Ф.
доказал, что если последовательность измеримых функций сходится почти всюду на множестве
М,то из
Мможно так удалить часть сколь угодно малой меры, чтобы на оставшейся части имела место равномерная С.
В теории интегральных уравнений, ортогональных рядов и т. д. широко применяется понятие средней квадратической С.: последовательность {
f
n(
x)} сходится на отрезке [
a, b] в среднем квадратическом к
f(
x)
,если
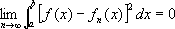
.
Более общо, последовательность {
f
n(
x)} сходится в среднем с показателем
р к f(
x)
,если
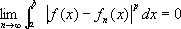
.
Эта С. соответствует заданию расстояния между функциями по формуле
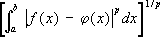
.
Из равномерной С. на конечном отрезке вытекает С. в среднем с любым показателем
р.Последовательность частичных сумм разложения функции
j(х)с интегрируемым квадратом по нормированной
может расходиться в каждой точке, но такая последовательность всегда сходится к
j(х)в среднем квадратическом. Рассматриваются также другие виды С. Например, С. по мере: для любого e > 0 мера множества тех точек, для которых
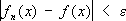 ,
,стремится к нулю с возрастанием
n',слабая С.:
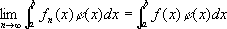
для любой функции
j(x)с интегрируемым квадратом (например, последовательность функций
sinx, sin2x,..., sinnx,... слабо сходится к нулю на отрезке [—p, p], так как для любой функции
j(х) синтегрируемым квадратом коэффициенты
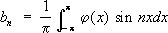
ряда Фурье стремятся к нулю).
Указанные выше и многие другие понятия С. последовательности функций систематически изучаются в функциональном анализе, где рассматриваются различные линейные пространства с заданной нормой (расстоянием до нуля) — так называемые банаховы пространства. В таких пространствах можно ввести понятия С. функционалов, операторов и т. д., определяя для них соответствующим образом норму. Наряду со С. по норме (так называемой сильной С.), в банаховых пространствах рассматривается слабая С., определяемая условием
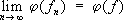
для всех линейных функционалов; введённая выше слабая С. функций соответствует рассмотрению нормы
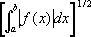
. В современной математике рассматривается также С. по частично упорядоченным множествам (см.
)
.В теории вероятностей для последовательности случайных величин употребляются понятия С. с вероятностью 1 и С. по вероятности.
Ещё математики древности (Евклид, Архимед) по существу употребляли бесконечные ряды для нахождения площадей и объёмов. Доказательством С. рядов им служили вполне строгие рассуждения по схеме
.Термин «С.» в применении к рядам был введён в 1668 Дж.
при исследовании некоторых способов вычисления площади круга и гиперболического сектора. Математики 17 в. обычно имели ясное представление о С. употребляемых ими рядов, хотя и не проводили строгих с современной точки зрения доказательств С. В 18 в. широко распространилось употребление в анализе заведомо расходящихся рядов (в частности, их широко применял Л.
)
.Это, с одной стороны, привело впоследствии ко многим недоразумениям и ошибкам, устранённым лишь с развитием отчётливой теории С., а с другой — предвосхитило современную теорию
расходящихся рядов. Строгие методы исследования С. рядов были разработаны в 19 в. (О.
,Н.
,К
.
,Б
.Больцано и др.). Понятие равномерной С. было введено Дж.
.Дальнейшие расширения понятия С. были связаны с развитием теории функций, функционального анализа и топологии.
Лит.:Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., т. 1—2, М., 1971—73; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1—2, М., 1970; Никольский С. М., Курс математического анализа, т. 1—2, М., 1973.
Сходница
Схо'дница,посёлок городского типа в Львовской области УССР. Подчинён Бориславскому горсовету. Расположен в 9
кмот ж.-д. станции Борислав. Нефтепромысел, лесозавод и др. предприятия. Пансионаты: «Карпаты», «Гуцулка».
Сходня
Схо'дня,город (с 1961) в Химкинском районе Московской области РСФСР, на р. Сходня (приток р. Москвы). Ж.-д. станция в 30
кмк С.-З. от Москвы. 19 тыс. жителей (1974). Стекольный завод, мебельно-сборочный комбинат, галантерейная и трикотажная фабрики. Пушно-меховой техникум. Турбаза.
Сходство
Схо'дство(философский), соответствие отображения, образа своему оригиналу. Понятие С. используется при
.Оно включает три основные отношения: соответствие качественных характеристик отображения особенностям оригинала (например, ощущение зелёного цвета листьев растения соответствует определённой длине электромагнитных волн, излучаемых поверхностью листьев); соответствие структур отображения структурам оригинала (например, структура географической карты соответствует геометрическим структурам местности), причём разные виды соответствия структур могут описываться с помощью различных математических отображений —
,
и др.; соответствие количественных характеристик отображения и оригинала (например, количественные значения состояний термостата соответствует измеряемой температуре тела).
Степень С. (адекватности) отображения оригиналу может оцениваться по следующим характеристикам: достоверность сведений, знаний, а для теоретических построений — доказательность; точность и полнота отображения; глубина, существенность отображения тех или иных свойств, связей и отношений. Диалектико-материалистическое понимание С. противостоит односторонним представлениям о С. как о «зеркальном» отражении в виде «физического подобия» или как об иероглифическом отображении объекта. (См.
.)
Лит.см. при ст.
.
В. С. Тюхтин.
Сходящийся ряд
Сходя'щийся ряд,см.
.
Схождение колёс
Схожде'ние колёс,установка передних колёс автомобиля симметрично под углом к его продольной оси, при этом расстояние между колёсами спереди меньше, чем сзади. С. к. необходимо из-за установки передних колёс с наклоном в вертикальной плоскости (см.
)
,что вызывает их стремление катиться по расходящимся дугам. С. к. позволяет устранить это явление и обеспечивает качение колёс по параллельным прямым. Нарушение С. к. приводит к ускоренному износу шин и ухудшению устойчивости движения автомобиля. С. к. равно разности расстояний (А—Б,
см.
рис.
) и для различных моделей автомобилей находится в пределах 2—8
мм.С. к. можно отрегулировать, удлиняя или укорачивая поперечную или боковые рулевые тяги
1, на которых для этого имеются наконечники с резьбой.
Схождение колёс.
Схоластика
Схола'стика(лат. scholastica, от греч. scholastikуs — школьный, учёный, schol
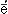
— учёная беседа, школа), тип религиозной философии, характеризующийся принципиальным подчинением примату теологии, соединением догматических предпосылок с рационалистической методикой и особым интересом к формально-логической проблематике; получил наиболее полное развитие и господство в Западной Европе в средние века.
Истоки С. восходят уже к позднеантичной философии, прежде всего к
(установка на вычитывание ответов на все вопросы из текстов Платона, энциклопедическое суммирование разнообразной проблематики, соединение мистических предпосылок с рассудочными выводами). Христианская
подходит к С. по мере завершения работы над догматическими основами церковной доктрины (
)
.Ранняя С. (11—12 вв.) сложилась в условиях подъёма феодальной цивилизации и папской власти; она находилась под влиянием августиновского платонизма (
Кентерберийский). Впервые выявляются противоположные позиции в споре об
—
(Гильом из Шампо) и
(Росцелин), а также промежуточная позиция —
(П.
)
.В этот период С. нередко сталкивается с инерцией фидеистического антиинтеллектуализма; не только доктрины отдельных «еретиков», но принцип схоластического рационализма как таковой вызывает нападки со стороны поборников традиционной линии (Петра Дамиани, Ланфранка,
и др.). Зрелая С. (12—13 вв.) развивалась в средневековых университетах; её общеевропейским центром был Парижский университет. Платонизм (переживший смелое натуралистическое истолкование в философии
,во многом предвосхитившей тенденции Возрождения) постепенно вытесняется аристотелизмом, в интерпретации которого происходит размежевание между «еретическим»
,отрицавшим реальность личной души и учившим о единой безличной интеллектуальной душе во всех существах (
)
,и ортодоксальным направлением С., подчинявшим онтологию Аристотеля христианским представлениям о личном боге, личной душе и сотворённом космосе (
и особенно
)
.Поздняя С. (13—14 вв.) испытала воздействие обострившихся идейных противоречий эпохи развитого феодализма.
противопоставил интеллектуализму системы Фомы Аквинского свой волюнтаризм, отказ от завершенной системы и острый интерес к индивидуальному бытию. Оппозиционные представители этого периода (У.
,отчасти Никола Орем) всё энергичнее настаивают на теории
,разрушавшей схоластическую «гармонию» веры и разума. Возрождение оттеснило С. на периферию умственной жизни. Частичное оживление традиций С. произошло в так называемый второй С. (16—17 вв.), развивавшейся в период Контрреформации, главным образом в Испании (Ф. де Витория, Ф.
,Г. Васкес, М. Молина). Просвещение нанесло второй С. решающий удар. В конце 19—20 вв. традиции С. возрождаются в
(см. также
)
.
С. возникла в условиях, когда церковь выступала в виде «... наиболее общего синтеза и наиболее общей санкции существующего феодального строя» (Энгельс Ф., см. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 7, с. 361) и религия представала одновременно и как универсальная форма не собственно религиозного содержания. Подчинение мысли авторитету догмата (формула Петра Дамиани «философия есть служанка богословия») присуще ортодоксальной С. наравне со всеми др. типами правоверно-церковного мировоззрения; специфично для С. то, что сам характер отношений между разумом и догматом мыслился при несомненной авторитарности довольно рассудочным. Как «священное писание» и «священное предание», так и наследие античной философии, активно использовавшееся С., выступали в ней в качестве замкнутого нормативного текста. Предполагалось, что всякое знание имеет два уровня — «сверхъестественное» знание, даваемое в «откровении», и «естественное», отыскиваемое человеческим разумом; норму первого содержат тексты Библии, сопровождаемые авторитетными комментариями отцов церкви, норму второго — тексты Платона и особенно Аристотеля, окруженные авторитетными комментариями позднеантичных и арабских философов. Потенциально в тех и др. текстах уже дана «вечная истина»; чтобы актуализировать её, надо вывести из текстов полноту их логических следствий при помощи цепи правильно построенных умозаключений (средний характерный для зрелой С. жанр «суммы» — итогового энциклопедического сочинения, содержащего нескончаемое множество ответов на вопросы, выводимых из ограниченного числа «правильных» основоположений). Мышление С. постоянно идёт путём
и почти не знает
;его основная форма —
.В известном смысле вся С. есть философствование в формах интерпретации текста. В этом она противоположна новоевропейской науке с её стремлением открыть истину через анализ опыта, а также
с её стремлением «узреть» истину в экстатическом созерцании. Обиход С., в котором «таинства веры» превращались в ходовые образцы логических задач, вызывал уже в средние века протесты не только представителей вольнодумства, но и ревнителей веры («нелепо спорить о троице на перекрёстках и превращать предвечное рождение бога-сына... в поприще публичного состязания» — восклицал в конце 12 в. Петр из Блуа). Осознание того, что авторитеты противоречат друг другу [афоризмы типа «У авторитета — восковой нос» (который можно повернуть, куда угодно), «аргумент от авторитета — слабейший» были распространены среди самых ортодоксальных схоластов], явилось одним из важных импульсов для становления С. Сопоставление взаимоисключающих текстов было введено гонимым Абеляром (в соч. «Да и нет»), но вскоре стало общепринятой формой: противоречия теологического и философского предания подлежат систематизации и должна быть установлена иерархия авторитетов. Специфика схоластического рационализма не может быть понята вне его связи с традицией юридического мышления (римское право было в Западной Европе одной из наиболее жизнестойких частей античного наследия). В С. имеет место юридическая окраска онтологических категорий и онтологизация юридических категорий; бытие мира и человека, соотносимое с бытием бога, описывается как совокупность правовых отношений или их аналогов; сами приёмы выведения частного из общего, заключений по аналогии и т. п. напоминают разработку юридических «казусов».
Ориентация на жестко фиксированные «правила» мышления помогла С. сохранить преемственность интеллектуальных навыков, необходимый понятийно-терминологический аппарат через реставрацию античного наследия в предельно формализованном виде (даже резко критиковавшие С. мыслители нового времени вплоть до эпохи Просвещения и немецкого классического идеализма принуждены были широко пользоваться схоластической лексикой). Гуманисты Возрождения и особенно философы Просвещения в борьбе со средневековыми традициями выступили против С., подчёркивая всё мёртвое в ней и превратив само слово «С.» в бранную кличку бесплодного и бессодержательного умствования, пустой словесной игры. Утверждая догматическую сумму представлений, С. не способствовала развитию естественных наук, однако её структура оказалась благоприятной для таких, например, областей знания, как логика; достижения схоластов в этой сфере предвосхищают современную постановку многих вопросов, в частности математической логики (см.
,раздел История логики).
Лит.:Владиславлев М. И., Схоластическая логика, «Журнал Министерства народного просвещения», 1872, ч. 162, [№ 8], отд. 2; Эйкен Г., История и система средневекового миросозерцания, пер. с нем., СПБ, 1907; Штекль А., История средневековой философии, пер. с нем., М., 1912; Трахтенберг О. В., Очерки по истории западноевропейской средневековой философии, М., 1957; Стяжкин Н. И., Формирование математической логики, М., 1967; Gilson Е., L'йsprit de la philosophic mйdiйvale, 2 йd., P., 1944; Copleston F., A history of philosophy, v. 2—3, L., 1951—53; Grabmann М., Die Geschichte der scholastischen Methode, Bd 1—2, В., 1957.
С. С. Аверинцев.
Схолиасты
Схолиа'сты(греч. scholiastбi), составители
.
Схолия
Схо'лия(греч. schуlia, множественное число от schуlion — толкование, объяснение), пояснительные заметки на полях античных (главным образом греческих) и средневековых рукописей. Впервые слово «С.» встречается у Галена (2 в. н. э.). В отличие от комментариев, С. разъясняли не текст целиком, а отдельные пассажи у античных классиков, в Библии, у раннехристианских авторов. Первым схолиастом считают грамматика Дидима Александрийского (1 в. н. э.). Различают древние С., восходящие к античным филологам (Аристарх, Зенодот и др.), и новые (позднеантичные и средневековые). Значительная часть средневековой С. анонимна. Деятельность схолиастов прекращается в 15—16 вв.
Схоутен Ян Арнольдус
Схо'утен,Схаутен (Schouten) Ян Арнольдус (р. 28.8.1883, Амстердам), нидерландский математик, член Нидерландской королевской академии наук (1933). В 1908 окончил Высшую техническую школу в Делфте, в 1914—43 профессор там же. Основные исследования относятся к тензорной дифференциальной геометрии и её приложениям. Автор работ, посвященных проблеме Пфаффа и релятивистской физике.
Соч. в рус. пер.: Тензорный анализ для физиков, М., 1965.
Схрейнемакерс Францискус Антониус Хубертус
Схре'йнемакерс(Schreinemakers) Францискус Антониус Хубертус (1.9.1864, Рурмонд, — 1945), нидерландский физикохимик. С 1901 профессор Лейденского университета. Основные труды С. относятся к области гетерогенных равновесий в тройных и многокомпонентных системах. Им предложен так называемый метод остатков (1893), позволяющий определять химический состав твёрдых фаз, кристаллизующихся в тройных системах без отделения этих фаз от маточного раствора. Даны способы изображения равновесий в тройных (1892) и в четверных системах (1907—09), рассмотрены равновесия в тройных системах с областями расслоения (1913), а также установлены диаграммы состояния многих водно-соляных тройных и четверных систем. Работы С. широко используются в физико-химическом анализе, петрографии, металлургии и галургии.
Лит.:Jorissen W. P., F. А. Н. Schreinemakers, «Chemisch weekbiad», 1923, Jahr-gang 20, № 27 (имеется список трудов С.).
Схул
Схул,Эс-Схул, пещера в Палестине, где найдены костные остатки ископаемых людей. См. в ст.
.

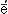 ma — наружный вид, форма, набросок, очерк),
ma — наружный вид, форма, набросок, очерк),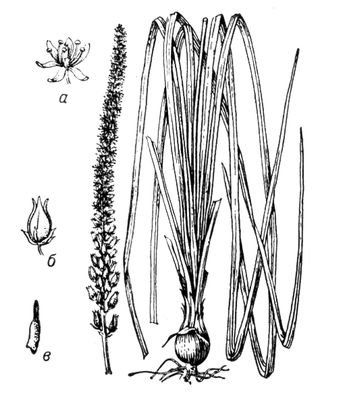
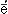 ma — монашеское облачение, буквально — наружный вид, форма), высшая монашеская степень в православной церкви. Посвященные в С. — схимонахи и схимонахини (или схимники) — дают обеты выполнения более суровых монашеских правил, делящихся в зависимости от трудности на великую С. и малую С.
ma — монашеское облачение, буквально — наружный вид, форма), высшая монашеская степень в православной церкви. Посвященные в С. — схимонахи и схимонахини (или схимники) — дают обеты выполнения более суровых монашеских правил, делящихся в зависимости от трудности на великую С. и малую С.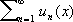 ,такая точка
x
0
,что числовой
,такая точка
x
0
,что числовой
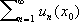
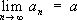 ; С. ряда
; С. ряда
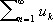 —конечного предела (называемого суммой ряда) у последовательности его частичных сумм
—конечного предела (называемого суммой ряда) у последовательности его частичных сумм
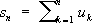 ,
,
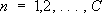 ; С. бесконечного произведения
b
1b
2... b
n—конечного предела, не равного нулю, у последовательности конечных произведений
p
n= b
1b
2... b
n, n =1, 2,...;
С. интеграла
; С. бесконечного произведения
b
1b
2... b
n—конечного предела, не равного нулю, у последовательности конечных произведений
p
n= b
1b
2... b
n, n =1, 2,...;
С. интеграла
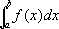 от функции
f(
x)
,интегрируемой по любому конечному отрезку [
а, b]
,—конечного предела у интегралов при
b® +µ, называется
от функции
f(
x)
,интегрируемой по любому конечному отрезку [
а, b]
,—конечного предела у интегралов при
b® +µ, называется
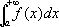
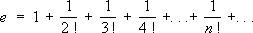
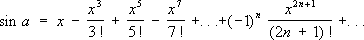
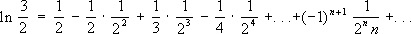 ,
,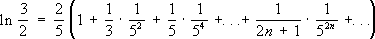 .
.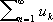 и
и
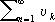 ,и
,и
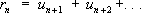 ,
,
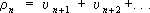 . —их остатки, то 1-й ряд называется сходящимся быстрее 2-го ряда, если
. —их остатки, то 1-й ряд называется сходящимся быстрее 2-го ряда, если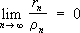 .
.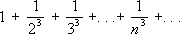
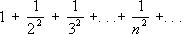 .
.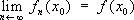 для каждой точки
X
0(из
М)
,то говорят о С. в каждой точке [если это равенство не имеет места лишь для точек, образующих множество меры нуль (см.
)
,то говорят о С. почти всюду]. Несмотря на свою естественность, понятие С. в каждой точке обладает многими нежелательными особенностями [например, последовательность непрерывных функций может сходиться в каждой точке к разрывной функции; из С. функций
f
n(
x) к
f(
x)
в каждой точке не следует, вообще говоря, С. интегралов от функций
f
n(
x) к интегралу от
f(
x) и т. д.]. В связи с этим было введено понятие равномерной С., свободное от этих недостатков: последовательность {
f
n(
x)} называется равномерно сходящейся к
f(
x) на множестве
М,если
для каждой точки
X
0(из
М)
,то говорят о С. в каждой точке [если это равенство не имеет места лишь для точек, образующих множество меры нуль (см.
)
,то говорят о С. почти всюду]. Несмотря на свою естественность, понятие С. в каждой точке обладает многими нежелательными особенностями [например, последовательность непрерывных функций может сходиться в каждой точке к разрывной функции; из С. функций
f
n(
x) к
f(
x)
в каждой точке не следует, вообще говоря, С. интегралов от функций
f
n(
x) к интегралу от
f(
x) и т. д.]. В связи с этим было введено понятие равномерной С., свободное от этих недостатков: последовательность {
f
n(
x)} называется равномерно сходящейся к
f(
x) на множестве
М,если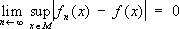
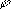 (
х) по формуле
(
х) по формуле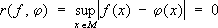
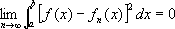 .
.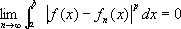 .
.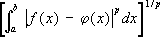 .
.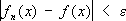 ,стремится к нулю с возрастанием
n',слабая С.:
,стремится к нулю с возрастанием
n',слабая С.: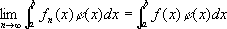
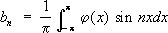 ряда Фурье стремятся к нулю).
ряда Фурье стремятся к нулю).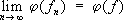 для всех линейных функционалов; введённая выше слабая С. функций соответствует рассмотрению нормы
для всех линейных функционалов; введённая выше слабая С. функций соответствует рассмотрению нормы
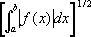 . В современной математике рассматривается также С. по частично упорядоченным множествам (см.
)
.В теории вероятностей для последовательности случайных величин употребляются понятия С. с вероятностью 1 и С. по вероятности.
. В современной математике рассматривается также С. по частично упорядоченным множествам (см.
)
.В теории вероятностей для последовательности случайных величин употребляются понятия С. с вероятностью 1 и С. по вероятности.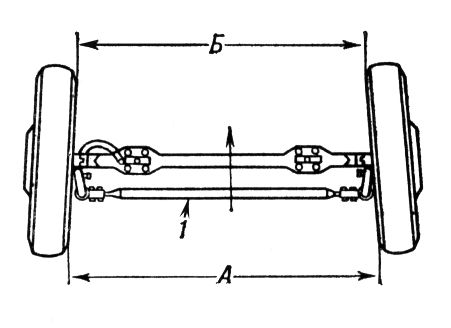
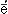 — учёная беседа, школа), тип религиозной философии, характеризующийся принципиальным подчинением примату теологии, соединением догматических предпосылок с рационалистической методикой и особым интересом к формально-логической проблематике; получил наиболее полное развитие и господство в Западной Европе в средние века.
— учёная беседа, школа), тип религиозной философии, характеризующийся принципиальным подчинением примату теологии, соединением догматических предпосылок с рационалистической методикой и особым интересом к формально-логической проблематике; получил наиболее полное развитие и господство в Западной Европе в средние века.