 |
|
|
|
()ModernLib.Net / / / () - (. 2)
С. э. постоянного тока применяют для учёта расхода электроэнергии на подвижном составе электрифицированного ж.-д. транспорта, на электролизных установках (в условных единицах — вольт-часах) ,для измерения количества электричества (в ) ,прошедшего через аккумуляторную батарею при её зарядке; С. э. переменного тока применяют как квартирные счётчики электроэнергии и для учёта расхода электроэнергии в электроприводах, осветительных сетях, коммунальном хозяйстве и т. п. Погрешность измерения С. э. 1—2,5%. Лит.:Электрические измерения. Средства и методы измерений, под ред. Е. Г. Шрамкова, М., 1972; Шкурин Г. П., Справочник по электро- и электронноизмерительным приборам, М., 1972; Касаткин А. С., Электротехника, 3 изд., М., 1973. Г. П. Шкурин.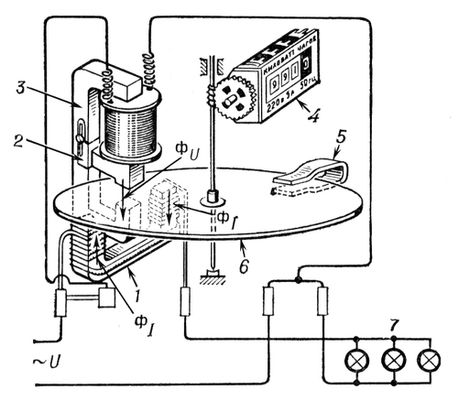 
Индукционный однофазный счётчик электроэнергии переменного тока (50 гц): Ф U— поток, создаваемый током в цепи напряжения (параллельной нагрузке); Ф I— поток, создаваемый током нагрузки; 1 — электромагнит последовательной цепи (тока); 2 — металлическая пластинка для регулирования угла сдвига фаз между потоками Ф Uи Ф I; 3 — электромагнит параллельной цепи (напряжения); 4 — счётный механизм; 5 — тормозной магнит (постоянный магнит, который создаёт противодействующий момент, необходимый для обеспечения однозначности измерения); 6 — алюминиевый диск; 7 — нагрузка (например, осветительные лампы накаливания). Счётчик ядер конденсации Счётчик я'дер конденса'ции,прибор для определения концентрации (числа в единице объёма воздуха, обычно в 1 см 3) в атмосфере. Наибольшее распространение получили С. я. к., основанные на принципе адиабатических камер. Исследуемый объём воздуха вводится в небольшую увлажнённую камеру, которая затем адиабатически расширяется, воздух при этом охлаждается, водяной пар становится пересыщенным и конденсируется на ядрах конденсации. Образовавшиеся капельки оседают на дно камеры, и их считают с помощью лупы. На этом принципе работают счётчики Д. Айткена (1887) и Шольца (1932). Последний позволяет определять концентрацию ядер почти во всём диапазоне концентраций, встречающихся в атмосфере; одна из моделей даёт возможность измерять раздельно число заряженных и нейтральных ядер. Существуют фотоэлектрические С. я. к., основанные на измерении интенсивности света, проходящего через камеру, в которой после её расширения на ядрах конденсации образовались капли (туман). Чем больше концентрация капель, а следовательно, и ядер конденсации, тем больше ослабление светового луча, направленного через камеру-трубку на фотоэлемент; фототок регистрируется гальванометром. Для перехода к концентрации ядер конденсации прибор предварительно градуируется. Преимущество этих С. я. к. — объективность показаний и возможность автоматизации их работы. Лит.:Грабовский Р. И., Атмосферные ядра конденсации, Л., 1956; Александров Н. Н., Петренчук О. П., Методика измерения ядер конденсации в свободной атмосфере при самолётных зондированиях, «Труды Главной геофизической обсерватории», 1959, в. 93; Лактионов А. Г., Определение концентрации облачных ядер конденсации, «Докл. АН СССР. Серия математика, физика», 1965, т. 165, № 6. Е. С. Селезнева. Счётчики заряженных частиц Счётчики заря'женных части'ц,приборы для регистрации заряженных частиц. К ним относятся: , , , и некоторые др. . Счёты Счёты,прибор для арифметических вычислений ( ). Несмотря на применение совершенных счётных машин, С. не утратили своего значения при практической счётной работе. Прообразом современных С. явился так называемый дощаный счёт, возникший впервые в России в 16 в. Большое влияние на создание дощаного счёта оказала система налогового обложения в России 15—17 вв. (сошное письмо), при которой, наряду со сложением, вычитанием, умножением и делением целых чисел, надо было производить те же операции и с дробями, поскольку условная единица обложения — соха, делилась на части. Дощаный счёт представлял собой два складывающихся ящика. Каждый ящик разгораживался надвое (позже только внизу); второй ящик был необходим ввиду особенностей денежного счёта. Внутри ящика на натянутые шнуры или проволоку нанизывались кости. В соответствии с десятичной системой счисления ряды для целых чисел имели по 9 или 10 костей (
рис. 2
); операции с дробями производились на неполных рядах: ряд из трёх костей составлял три трети, ряд из четырёх костей — четыре четверти (чети). Ниже располагались ряды, в которых было по одной кости: каждая кость представляла половину от той дроби, под которой она располагалась (например кость расположенная под рядом из трех костей, составляла половину от одной трети, кость под ней — половину от половины одной трети, и т. д.). Дроби суммировались без приведения к общему знаменателю, например «четь да полтрети, да полполчети»
С переходом к арабским цифрам и отменой сошного письма С. утратили в конце 17 в. ряды для дробей, а в начале 18 в. лишились второго ящика и приобрели свой современный вид (сохранившийся в С. один неполный ряд, обычно из четырёх костей, отделяет два ряда для десятых и сотых единицы, а также иногда служит для счёта четвертей и половинок). За границей русские С. применяются в Иране, а в Западной Европе — созданные на их основе в 19 в. наглядные пособия для школы. Китайские С. (суан-пан, рис. 3 ), принятые также в Индокитае и Японии, значительно старше русских и поныне сохраняют своё древнее устройство со счётом единиц до 5, а далее пятками. Лит.:Спасский И. Г., Происхождение и история русских счетов, в кн.: Историко-математические исследования, в. 5, М., 1952.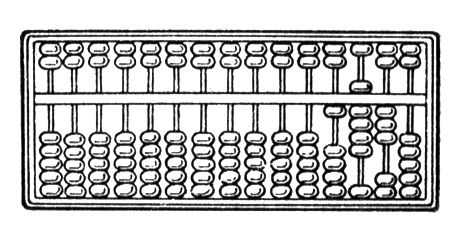 
Рис. 3. Суан-пан (китайские счёты). Положено 1930. 
Рис. 2. Дощаный счет (по чертежу 17 в.). Положено слева
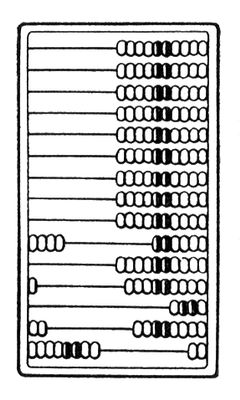
Рис. 1. Счёты. Положено 401,28. Счисление Счисле'ние,нумерация, совокупность приёмов наименования и обозначения чисел. Наиболее совершенным принципом представления чисел является позиционный (поместный) принцип, согласно которому один и тот же числовой знак ( ) имеет различные значения в зависимости от того места, где он расположен. Такая система С. основывается на том, что некоторое число nединиц (основание системы С.) объединяется в одну единицу второго разряда, nединиц второго разряда объединяются в одну единицу третьего разряда и т. д. Основанием системы С. может быть любое число, большее единицы. К числу таких систем относится современная десятичная система С. (с основанием n =10). В ней для обозначения первых десяти чисел служат цифры 0, 1,..., 9 (см. ) . Несмотря на кажущуюся естественность такой системы С., она явилась результатом длительного исторического развития. Возникновение десятичной системы С. связано со счётом на пальцах. Имелись системы С. и с другим основанием: 5, 12 (счёт дюжинами), 20 (следы такой системы сохранились во французском языке, например quatre-vingts, то есть буквально четыре-двадцать, означает 80), 40, 60 и др. При научных исследованиях и при вычислениях на современных вычислительных машинах часто применяется система С. с основанием 2 (см. ) .
У первобытных народов не существовало развитой системы С. Ещё в 19 в. у многих племён Австралии и Полинезии было только два числительных: один и два; сочетания их образовывали числа: 3 — два-один, 4 — два-два, 5 — два-два-один и 6 — два-два-два. О всех числах, больших 6, говорили: «много», не индивидуализируя их. С развитием общественно-хозяйственной жизни возникла потребность в создании систем С., которые позволили бы считать и обозначать всё большие совокупности предметов. Одной из наиболее древних систем С. является египетская иероглифическая нумерация, возникшая ещё за 2500—3000 лет до н. э. Это была десятичная непозиционная система С., в которой для записи чисел применялся только принцип сложения (числа, выраженные рядом стоящими цифрами, складываются). Специальные знаки имелись для единицы
Для 10 000 был введён новый знак М. Тем не менее ионийская система С. оказалась непригодной уже для астрономических вычислений эпохи эллинизма, и греческие астрономы этого времени стали комбинировать алфавитную систему с шестидесятеричной вавилонской — первой известной нам системой С., основанной на позиционном принципе. В системе С. древних вавилонян, возникшей примерно за 2000 лет до н. э., все числа записывались с помощью двух знаков:
Современная десятичная позиционная система С. возникла на основе нумерации, зародившейся не позднее 5 в. в Индии. До этого в Индии имелись системы С., в которых применялся не только принцип сложения, но и принцип умножения (единица какого-нибудь разряда умножается на стоящее слева число). Аналогично строились старокитайская система С. и некоторые др. Если, например, условно обозначить число 3 символом III, а число 10 символом X, то число 30 запишется как IIIX (три десятка). Такие системы С. могли служить подходом к созданию десятичной позиционной нумерации. Десятичная позиционная система С. даёт принципиальную возможность записывать сколь угодно большие числа. Запись чисел в ней компактна и удобна для производства арифметических операций. Поэтому вскоре после возникновения десятичная позиционная система С. начинает распространяться из Индии на Запад и Восток. В 9 в. появляются рукописи на арабском языке, в которых излагается эта система С., в 10 в. десятичная позиционная нумерация доходит до Испании, в начале 12 в. она появляется и в других странах Европы. Новая система С. получила название арабской, потому что в Европе с ней познакомились впервые по латинским переводам с арабского. Только в 16 в. новая нумерация получила широкое распространение в науке и в житейском обиходе. В России она начинает распространяться в 17 в. ив самом начале 18 в. вытесняет алфавитную. С введением десятичная позиционная система С. стала универсальным средством для записи всех действительных чисел. Лит.:Кэджори ф.. История элементарной математики с указаниями на методы преподавания, пер. с англ., 2 изд., Од., 1917; Леффлер Е., Цифры и цифровые системы культурных народов в древности и в новое время, пер. с нем., Од., 1913; Выгодский М. Я., Арифметика и алгебра в древнем мире, 2 изд., М., 1967; Башмакова И. Г. и Юшкевич А. ГГ., Происхождение систем счисления, в кн.: Энциклопедия элементарной математики, кн. 1, М.—Л., 1951. И. Г. Башмакова. Счисление пути Счисле'ние пути'судна, непрерывный учёт элементов движения судна (скорости, направления) и воздействий внешних сил с целью определения координат судна (счислимого места) без наблюдения береговых ориентиров и небесных светил ( ) .С. п. определяют положение судна с точностью, необходимой для плавания и обеспечения навигационной безопасности. С. п. производится на основании значений курса, скорости и вектора сноса судна. Графическое С. п. ведётся на карте, в его процессе осуществляются расчёт и прокладка истинных курсов и пройденных расстояний, учёт и сноса судна. При таком С. п. с помощью счислимое место получают непрерывно, при ручном способе — дискретно, с избранным интервалом времени. Аналитическое С. п. выполняется с помощью счётно-решающих устройств. Считывание информации Счи'тывание информа'циив ЦВМ, извлечение информации, хранящейся в (ЗУ), и передача её в др. устройства вычислительной машины. С. и. производится при выполнении большинства машинных ,а иногда является самостоятельной операцией. Считывание может сопровождаться разрушением (стиранием) информации в тех ячейках (зонах) ЗУ, откуда производилось считывание (как, например, в ЗУ на ферритовых сердечниках), или быть неразрушающим (например, в ЗУ на магнитных лентах, дисках) и, следовательно, допускающим многократное использование однажды записанной информации. С. и. характеризуется временем, затрачиваемым непосредственно на вывод данных из ЗУ; оно составляет от нескольких десятков нсекдо нескольких мсек.(См. также .) 1, 2 |
|||||||
. Иногда операции с дробями производились как с целыми при помощи приравнивания целого (сохи) к определённой сумме денег. Например, при равенстве соха = 48 денежным единицам приведённая выше дробь составит 12 + 8 + 3 = 23 денежные единицы.
, справа 30 рублей 18 алтын
деньги.
, десяти
, ста
и других десятичных разрядов 10
7
.Число 343 записывалось так
(здесь.
— 300,
— 40,
—3), в славянской:
. В алфавитных системах С. запись чисел гораздо короче, чем в предыдущих; кроме того, над числами, записанными в алфавитной нумерации, гораздо легче производить арифметические действия. Однако в алфавитных системах С. нельзя записывать сколь угодно большие числа. Греки расширили ионийскую нумерацию: числа 1000, 2000,..., 9000 они обозначали теми же буквами, что и 1, 2,..., 9, но ставили штрих внизу слева: так, `a означала 1000, `b — 2000 и т. д.
(для единицы) и
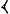(для десяти). Числа до 60 записывались как комбинация этих двух знаков с применением принципа сложения. Число 60 снова обозначалось знаком
,являясь единицей высшего разряда. Для записи чисел от 60 до 3600 вновь применялся принцип сложения, а число 36 000 обозначалось тем же знаком, что и единица, и т. д. Число 343 = 5 60 + 4
.10+3 в этой системе записывалось так: . Однако в силу отсутствия знака для нуля, которым можно было бы отмечать недостающие разряды, запись чисел в этой системе С. не была однозначной (см.
)
.Другая система С., основанная на позиционном принципе, возникла у индейцев майя, обитателей полуострова Юкатан (Центральная Америка) в середине 1-го тысячелетия н. э. У майя существовали две системы С.: одна, напоминающая египетскую, употреблялась в повседневной жизни, Другая — позиционная, с основанием 20 и особым знаком для нуля, применялась при календарных расчётах. Запись в этой системе, как и в нашей современной, носила абсолютный характер.