|
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (РИ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (РИ) - Чтение (стр. 12)
В достаточно малой окрестности такое соответствие будет взаимно однозначным; если ввести в касательном пространстве декартовы координаты
x
1,..., x
nи приписать их значения соответствующим точкам окрестности
U,то между линейными элементами
dsриманова и
ds
oевклидова пространств будет такая связь:
i= 1, …, n. откуда следует, что разность ds - ds oимеет порядок не ниже, чем
Евклидово пространство, поставленное в такое соответствие с римановым, и называется соприкасающимся (в отличие от обычного касательного пространства). Добиться более высокого порядка совпадения за счёт специального выбора соответствия между римановым и евклидовым пространствами в общем случае уже невозможно. Поэтому коэффициенты R mlkiхарактеризуют отличие риманова пространства от евклидова; они являются компонентами так называемого тензора кривизны (или тензора Римана - Кристоффеля), определяемого по формуле
лишь через g ik,и их производные до второго порядка. Тождественное обращение в нуль тензора кривизны необходимо и достаточно для того, чтобы пространство в окрестности каждой точки совпадало с евклидовым (в целом оно может отличаться от него своим строением, подобно тому как боковая поверхность цилиндра отличается от плоскости). Параллельное перенесение.Для всякой гладкой кривой Lриманова пространства существует отображение её окрестности U Lв евклидово пространство E Lпри котором оно оказывается соприкасающимся во всех точках кривой L.Образ кривой Lв пространстве E Lназывается развёрткой L'этой кривой на евклидово пространство (для поверхности Fв евклидовом пространстве соприкасающееся евклидово пространство вдоль кривой Lможно интерпретировать как развёрнутую на плоскость огибающую семейства плоскостей, касательных к Fвдоль L) .Вектор (и любой тензор) параллельно переносится вдоль кривой L,если параллельно переносится соответствующий вектор (тензор) в евклидовом пространстве E L,соприкасающемся с римановым вдоль этой кривой. Аналитически параллельное перенесение вектора a i вдоль кривой x i= x i( t) определяется дифференциальным уравнением
Если
Геодезическая кривизна(первая кривизна) кривой Lв точке Моценивает её отклонение от геодезической L 0,касающейся Lв точке М,и определяется следующим образом. Пусть касательный вектор к Lв точке Мпараллельно перенесён в точку M'и образует там угол j с касательной к Lв точке М,пусть s- длина дуги MM'кривой L.При стремлении M'к Мсуществует предел
который и называется геодезической кривизной кривой Lв точке М.Аналитически геодезическая кривизна кривой x I= x i( s), параметризованной длиной дуги, определяется формулами:
где
таким образом, геодезическая кривизна кривой Lсовпадает с (первой) кривизной её развёртки L,а геодезические линии во всех точках имеют нулевую геодезическую кривизну. Для кривой Lв римановом пространстве Rопределяются также вторая и т.д. кривизны и имеют место соотношения, аналогичные обычным формулам Френе (см. Дифференциальная геометрия) для кривых евклидова пространства.
Риманова кривизна.Пусть
М -точка риманова пространства,
F -двумерная поверхность
x
i=
x
i(
u,u)
,проходящая через
М, L -простой замкнутый контур на
F,проходящий через
М,s
-площадь участка поверхности, ограниченного контуром
L.Пусть произвольный вектор
a
i,касательный к поверхности
F(т. е. линейно выражающийся через векторы
Тогда составляющая перенесённого вектора, касательная к F,окажется повёрнутой по отношению к a iна угол j (положительное направление отсчёта углов должно совпадать с направлением обхода L). При стягивании Lв точку Мсуществует предел
называется кривизной риманова пространства (римановой кривизной) в данной точке в направлении двумерной поверхности;
Кзависит не от поверхности, а лишь от её направления в точке
М,т. е. от направления двумерной плоскости касательного евклидова пространства, содержащей векторы
Риманова кривизна Ксвязана с тензором кривизны формулой:
где
причём параметры
u,u выбраны так, что площадь параллелограмма, построенного на векторах
В двумерном случае Ксовпадает с полной кривизной (Theorema egregium К. Ф. Гаусса, 1827), при этом для области G, ограниченной простой замкнутой кривой Г, имеющей геодезическую кривизну k, справедлива так называемая формула Гаусса-Бонне:
в частности, для треугольника, образованного отрезками геодезических
где А, В, С- величины углов треугольника. Для замкнутого (т. е. без границы) двумерного риманова пространства Rего эйлерова характеристика c( R) пропорциональна интегралу римановой кривизны:
Эта формула обобщена на случай чётно-мерного замкнутого риманова пространства, в котором интегрируется некоторая функция компонент тензора кривизны. Если в каждой точке риманова пространства кривизна не зависит от направления двумерной поверхности, то она не меняется и от точки к точке, т. е. пространство имеет постоянную кривизну. Представляют интерес также (в частности, для описания механических систем с циклическими координатами) римановы пространства со специальной структурой тензора кривизны; они суть обобщение пространств постоянной кривизны и имеют достаточно обширную группу движений. Таковы, например, симметрические пространства, характеризующиеся тем, что их тензор кривизны не меняется при параллельном перенесении, субпроективные пространства, характеризующиеся специальной координатной системой, в которой геодезические описываются линейными уравнениями, и др. Риманова кривизна играет важную роль в геометрических приложениях Р. г., тем более, что на всяком многообразии можно ввести некоторую риманову метрику. Так, например, топологическое строение полных римановых пространств (т. е. пространств, в которых всякая геодезическая бесконечно продолжаема) зависит от свойств его кривизны: всякое полное односвязное
n-мерное риманово пространство гомеоморфно
n-мерному евклидову пространству, если его кривизна во всех точках и по всем направлениям неположительна и гомеоморфна
n-мерной сфере единичного радиуса, если его кривизна
Кудовлетворяет неравенствам
Метрическая связность.Параллельное перенесение вдоль кривой
Lс концами
А, Взадаёт изометричное (т. е. сохраняющее расстояния) преобразование t
iкасательного пространства
E
Aв точке
Ав касательное пространство
E
Bв точке
А.Дифференциал преобразования t
iв точке
А,т
.е. главная линейная часть изменения t
i; при переходе из
А(
xi)
в близкую точку
Однако в римановом пространстве
Rможно определить и другие связности, такие, что ассоциированные с ними параллельные перенесения также сохраняют метрический тензор; они называются метрическими связностями и определяются аналогичными коэффициентами
геометрический смысл которого иллюстрируется следующим образом. Рассмотрим в двумерном римановом пространстве метрической связности малый треугольник, образованный отрезками геодезических длины а, b, си углами А, В, С.Тогда главная часть проекции кручения в точке Ана сторону ABравна отношению величины с - acosB - bcosAк площади треугольника, а главная часть проекции кручения на перпендикуляр к AB -величине asinB - bsinA,деленной на площадь треугольника. Т. о., в римановом пространстве нулевого кручения имеют место теоремы косинусов и синусов обыкновенной тригонометрии с точностью до величин, малых в сравнении с площадью треугольника. Кривые, касательный вектор к которым переносится вдоль них параллельно, называются геодезическими соответствующей связности; они совпадают с римановыми геодезическими, если тензор
кососимметричен по всем индексам.
Подпространства.На
m-мерном подмногообразии
Мриманова пространства
R,задаваемом уравнениями
x
i=
x
i(
u
1,..., u
m)
,причём ранг матрицы
Мназывается римановым подпространством пространства R.
Достаточно малая область
m-мерного риманова пространства
Rможет быть погружена в евклидово пространство достаточно большой размерности
N(т. е. допускает сохраняющее длины отображение на подмногообразие этого пространства). Известно, что
Наиболее подробно исследованы погружения двумерных римановых пространств. Так, например: 1) двумерное полное риманово пространство положительной кривизны К.погружается в виде замкнутой выпуклой поверхности (овалоида) в трёхмерное риманово пространство кривизны не меньшей К[проблема Г. Вейля (1916), решенная немецким математиком Х. Леви (1937) и А. Д. Александровым (1941) для погружения в евклидово пространство и А. В. Погореловым (1957) для риманова пространства], причём любые два погружения, имеющие общую точку и общее соприкасающееся пространство в ней, совпадают [т. е. овалоид однозначно определён своей метрикой, немецкий математик С. Э. Кон-Фоссен (1927), А. В. Погорелов (1948)]. 2) Двумерное полное риманово пространство отрицательной кривизны KЈ K o< 0 не допускает погружения в виде регулярной поверхности [советский математик Н. В. Ефимов (1963), частный случай плоскости Лобачевского ( К= -1) разобран Д. Гильбертом (1901)]. 3) Двумерное риманово пространство, гомеоморфное тору, допускает погружение в четырёхмерное евклидово пространство [советский математик Э. Г. Позняк (1973)]. Приложения и обобщения римановой геометрии.1) Поскольку Р. г. определяется заданием дважды ковариантного симметричного тензора, постольку всякую физическую задачу, сводящуюся к изучению такого тензорного поля, можно формулировать как задачу Р. г. В частности, к тензорным полям такого типа относятся различные физические величины, характеризующие упругие, оптические, термодинамические, диэлектрические, пьезомагнитные и другие свойства анизотропных тел. При этом симметрия коэффициентов g ijявляется отражением одного из фундаментальных физических законов - закона взаимности. Так, задача о теплопроводности анизотропного тела, решенная ещё Риманом (1861), явилась первым приложением Р. г. 2) Рассмотрение конфигурационного пространства в механике системы с nстепенями свободы позволило представить в ясной геометрической форме ряд механических задач. Так, например, траектории свободного (т. е. в отсутствии обобщённых сил) движения голономной механической системы с кинетической энергией
где
3) В приложениях Р. г. к механике и физике важную роль играют дополнительные структуры, согласующиеся в том или ином смысле с метрикой риманова пространства. Так, например: а) Физическим представлениям об упругой сплошной среде с непрерывным распределением источников внутренних напряжений соответствует риманово пространство с некоторой метрической связностью: параллельное перенесение, соответствующее ей, определяет так называемое естественное состояние среды вдоль кривой, а кручение отождествляется с плотностью дислокации;
б) римановы пространства с почти комплексной структурой (определяется полем один раз ковариантного и один раз контравариантного тензора
где
в) привлечение понятия так называемой конформной связности, т. е. связности риманова пространства, при которой результат параллельного перенесения метрического тензора g ijпропорционален ему самому, позволило смоделировать некоторые из так называемых Бора постулатов,в частности избранные (или «разрешенные») орбиты движения электронов в атоме - кривые, вдоль которых метрический тензор сохраняется. 4) Развитие Р. г. в связи с общей теорией относительности (см. Тяготение ) и механикой сплошных сред породило различные обобщения её предмета, главнейшими из которых являются так называемые псевдоримановы пространства. Таково, например, согласно теории тяготения, многообразие событий (многообразие пространства - времени) - четырёхмерное пространство с заданной на нём знаконеопределённой невырожденной квадратичной формой
(коэффициенты такой «метрики», допускающей мнимые расстояния, как раз и характеризуют поле тяготения, играя роль потенциальных функций). Эта форма в каждой точке пространства событий может быть приведена к виду ds 2= dx 2+ dy 2+ dz 2 - dt 2 где х, у, z -пространственные координаты, t -время. Физически такие, так называемые локально галилеевы, системы отсчёта являются свободно падающими в поле тяготения. Однако ввести такую систему на всём многообразии невозможно (поскольку наличие поля тяготения математически выражается в кривизне псевдориманова пространства). Другой путь обобщения Р. г. связан с рассмотрением более общих законов определения расстояний, задаваемых в виде линейного элемента ds(см. Финслерова геометрия ) ,и более общих законов параллельного перенесения,а также с отказом от требований регулярности. Лит.:Риман Б., Соч., пер. с нем., М. - Л., 1948; Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; Эйзенхарт Л. П., Риманова геометрия, пер. с англ., М., 1948; Схоутен Я. А., Тензорный анализ для физиков, пер. с англ., М., 1965; Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971. А. Д. Александров, Ю. Ф. Борисов. Риманова поверхность Ри'манова пове'рхность,одно из основных понятий теории функций комплексного переменного. Р. п. введена Б. Риманом (1851) с целью заменить изучение многозначных аналитических функций изучением однозначных аналитических функций точки на соответствующих Р. п. См. Аналитические функции. Риманово пространство Ри'маново простра'нство,пространство, в малых областях которого имеет место приближённо (с точностью до малых высшего порядка сравнительно с размерами областей) евклидова геометрия, хотя точно такое пространство может не быть евклидовым. Р. п. названы по имени Б. Римана,наметившего в 1854 основы теории таких пространств (см. Риманова геометрия ) .Простейшими Р. п. являются евклидово пространство и примыкающие к нему два других пространства постоянной кривизны, в которых имеет место Лобачевского геометрия и Римана геометрия (не смешивать последнюю с общей римановой геометрией, которая изучает Р. п. вообще). Рименшнейдер Тильман Ри'меншнейдер(Riemenschneider) Тильман (около 1460, Хейлигенштадт, Тюрингия, - 7.7.1531, Вюрцбург), немецкий скульптор эпохи Возрождения. Работал в Вюрцбурге (с 1483). В 1525 за связь с восставшими франконскими крестьянами был брошен в тюрьму и подвергнут пыткам. Произведения Р. (статуи Адама и Евы; надгробие Рудольфа фон Шеренберг, камень, 1496-99, собор Санкт-Килиан, Вюрцбург; алтарь святой крови, дерево, 1501-04, Якобскирхе, Ротенбург) сохраняют динамику форм и изломанность линий, характерную для поздней готики.Однако Р. одним из первых отказался от традиционной раскраски и позолоты статуй, наделял отчётливо индивидуализированные персонажи интенсивной духовной жизнью, виртуозно используя для этого фактуру материала и обращая особое внимание на жизненную убедительность мимики и жестов. В поздних работах Р. (алтарь Марии, дерево, 1505-10, Херготскирхе, Креглинген; надгробие Лоренца фон Бибра, камень, около 1519, собор Санкт-Килиан, Вюрцбург; рельеф «Оплакивание Христа» в алтаре приходской церкви в Майдбронне, известняк, 1519-1523) проявляется стремление мастера к большей обобщенности и внутренней ясности образов, к гармонической уравновешенности композиции. Лит.:Flesche Н., Tilman Riemenschneider. [Album], Dresden, [1957]; Gerstenberg K., Tilman Riemenschneider, 5 Aufl., Mьnch., [1962]. В. Д. Синюков. 
Т. Рименшнейдер. Статуя Евы. Камень. 1491-93. Майнско-Франконский музей. Вюрцбург. 
Т. Рименшнейдер. «Св. Симон» (из Мариенкапелле в Вюрцбурге). Дерево. Около 1500. Баварский национальный музей. Мюнхен. 
Т. Рименшнейдер. Статуя Адама. Камень. 1491-93. Майнско-Франконский музей. Вюрцбург. Римини Ри'мини(Rimini), город в Северной Италии, в области Эмилия-Романья, в провинции Форли. Расположен близ берега Адриатического моря, с которым соединён каналом. 119,5 тыс. жителей (1971). Транспортный узел. Металлообрабатывающая, деревообрабатывающая, швейная, пищевая, фармацевтическая промышленность, производство стройматериалов. Рыболовство. Крупный аэропорт; морской порт Р. обслуживает государство Сан-Марино. Римо Римо', долинный ледник в Каракоруме, в истоках р. Раскемдарья (бассейн р. Тарим). Длина 45 км,площадь 510 км 2, высота фирновой линии 5800-6000 м.Имеет дендритовое строение, спускается двумя языками до высоты 5000-5300 м. Римская курия Ри'мская ку'рия,принятое в литературе название совокупности учреждений, подчинённых папе римскому как главе католической церкви и государства Ватикан.Впервые эта система возникла в 12 в. на базе различных учреждений папского двора. Р. к. включает разные конгрегации (церковные министерства), высшие церковные суды и канцелярии, в том числе, например, государственный секретариат, функции которого сходны с функциями министерств иностранных дел буржуазных государств. Римская республика 1798-99 Ри'мская респу'блика 1798-99,провозглашена 15 февраля 1798 римскими республиканцами при поддержке вступившей в город французской армии. Светская власть папы Пия VII в Папской области была ликвидирована. Конституция Р. р. (1798) разработана по образцу французской конституции 1795. В политической жизни Р. р. большую роль играли якобинские демократические элементы. Был принят ряд прогрессивных законов: о конфискации церковных имуществ и их распродаже, о ликвидации ряда феодальных привилегий, об отмене личной зависимости крестьян и пр. Однако фактическое управление страной находилось в руках французской военной администрации. Крайне тяжёлое экономическое положение Р. р. усугублялось систематическим разграблением страны Францией. Контрреволюционные мятежи вспыхнули в различных районах Р. р. Летом 1799 на территорию Р. р. вторглись с С. австрийские, с Ю. - неаполитанские войска. 30 сентября Рим был занят неаполитанцами; в город вступил также отряд русской морской пехоты (800 чел.). Папская власть была восстановлена. Римская республика 1849 Ри'мская респу'блика 1849,провозглашена в Папской области в период Революции 1848-49 в Италии.По характеру проведённых мероприятий была буржуазно-демократической. Руководящую роль в Р. р. играли Дж. Мадзини и Дж. Гарибальди.Р. р. пала под ударами иностранных (главным образом французских) интервентов. Римские провинции Ри'мские прови'нции(лат. provinciae), подвластные Риму территории (вне Италии), управлявшиеся римскими наместниками ( проконсулами или пропреторами), олицетворявшими высшую военную, административную и судебную власть Рима. Первые Р. п. - острова Сицилия (с 241 до н. э.), Сардиния и Корсика (с 227 до н. э.); к концу периода республики насчитывалось около 20 Р. п., в период империи - около 50. В эпоху республики Р. п. рассматривались как «поместья римского народа», значительная часть земли отторгалась у местного населения и передавалась римским колонистам, жители Р. п. были обязаны содержать римских наместников и войско; публиканы,получавшие с торгов на откуп сбор налогов в провинциях, бесконтрольно разоряли местное население; проводилась насильственная романизация. Римское господство вызывало протесты в провинциях, выливавшиеся в восстания ( лузитан,кельтиберов и других испанских племён во 2-1вв. до н. э., Бар-Кохбы в Иудее и др.). Основы провинциальной политики империи были заложены Ю. Цезарем, привлекавшим провинциальную верхушку раздачей целым общинам и отдельным лицам прав римского или латинского гражданства, введением их в сенат, проведением закона (59 до н. э.) против вымогательств в Р. п. и др. Фактически со времени Августа (с конца 1 в. до н. э.) все провинции становились всё более подконтрольными императору, несмотря на их формальное разделение (27 до н. э.) на сенатские и императорские. Постепенный процесс нивелирования собственно Италии и Р. п., выражавший интересы рабовладельческой знати всей империи, нашёл отражение в эдикте императора Каракаллы (212 н. э.), по которому все свободные жители империи получили права римского гражданства, и завершился административной реформой императора Диоклетиана (3 в.), по которой вся Римская империя, включая Италию, была поделена на административно-территориальные единицы - провинции (границы которых не совпадали с границами Р. п.). И. Л. Маяк. Римские протоколы 1934 Ри'мские протоко'лы 1934О взаимоотношениях между Италией, Австрией и Венгрией, подписаны 17 марта в Риме главами правительств фашистской Италии (Б. Муссолини), Австрии (Э. Дольфус) и Венгрии (Д. Гёмбёш). Р. п., предусматривавшие укрепление политического и экономического сотрудничества между их участниками, отражали стремление фашистской Италии вовлечь Австрию и Венгрию в орбиту итальянской внешней политики. После заключения в июле 1936 австро-германского договора, фактически обязавшего Австрию подчинить свою политику интересам германского фашизма, и заключения в октябре 1936 итало-германского союза Р. п. утратили своё значение. Римские цифры Ри'мские ци'фры,цифры древних римлян. Система Р. ц. основана на употреблении особых знаков для десятичных разрядов I = 1, Х =10, С = 100, М = 1000 и их половин V = 5, L = 50, D = 500. Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая - перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры. Например, I, Х, С ставятся соответственно перед Х, С, М для обозначения 9, 90, 900 или перед V, L, D для обозначения 4, 40, 400. Например, VI = 5+1 =6, IV = 5 - 1 = 4 (вместо IIII). XIX = 10 + 10 - 1 = 19 (вместо XVIIII), XL = 50 - 10 = 40 (вместо XXXX), XXXIII = 10 + 10 + 10 + 1 + 1 + 1 = 33 и т.д. Выполнение арифметических действий над многозначными числами в этой записи весьма неудобно. Система Р. ц. в настоящее время не применяется, за исключением, в отдельных случаях, обозначения веков (XV век и т.д.), годов н. э. (MCMLXXVII т. д.) и месяцев при указании дат (например, 1. V.1975), порядковых числительных, а также иногда производных (см. Дифференциальное исчисление ) небольших порядков, больших трёх: y IV , y Vи т.д. Лит.см. при статьях Счисление, Цифры. «Римский вопрос» «Ри'мский вопро'с», конфликт между Ватиканом и итальянским государством, возникший в связи с ликвидацией в 1870 Папской области, территория которой в процессе объединения Италии стала частью Итальянского королевства, а в Рим была перенесена (1871) столица Италии. Папа Пий IX отказался признать объединённое итальянское государство и изданный правительством Италии 13 мая 1871 «Закон о гарантиях прерогатив папы и святейшего престола» («Закон о гарантиях»), который должен был регулировать отношения итальянского государства с папством. На протяжении многих лет Ватикан вёл борьбу против итальянского государства, добиваясь восстановления папского государства и светской власти папы. Ватикан рассчитывал добиться этого с помощью крупных европейских держав. Эти надежды оказались тщетными, но в то же время «Р. в.» был использован католическими державами (Францией, Австрией и др.) в своих политических целях. Окончательно конфликт между Ватиканом и итальянским государством был ликвидирован с заключением в 1929 Латеранских соглашений. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 |
|||||||
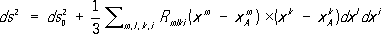 +
+

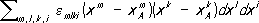 , где
, где
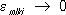 при
при
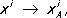
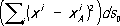 .
.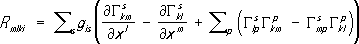
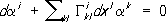 .
.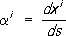 , то получается уравнение геодезических; т. о., геодезические можно определить как кривые, вдоль которых касательный к ним вектор переносится параллельно, т. е. развёртка геодезической - прямая, что углубляет их сходство с прямыми. Результат параллельного перенесения вектора из точки
Ав точку
Взависит, как правило, от кривой
AB,вдоль которой происходит перенесение, - в этом отсутствии «абсолютного параллелизма» наглядно проявляется отличие риманова пространства от евклидова.
, то получается уравнение геодезических; т. о., геодезические можно определить как кривые, вдоль которых касательный к ним вектор переносится параллельно, т. е. развёртка геодезической - прямая, что углубляет их сходство с прямыми. Результат параллельного перенесения вектора из точки
Ав точку
Взависит, как правило, от кривой
AB,вдоль которой происходит перенесение, - в этом отсутствии «абсолютного параллелизма» наглядно проявляется отличие риманова пространства от евклидова.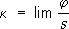 ,
,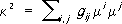 ,
,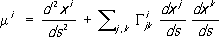 ;
;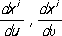 )
,перенесен параллельно по
L.
)
,перенесен параллельно по
L.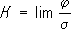 ,
,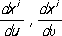 .
.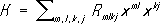 ,
,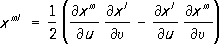 ,
,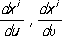 , равна 1.
, равна 1.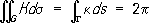 ,
,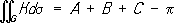 ,
,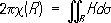 .
.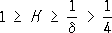 , где d - некоторая постоянная. От величины кривизны полного риманова пространства
Rзависит и его диаметр
d -точная верхняя грань расстояний между точками
R,определяемых внутренней метрикой
R:например, если
К³
K
o
>
0
,то
, где d - некоторая постоянная. От величины кривизны полного риманова пространства
Rзависит и его диаметр
d -точная верхняя грань расстояний между точками
R,определяемых внутренней метрикой
R:например, если
К³
K
o
>
0
,то
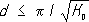 d,если же
d,если же
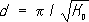 ,то
R -сфера радиуса
,то
R -сфера радиуса
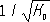 .
.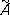 (
x
i+
dx
i)
,определяет некоторый геометрический объект, называется римановой связностью, ассоциированной с данным параллельным перенесением. Аналитически эта связность выражается системой линейных дифференциальных форм
(
x
i+
dx
i)
,определяет некоторый геометрический объект, называется римановой связностью, ассоциированной с данным параллельным перенесением. Аналитически эта связность выражается системой линейных дифференциальных форм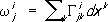 ,
i,
j, …,
n.
,
i,
j, …,
n.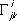 , но уже не симметричными по индексам
j,
kи не выражающимися (подобно символам Кристоффеля) только через тензор
g
ijи его производные. Отличие метрической связности от римановой оценивается так называемым тензором кручения:
, но уже не симметричными по индексам
j,
kи не выражающимися (подобно символам Кристоффеля) только через тензор
g
ijи его производные. Отличие метрической связности от римановой оценивается так называемым тензором кручения: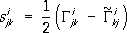 ,
,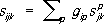
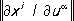 равен
m,имеет место Р. г., определяемая метрическим тензором
равен
m,имеет место Р. г., определяемая метрическим тензором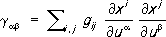
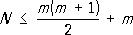 ; вопрос о минимальном значении
Nв общем случае ещё не решен, однако если коэффициенты метрической формы
g
ijпространства
Rявляются аналитическими функциями (т. е. разлагаются в сходящиеся степенные ряды), то
; вопрос о минимальном значении
Nв общем случае ещё не решен, однако если коэффициенты метрической формы
g
ijпространства
Rявляются аналитическими функциями (т. е. разлагаются в сходящиеся степенные ряды), то
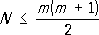 . Относительно задачи погружения в целом (представляющей интерес для физики калибровочных полей) известно ещё меньше.
. Относительно задачи погружения в целом (представляющей интерес для физики калибровочных полей) известно ещё меньше.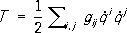
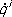 -обобщённые скорости, являются геодезическими соответствующего
n-мерного риманова пространства с метрическим тензором
g
ij.О некоторых других фактах упоминалось выше. Аналогичную интерпретацию получает и движение в поле сил, имеющих потенциал (см.
Герца принцип
)
.
-обобщённые скорости, являются геодезическими соответствующего
n-мерного риманова пространства с метрическим тензором
g
ij.О некоторых других фактах упоминалось выше. Аналогичную интерпретацию получает и движение в поле сил, имеющих потенциал (см.
Герца принцип
)
.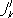 такого, что
такого, что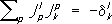
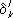 -
Кронекера символ
) используются квантовой механикой для описания наблюдаемых и состояний систем многих частиц;
-
Кронекера символ
) используются квантовой механикой для описания наблюдаемых и состояний систем многих частиц;