 |
|
|
:: Joyce James :: :: :: :: :: :: :: :: :: :: The Boarding House :: :: Windows XP :: :: :: :: :: 3. . . :: Gump & Company :: |
()ModernLib.Net / / / () - (. 40)
Р. в колебательных системах, параметры которых зависят от состояния системы, т. е. в нелинейных системах , имеет более сложный характер, чем в системах линейных. Кривые Р. в нелинейных системах могут стать резко несимметричными, и явление Р. может наблюдаться при различных соотношениях частот воздействия и частот собственных малых колебаний системы (т. н. дробный, кратный и комбинационный Р.). Примером Р. в нелинейных системах может служить т. н. феррорезонанс, т. е. резонанс в электрической цепи, содержащей индуктивность с ферромагнитным сердечником, или ферромагнитный резонанс , представляющий собой явление, связанное с Р. элементарных (атомных) магнитов вещества при приложении высокочастотного магнитного поля (см. Радиоспектроскопия ). Если внешнее воздействие производит периодические изменение энергоёмких параметров колебательной системы (например, ёмкости в электрическом контуре), то при определённых соотношениях частот изменения параметра и собственной частоты свободных колебаний системы возможно параметрическое возбуждение колебаний , или параметрический Р. Р. весьма часто наблюдается в природе и играет огромную роль в технике. Большинство сооружений и машин способны совершать собственные колебания, поэтому периодические внешние воздействия могут вызвать их Р.; например Р. моста под действием периодических толчков при прохождении поезда по стыкам рельсов, Р. фундамента сооружения или самой машины под действием не вполне уравновешенных вращающихся частей машин и т. д. Известны случаи, когда целые корабли входили в Р. при определённых числах оборотов гребного вала. Во всех случаях Р. приводит к резкому увеличению амплитуды вынужденных колебаний всей конструкции и может привести даже к разрушению сооружения. Это вредная роль Р., и для устранения его подбирают свойства системы так, чтобы её нормальные частоты были далеки от возможных частот внешнего воздействия, либо используют в том или ином виде явление антирезонанса (применяют т. н. поглотители колебаний, или успокоители). В др. случаях Р. играет положительную роль, например: в радиотехнике Р. - почти единственный метод, позволяющий отделить сигналы одной (нужной) радиостанции от сигналов всех остальных (мешающих) станций. Лит.:Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 1964; Горелик Г. С., Колебания и волны, Введение в акустику, радиофизику и оптику 2 изд. М., 1959. 
Рис. 1. Механическая колебательная система.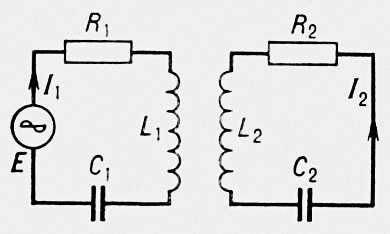 
Рис. 5. Пример двух связанных электрических контуров. 
Рис. 2. Электрическая колебательная система с последовательными включением емкости C и индуктивности L. 
Рис. 4. Электрическая колебательная система с включенными параллельно емкостью и индуктивностью. 
Рис. 6. Резонансная кривая с двумя максимумами. 
Рис. 3. Зависимость амплитуд смещений от частоты внешнего воздействия для различных значений b (b 6< b 5< … < b 1). Резонанса теория Резона'нса тео'рия(в химии), концепция, дополняющая постулаты классической теории химического строения и утверждающая, что если для данного соединения классическая теория (см. Химического строения теория ) допускает построение нескольких приемлемых (согласующихся с требованиями валентности) структурных формул, то действительному состоянию молекул этого соединения отвечает не какая-либо отдельная формула, а некоторое их сочетание (наложение). Р. т. основана на представлениях, сложившихся в химии под влиянием результатов экспериментальных исследований, в которых была обнаружена недостаточность классической теории строения и расхождения этой теории с опытом, а также на идеях одного из квантовомеханических методов расчёта молекул - метода валентных схем, или валентных структур, в котором каждой классической структурной формуле (валентной схеме, или структуре) сопоставляется волновая функция, определённым образом построенная из атомных орбиталей, а волновая функция действительного состояния аппроксимируется линейной комбинацией функций отдельных структур (см. Квантовая химия , Валентность ). Эти представления дополняются в Р. т. критериями отбора наиболее существенных структур среди всех возможных. Так, если в валентной схеме валентный штрих соединяет далеко расположенные друг от друга атомы, то такая схема будет менее значимой, чем та, в которой валентные штрихи соединяют только соседние атомы, и т. п. Для бензола наряду с двумя классическими эквивалентными формулами (структуры Кекуле)
можно записать формулы
(структуры Дьюара), в которых один из валентных штрихов соединяет несоседние атомы. Такие структуры должны играть при описании действительного состояния молекулы бензола меньшую роль, чем структуры Кекуле. Роль тех или иных структур определяется качественными следствиями вариационного принципа квантовой механики: для основного состояния наиболее существенны те структуры, энергия которых минимальна. Чем выше энергия данной структуры по сравнению с минимальной величиной энергии структур, тем менее существенна эта структура для описания молекулы в целом. Согласно вариационному принципу, энергия Е, вычисляемая с оптимальной линейной комбинацией волновых функций структур iменьше энергии E iкаждой отдельной структуры. Минимальное значение разности E i- Еносит название энергии резонанса. Как правило, чем больше значение этой разности, тем больше отклоняется описание состояния реальной молекулы от описания, получаемого в рамках классической теории строения при использовании только одной структурной формулы. На практике обычно пользуются иной величиной, называемой экспериментальной энергией резонанса и определяемой как разность между экспериментальной теплотой образования соединения и энергией, вычисленной для одной структуры, отвечающей классической структурной формуле, при использовании табличных значений энергий отдельных связей. Для описания молекул многих классов соединений достаточно ограничиться одной валентной структурой (например, молекулы насыщенных углеводородов). Для других молекул, например с сопряжённым двойными и тройными связями, приходится использовать представление о наложении (резонансе) нескольких валентных структур. В этих случаях Р. т. прибегает к совокупности структурных формул вместо какой-либо одной формулы, что отличает её от других способов описания, пользующихся пунктирными линиями для валентных штрихов, стрелками для указания смещений электронной плотности и т. п. Отдельные структуры при этом не представляют каких-либо независимых, реально существующих состояний молекулы и являются лишь составными элементами единого описания одного состояния, аналогично тому, как отдельные элементы классического описания (простые связи, двойные связи и т. д.) служат для единого описания структуры молекулы в целом. Р. т. позволяет качественно или полуколичественно (путём простых вычислений на базе упрощённых вариантов метода валентных схем) судить о симметрии молекул, об эквивалентности тех или иных связей и структурных элементов в молекулах, о стабильности и реакционной способности молекул. Она помогает понять, а отчасти и предвидеть результаты экспериментальных исследований, не претендуя на большую строгость рассуждений и не опираясь на достаточно строгие, но громоздкие квантовомеханические расчёты. В рамках Р. т. были введены такие широко используемые в настоящее время представления, как одно- и трёх-электронные связи, гибридизация связевых орбиталей, сверхсопряжение, а также представление о частично ионном характере ковалентных связей между различными атомами (резонанс ковалентной и ионной структур). Р. т. была предложена Л. Полингом в 1928-31 гг. и развита в последующие годы в основном в трудах его школы. Термин «резонанс» был заимствован у В. Гейзенберга , проследившего аналогию между квантовомеханическим описанием систем, например двух связанных осцилляторов, и их классическим описанием, учитывающим резонанс в такой системе. Лит.:Паулинг Л., Природа химической связи, пер. с англ., М. - Л., 1947; Уэланд Д., Теория резонанса и её применение в органической химии, пер. с англ., М., 1948; Полинг Л., Теория резонанса в химии, «Журнал Всесоюзного химического общества им. Д. И. Менделеева», 1962, т. 7, № 4, с. 462; Pauling L., The nature of the chemical bond, 3 ed., lthaca - N. Y., 1960. Резонансная линия Резона'нсная ли'ния,спектральная линия излучения атома, частота которой совпадает с частотой света, поглощаемого им в основном состоянии. Обычно Р. л. называют одну или несколько наиболее интенсивных линий в спектре при резонансном излучении. Резонансное излучение Резона'нсное излуче'ние,излучение, испускаемое системой связанных зарядов (например, атомом, атомным ядром), при котором частота излучения совпадает с частотой возбуждающего света. Р. и. могут испускать газы, жидкости и твёрдые тела, по наиболее чёткая картина наблюдается в атомных парах Hg, Cd, Na и др. Открыто Р. и. было при исследовании свечения паров Na Р. Вудом (1905). Для возбуждения Р. и. атом (или др. систему связанных зарядов) облучают светом частоты n. Поглощая квант с энергией hn ( h - Планка постоянная), атом с основного уровня E 0переходит на возбуждённый уровень E n(уровень E 2на рис .). При спонтанном переходе атома из возбуждённого состояния E nв основное E 0и происходит Р. и. - атом испускает квант с частотой n, и в спектре излучения появляется резонансная линия. Совокупность резонансных линий образует резонансный спектр атома. Р. и. атомов и молекул является резонансной люминесценцией.При взаимодействии атомного ядра с g-излучением может возникать Р. и. g-квантов. Р. и. наблюдается лишь при определённых условиях (в разрежённых атомных парах, замороженных растворах). Обычно атом безызлучательно переходит из возбуждённого состояния в промежуточное (на рис . на уровень E 1), и лишь затем происходит излучательный переход в основное состояние с частотой < n. Если в результате возбуждения атом сразу перешёл на уровень E 1, Р. и. наблюдается в чистом виде (поскольку в этом случае промежуточных уровней нет). Р. и. - процесс, наблюдаемый в течение некоторого времени t.Интенсивность Р. и. Iменяется со временем по закону: I= I 0 e - t/ t ,где I 0 - начальная интенсивность, t - среднее время жизни атома в возбуждённом состоянии. Обычно t @ 10 -8 сек; если электронный переход запрещен отбора правилами , продолжительность Р. и. может значительно увеличиться (например, в парах Hg наблюдается переход с t @ 10 -7 сек). Р. и. всегда поляризовано, причём степень и характер поляризации определяются поляризацией возбуждающего света, направлением наблюдения, излучающим объектом, наличием в нём примесей. Особенно существенно влияет на поляризацию Р. и. магнитное поле (в экспериментах приходится учитывать магнитное поле Земли). В квантовой теории Р. и. (как и в классической теории резонанса ) учитывают эффекты затухания - затухание возбуждённых электронных состояний, которые не являются строго стационарными во времени. Энергия электрона в возбуждённом состоянии не имеет строго определённого значения, и спектральные линии характеризуются некоторой шириной спектральных линий Г. Величина Г связана с полной вероятностью перехода электрона на низшие уровни и с t. Чем больше Г, тем меньше t и, следовательно, меньше длительность Р. и. Лит.:Вуд Р. В., Физическая оптика, пер. с англ., М. - Л. , 1936; Гайтлер В., Квантовая теория излучения, [пер. с англ.], М., 1956; Ахиезер А. И., Берестецкий В. Б., Квантовая электродинамика, 3 изд., М., 1969. В. З. Кресин. Резонансные пиломатериалы
Резона'нсные пиломатериа'лы, вырабатываются из лиственных и хвойных древесных пород, древесина которых обладает способностью усиливать
звук музыкальный,не искажая его тон. Способность к резонансу Р. п. характеризуется акустической константой
С=
Резонансы
Резона'нсы,резонансные частицы, короткоживущие возбуждённые состояния сильно взаимодействующих
элементарных частиц
(адронов). В отличие от др. нестабильных частиц, Р. распадаются в основном за счёт
сильных взаимодействий.Поэтому их времена жизни лежат в интервале 10
-22
-10
-24
сек,
что по порядку величины совпадает с характерным ядерным временем t
яд=
R
яд/
с» 10
-23
сек, где
с -скорость света в вакууме,
R
яд- характерный радиус сильных (ядерных) взаимодействий, примерно равный
комптоновской длине волны
p-мезона,
R
яд
~
В зависимости полных эффективных поперечных сечений рассеяния s от энергии ЕР. часто проявляются в виде колоколообразного (т. н. брейт-вигнеровского) максимума:
(форма которого совпадает, например, с зависимостью квадрата амплитуды колебаний от частоты w в механической системе при изменении w в окрестности резонансной частоты). Энергия Е,соответствующая максимуму сечения s = s 0 ,сопоставляется с массой Р. М(по формуле относительности теорииМ= E 0/ c 2 .В физике элементарных частиц массу принято выражать в энергетических единицах, т. е. считать с= 1; тогда М= E 0) .Величина Г является полной шириной максимума в энергетической шкале. Первый Р. был открыт в начале 50-х гг. Э.
Ферми
с сотрудниками при изучении процесса взаимодействия p
+мезонов с протонами на протонном циклотроне в Чикаго (США). Этот Р. -D
3,
3в современных обозначениях (первая цифра индекса у символа Р. означает удвоенный
изотопический спинIчастицы, вторая - её удвоенный спин
J) - можно представлять себе как возбуждённое состояние
нуклона
(N), в которое последний переходит, поглотив p-мезон (пион). Собственная масса Р. D
3,
3, равная полной энергии системы N + p в системе центра инерции (с. ц. и. ) этих частиц,
М= (1233 ± 3)
Мэв, а время жизни t = 5,7Ч10
-24
сек.Величина, обратная t, определяет вероятность распада частицы. Вместо времени жизни в физике Р. чаще используют полную энергетическую ширину G, которая связана с t соотношением t
В квантовомеханической амплитуде T 3, 3( E) pN-pacceяния в состоянии с I= J= 3/ 2этот Р. проявляется в виде т. н. брейт-вигнеровского вклада
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107 |
|||||||
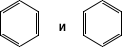
, где
Е -модуль упругости, а r - плотность материала. Лучшими резонансными свойствами обладают
ель
и кавказская
пихта
, несколько уступают им
кедровая сосна
,
явор
,
граб.Р. п. идут главным образом на изготовление
дек
клавишных, щипковых и смычковых музыкальных инструментов.
»
1,4Ч10
-13
см(
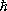- постоянная Планка,
m
p
-масса p-мезона).
(1)
, (вытекающим из
неопределённостей соотношения
для энергии и времени). Р. D
3,
3имеет полную ширину Г = (116 ± 6)
Мэв, спин
J=
3/
2и изотопический спин
I=
3/
2.
, (2)