 |
|
|
|
()ModernLib.Net / / / () - (. 27)
где значения x ji, j= 1, ..., kпредполагаются известными. Эта форма линейной модели регрессии является общей в том смысле, что к ней сводятся модели более высоких порядков по переменным x 1, ..., x k. Кроме того, некоторые нелинейные относительно параметров b i ; модели подходящим преобразованием также сводятся к указанной линейной форме. Р. а. является одним из наиболее распространённых методов обработки результатов наблюдений при изучении зависимостей в физике, биологии, экономике, технике и др. областях. На модели Р. а. основаны такие разделы математической статистики, как дисперсионный анализ и планирование эксперимента ; модели Р. а. широко используются в статистическом анализе многомерном.
Лит.:Юл Дж. Э., Кендэл М. Дж., Теория статистики, пер. с англ., 14 изд., М., 1960; Смирнов Н. В., Дунин-Барковский И. В., Курс теории вероятностей и математической статистики для технических приложений, 3 изд., М., 1969; Айвазян С. А., Статистическое исследование зависимостей, М., 1968; Рао С. Р., Линейные статистические методы и их применения, пер. с англ., М., 1968. См. также лит. при ст. Регрессия . А. В. Прохоров. Регрессия (математич.)
Регре'ссияв теории вероятностей и математической статистике, зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. В отличие от чисто функциональной зависимости
у=
f(
х), когда каждому значению независимой переменной
хсоответствует одно определённое значение величины
у, при регрессионной связи одному и тому же значению
хмогут соответствовать в зависимости от случая различные значения величины
у.Если при каждом значении
х=
x
iнаблюдается
n
i, значений
y
i
1, ...,
Изучение Р. в теории вероятностей основано на том, что случайные величины Хи Y, имеющие совместное распределение вероятностей, связаны вероятностной зависимостью: при каждом фиксированном значении Х= хвеличина Yявляется случайной величиной с определённым (зависящим от значения х) условным распределением вероятностей. Р. величины Yпо величине Хопределяется условным математическим ожиданием Y, вычисленным при условии, что Х= х: Е( Yк х) = u( х). Уравнение у= u( х), в котором хиграет роль «независимой» переменной, называется уравнением регрессии, а соответствующий график - линией регрессии величины Yпо X.Точность, с которой уравнение Р. Yпо Хотражает изменение Yв среднем при изменении х,измеряется условной дисперсией величины Y, вычисленной для каждого значения Х= х: D( Yк х) = s 2( x). Если s 2( х) = 0 при всех значениях х, то можно с достоверностью утверждать, что Yи Хсвязаны строгой функциональной зависимостью Y= u( X) .Если s 2( х) = 0 при всех значениях хи u( х) не зависит от х, то говорят, что Р. Yпо Хотсутствует. Аналогичным образом определяется Р. Хпо Yи в частности, уравнение Р. х= u( у), = Е( Хп Y= у). Функции у= u( х) и х= u( у), вообще говоря, не являются взаимно обратными. Линии Р. обладают следующим замечательным свойством: среди всех действительных функций f( х) минимум математического ожидания Е[ Y- f( X)] 2достигается для функции f( x) = u( х), т. е. Р. Yпо Хдаёт наилучшее, в указанном смысле, представление величины Yпо величине X. Это свойство используется для прогноза Yпо X: если значение Yнепосредственно не наблюдается и эксперимент позволяет регистрировать лишь компоненту Хвектора ( X, Y), то в качестве прогнозируемого значения Yиспользуют величину u( X). Наиболее простым является случай, когда Р. Yпо Хлинейна: Е( Yп x) = b 0+ b 1 x. Коэффициенты b 0и b 1, называются коэффициентами регрессии, определяются равенствами
где
m
Хи
m
Y
-математические ожидания
Хи
Y,
В случае, когда совместное распределение Хи Yнормально, обе линии Р. у= u( х) и х= u( у) являются прямыми. Если Р. Yпо Х отлична от линейной, то последнее уравнение есть линейная аппроксимация истинного уравнения Р.: математическое ожидание Е[ Y- b 0 - b 1 X] 2 достигает минимума b 0и b 1при b 0 = b 0и b 1 = b 1. Особенно часто встречается случай уравнения Р., выражающегося линейной комбинацией тех или иных заданных функций: у= u( Х) =b 0j 0( x) + b 1j 1( x) + ... + b mj m( x). Наиболее важное значение имеет параболическая (полиномиальная) Р., при которой j 0( x) = 1 , j 1( x) = x, ..., j m( x) = x m . Понятие Р. применимо не только к случайным величинам, но и к случайным векторам. В частности, если Y- случайная величина, а Х= ( X 1, ..., X k) -случайный вектор, имеющие совместное распределение вероятностей, то Р. Yпо Xопределяется уравнением y= u( x 1, ..., x k), где u( x 1, ..., x k) = E{ Yп X= x 1, ... , X k = x k}. Если u( x 1, ..., x k) = b 0+ b 1 x 1+ ... + b k x k, то Р. называется линейной. Эта форма уравнения Р. включает в себя многие типы Р. с одной независимой переменной, в частности полиномиальная Р. Yпо Хпорядка kсводится к линейной Р. Yпо X 1, ..., X k, если положить X k = X k . Простым примером Р. Yпо Хявляется зависимость между Yи X, которая выражается соотношением: Y= u( X) + d, где u( x) = Е( YI X= х), а случайные величины Хи d независимы. Это представление полезно, когда планируется эксперимент для изучения функциональной связи у= u( х) между неслучайными величинами уи х. На практике обычно коэффициенты Р. в уравнении у= u( х) неизвестны и их оценивают по экспериментальным данным (см. Регрессионный анализ ). Первоначально термин «Р.» был употреблен английским статистиком Ф. Гальтоном (1886) в теории наследственности в следующем специальном смысле: «возвратом к среднему состоянию» (regression to mediocrity) было названо явление, состоящее в том, что дети тех родителей, рост которых превышает среднее значение на аединиц, имеют в среднем рост, превышающий среднее значение меньше чем на аединиц. Лит.:Крамер Г., Математические методы статистики, пер. с англ., М., 1948; Кендалл М. Дж., Стьюарт А., Статистические выводы и связи, пер. с англ., М., 1973. А. В. Прохоров. Регрессия моря Регре'ссияморя (от лат. regressio - обратное движение, отход), отступание моря от берегов. Происходит в результате поднятия суши, опускания дна океана или уменьшения объёма воды в океанических бассейнах (например, во время ледниковых эпох). Р. происходили многократно в различных районах Земли на протяжении всей её истории. См. также Трансгрессия. Регрессный иск Регре'ссный иск,обратное требование, в гражданском праве и процессе адресованное в суд или арбитраж требование гражданина или организации, исполнивших обязательство за должника либо за какое-либо др. лицо, возместить уплаченную денежную сумму. Например, по советскому праву организация или гражданин, ответственные за причинённый вред, обязаны по Р. и. органа социального страхования или социального обеспечения возместить суммы пособия либо пенсии, которые выплачены потерпевшему в связи с болезнью или увечьем, полученным по их вине, а в случае смерти потерпевшего - лицам, указанным в законе. В соответствии со ст. 81 Основ гражданского законодательства 1961 страховая организация, уплатившая страховое возмещение по имущественному страхованию, вправе предъявить в пределах этой суммы требование к лицу, ответственному за причинённый вред. Ст. 93 Основ законодательства о труде предоставляет суду право возложить на должностное лицо, виновное в незаконном увольнении или переводе работника на др. работу, обязанность возместить ущерб, причинённый организации, оплатившей время вынужденного прогула или выполнения нижеоплачиваемой работы. В арбитражной практике Р. и. применяются в отношениях между предприятиями и др. организациями для переложения суммы, уплаченной организацией-должником за неисполнение или ненадлежащее исполнение договора, на организацию, непосредственно виновную в нарушении договорного обязательства (например, поставившую недоброкачественную, некомплектную продукцию). Регтайм Ре'гтайм(англ. ragtime, от rag - обрывок и time - время, темп, такт), 1) форма городской танцевально-бытовой музыки американских негров, сложившаяся во 2-й половине 19 в. Своеобразная остросинкопированная музыка Р. - одна из предшественниц джаза. Ранние образцы художественного претворения музыкальной формы Р. дал А. Дворжак в симфонии «Из Нового Света» и струнном квартете. 2) Американский салонный и бальный танец, основан на ритмической форме Р. Музыкальный размер 2/ 4. Исполняется парами. Вошёл в моду около 1910. От Р. образовались танцы ту-степ, уан-степ, фокстрот. Особенности Р. использовал И. Ф. Стравинский («Регтайм» для 11 инструментов, Р. в балетной пантомиме «Сказ о беглом солдате и чёрте»). Регул (звезда) Ре'гул(a Льва), звезда 1,4 визуальной звёздной величины , наиболее яркая в созвездии Льва, светимость в 169 раз больше солнечной, расстояние от Солнца 26 пс.Р. представляет собой систему из трёх звёзд. Регул Марк Атилий Ре'гулМарк Атилий (Marcus Atilius Regulus) (умер около 248 до н. э.), римский полководец и политический деятель. Будучи в 267 консулом, завоевал г. Брундизий. В период 1-й Пунической войны, в 256 во время своего второго консульства Р. одержал победу над карфагенянами при мысе Экном и возглавил военные действия римлян в Африке. Им была одержана победа около Клупеи, но весной 255 при Тунесе (около Карфагена) армия Р. была разбита карфагенянами. Р. умер в плену. Регулирование автоматическое Регули'рование автомати'ческое(от нем. regulieren - регулировать, от лат. regula - норма, правило), поддержание постоянства (стабилизация) некоторой регулируемой величины, характеризующей технический процесс, либо её изменение по заданному закону (программное регулирование) или в соответствии с некоторым измеряемым внешним процессом (следящее регулирование), осуществляемое приложением управляющего воздействия к регулирующему органу объекта регулирования; разновидность автоматического управления.При Р. а. управляющее воздействие u( t) обычно является функцией динамической ошибки - отклонения e( t) регулируемой величины х( t) от её заданного значения x 0( t): e( t) = x 0( t) - х( t) (принцип Ползунова - Уатта регулирования по отклонению, или принцип обратной связи ) ( рис. , а). Иногда к Р. а. относят также управление, при котором u( t) вырабатывается (устройством компенсации) в функции возмущающего воздействия f(нагрузки) на объект (принцип Понселе регулирования по возмущению) ( рис. , б), и комбинированное регулирование по отклонению и возмущению ( рис. , б). Для осуществления Р. а. к. объекту подключается комплекс устройств, представляющих собой в совокупности
регулятор.Объект и регулятор образуют систему автоматического регулирования (CAP). САР по отклонению является замкнутой (см.
Замкнутая система управления
),
по возмущению - разомкнутой (см.
Разомкнутая система управления
). Математическое выражение функциональной зависимости желаемого (требуемого) управляющего воздействия
u
0(
t) от измеряемых регулятором величин называется законом, или
алгоритмом
, регулирования. Наиболее часто применяемые законы Р. а.: П - пропорциональный (статический),
u
0=
ke, И - интегральный (астатический),
САР может находиться в состоянии равновесия, в ней могут протекать установившиеся и переходные процессы, количественные характеристики которых изучает теория автоматического регулирования (ТАР). В статических системах регулирования установившаяся погрешность (ошибка ) e стпри постоянной нагрузке (на объект) зависит от величины последней. Для повышения статической точности увеличивают коэффициент усиления регулятора k, но при достижении им некоторого критического значения k kpсистема обычно теряет устойчивость.Введение в регулятор интегрирующих элементов позволяет получить астатическую систему регулирования , в которой при любой постоянной нагрузке статическая ошибка отсутствует. ТАР изучает условия устойчивости, показатели качества процесса регулирования (динамическую и статическую точность, время регулирования, колебательность системы, степень и запасы устойчивости и т. п.) и методы синтеза CAP, т. е. определения структуры и параметров корректирующих устройств, вводимых в регулятор для повышения устойчивости и обеспечения требуемых показателей качества Р. а. Наиболее полно разработана ТАР линейных систем, в которой применяются аналитические и частотные методы исследования. Малые отклонения от равновесных состояний в непрерывных нелинейных системах Р. а. исследуются посредством линеаризации исходных уравнений. Процессы при больших отклонениях и специфических особенности; нелинейных CAP (предельные циклы, автоколебания, захватывание, скользящие режимы и т. п.) изучаются методами фазового пространства.Для изучения периодических режимов также применяют приближённые методы малого параметра, гармония, баланса и др. Устойчивость при больших отклонениях исследуется вторым (прямым) методом Ляпунова и методом абсолютной устойчивости, разработанным : В. М. Поповым (Румыния). Специальный раздел ТАР посвящен Р. а. при случайных воздействиях. С 50-х гг. 20 в. развиваются теория инвариантных CAP, обеспечивающих независимость х( t) от возмущений, и теория многосвязных CAP, в которых многие величины связаны через регулируемый объект. В таких CAP часто вводят дополнительные связи между регуляторами в целях получения определённых свойств, в частности автономности (независимости процессов регулирования отдельных величин). В 60-х гг. получила развитие и применение теория систем с переменной структурой, особенно эффективных при работе в условиях больших изменений параметров системы и среды, т. к. переходные процессы в них определяются свойствами управляющего устройства и мало зависят от параметров объекта регулирования и среды. Особое место в ТАР занимают дискретные системы Р. а., в которых осуществляется квантование сигнала.Из них наиболее изучены импульсные системы (с квантованием по времени), релейные системы (с квантованием по уровню) и цифровые системы (с квантованием по времени и уровню). Частный вид релейных систем - двухпозиционные регуляторы , в которых регулирующий орган может занимать лишь одно из двух крайних положений. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107 |
|||||||
величины
у, то зависимость средних арифметических
от
x
iи является Р. в статистическом понимании этого термина. Примером такого рода зависимости служит, в частности, зависимость средних диаметров сосен от их высот; см. табл. в ст.
Корреляция
.
,
и
- дисперсии
Хи
Y, а r - коэффициент корреляции между
Хи
Y. Уравнение Р. при этом выражается формулой
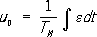; ПИ - пропорционально-интегральный (изодромный),
, ПИД - пропорционально-интегральный с производной,
; здесь
k -коэффициет усиления регулятора,
Т
ии
Т
д-
постоянные времени
интегрирования и дифференцирования. Фактическое воздействие
u(
t) отличается от
u
0(
t)
вследствие инерционности регулятора. CAP является
динамической системой
,
процессы в которой описываются дифференциальными, дифференциально-разностными и т. п. уравнениями.