Равновеликая проекция

Равновели'кая прое'кция,эквивалентная проекция, одна из .

Равновеликие и равносоставленные фигуры

Равновели'кие и равнососта'вленные фигу'ры.Равновеликие фигуры - плоские (пространственные) фигуры одинаковой площади (объёма); равносоставленные фигуры - фигуры, которые можно разрезать на одинаковое число соответственно конгруэнтных (равных) частей. Обычно понятие равносоставленности применяется только к многоугольникам и многогранникам. Равносоставленные фигуры являются равновеликими. Венгерский математик Я. Больяй (1832) и немецкий математик П. Гервин (1833) доказали, что равновеликие многоугольники являются равносоставленными (теорема Больяй - Гервина). Поэтому разрезанием на части и перекладыванием их можно любой многоугольник превратить в равновеликий ему квадрат. Понятие равносоставленности лежит в основе «метода разбиения», применяемого для вычисления площадей многоугольников: параллелограмм «разрезанием и перекладыванием» сводят к прямоугольнику, треугольник - к параллелограмму, трапецию - к треугольнику. Эквивалентным понятию равносоставленности является понятие равнодополняемости, которое лежит в основе «метода дополнения», т. е. дополнения двух фигур равными частями так, чтобы получившиеся после такого дополнения фигуры были равны.

  Равновеликие многогранники не всегда являются равносоставленными. (Поэтому при выводах формулы объёма треугольной пирамиды используют или иное завуалированное интегрирование, например .См. также .) Так, например, куб и равновеликий ему правильный тетраэдр не являются равносоставленными - т. н. теорема Дена, доказанная немецким математиком М. Деном (1901) и составившая отрицательное решение третьей проблемы Гильберта. Для доказательства Ден построил некоторую систему аддитивных инвариантов, равенство которых необходимо для равносоставленности многогранников, и убедился, что среди его инвариантов есть такие, которые принимают разные значения для куба и равновеликого ему правильного тетраэдра. Эти работы были продолжены швейцарским математиком Х. Хадвигером и его учениками; в частности, Ж. П. Зидлер установил, что совпадение инвариантов Дена двух многогранников не только необходимо, но и достаточно для их равносоставленности.

  Лит.:Проблемы Гильберта. Сб., М., 1969; Болтянский В. Г., Равновеликие и равносоставленные фигуры, М., 1956; Энциклопедия элементарной математики, книга 5, М., 1966.

  В. Г. Болтянский.

Равновесие механической системы

Равнове'сие механи'ческой систе'мы,состояние механической системы, находящейся под действием сил, при котором все её точки покоятся по отношению к рассматриваемой системе отсчёта. Если система отсчёта является инерциальной (см. ), равновесие называется абсолютным, в противном случае - относительным. Изучение условий Р. м. с. - одна из основных задач .Условия Р. м. с. имеют вид равенств, связывающих действующие силы и параметры, определяющие положение системы; число этих условий равно числу степеней свободы системы. Условия относительности Р. м. с. составляются так же, как и условия абсолютного равновесия, если к действующим на точки силам прибавить соответствующие переносные .Условия равновесия свободного твёрдого тела состоят в равенстве нулю сумм проекций на три координатные оси Oxyzи сумм моментов относительно этих осей всех приложенных к телу сил, т. е.

При выполнении условий (1) тело будет по отношению к данной системе отсчёта находиться в покое, если скорости всех его точек относительно этой системы в момент начала действия сил были равны нулю. В противном случае тело при выполнении условий (1) будет совершать т. н. движение по инерции, например двигаться поступательно, равномерно и прямолинейно. Если твёрдое тело не является свободным (см. ), то условия его равновесия дают те из равенств (1) (или их следствий), которые не содержат реакций наложенных связей; остальные равенства дают уравнения для определения неизвестных реакций. Например, для тела, имеющего неподвижную ось вращения Oz,условием равновесия будет е m _z( F _k) = 0; остальные равенства (1) служат для определения реакций подшипников, закрепляющих ось. Если тело закреплено наложенными связями жестко, то все равенства (1) дают уравнения для определённой реакции связей. Такого рода задачи часто решаются в технике.

  На основании равенства (1), не содержащие реакций внешних связей, дают одновременно необходимые (но недостаточные) условия равновесия любой механической системы и, в частности, деформируемого тела. Необходимые и достаточные условия равновесия любой механической системы могут быть найдены с помощью .Для системы, имеющей sстепеней свободы, эти условия состоят в равенстве нулю соответствующих обобщённых сил:

Q ₁ = 0, Q ₂ = 0, ЧЧЧ, Q _s = 0.     (2)

  Из состояний равновесия, определяемых условиями (1) и (2), практически реализуются лишь те, которые являются устойчивыми (см. ). Равновесия жидкостей и газов рассматриваются в и .

  С. М. Тарг.

Равновесие статистическое

Равнове'сие статисти'ческое,состояние замкнутой статистической системы, в которой среднее значения всех физических величин, характеризующих состояние, не зависят от времени. Р. с. - одно из основных понятий ,играющее такую же роль, как в термодинамике. Р. с. не является равновесным в механическом смысле, т.к. в системе при этом не прекращаются малые .Теория Р. с. даётся в статистической физике, которая описывает его с помощью различных (микроканонического, канонического или большого канонического) в зависимости от типа контакта системы с окружающей средой.

Равновесие термодинамическое

Равнове'сие термодинами'ческое,состояние термодинамической системы, в которое она самопроизвольно приходит через достаточно большой промежуток времени в условиях изоляции от окружающей среды, после чего параметры состояния системы уже не меняются со временем. Изоляция не исключает возможности определённого типа контактов со средой (например, теплового контакта с , обмена веществом и др.). Процесс перехода системы в равновесное состояние называемое .При Р. т. в системе прекращаются все , связанные с , - теплопроводность, диффузия, химические реакции и т.д. Равновесное состояние системы определяется значениями её внешних параметров (объёма, напряжённости электрического или магнитного поля и др.), а также значением .Строго говоря, параметры состояния равновесной системы не являются абсолютно фиксированными - в микрообъёмах они могут испытывать малые колебания около своих средних значений ( ).

 Изоляция системы осуществляется в общем случае при помощи неподвижных стенок, непроницаемых для вещества. В случае, когда изолирующие систему неподвижные стенки практически не теплопроводны (например, в ), имеет место адиабатическая изоляция, при которой энергия системы остаётся неизменной. При теплопроводящих (диатермических) стенках между системой и внешней средой, пока не установилось равновесие, возможен . При длительном тепловом контакте такой системы с внешней средой, обладающей очень большой теплоёмкостью (термостатом), температуры системы и среды выравниваются и наступает Р. т. При полупроницаемых для вещества стенках Р. т. наступает в том случае, если в результате обмена веществом между системой и внешней средой выравниваются среды и системы.

  Одним из условий Р. т. является механическое равновесие, при котором невозможны никакие макроскопические движения частей системы, но поступательное движение и вращение системы как целого допустимы При отсутствии внешних полей и вращения системы условием её механического равновесия является постоянство давления во всём объёме системы. Другие необходимые условия Р. т. - постоянство температуры и химического потенциала в объёме системы. Достаточные условия Р. т. (условия устойчивости) могут быть получены из (принципа максимальной ); к ним, например, относятся: возрастание давления при уменьшении объёма (при постоянной температуре) и положительное значение теплоёмкости при постоянном давлении. В общем случае система находится в Р. т. тогда, когда термодинамический потенциал системы, соответствующий независимым в условиях опыта переменным, минимален. Например, при заданных объёме и температуре должна быть минимальна , а при заданных давлении и температуре - термодинамический потенциал Гиббса (см. ).

  Лит.:Кубо Р., Термодинамика, пер. с англ., М. ,1970; Самойлович А. Г., Термодинамика и статистическая физика, 2 изд., М., 1955; Ван-дер-Ваальс И. Д., Констамм Ф., Курс термостатики, ч. 1 - Общая термостатика, пер, с англ., М., 1936.

  Д. Н. Зубарев.

Равновесие химическое

Равнове'сие хими'ческое,состояние системы, в которой обратимо протекает одна или несколько , причём для каждой из них скорости прямой и обратной реакций равны, вследствие чего состав системы остаётся постоянным, пока сохраняются условия её существования. В простейшем случае, когда система гомогенна и в ней протекает обратимая химическая реакция

А + В Ы С + D,

скорость прямой реакции пропорциональна реагирующих веществ

u ₁= k ₁[A][B],

а скорость обратной реакции пропорциональна концентрациям продуктов реакции

u ₂ = k ₂[C][D],

где k ₁и k ₂- соответствующие константы скоростей при данных условиях. В начальный момент, когда [С] и [D] равны нулю, u ₂= 0, a u ₁определяется начальными концентрациями А и В. По мере расходования этих веществ и образования веществ С и D u ₁уменьшается, a u ₂ возрастает, затем они становятся равными (u ₁= u ₂), т. е. устанавливается Р. х. Из равенства u ₁= u ₂следует, что

'

где [С], [D], [А] и [В] - равновесные концентрации реагентов, а К -константа равновесия, зависящая для каждой обратимой реакции от внешних условий. Полученное соотношение есть выражение ; оно характеризует тот предел, до которого может меняться исходный состав системы при самопроизвольном течении реакции в данных условиях, т. е. без затраты работы извне. В условиях Р. х. концентрации ( ) всех реагентов связаны между собой и нельзя изменить ни одной из них без того, чтобы не изменились все остальные. Приведённое выражение для Ксправедливо в случае газовых реакций при невысоких давлениях и в разбавленных растворах.

  Термодинамически Р. х. - и в гомогенных, и в гетерогенных системах - характеризуется как состояние, наиболее устойчивое в данных условиях, т. е. такое, в котором (в зависимости от способа задания внешних условий) та или иная термодинамическая функция состояния (см. ) достигает своего минимального или максимального значения. Для изолированных систем, т. е. не обменивающихся веществом и энергией с внешней средой, такой функцией является .При Р. х. энтропия системы максимальна. Если возможен теплообмен с окружающей средой, но температура и давление в системе постоянны, то минимальное значение принимает изобарно-изотермический потенциал (см. ). При постоянстве температуры и объёма минимума достигает изохорно-изотермический потенциал (см. ).

 Зависимость Р. х. от внешних условий в качественной форме выражается , в количественной - соответствующими термодинамическими уравнениями. Так, влияние температуры выражается уравнениями или реакции.

  Изучение Р. х. имеет большое теоретическое и практическое значение, особенно возросшее в связи с проведением процессов в сложных многокомпонентных системах. Большие трудности исследования химических реакций при высоких температурах (высокотемпературная химия) экспериментальными методами вызвали интенсивное развитие расчётов равновесных составов смесей при заданных начальных внешних условиях и исходных концентрациях (или количествах) компонентов. В химической технологии определение положения Р. х. при различных давлениях и температурах и учёт скоростей реакций позволяют выбирать оптимальные условия процесса, в частности условия максимального выхода химических продуктов. Большое значение приобрёл расчёт начального состава смеси по заданному, а также состава квазиравновесных систем, в которых одна или несколько термодинамически возможных реакций практически не осуществляются или в силу своих кинетических особенностей идут очень медленно.

  Лит.:Курс физической химии, под общ. ред. Я. И. Герасимова, 2 изд., т. 1, М., 1969; Термодинамические и теплофизические свойства продуктов сгорания. Справочник, т. 1, М., 1971.

  М. Е. Ерлыкина.

Равновесия органы

Равнове'сия о'рганы,органы животных и человека, воспринимающие изменения положения тела в пространстве, а также действия на организм ускорений и изменений гравитационных сил. У беспозвоночных Р. о. представлены , или слуховыми пузырьками, имеющими различное строение и местоположение. У большинства беспозвоночных - это впячивания ,которые сообщаются с наружной средой при помощи канала или отшнуровываются, образуя замкнутый пузырёк. Внутри статоцистов расположены особые твёрдые образования - .Внутренняя полость статоциста, как правило, выстлана чувствующими клетками, снабженными ресничками. Обычно статолит имеет большую плотность, чем окружающая его жидкость, и поддерживается чувствительными волосками. Если статолит окружен чувствительными волосками со всех сторон, то при любом изменении положения тела животного в пространстве будут раздражаться смещенным статолитом соответствующие группы волосков. Волосковые клетки ракообразных представляют собой первичные чувствующие .Статоцисты медуз и морских ежей - маленькие колбовидные выпячивания наружных покровов тела, внутри которых также находятся статолиты. Но в этом случае реснитчатые клетки расположены снаружи статоциста среди эпителиальных клеток, окружающих его, либо в наружной стенке самого статоциста. У сцифоидных кишечнополостных имеется 8 статоцистов, расположенных радиально по краю .У насекомых не обнаружено настоящих статоцистов. У некоторых водяных клопов и гладыша роль статоцистов выполняют покрытые чувствительными волосками наружные участки тела, удерживающие воздушные пузырьки (т. н. газовый статолит). Наиболее сложно устроены Р. о. головоногих моллюсков: статоцисты в виде пузырьков помещаются у них в капсуле головного хряща; однако даже у осьминога их удаление вызывает лишь незначительные нарушения в способности к ориентации. Возбуждение чувствующих клеток статоцистов передаётся в центральные отделы нервной системы. Механизмы ответных реакций животных, лишённых нервной системы, менее ясны. Многие равновесия дают сигналы двух типов - статические, связанные с положением тела, и динамические, связанные с ускорением.

  Р. о. позвоночных и человека представлены , рецепторная часть которого расположена во (см. также ). Поступающие из рецепторов равновесия сигналы, связанные с положением тела или с ускорением, возникают при механическом раздражении чувствительных волосков смещенными , купулами или эндолимфой. Возникающие импульсы передаются по вестибулярному нерву в мозг. Сложная организация центральных вестибулярных механизмов, их многочисленные связи с и обеспечивают функциональную взаимосвязь с др. . Тесное взаимодействие между центральными вестибулярными и нервными механизмами, осуществляющими глубокое , обусловливает тонкую регуляцию тонуса мышц. Совокупность сенсорных сигналов от лабиринтов, глаз, мышечных, суставных и кожных рецепторов вызывает статокинетические рефлексы, вследствие которых животное и человек поддерживают нормальную ориентацию по отношению к направлению силы тяжести и противодействуют ускорениям во всех плоскостях. Эти рефлекторные реакции протекают при участии спинного мозга и нижних отделов головного мозга. См. также , .

 Нарушения равновесия у человека наблюдаются при ряде заболеваний нервной системы (см. ), а также при раздражении и болезнях вестибулярного аппарата (см. , , ).

  Лит.см. при ст. , .

  Г. Н. Симкин.

Равновесия теория

Равнове'сия тео'рия,название ряда немарксистских социально-исторических концепций, которые пытаются объяснить процессы развития и функционирования общества или его элементов на основе принципа равновесия, заимствованного из естествознания. Эти концепции не представляют собой теорий в строгом смысле слова: понятие равновесия используется здесь именно в качестве общего объяснительного принципа.

  Попытки рассмотреть общество как равновесную систему впервые возникают в европейской социальной науке в 17 в. под влиянием бурно развивавшегося механистического естествознания (Б. Спиноза, Т. Гоббс, Г. Лейбниц). Рассматривая социальные проблемы с позиций «социальной физики», «механики страстей», мыслители той эпохи были склонны проблему общественного порядка сводить к существованию равновесия между частями общества, напоминающего равновесие элементов физического мира. Собственно Р. т. впервые получила развёрнутое изложение в 18 в. в утопических построениях Ш. , который на «открытых» им способах расчёта равновесия и гармонизации страстей основывал свой план идеального человеческого общежития, а идею равновесия считал универсальной для всего мироздания.

  Во 2-й половине 19 в. идею равновесия применительно к общественным проблемам развивали социологи-позитивисты О. Конт, Г. Спенсер, А. Смолл, Л. Уорд, для которых эталоном по-прежнему служило равновесие физических систем. В начале 20 в. концептуальные основания Р. т. несколько видоизменяются под влиянием организмического мышления: эталоном равновесия выступает теперь не механическая система, а живой организм, где это равновесие обеспечивается за счёт сложных процессов внутренней регуляции. Одним из первых такой подход реализовал А. А. , который своей тектологией предвосхитил некоторые положения кибернетики и современного системного подхода, но в то же время допустил ряд серьёзных механистических просчётов и упрощений. В 20-е гг. Р. т. нашла приверженцев в лице ряда сов. философов-механистов (Д. Сарабьянов, И. И. Скворцов-Степанов и др.), которые фактически противопоставляли положения Р. т. учению диалектического материализма о единстве и борьбе противоположностей, рассматривая скачки как «процессы нарушения равновесия». Р. т. послужила методологической основой правоуклонистских идей Н. И. Бухарина, затушёвывавших противоречия в развитии производственных отношений в период построения социализма.

  С конца 30-х гг. некоторые идеи Р. т. получают новое оформление, причём речь уже идёт не о развёрнутой теоретической схеме, а лишь о принципе объяснения. Использование этого принципа было в значительной мере стимулировано развитым в рамках физиологии и кибернетики принципом и изучением в естественных науках и технике устойчивых состояний. Модель динамического равновесия берётся на вооружение многими представителями в буржуазной социологии, у которых идея равновесия приобретает консервативный идеологический подтекст. Многие буржуазные социологи выступают с критикой функционалистской Р. т., отмечая, что она имеет дело лишь с идеальными сбалансированными системами, игнорирует внутрисистемные источники нарушения равновесия и потому плохо приспособлена для анализа процессов социального изменения. Эти слабости особенно явственны в эмпирически ориентированных направлениях социологии - в индустриальной социологии, в работах по «человеческим отношениям» в промышленности, в «управленческой науке», специализирующихся на разработке методов манипуляции людьми для обеспечения равновесия в функционировании буржуазного общества.

  Марксизм-ленинизм принципиально отвергает Р. т. как теоретическую конструкцию, вскрывая консервативно-охранительские предрассудки её представителей. Вместе с тем это не означает отбрасывания понятия равновесия и связанного с ним понятия устойчивости: эти понятия играют важную эвристическую роль в изучении динамически развивающихся систем, выступая в качестве одной из условных точек отсчёта; проблема заключается лишь в том, что на основе этих понятий нельзя построить целостного объяснения процессов в соответствующих системах.

  Лит.:Комаров М. С., Функциональное объяснение в современной буржуазной социологии, в кн.: Актуальные проблемы развития конкретных социальных исследований, М., 1971; Russet С. Е., The concept of equilibrium in American social thought. New Haven - L., 1966.

  Л. А. Седов.

Равновесный процесс

Равнове'сный проце'ссв термодинамике, процесс перехода термодинамической системы из одного равновесного состояния в другое, столь медленный, что все промежуточные состояния можно рассматривать как равновесные. Р. п. характеризуется очень медленным, в пределе бесконечно медленным, изменением термодинамических .Всякий Р. п. является , и, наоборот, любой обратимый процесс является равновесным.

Равнодействующая

Равноде'йствующаясистемы сил, сила, эквивалентная данной системе сил и равная их геометрической сумме: R= е F _k .Система сил, приложенных к одной точке, всегда имеет P., если R¹ 0 .Любая другая система сил, приложенных к телу, если R¹ 0 ,имеет P., когда главный момент этой системы или равен нулю или перпендикулярен R(см. ). В этом случае замена системы сил их Р. допустима лишь тогда, когда тело можно рассматривать как абсолютно твёрдое, и недопустима, например, при определении внутренних усилий или решении др. задач, требующих учёта деформации тела. Примерами систем сил, не имеющих P., являются или две силы, не лежащие в одной плоскости.

Равноденствие

Равноде'нствие,момент времени, в который центр солнечного диска при своём видимом годичном перемещении по эклиптике пересекает небесный экватор. В дни Р. продолжительность дня на всей Земле, исключая районы земных полюсов, почти равна продолжительности ночи, отличаясь от 12 члишь на несколько минут вследствие рефракции и значительной величины углового диаметра Солнца.

  Точка, в которой центр Солнца пересекает экватор при движении из Юж. полушария в Северное, называется точкой весеннего равноденствия, противоположная - точкой осеннего равноденствия. Вследствие того, что промежуток времени между двумя последовательными прохождениями Солнца через одну и ту же точку Р. (тропический год) не совпадает с продолжительностью календарных лет, моменты Р. из года в год перемещаются относительно начала календарных суток. Моменты Р. наступают в простой год на 5 ч 48 мин46 секпозднее, чем в предшествующий, а в високосный - на 18 ч 11 мин14 секраньше; поэтому моменты Р. могут приходиться на две соседние календарные даты. В настоящее время (2-я половина 20 в.) Солнце проходит точку весеннего Р. 20 и 21 марта (этот момент считается началом астрономической весны в Северном полушарии), а точку осеннего Р. 23 сентября (начало астрономической осени в Северном полушарии); приведённые даты указаны в новом стиле при начале суток по московскому времени.

  (2 в. до н. э.) обнаружил, что точки Р. медленно перемещаются вдоль эклиптики навстречу видимому годичному движению Солнца. Это перемещение, объясняемое оси вращения Земли, имеет период около 26 000 лет. В 1737 Дж. открыл явление земной оси, вследствие которой точки Р. совершают колебательные движения с периодом в 18,6 года относительно среднего положения, определяемого их прецессионным перемещением. С изменением положения точек Р. связаны изменения небесных координат светил. В звёздных каталогах приводятся места звёзд для определённого положения точки весеннего Р., эпоха которого указывается.

Равнокрылые
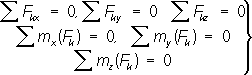