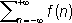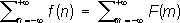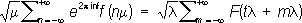 |
|
|
|
()ModernLib.Net / / / () - (. 2)
И. Д. Рожанский. Пуассона интеграл Пуассо'на интегра'л,1) интеграл вида
где rи j - полярные координаты, q - параметр, меняющийся на отрезке [0; 2p]; П. и. выражает значения функции u( r, j), гармонической внутри круга радиуса R,через её значения f(q), заданные на границе этого круга. Функция u( r, j) является решением задачи Дирихле для круга (см. ). П. и. был впервые рассмотрен С. Д. (1823). Строгая теория П. и. была создана Г. (1869). 2) Интеграл
встречается в теории вероятностей и некоторых задачах математической физики. С. Д. Пуассон предложил весьма простой приём для вычисления этого интеграла. Впервые же этот интеграл был вычислен (1729) Л. , поэтому называется также интегралом Эйлера - Пуассона. Пуассона коэффициент
Пуассо'на коэффицие'нт,одна из физических характеристик материала упругого тела, равная отношению абсолютных значений относительной поперечной деформации элемента тела к его относительной продольной деформации. Введён С. Д.
.При растяжении прямоугольного параллелепипеда в направлении оси
х(
рис.
) имеют место вдоль этой оси удлинение
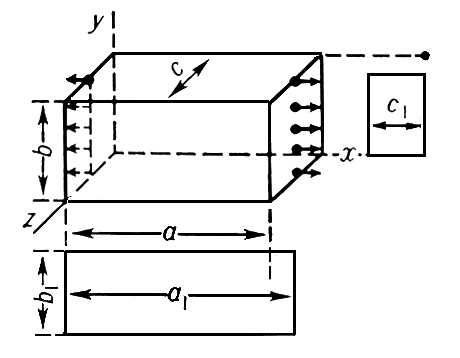
Рис. к ст. Пуассона коэффициент. Пуассона распределение Пуассо'на распределе'ние,одно из важнейших распределений вероятностей случайных величин, принимающих целочисленные значения. Подчинённая П. р. случайная величина Хпринимает лишь неотрицательные значения, причём Х = kcвероятностью
(l - положительный параметр). Своё название «П. р.» получило по имени С. Д. (1837). Математическое ожидание и дисперсия случайной величины, имеющей П. р. с параметром l, равны l. Если независимые случайные величины X 1и X 2имеют П. р. с параметрами l 1и l 2 ,то их сумма X 1+ X 2имеет П. р. с параметрами l 1+ l 2. В теоретико-вероятностных моделях П. р. используется как аппроксимирующее и как точное распределение. Например, если при nнезависимых испытаниях события A 1,..., A nосуществляются с одной и той же малой вероятностью р,то вероятность одновременного осуществления каких-либо kсобытий (из общего числа n) приближённо выражается функцией p k ( np) (математическое содержание этого утверждения при больших значениях nи 1/ рформулируются ). В частности, такая модель хорошо описывает процесс радиоактивного распада и многие др. физические явления. Как точное П. р. появляется в теории случайных процессов. Например, при расчёте нагрузки линий связи обычно предполагают, что количества вызовов, поступивших за непересекающиеся интервалы времени, суть независимые случайные величины, подчиняющиеся П. р. с параметрами, значения которых пропорциональны длинам соответствующих интервалов времени (см. ). В качестве оценки неизвестного параметра l по nнаблюдённым значениям независимых случайных величин X 1,..., X nиспользуется их арифметическое среднее X= ( X 1+ ...+ X n)/ n,поскольку эта оценка лишена систсматической ошибки и её квадратичное отклонение минимально (см. ).
Лит.:Гнеденко Б. В., Курс теории вероятностей, 5 изд., М. - Л., 1969; Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1, М., 1967.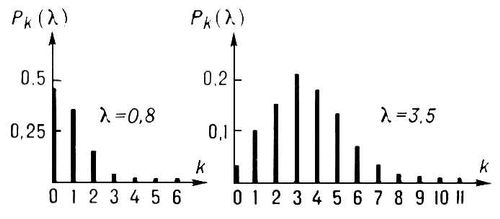 
Рис. к ст. Пуассона распределение. Пуассона теорема Пуассо'на теоре'ма,1) теорема теории вероятностей, описывающая поведение частоты появления некоторого события в последовательности независимых испытаний - частный случай закона больших чисел (точную формулировку см. в ст. ). 2) Одна из предельных теорем теории вероятностей. П. т. позволяет приближённо оценивать вероятность данного числа появлений маловероятного события при большом числе независимых испытаний (см. ). Обе теоремы установлены С. Д. в 1837. Пуассона уравнение Пуассо'на уравне'ние,уравнение с частными производными вида D u= f,где D -оператор Лапласа:
При n= 3 этому уравнению удовлетворяет u( х, у, z) объёмных масс, распределённых с плотностью f( x, у, z)/4p (в областях, где f= 0 потенциал uудовлетворяет уравнению Лапласа), а также потенциал объёмно распределённых электрических зарядов. При этом плотность распределения fдолжна удовлетворять известным требованиям гладкости (например, условию непрерывности частных производных). Если функция fотлична от нуля лишь в конечной области G,ограничена и имеет непрерывные частные производные первого порядка, то при n =2 частное решение П. у. имеет вид:
а при n= 3:
где r( А, Р) - расстояние между переменной точкой интегрирования Аи некоторой точкой Р. В более подробной записи
V(
х, у, z) =
Решение краевых задач для П. у. сводится подстановкой
П. у. впервые (1812) было изучено С. Д. . Пуассона формула суммирования Пуассо'на фо'рмула сумми'рования,формула для вычисления суммы ряда вида
Если
- (несколько иначе, чем обычно, нормированное) функции F( x), то
( mи n -целые). Это и есть П. ф. с.; она может быть записана в более общем виде: если l > 0, m > 0, lm =1 и 0 Ј t <1 ,то
Для справедливости этой формулы достаточно, чтобы в каждом конечном интервале F( x) имела ограниченную вариацию, и для х® + Ґ и х® -Ґ выполнялось одно из условий: 1) F( x) -монотонна и абсолютно интегрируема; 2) F( x) - интегрируема и обладает абсолютно интегрируемой производной. П. ф. с. позволяет в ряде случаев заменить вычисление суммы ряда вычислением суммы др. ряда, сходящегося быстрее первоначального. Пуассоновский поток Пуассо'новский пото'к,то же, что .Этот термин используют, как правило, в . Пуассоновский процесс Пуассо'новский проце'сс,случайный процесс, описывающий моменты наступления 0 < t 1<...< t n<...<... каких-либо случайных событий, в котором число событий, происходящих в течение любого фиксированного интервала времени, имеет и независимы числа событий, происходящих в непересекающиеся промежутки времени. Пусть m( s, t) -число событий, моменты наступления которых t iудовлетворяют неравенствам 0 Ј s < t iЈ t, и пусть l( s, t) -математическое ожидание m( s, t) .Тогда и П. п. при любых 0 Ј s 1 < t 1 Ј s 2 < t 2Ј... Ј s r< t rслучайные величины m( s 1, t 1), m( s 2, t 2),... m( s r, t r) независимы и вероятность того, что m(s, t) = n,равна e - l (s, t)[l( s, t)] n/ n!. В однородном П. п. l( s, t) = a( t - s) ,где а -среднее число событий в единицу времени, расстояния t n -t n-1 между соседними моментами t nнезависимы и имеют с плотностью ae -at, t³ 0. Если имеется много независимых процессов, описывающих моменты возникновения некоторых случайных редких событий, то суммарный процесс при определённых условиях в пределе даёт П. п. П. п. представляет собой удобную математическую модель, которая часто используется в различных приложениях теории вероятностей. В частности, с помощью П. п. описывается поток требований (например, вызовов, поступающих на телефонную станцию, выездов медицинских машин скорой помощи при транспортных происшествиях в большом городе) в . Обобщением П. п. является пуассоновское случайное распределение точек на плоскости или в пространстве, при котором число точек в любой фиксированной области имеет распределение Пуассона (со средним, пропорциональным площади или объёму области) и числа точек в непересекающихся областях независимы. Это распределение часто используется при расчётах в астрономии, физике, экологии, технике и т.д. Лит.:Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., т. 1-2, М., 1967. Б. А. Севастьянов. Пуату Пуату'(Poitou), историческая область на З. Франции, у побережья Атлантического океана. На территории П. - департаменты Вандея, Вьенна, Дё-Севр. П. (без Вандеи) вместе с историческими областями Они, Сентонж и Ангумуа (территория современных департаментов Шаранта и Приморская Шаранта) составляют плановый экономический район Пуату - Шаранта. Площадь П. 20,1 тыс. км 2 .Население 1,1 млн. чел. (1973). Главный город - Пуатье. Территория области - большей частью всхолмлённая равнина; типичен бокаж. Главная отрасль экономики - сельское хозяйство, особенно животноводство (крупный рогатый скот, свиньи) и птицеводство. Основные с.-х. культуры: пшеница, ячмень, кормовые; овощеводство. Промышленность занята главным образом переработкой с.-х. сырья. В гг. Шательро и Пуатье - машиностроение. В районе Мортань - добыча урановой руды (обогащение - на заводе в Экарпьер). Название П. связано с наименованием племени пиктонов, в древности населявших эту территорию. Территория П. входила в .С 9 в. П. - графство. С конца 9 в. графы П. стали герцогами Аквитании; в её составе П. в 1154 стало владением английских королей. В правление Филиппа II Августа (1180-1223) и Людовика VIII (1223-26) территория П. по частям была возвращена Франции и закреплена за ней Парижским договором 1259. В Столетнюю войну 1337-1453 по миру в 1360 П. вновь отошло к Англии, отвоёвано Францией в 1369-73. Во время Великой французской революции П. - один из основных районов, где развернулись .С введением нового административного деления Франции (1790) провинция П. перестала существовать. Пуатье Пуатье'(Poitiers), город на З. Франции, на р. Клен (бассейн Луары), у прохода между Центральным Французским массивом и возвышенностью Гатин. Административный центр департамента Вьенна. 75 тыс. жителей (1968). Машиностроение, пищевая, химическая, кожевенная промышленность. Университет. П. - один из древнейших городов страны, основан галлами. П. в 9-18 вв. - главный город графства и провинции ,в районе которого произошли крупные сражения. В 507 франкский король около П. разбил вестготов, что обеспечило захват франками Южной Галлии. В октябре 732 при П. франкская тяжёлая рыцарская конница под командованием окружила и разгромила арабское войско, вторгшееся из Испании, и остановила продвижение арабов в Европе. Это было первым сражением, исход которого решила рыцарская тяжёлая конница. 19 сентября 1356 около П. (в районе Мопертюи) во время английские войска разбили французские войска короля Иоанна II Доброго, который был взят в плен. Исход сражения был обусловлен превосходством английских лучников над тяжеловооружёнными французскими рыцарями. Поражение явилось одной из причин и . Сохранились фрагменты городских укреплений 12 и 16 вв. Среди памятников архитектуры: баптистерий Сен-Жан [4 в., достройки 7 и 11 вв.; ныне музей (меровингское искусство)]; романские собор Сен-Пьер (1166-1271, достройки 13-15 вв.), церкви Сент-Радгонд (11-14 вв.), Сент-Илер-ле-Гран (11-12 вв.), Нотр-Дам-ла-Гран (11-16 вв.); готическая церковь Сен-Поршер (в основном 16 в.) и фрагменты герцогского замка 12-15 вв., включенного во Дворец юстиции (19 в.). Музей изящных искусств (преимущественно французская школа) в неоренессансной ратуше (1869-76). Лит.:Claude D., Topographie und Verfassung der Stдdte Bourges und Poitiers bis in das 11 Jahrhunderts, Lьbeck - Hamb., 1960; Dez G., Histoire de Poitiers, Poitiers, 1969. 
Пуатье. Баптистерий Сен-Жан. Основное строительство - 4 в. Публиканы Публика'ны(лат. publicani, от publicum - государственное имущество), в Древнем Риме лица (обычно ) ,получавшие с торгов на откуп государственное имущество (земли, рудники, солеварни) с целью его эксплуатации, а также право на сбор государственных налогов и подряды на общественные постройки или снабжение. При крупных сделках создавались компании П., бесконтрольно эксплуатировавшие и разорявшие население, особенно в провинциях. Со времени империи (с 1 в. н. э.) деятельность П. стала ограничиваться, сбор налогов был передан государственным должностным лицам. Публикация Публика'ция(от лат. publico - объявляю всенародно), 1) доведение чего-либо до всеобщего сведения посредством печати, радиовещания или телевидения. 2) Печатание в различных изданиях (газетах, журналах, книгах) отдельных работ. 3) Текст, опубликованный в каком-либо издании. Публицистика Публици'стика(от лат. publicus - общественный), род произведений, посвященных актуальным вопросам и явлениям текущей жизни общества и содержащих фактические данные о различных её сторонах, оценки с точки зрения социального идеала автора, а также представления о путях и способах достижения выдвинутых целей. Содействуя формированию общественного мнения, взглядов, интересов и стремлений людей, влияя на деятельность социальных институтов, П. играет важную политическую и идеологическую роль в жизни общества, служит острым оружием идейной борьбы, средством общественного воспитания, и ,способом организации и передачи социальной информации. П. обращается к явлениям современности во всём богатстве складывающихся в ней конкретных социальных ситуаций (в общественно-политической, экономической, культурно-идеологической и др. сферах). Характеризуя задачи публицистической деятельности большевиков, В. И. Ленин писал: «Мы должны делать постоянное дело публицистов - писать историю современности и стараться писать её так, чтобы наше бытописание приносило посильную помощь непосредственным участникам движения и героям-пролетариям там, на месте действий, - писать так, чтобы способствовать расширению движения, сознательному выбору средств, приемов и методов борьбы, способных при наименьшей затрате сил дать наибольшие и наиболее прочные результаты» (Полн. собр. соч., 5 изд., т. 9, с. 208). По природе своей обязанная «поспевать за событиями» и давать оценку явлениям текущей действительности, опираясь на фундаментальные социально-политические идеи, П., подчёркивал Ленин, обладает способностью «... подводить итоги, делать выводы, почерпать из опыта сегодняшней истории уроки, которые пригодятся завтра, в другом месте...» (там же) и таким образом активно влияет на формирование мировоззрения. Отображение и оценка ситуаций современности в произведениях П. протекает в свете социально-классовых идеологических позиций публициста как представителя определённых социальных сил и сопровождается проповедью (открытой или замаскированной в зависимости от политической ситуации и цензурных условий) идеалов социального устройства и путей их осуществления. Прогрессивная П. всегда стремилась создавать правдивую картину жизни, верно оценивать явления современности, выносить справедливые приговоры и показывать реальные перспективы. П. содержит огромный документальный материал о самых различных явлениях социальной жизни, поэтому для последующих поколений произведения П. выступают как летопись общественно-политич. борьбы, исторический источник, содержащий обширные фактические данные, характеристики позиций различных социальных сил, а также образные зарисовки событий, характеров, быта, сведения по науке, культуре и т.д. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 |
|||||||
,
;
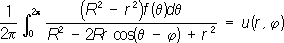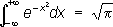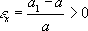, а вдоль перпендикулярных осей
уи
z- сжатие
,
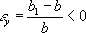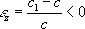, т. е. сужение его поперечного сечения. П. к. равен n
=
½e
y½/e
х
или n
zx
=
½e
z
½/e
х.Для изотропного тела величина П. к. не меняется ни при замене растяжения сжатием, ни при перемене осей деформации, т. е. n
xy
= n
yx=n
zx
= n. В анизотропных телах П. к. зависит от направления осей (т. е.
n
xy
¹ n
yx
¹ n
zx
)
.П. к. вместе с одним из
определяет все упругие свойства изотропного тела. Величина П. к. для большинства металлических материалов близка к 0,3.
,
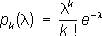k=
0, 1, 2,...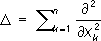
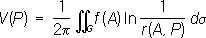
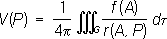
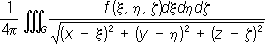
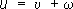к решению краевых задач для уравнения Лапласа Dw = 0.
