 |
|
Популярные авторы:: Борхес Хорхе Луис :: Грин Александр :: Азимов Айзек :: Толстой Лев Николаевич :: Раззаков Федор :: Горький Максим :: Сименон Жорж :: Чехов Антон Павлович :: Картленд Барбара :: Желязны Роджер Популярные книги:: Дюна (Книги 1-3) :: The Boarding House :: Никто не любит Крокодила :: Человек, который принял свою жену за шляпу :: Улики :: Полет :: Бессмертие человеческой личности как научная проблема :: Кот, который гулял под землей :: Опасная любовь :: Созвездие Ворона |
Большая Советская Энциклопедия (ОР)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ОР) - Чтение (стр. 21)
Крупнейшие предприятия: комбинат «Южуралникель», заводы - по обработке цветных металлов, нефтеперерабатывающий (получает нефть из Казахстана, Западной Сибири и Башкирии), синтетического спирта, тяжёлого машиностроения (машины для металлургической и горнорудной промышленности), а также заводы: строительных машин, электромонтажных изделий, металлоконструкций; крупный мясокомбинат; швейная, трикотажная и кондитерская фабрики. Педагогический институт, филиал Всесоюзного заочного политехнического института, техникумы: нефтяной, индустриальный, машиностроительный, вечерний строительный; медицинское и музыкальное училища. Драматический театр, краеведческий музей. Город награжден орденом Трудового Красного Знамени (1971).

Орск. Площадь имени Т. Г. Шевченко. Орско-халиловский металлургический комбинат О'рско-хали'ловский металлурги'ческий комбина'т(ОХМК), крупное предприятие чёрной металлургии СССР с замкнутым металлургическим циклом. Находится в г. Новотроицке (близ г. Орска) Оренбургской области РСФСР. Основан в 1939, построен после Великой Отечественной войны 1941-45 (вступил в строй в 1955). Работает на базе железной руды Халиловского месторождения и коксующегося угля Карагандинского бассейна. Во время Великой Отечественной войны поставлял металлургии Урала марганцевую руду, месторождение которой находилось в 11 кмот строительной площадки ОХМК. В составе комбината (1973) 38 основных, вспомогательных и подсобных цехов, железорудное месторождение, карьеры известняка и огнеупорной глины. Товарная продукция: чугун, сталь, прокат, шамотные огнеупоры, кокс и коксохимические продукты, гранулированный шлак, товары народного потребления. В 1973 производство составило: чугуна 2,2 млн. т, стали 3,3 млн. т, проката 2,7 млн. т. Награжден орденом Трудового Красного Знамени (1971). И. А. Руденко. Орт (в горном деле) Орт(нем. Ort, буквально - место) в горном деле, горизонтальная подземная горная выработка, не имеющая непосредственного выхода на поверхность и проведённая в сторону кровли или почвы пласта полезного ископаемого или от кровли до почвы. Орт (матем.) Орт(от греч. orthуs - прямой) (матем.), то же, что . Орта Виктор Орта',Хорта (Horta) Виктор (6.1.1861, Гент, - 8.9.1947, Брюссель), бельгийский архитектор. Учился в АХ в Генте (с 1876) и Брюсселе (с 1880) у А. Бала. Профессор Свободного университета в Брюсселе (1892-1912), АХ в Антверпене (1919-27) и Брюсселе (1912-31, в 1927-1931 директор). Один из создателей стиля , О. стремился на практике воплотить идею цельного произведения искусства. Для его построек (в основном особняки) характерны свобода планировки, уподобление конструкций природным формам, пластичность объёмно-пространственные композиции (как интерьеров, так и фасадов), широкое применение металла и стекла, выявление их декоративных возможностей и, главное, - органическое единство всех компонентов сооружения (вплоть до деталей внутреннего убранства). В декоре интерьеров, а позже и фасадов О. использовал обильный растительный орнамент, первым ввёл в стилистику «модерна» гибкую, упругую линию («удар бича»). Основные постройки: особняки Тасселя (1892-93) и Сольве (1895-1900), Народный дом, магазин «Инновасьон» (1901) - все в Брюсселе. Позднее О. перешёл на позиции (Центральный вокзал в Брюсселе). Лит.:Delevoy R. L., Victor Horta, Brux., 1958. Т. И. Володина. Ортач Юсуф Зия Орта'ч(Ortaз) Юсуф Зия (1895, Стамбул, - 11.3.1967, там же), турецкий поэт, драматург. Учился в Стамбульском университете. Преподавал литературу в школе (1915-45). В 1946 был избран депутатом меджлиса. Печатался с 1914. Приобрёл известность как один из поэтов-хеджеистов (сторонников силлабического метра), которые сыграли значительная роль в обновлении поэтических форм и литературного языка, приблизив его к народному турецкому языку. Автор сборников лирических стихов «Горизонты битвы» (1917), «Дорога влюблённых» (1919), «Вулкан» (1928) и др. Сатирические стихи публиковал под псевдонимом Щипок (Зimcik). Историческая пьеса «Бинназ» (1919) - первое драматическое произведение в турецкой литературе, написанное силлабическим стихом. О. принадлежат также рассказы, романы, путевые очерки и критические заметки. Соч.: Bir servi gцlgesi, Ist., 1938; Gьn dogmadan, Ist., 1960; Bir rьzgвr esti, Ist., 1962; Bizim yoku_, Ist., 1966. Лит.:Алькаева Л. О., Очерки по истории турецкой литературы, М., 1959; Necatigil В., Edebiyatimizda isimler sцzlьgь, 7 bs., Ist., 1972. Х. А. Чорекчян. Ортега-и-Гасет Хосе Орте'га-и-Гасе'т(Ortega у Gasset) Хосе (9.5.1883, Мадрид, - 18.10.1955, там же), испанский философ-идеалист, публицист и общественный деятель. Сын литератора. Окончил Мадридский университет, затем изучал философию в университетах Лейпцига, Берлина и Марбурга. В 1910-36 возглавлял кафедру метафизики Мадридского университета. Активно выступал как журналист: был основателем и сотрудником журнала «Espaсa» (1915-24), «El Sol» (1916-37) и др.; издававшийся им общественно-политический ежемесячник «Revista de Occidente» (1923-1936) пользовался мировой известностью. Антимонархист; в 1931-33 депутат первых республиканских кортесов; один из основателей «Республиканского объединения интеллигенции» (1931). С началом гражданской войны (1936) эмигрировал в Латинскую Америку; в 1945 вернулся в Европу, в 1948 - в Испанию, где под его руководством был основан институт гуманитарных наук. До конца жизни оставался открытым противником франкизма. Философские взгляды О.-и -Г. складывались под влиянием марбургской школы (Г. ). Неокантианский тезис о самополагании познающего субъекта в процессе развития культуры он стремился раскрыть в дальнейшем как жизненное выражение субъекта в историческом бытии, которое он вначале в духе (особенно Г. и М. ) трактовал антропологически, затем под влиянием немецкого (М. ) - как духовный опыт непосредственного переживания, как «вслушивание» в жизнь с помощью «жизненного разума» (свой синтез различных философских концепций О.-и-Г. называл «рациовитализмом»). В социологии наибольшую известность получило сочинение О.-и-Г. «Восстание масс» (1929-30). Исходя из противопоставления духовной «элиты», творящей культуру, и «массы» людей, довольствующихся бессознательно усвоенными стандартными понятиями и представлениями, он считает основным политическим феноменом 20 в. идейно-культурное разобщение «элиты» и «масс», а следствием этого - общую социальную дезориентацию и возникновение «массового общества». В эстетике выступал как теоретик («Дегуманизация искусства», 1925). Оказал большое влияние на философскую и общественную мысль Испании, особенно в 1910-1920-е гг., а также на европейскую буржуазную социологию (главным образом в постановке проблем и ). Соч.: Obras completas, v. 1-11, Madrid, 1953-70; Obras ineditas, v. 1-7, Madrid, 1957-62; El espectador, v. 1-8, Madrid, 1960-63; в рус. пер. - Дегуманизация искусства, в кн.: Современная книга по эстетике, М., 1957. Лит.:Давыдов Ю. Н., Искусство и элита, М., 1966; Бондаренко Н. Д., Некоторые аспекты проблемы человека в философии Ортега-и-Гассета, в кн.: Историко-философский сборник, М., 1968; Долгов К. М., Философия культуры и эстетика Xoce Ортеги-и-Гассета, в кн.: О современной буржуазной эстетике, в. 3, М., 1972; Ferrater Mora J., Ortega у Gasset: an outline of his philosophy, L., 1956; Abellan J. L., Ortega у Gasset en la filosofнa espanola, Madrid, [1966]; Morуn A. C., El sistema de Ortega у Gasset, Madrid, 1968; Aguado E., Ortega у Gasset, Madrid, 1970. В. С. Муравьев. Ортелий Абрахам Орте'лий(Ortelius, Oertel) Абрахам (4.4.1527 - 28.6.1598), фламандский картограф. В 1570 издал в Антверпене сборник «Театр Мира», включавший 53 карты с подробными географическими текстами; в дальнейшем сборник неоднократно дополнялся и переиздавался (в 1579 О. впервые включил в него 3 исторические карты). Наряду с атласом Г. сборник О. сыграл важную роль в развитии картографии. Ортикон Ортико'н(от греч. orthуs - прямой, правильный и eikMn - изображение), с мозаичным фотокатодом, в которой световое изображение преобразуется в электрическое, считываемое пучком медленных (коэффициент вторичной эмиссии < 1) электронов. О. предложен в 1939 американским инженером А. Розом и Х. Ямсом. Передаваемое изображение проецируется на мишень О. - тонкую стеклянную пластинку, покрытую со стороны объекта полупрозрачным электропроводящим слоем, служащим сигнальной пластиной, а со стороны электронного прожектора - мелкозернистым фотоактивным слоем, являющимся мозаичным фотокатодом. Фототек заряжает элементарные конденсаторы, образованные зёрнами мозаики и сигнальной пластиной, создавая на поверхности мишени т. н. потенциальный рельеф. Периодический разряд конденсаторов осуществляется электронным лучом, построчно обегающим мишень со стороны мозаики. При этом в цепи сигнальной пластины формируется . Характеристика свет - сигнал О. линейна во всём рабочем диапазоне освещённостей. О. примерно в 20 раз чувствительнее , главным образом благодаря более эффективному использованию фототока. В 50-х гг. 20 в. О. вытеснен более совершенным . А. А. Жигарев. Ортис Фернандо О'ртис,Ортис-и-Фернандес (Ortiz-y-Fernandez) Фернандо (16.6.1881, Гавана, - 11.4.1969, там же), кубинский учёный, специалист в области истории, этнографии, социологии, фольклора. Образование получил в Мадридском, Барселонском и Гаванском университетах. В 1915-25 член палаты депутатов. С 1910 редактор журнала «Revista Bimestre cubana», основатель (1924) журнала «Archivos del Folklore cubano» и его редактор до 1929. О. положил начало изучению этнографии на Кубе. В 1926 основал Испано-кубинский институт культуры, в 1937 создал общество афро-кубинских исследований. С 1942 вёл курс этнографии Кубы в Гаванском университете. С 1945 президент Кубино-советского института культуры. С 1959 член Национальной комиссии АН Кубы. Основные труды освещают вклад негров в формирование кубинской нации и создание кубинской культуры. Соч.: Намра afro-cubana. Los negros esclavos, La Habana, 1916: La crisis polнtica Cubana, La Habana, 1919; Contrapunteo cubano del Tabaco у el Azъcar, La Habana, 1940; Historia de una pelea cubana contra los demonios, La Habana, 1960; [Список трудов], «Bohemia», 1969, № 16. Лит.:«Куба», 1969, № 7, 12. Ортит Орти'т(от греч. orthуs - прямой), алланит [от имени английского минералога Т. Аллана (Th. Allan)], минерал из группы эпидота, смоляно-чёрного или жёлто-бурого цвета с ярким блеском. Приближённая формула (Са, Се, Mn) 2(Fe 2+, Fe 3+Mg) Al 2[SiO 4][Si 2O 7] O (OH). Содержание Се 2Оз достигает 6%. Часто содержит примеси Th, U, иногда Y 2O 3(до 8%). Нередко наблюдаются изменённые, гидратированные О., перешедшие в метамиктное состояние (см. ). О. встречается обычно в виде удлинённых плоскопризматических кристаллов моноклинной системы. Образует также неправильные скопления, отдельные зёрна и т.п. Твердость по минералогической шкале 6; хрупок; плотность 4100 кг/ м 3(у измененных разновидностей уменьшается до 2700 кг/ м 3). Радиоактивен. Встречается в природе редко; обычно в пегматитовых жилах совместно с др. минералами, а также в виде отдельных кристаллов, рассеянных в гранитах. О. служит ценным сырьём для извлечения редкоземельных элементов Се, Y и др. Ортлес О'ртлес,Ортлер (Ortles, Ortler), горный массив на Ю. Альп, в Италии и Швейцарии. Высота до 3899 м. Периферийные части сложены преимущественно слюдистыми и кристаллическими сланцами, осевая зона - известняками и доломитами. До высоты 2300 м- лиственные и хвойные леса и субальпийские кустарники, выше - альпийские луга, на вершинах - вечные снега и около 60 ледников. Туризм, альпинизм. Ортогенез Ортогене'з(от греч. orthуs - прямой и ), ортоэволюция, гипотеза, утверждающая, что эволюция живого направлена по пути, прямо ведущему к будущей адаптации. Представления об О. коренятся уже во взглядах Ж. Б. . Немецкие учёные В. Хакке (автор термина «О.», 1893) и Т. Эймер (широко пользовавшийся этим термином) исходили из механоламаркистского положения о том, что эволюция основана на непосредственном влиянии факторов внешней среды, сама же организация особи может меняться лишь в известных направлениях; совместное действие этих факторов определяет окончательное направление эволюции. Впоследствии под О. часто понималась эволюция в определённом направлении как под действием исключительно внутренней движущей силы, так и под непосредственным влиянием внешних условий. Концепцию О. противопоставляют обычно современной теории эволюции, согласно которой направленность эволюции - результат действия . Явление направленности, прямолинейности прослеживается как один из элементов в общем процессе эволюции, но оно объясняется ограничениями, накладываемыми особенностями строения организма, т. е. по существу есть результат отбора в прошлых поколениях. См. также , . Лит.:Симпсон Дж. Г., Темпы и формы эволюции, пер. с англ., М., 1948; Шмальгаузен И. И., Проблемы дарвинизма, 2 изд., Л., 1969; Haacke W., Gestaltung und Vererbung, Lpz., 1893; Eimer G. Н. Т., Die Entstehung der Arten, Tl 2 - Die Orthogenesis der Schmetterlinge, Lpz., 1897. А. В. Яблоков. Ортогеосинклиналь Ортогеосинклина'ль,близ- или межконтинентальная , способная к альпинотипной складчатости и сопровождаемая часто начальным магматизмом. Обладает значительным продольным протяжением и является материнской по отношению к складчатому горному сооружению. О. состоит обычно из продольных (эвгеосинклинальных с интенсивным магматизмом и миогеосинклинальных со слабым проявлением или отсутствием магматизма) зон. Термин «О.» предложен в 1940 немецким геологом Х. Штилле. Ортогнатизм Ортогнати'зм(от греч. orthуs - прямой и gnбthos - челюсть), отсутствие или незначительность выступания вперёд верхней челюсти по отношению к общей фронтальной плоскости лица, в отличие от . Степень выступания челюстей находится в слабой взаимозависимости с длиной и шириной лица. Лицевой угол при О. от 85° до 92,9°. Тем же термином и в пределах тех же углов принято обозначать относительную прямоту носового, или среднелицевого, отдела и альвеолярной (см. , 3) части верхней челюсти. О. является исключительной морфологической особенностью человека, связанной с преобладанием у него мозговой части черепа над лицевой. Ортогнатия Ортогна'тия(от греч. orthуs - прямой, правильный и gnбthos - челюсть), один из видов нормального , при котором верхние передние зубы перекрывают нижние примерно на 1/ 3высоты их коронок. Ортогнейс Ортогне'йс(от греч. orthуs - прямой и ), горная порода, образовавшаяся в результате изменения (метаморфизма) изверженных пород (гранитов, кварцевых диоритов и др.), в отличие от , возникшего за счёт осадочных горных пород. Ортогональная матрица Ортогона'льная ма'трицапорядка n
произведение которой на транспонированную матрицу А'даёт единичную матрицу, то есть АА'= Е(а следовательно, и A'A= Е). Элементы О. м. удовлетворяют соотношениям:
или эквивалентным соотношениям:
Определитель | A| О. м. равен +1 или -1. При перемножении двух О. м. снова получается О. м. Все О. м. порядка nотносительно операции умножения образуют , называемую ортогональной. При переходе от одной прямоугольной системы координат к другой коэффициенты a ijв формулах преобразования координат
образуют О. м. См. также . Ортогональная проекция Ортогона'льная прое'кция,частный случай параллельной , когда ось или плоскость проекций перпендикулярна (ортогональна) направлению проектирования. Ортогональная система функций Ортогона'льная систе'ма фу'нкций,система функций {(j n ( x)}, n= 1, 2,..., ортогональных с весом r ( х) на отрезке [ а, b], т. е. таких, что
Примеры. Тригонометрическая система 1,
cos
nx, sin
nx;
n= 1, 2,..., - О. с. ф. с весом 1 на отрезке [-p, p].
Если каждая функция j (
х) из О. с. ф. такова, что
Систематическое изучение О. с. ф. было начато в связи с методом Фурье решения краевых задач уравнений математической физики. Этот метод приводит, например, к разысканию решений для уравнения [r( х) у'] '+ q( x) y= l у, удовлетворяющих граничным условиям у( а) + hy'( a) = 0, y( b) + Hy'( b) = 0, где hи Н- постоянные. Эти решения - т. н. собственные функции задачи - образуют О. с. ф. с весом r ( х) на отрезке [ a, b]. Чрезвычайно важный класс О. с. ф. -
- был открыт П. Л.
в его исследованиях по интерполированию способом наименьших квадратов и проблеме моментов. В 20 в. исследования по О. с. ф. проводятся в основном на базе теории интеграла и меры Лебега. Это способствовало выделению этих исследований в самостоятельный раздел математики. Одна из основных задач теории О. с. ф.- задача о разложении функции
f(
x) в ряд вида
Коэффициенты
С
п, называемые коэффициентами Фурье функции относительно системы {j
n
(
x)}, обладают следующим экстремальным свойством: линейная форма
имеет наименьшее значение по сравнению с ошибками, даваемыми при том же
nдругими линейными выражениями вида
Ряд
3) Не существует отличной от нуля функции с интегрируемым на отрезке [ a, b] квадратом, ортогональной ко всем функциям j n ( x), n= 1, 2,.... Если рассматривать функции с интегрируемым квадратом как элементы , то нормированные О. с. ф. будут системами координатных ортов этого пространства, а разложение в ряд по нормированным О. с. ф. - разложением вектора по ортам. При этом подходе многие понятия теории нормированных О. с. ф. приобретают наглядный геометрический смысл. Например, формула (*) означает, что проекция вектора на орт равна скалярному произведению вектора и орта; равенство Ляпунова - Стеклова может быть истолковано как теорема Пифагора для бесконечномерного пространства: квадрат длины вектора равен сумме квадратов его проекций на оси координат; замкнутость О. с. ф. означает, что наименьшее замкнутое подпространство, содержащее все векторы этой системы, совпадает со всем пространством и т.д. Лит.:Толстов Г. П., Ряды Фурье, 2 изд., М., 1960; Натансон И. П., Конструктивная теория функций, М. - Л., 1949; его же, Теория функций вещественной переменной, 2 изд., М., 1957; Джексон Д., Ряды Фурье и ортогональные полиномы, пер. с англ., М., 1948; Качмаж С., Штейнгауз Г., Теория ортогональных рядов, пер. с нем., М., 1958. Ортогональное преобразование Ортогона'льное преобразова'ние, евклидова векторного пространства, сохраняющее неизменным длины или (что эквивалентно этому) скалярное произведение векторов. В ортогональном и нормированном базисе О. п. соответствует . О. п. образуют - т.н. группу вращений данного евклидова пространства вокруг начала координат. В трёхмерном пространстве О. п. сводится к повороту на некоторый угол вокруг некоторой оси, проходящей через начало координат О, если определитель соответствующей ортогональной матрицы равен +1. Если же этот определитель равен -1, то поворот дополняется зеркальным отражением относительно плоскости, проходящей через Ои перпендикулярной оси поворота. В двумерном пространстве, т. е. в плоскости, О. п. определяет поворот на некоторый угол вокруг начала координат Оили зеркальное отражение относительно некоторой прямой, проходящей через О. Используется О. п. при приведении к главным осям . См. также , . Ортогональность Ортогона'льность(греч. orthogMnios - прямоугольный, от orthуs - прямой и gMnнa - угол), обобщение (часто синоним) понятия . Если два вектора в трёхмерном пространстве перпендикулярны, то их равно нулю. Это позволяет обобщить понятие перпендикулярности, распространив его на векторы в любом линейном пространстве, в котором определено скалярное произведение, обладающее обычными свойствами (см. ), назвав два вектора ортогональными, если их скалярное произведение равно нулю. В частности, вводя скалярное произведение в пространстве комплекснозначных функций, заданных на отрезке [ а, b] формулой
где r( х) ³ 0, называют две функции f( x) и j( x), для которых ( f, j) r= 0, то есть
ортогональными с весом r( х). Два линейных подпространства называется ортогональными, если каждый вектор одного из них ортогонален каждому вектору другого. Это понятие обобщает понятие перпендикулярности двух прямых или прямой и плоскости в трёхмерном пространстве (но не понятие перпендикулярности двух плоскостей). Термином ортогональные кривые обозначают кривые линии, пересекающиеся под прямым углом (измеряется угол между касательными в точке пересечения). См., например, ортогональные траектории в ст. . Ортогональные многочлены
Ортогона'льные многочле'ны,специальные системы многочленов {
р
п(
х)};
n= 0, 1, 2,..., ортогональных с весом r(
х) на отрезке [
а,
b] (см.
). Нормированная система О. м. обозначается через
Многочлен р п( х) такой системы удовлетворяет дифференциальному уравнению
где g n = n[(a 1+ ( n+ 1)b 2]. Наиболее важные системы О. м. (классические) относятся к этому типу; они получаются (с точностью до постоянного множителя) при указанных ниже а, bи r( х). 1)
{
Р
п
(
l,
m)(
х)} - при
а= -1,
b= 1 r(
х) = (1-
х)
l(1 +
x)
m, l > -1, m > -1. Специальные частные случаи многочленов Якоби соответствуют следующим значениям l и m: l = m-
2)
L
n(
x) - при
а= 0,
b= + Ґ и r(
х) =
е
-х(их наз. также многочленами Чебышева - Лагерра) и обобщённые многочлены Лагерра
3)
Н
n(
х) - при
а= -Ґ,
b= + Ґ и
О. м. обладают многими общими свойствами. Нули многочленов р n( х) являются действительными и простыми и расположены внутри [ а, b]. Между двумя последовательными нулями многочлена р n( х) лежит один нуль многочлена p n+1( х). Многочлен р n( х) может быть представлен в виде т. н. формулы Родрига
где
A
n- постоянное, а b(
х) см. формулу (*). Каждая система О. м. обладает свойствами замкнутости. Три последовательных О. м.
где а п+2и l n+2следующим образом выражаются через коэффициенты этих многочленов: если 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25 |
|||||||
 ,
,

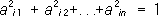
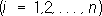
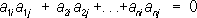


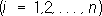


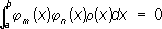
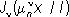 , где
n= 1, 2,...,
, где
n= 1, 2,...,
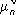 - положительные нули
J
n(
x), образуют для каждого n > -
1/
2О. с. ф. с весом
хна отрезке [0,
l].
- положительные нули
J
n(
x), образуют для каждого n > -
1/
2О. с. ф. с весом
хна отрезке [0,
l].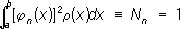 (условие нормированности), то такая система функций называется нормированной. Любую О. с. ф. можно нормировать, умножив j (
х) на число
(условие нормированности), то такая система функций называется нормированной. Любую О. с. ф. можно нормировать, умножив j (
х) на число
 - нормирующий множитель.
- нормирующий множитель. , где {j
п
(
х)} - О. с. ф. Если положить формально
, где {j
п
(
х)} - О. с. ф. Если положить формально
 , где {j
п
(
х)} - нормированная О. с. ф., и допустить возможность почленного интегрирования, то, умножая этот ряд на j
п
(
х) r(
х) и интегрируя от
адо
b, получим:
, где {j
п
(
х)} - нормированная О. с. ф., и допустить возможность почленного интегрирования, то, умножая этот ряд на j
п
(
х) r(
х) и интегрируя от
адо
b, получим: (*)
(*) наилучшим образом приближает в среднем эту функцию. Иными словами, средняя квадратичная ошибка с весом r(
х):
наилучшим образом приближает в среднем эту функцию. Иными словами, средняя квадратичная ошибка с весом r(
х): (*)
(*) . Отсюда, в частности, получается т. н. неравенство Бесселя
. Отсюда, в частности, получается т. н. неравенство Бесселя
 с коэффициентами
С
п, вычисленными по формуле (*), называется рядом Фурье функции
f(
x) по нормированной О. с. ф. {j
n
(
x)}. Для приложений первостепенную важность имеет вопрос, определяется ли однозначно функция
f(
x) своими коэффициентами Фурье. О. с. ф., для которых это имеет место, называется полными, или замкнутыми. Условия замкнутости О. с. ф. могут быть даны в нескольких эквивалентных формах. 1) Любая непрерывная функция
f(
x) может быть с любой степенью точности приближена в среднем линейными комбинациями функций j
k
(
x), то есть
с коэффициентами
С
п, вычисленными по формуле (*), называется рядом Фурье функции
f(
x) по нормированной О. с. ф. {j
n
(
x)}. Для приложений первостепенную важность имеет вопрос, определяется ли однозначно функция
f(
x) своими коэффициентами Фурье. О. с. ф., для которых это имеет место, называется полными, или замкнутыми. Условия замкнутости О. с. ф. могут быть даны в нескольких эквивалентных формах. 1) Любая непрерывная функция
f(
x) может быть с любой степенью точности приближена в среднем линейными комбинациями функций j
k
(
x), то есть
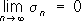 в этом случае говорят, что ряд
в этом случае говорят, что ряд
 сходится в среднем к функции
f(
x)]. 2) Для всякой функции
f(
x), квадрат которой интегрируем относительно веса r(
х), выполняется условие замкнутости Ляпунова - Стеклова:
сходится в среднем к функции
f(
x)]. 2) Для всякой функции
f(
x), квадрат которой интегрируем относительно веса r(
х), выполняется условие замкнутости Ляпунова - Стеклова:
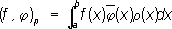 ,
,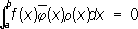 ,
,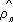 , а система О. м., старшие коэффициенты которых равны 1,- через
, а система О. м., старшие коэффициенты которых равны 1,- через
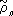 . В краевых задачах математической физики часто встречаются системы О. м., для которых вес r(
х) удовлетворяет дифференциальному уравнению (Пирсона)
. В краевых задачах математической физики часто встречаются системы О. м., для которых вес r(
х) удовлетворяет дифференциальному уравнению (Пирсона)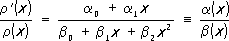

 (их иногда называют многочленами Гегенбауэра); l = m = -
1/
2, т. е.
(их иногда называют многочленами Гегенбауэра); l = m = -
1/
2, т. е.
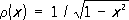 -
1-го рода
T
n(
x); l = m =
1/
2, т. е.
-
1-го рода
T
n(
x); l = m =
1/
2, т. е.
 -
2-го рода
U
n(
x); l = m = 0, т. е. r(
х)
є1 -
Р
п(
х).
-
2-го рода
U
n(
x); l = m = 0, т. е. r(
х)
є1 -
Р
п(
х). - при
- при
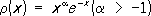 .
. (их называют также многочленами Чебышева - Эрмита).
(их называют также многочленами Чебышева - Эрмита).
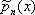 ,
,
 ,
,
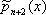 связаны рекуррентным соотношением:
связаны рекуррентным соотношением: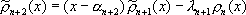 ,
,