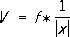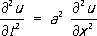|
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Лет за триста до братьев Люмьер :: Вторая книга Царств :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Роковые кости :: Звезды в их руках |
Большая Советская Энциклопедия (ОБ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ОБ) - Чтение (стр. 9)

1. Генерал. 1802. 2. Обер-офицер гренадерского полка. 1812. 3. Рядовой гренадерского полка. 1812. 4. Рядовой егерского полка. 1809. 5. Обер-офицер Кинбурнского драгунского полка. 1812. 6. Рядовой Сумского гусарского полка. 1812. 7. Рядовой Ямбургского уланского полка. 1812. 8. Канонир пешей артиллерии. 1803. 9. Офицер Донского казачьего войска. 1812. 10. Казак Донского Атаманского полка 1814. 11. Матрос. 1802. 12. Штаб-офицер флота. 1803. 
1. Красногвардеец. 1917. 2. Красноармеец. 1918. 3. Краснофлотец. 1918. 4. Командир (кавалерист). 1918. 5. Комиссар. 1918. 6. Красноармеец, летняя форма (пехота). 1919. 7.Командир дивизиона, зимняя форма (артиллерия). 1919. 8. Командир корпуса, летняя форма (кавалерия). 1922. 9. Командир роты, зимняя форма (пехота). 1922. 10. Командир отделения, зимняя форма без шинели (артиллерия). 1923. 11. Красноармеец, зимняя форма (кавалерия). 1924. 12. Лётчик. 1924. 
1. Генерал от инфантерия. 1882. 2. Рядовой 3-го пехотного Нарвского полка. 1882. 3. Унтер-офицер 10-го драгунского Екатерининского полка. 1882. 4. Обер-офицер лейб-гвардии 1-й артиллерийской бригады. 1911. 5. Рядовой 11-го гренадерского Фанагорийского полка. 1911. 6. Обер-офицер лейб-гвардии Гусарского полка. 1911. 7. Рядовой 10-го уланского Одесского полка. 1911. 8. Рядовой 13-го драгунского Военного ордена полка. 1911. 9. Обер-офицер Забайкальского казачьего войска. 1911. 10. Штаб-офицер Кубанского казачьего войска. 1911. 11. Штаб-офицер Генерального штаба. 1912. 12. Обер-офицер 9-го драгунского Казанского полка (форма военного времени). 13. Рядовой пехотного полка (форма военного времени). 
1. Помощник командира 27-го кавалерийского полка, летняя форма. 1927. 2. Майор (пехота). 1935. 3. Лейтенант (ВВС). 1935. 4. Полковник (автобронетанковые войска), парадная вне строя. 1935. 5. Капитан (кавалерия), повседневная. 1935. 6. Кубанский казак, старший лейтенант, парадная форма. 1936. 7. Донской казак, красноармеец, парадная форма. 1936. 8.Красноармеец (пехота), летняя форма. 1936. 9. Красноармеец (артиллерия), зимняя форма. 1940. 10. Маршал Советского Союза, зимняя повседневная форма. 1940. 11. Генерал-майор бронетанковых войск, повседневная форма. 1940. 
Форма одежды маршалов и генералов Советской Армии с 1970: 1. Летняя парадная для строя. 2. Летняя парадная вне строя. 3. Летняя парадная для строя (в авиации). 4. Летняя парадно-выходная. 5. Летняя полевая. Форма одежды адмиралов и генералов ВМФ с 1970: 6. Парадная № 1. 7. Парадная № 3. 8. Повседневная для строя № 4. Форма одежды офицеров и прапорщиков Советской Армии с 1970: 9. Летняя парадная для строя. 10. Зимняя парадная для строя. 11. Летняя повседневная для строя. 12. Летняя полевая. 
1.Генерал-майор артиллерии, повседневная форма. 1943. 2. Лейтенант (пехота), парадная форма. 1943. 3. Лейтенант (артиллерия), зимняя повседневная форма. 1943. 4. Рядовой (пехота), летняя полевая форма. 1943. 5. Капитан 2-го ранга, повседневная форма. 1943. 6. Рядовой морской пехоты. 1944. 7. Маршал Советского Союза, парадная форма вне строя. 1945. 8. Майор авиации, парадно-выходная форма. 1949. 9. Капитан (артиллерия), парадная форма для строя. 1955. 10. Рядовой (пехота), парадная форма. 1956. 11. Лейтенант (артиллерия), повседневная форма. 1958. 
Форма одежды офицеров и мичманов МВФ с 1970: 1. Летняя парадная № 2. 2. Зимняя парадная № 4. 3. Летняя повседневная № 3. 4. Зимняя повседневная № 5. 5. Летняя полевая морской пехоты. 6. Летняя повседневная № 3 вне строя (мичман). Форма одежды старшин, сержантов, матросов и курсантов МВФ с 1970: 7. Зимняя полевая морской пехоты. 8. Летняя № 1. 9. Летняя № 2. 10. Летняя № 3 (нахимовец). 11. Летняя парадная № 3 (курсант). 12. Зимняя № 4. 13. Зимняя № 5. 
1. Мушкетёр пехотного полка. 1763. 2. Обер-офицер пехотного полка. 1763. 3. Обер-офицер Острогожского гусарского полка. 1776. 4. Егерь. 1765. 5. Драгун. 1764. 6. Рядовой мушкетёрского полка. 1786. 7. Матрос. 1764. 8. Штаб-офицер флота. 1764. 9. Гренадёр лейб-гвардии Смёновского полка. 1800. 10. Обер-офицер Изюмского гусарского полка. 1797. 11.Мушкетёр Белозёрского пехотного полка. 1797. 
1. Пеший воин 10-11 вв. 2. Воин 13-14 вв. 3. Стрелец начала 17 в. 4. Стрелец полка Бухвостова. 1674. 5. Стрелец полка Калобова. 1674. 6. Фузилёр лейб-гвардии Преображенского полка. 1700. 7. Обер-офицер лейб-гвардии Преображенского полка. 1700. 8. Фузилёр драгунского полка. 1720. 9. Гренадер пехотного полка. 1700. 10. Бомбардир. 1712. 11. Матрос. 1711. 
1. Обер-офицер лейб-гвардии Московского полка. 1827. 2. Рядовой пехотного полка. 1828. 3. Унтер-офицер гренадерского полка. 1851. 4. Обер-офицер лейб-гвардии Конного полка. 1841. 5. Рядовой Псковского кирасирского полка. 1838. 6. Генерал лейб-гвардии Кирасирского его величества полка. 1844. 7. Генерал Генерального штаба. 1844. 8. Обер-офицер Черноморского казачьего войска. 1842. 9. Рядовой пехотного полка Кавказского корпуса. 1848. 10. Штаб-офицер флота. 1826. 11. Матрос. 1858. 
1. Унтер-офицер лейб-гвардии Измайловского полка. 1870. 2. Рядовой Туркестанского линейного батальона. 1869. 3. Штаб-офицер лейб-гвардии Преображенского полка. 1868. 4. Рядовой лейб-гвардии Кавалергардского полка. 1870. 5. Обер-офицер 12-го гусарского Ахтырского полка. 1878. 6. Рядовой 2-го уланского Курляндского полка. 1868. 7. Обер-офицер Донского казачьего войска. 1867. 8. Рядовой лейб-гвардии Конногренадерского полка (походная форма). 1868. 9. Унтер-офицер 2-го драгунского Псковского полка. 1872. 10. Генерал армейской лёгкой кавалерии. 1868. 11. Унтер-офицер флота. 1881. 12. Штаб-офицер флота. 1892. 
Форма одежды офицеров и прапорщиков Советской Армии с 1970: 1. Летняя парадно-выходная (прапорщик). 2. Летняя парадная для женщин. 3. Летняя полевая для женщин. Форма одежды сержантов, солдат и курсантов Советской Армии с 1970: 4. Летняя парадная. 5. Зимняя парадная. 6. Летняя парадно-выходная (курсант). 7. Летняя повседневная. 8. Летняя повседневная для жарких районов. 9. Летняя повседневная воздушнодесантных войск. 10. Летняя на особый период. 11. Зимняя на особый период. 12. Летняя повседневная № 1 суворовцев. 13. Летняя парадная суворовцев. Обмуровка котла Обмуро'вка котла', система ограждений котлоагрегата , отделяющих его топку и газоходы от окружающей среды. О. к. применяется в котлах, не имеющих цельносварных газоплотных экранов. Назначение О. к. - придать надлежащее направление потоку дымовых газов в котлоагрегате, уменьшить потери тепла в окружающую среду и предотвратить присосы наружного воздуха в газоходы котла при разрежении в них или же выбивание дымовых газов в помещение котельной, если давление в газоходах выше атмосферного. Температура О. к. снаружи не должна превышать 55 °С при температуре воздуха в котельной 25 °С. О. к. выполняют из шамотного кирпича, огнеупорного бетона и др. огнеупоров . Обнажение горных пород Обнаже'ние го'рных поро'двыход коренных горных пород на земную поверхность. О. г. п. чаще всего встречаются по берегам рек, склонам оврагов, на гребнях хребтов и т.п. Кроме естественных, образуемых деятельностью природных агентов (текучие воды, ледники, ветер и т.п.) различают искусственное О. г. п., специально создаваемые или возникающие при разного рода горных выработках (выемки, канавы, колодцы, шурфы, шахты, штольни и др.). Изучение О. г. п. позволяет выяснять геологическое строение местности и широко используется при геологической съёмке. Обнинск О'бнинскгород областного подчинения в Калужской области РСФСР. Расположен на р. Протва (приток Оки). Ж. д. станция на линии Москва-Брянск, в 106 кмк Ю.-З. от Москвы, 61 тыс. жителей в 1974 (в 1959 было 16 тыс. жителей). В О. - первая в мире атомная электростанция (дала ток в 1954). Важный научный центр. Научно-исследовательские институты: медицинской радиологии, физико-энергетический, гидрометеорологической информации; институт экспериментальной метеорологии, сейсмологическая обсерватория и др. научные учреждения. Медицинское училище, музей. Обновленцы Обновле'нцы, сторонники религиозного обновленческого течения внутри русской православной церкви 20-40-х гг. 20 в. Обновленческое течение, нередко именуемое церковным расколом, берёт начало в религиозном реформаторстве конца 19 - начала 20 вв. О. ставили задачей приспособить церковь к изменившимся после Октябрьской революции1917 условиям. Основные группы О.: «Живая церковь» , «Церковное возрождение», «Союз общин древнеапостольской церкви» - возникли в 1922. О. выступили против контрреволюционной деятельности церковного руководства во главе с патриархом Тихоном, провозгласили своим принципом лояльность по отношению к Советскому государству. Идеологи О. (митрополит А. И. Введенский и др.) проповедовали «коммунистическое христианство». Они ратовали за возвращение к т. н. демократическим порядкам раннего христианства, стремились отождествить коммунизм и христианство. О. внесли ряд изменений в церковное устройство, культ и быт духовенства (высшее церковное управление, демократизация прихода, женатый епископ, второбрачие духовенства, богослужение на русских языках и др.). Сущность политической и социальной переориентации О. сводилась к разрыву со старыми, дворянско-бюрократическими традициями. Программа О. разрабатывалась на их Поместных соборах в 1923 и 1925. Деятельность О. в известной степени способствовала эволюции русской православной церкви на пути лояльности к Советской власти. О. как течение прекратило существование вскоре после Великой Отечественной войны 1941-45, когда обновленческое духовенство со своими приходами возвратилось в русскую православную церковь. Лит.:Гордиенко Н. С., Современное православие, М., 1968; Шишкина. а., Сущность и критическая оценка «обновленческого раскола Русской православной церкви, Казань, 1970; Курочкин П. К., Эволюция современного русского православия, М., 1971; Трифонов И. Я., Раскол в русской православной церкви, «Вопросы истории», 1972, №5. Н. П. Красников. Обнорский Виктор Павлович Обно'рскийВиктор Павлович [11(23).11.1851 Грязовец, ныне Вологодской области, - 17.4.1919, Томск], русский рабочий, революционер. Из мещан. В 1869-73 в Петербурге работал слесарем на заводах - патронном, Нобеля, Плисса и др. В конце 1871 - начале 1872 участвовал в создании рабочих кружков. В 1872 был связан с чайковцами . С 1873 на нелегальном положении; выехал в Москву, затем в Одессу. Трижды (начало - конец 1874, ноябрь 1876 - конец 1877, осень - конец 1878) был за границей. Жил в Лондоне, Париже, Женеве. В 1877 один из учредителей в Женеве «Общества пособия политическим изгнанникам из России». Работал слесарем на швейцарских заводах. Ознакомился с документами и деятельностью 1-го Интернационала и западно-европейского рабочего движения. Поддерживал связь с представителями различных течений русской революционной эмиграции. В начале 1875 под фамилией Павлов вёл пропаганду среди крестьян Архангельской губернии. В июле 1875-1-й половине 1876, январе - августе 1878 участвовал в организации «Северного союза русских рабочих» в Петербурге и Москве, был одним из авторов его программы. В конце 1878 посетил Краков и Варшаву, положив начало связи польских социалистов с «Северным союзом русских рабочих». Арестован в Петербурге 29 января 1879. В июне 1880 осуждён на 10 лет каторг, которую отбывал на Каре. С июня 1884 на поселении в Забайкальской области, работал слесарем на приисках. С 1909 жил в г. Кузнецке (ныне г. Новокузнецк) под надзором полиции. После Февральской революции 1917 избран в городской Комитет общественных организаций. Приветствовал победу Октябрьской революции 1917. Лит.:Мирошников И., В. Обнорский - выдающийся рабочий-революционер, М., 1960; Егоров В. А., Виктор Павлович Обнорский, Архангельск, 1967. Е. К. Жигунов. 
В. П. Обнорский. Обнорский Сергей Петрович Обно'рскийСергей Петрович [14(26).6.1888, Петербург, - 13.11.1962, Москва], советский языковед, академик АН СССР (1939; член-корреспондент 1931). Окончил Петербургский университет (1910). Профессор Пермского (1916-22) и Ленинградского (с 1922) университетов. Главные исследования посвящены истории русского языка, диалектологии и лексикографии. Выдвинул оригинальную теорию русской народной основы древне-русской литературы языка (в отличие от теории о церковно-славянских истоках русского литературного языка). Основные труды по морфологии имени и глагола русского языка, а также работ по культуре русской речи, особенно в области орфографии, произношения и грамматических форм. О. - редактор академического словаря русского языка (1912-37), член редколлегии 17-томного академического словаря современного русского литературного языка (1950-65). Основатель и первый директор (1944-50) института русского языка АН СССР. Государственная премия СССР (1947), Ленинская премия (1970, посмертно). Член-корреспондент Болгарской и Чешской АН, доктор honoris causa университета в Осло. Награжден 3 орденами Ленина, а также медалями. Соч.: Именное склонение в современном русском языке, в. 1-2, Л., 1927-30; Очерки по истории русского литературного языка старшего переда, М. - Л, 1946; Очерки по морфологии русского глагола, М., 1953. Лит.:Виноградов В. В., Научная деятельность академика С. П. Обнорского, «Известия АН СССР. ОЛЯ», 1958, т. 17, в. 3; Филин Ф. П., Сергей Петрович Обнорский, «Русский язык за рубежом, 1972, №2. Ф. П. Филин. 
С. П. Обнорский. Обнос Обно'с, ограждение устройств, выступающих за габариты корпуса речного судна. Площадки О., поддерживаемые кронштейнами, служат продолжением палубы . Обобщение Обобще'ние, форма приращения знания путём мысленного перехода от частного к общему, которой обычно соответствует и переход на более высокую ступень абстракции . Пример: переход от наблюдения над совокупностями индивидуализированных объектов к мысленному их разбиению на классы равночисленных совокупностей и далее к понятию натурального числа. О. - одно из важнейших средств научного познания, позволяющее извлекать общие принципы (законы) из хаоса затемняющих их явлений, унифицировать и в «единой формуле» отождествлять множества различных вещей и событий. По семантико-гносеологическому содержанию О. делятся на два основных типа: 1) порождающие новые семантические единицы (концепты), т. е. такие понятия, законы, принципы и теории, которые не детерминируются исходным семантическим полем (первичной семантикой), и 2) не порождающие таковых. Последние могут давать лишь новые варианты старых значений; они имеют более простую структуру сравнительно с первыми и часто являются их предельными случаями. Ко 2-му типу, в частности, принадлежат: экстраполяция (например, распространение квантовой интерпретации закона теплового излучения Планка на область световых явлений, позволившее объяснить фотоэффект ), неполная индукция (например, распространение на все вещества известного из опыта свойства ряда веществ находиться в трёх агрегатных состояниях) и "-обобщение чистой логики предикатов , являющееся по существу синонимич. переходом от А( х) к "xA( x) ,где условие А( х) мыслится в интерпретации всеобщности. К 1-му типу относятся все т. н. теоретические О., или О. через абстракцию, которым в познании соответствует переход от абстракции n-го порядка к абстракциям более высокого порядка, В частности, это естественное для логики О. посредством замены постоянных переменными, позволяющее выделять «в чистом виде» такие сущности, как «свойство» и «отношение»; это - О. на основе идеализированного эксперимента, наводящего на умозрительные принципы, подобные принципу инерции или принципу относительности, а также О. через отождествление по свойству, позволяющее выявить общую сущность по-разному воспринимаемых явлений например то что магнетизм, электричество и свет суть лишь разные проявления электромагнитного поля. К 1-му типу относится и "-обобщение прикладной логики («правило Локка», широко применяемое в практике математических доказательств , когда при переходе от частного значения хко всем хв интервале абстракции отождествления обеспечивается сохранение истинности предиката, установленного для частного значения. Это всегда возможно, если истинность предиката зависит не от частного значения х,а только от определяемой соответствующим отождествлением области его изменения - от класса абстракции, обобщённым представителем которого (эталоном) служит в этом случае данное частное значение (см. Абстракции принцип ). При этом, в отличие от "-обобщения чистой логики, возникает и новый семантический контекст О.: первоначальная условная интерпретация посылки заменяется интерпретацией всеобщности, а относимое к содержанию частного значения понятие класса абстракции входит в содержание подкванторной переменной, делая квантор ограниченным. Но в тех случаях, когда класс абстракции совпадает с универсальным классом, "-обобщенис прикладной логики переходит в "-обобщение чистой логики. Исторически процесс развития понятий и теорий выражается в приращении знания посредством цепей обобщений, звеньями которых служат О. 1-го или 2-го типов. В цепях О. отражаются последовательные связи сущностей 1-го с сущностями 2-го, 3-го и так далее порядков. Эти связи различны, и в зависимости от их характера им соответствуют или цепи О. с сохраняющейся семантикой исходных концептов или, напротив, изменяющие первичную семантику. Примером может служить последовательное О. понятия числа путём построения систем натуральных, целых, рациональных, действительных и комплексных чисел. Для этой цепи, сохраняющей первичную семантику, характерны такие расширения исходной области, которые удовлетворяют принципу постоянства формальных законов, согласно которому законы операций, определяемых для элементов исходной области, при всех последующих её расширениях должны сохраняться и для новых элементов. Эта цепь, однако, не может быть сколь угодно продолжаемой. Уже арифметика трансфинитных количественных чисел не удовлетворяет вышеназванному принципу, но возникающий при этом переход к общему понятию количественного числа приводит и к новому пониманию арифметики натуральных чисел как арифметики мощностей конечных множеств. Примером цепи О. 2-го вида может служить переход от классической логики к интуиционистской (см. Логика ), а также последовательный переход от классической механики к релятивистской механике и общей теории относительности. В подобных переходах более общая теория может иметь законченную формулировку независимо от менее общей, но она должна содержать в себе последнюю в качестве предельного случая, что составляет основное содержание принципа соответствия для цепей О. с изменяющейся первичной семантикой. Лит.:Пойа Д., Математика и правдоподобные рассуждения, пер. с англ., М., 1957; Давыдов В. В., Виды обобщения в обучении, М., 1972; Сачков Ю. В., Процессы обобщения в синтезе знаний, в кн.: Синтез современного научного знания, М., 1973, с. 421-46; Матюшкин А. М., Новосёлов М. М., Виды обобщения и проблемы психологии обучения, «Вопросы психологии», 1974, № 2. Ф. В. Лазарев, М. М. Новосёлов. Обобщённые импульсы
Обобщённые и'мпульсы, физические величины
p
i, определяемые формулами:
p
i=
Обобщённые координаты Обобщённые координа'ты, независимые между собой параметры q i( r= 1, 2,..., s) любой размерности, число которых равно числу sстепеней свободы механич. системы и которые однозначно определяют положение системы. Закон движения системы в О. к. даётся sуравнениями вида q i= q i( t) ,где t- время. О. к. пользуются при решении многих задач, особенно когда система подчинена связям, налагающим ограничения на её движение. При этом значительно уменьшается число уравнений, описывающих движение системы, по сравнению, например, с уравнениями в декартовых координатах (см. Лагранжа уравнения в механике). В системах с бесконечно большим числом степеней свободы (сплошные среды, физические поля) О. к. являются особые функции пространственных координат и времени, называются потенциалами, волновыми функциями и т.п. Обобщённые силы Обобщённые си'лы, величины, играющие роль обычных сил, когда при изучении равновесия или движения механической системы её положение определяется обобщёнными координатами . Число О. с. равно числу s степеней свободы системы; при этом каждой обобщённой координате q iсоответствует своя О. с. Q i. Значение О. с. Q i, соответствующей координате q i, можно найти, вычислив элементарную работу dA 1всех сил на возможном перемещении системы, при котором изменяется только координата q i, получая приращение dq 1. Тогда dA 1= Q 1dq 1, т.е. коэффициент при dq iв выражении dA 1и будет О. с. Q 1. Аналогично вычисляются Q 2, Q 3,..., Q s. Например, если для лебёдки ( рис. ) вместе с поднимаемым ею на тросе грузом весом Р (система с одной степенью свободы) принять за обобщённую координату q iугол j поворота вала лебёдки и если к валу приложены вращающий момент М ври момент сил трения М тр, то в данном случае dA 1= ( М вр-М тр-Pr)dj, где r - радиус вала (весом троса пренебрегаем). Следовательно, для этой системы О. с., соответствующей координате j, будет Q 1=М вр-М тр- Pr. Размерность О. с. зависит от размерности обобщённой координаты. Если размерность q i-длина, то Q iимеет размерность обычной силы; если q i-угол, то Q iимеет размерность момента силы и т.д. При изучении движения механической системы О. с. входят вместо обычных сил в Лагранжа уравнения механики, а при равновесии все О. с. равны нулю. Например, для рассмотренной выше лебёдки при равномерном подъёме груза должно быть Q i= 0, т. е. М вр= М тр+ Pr. С. М. Тарг. 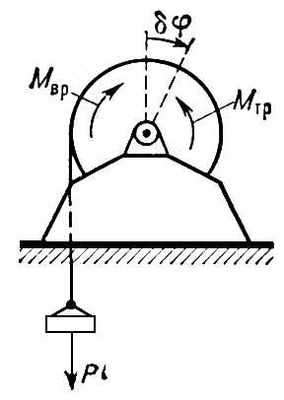
Рис. к ст. Обобщённые силы. Обобщённые функции Обобщённые фу'нкции, математическое понятие, обобщающее классическое понятие функции . Потребность в таком обобщении возникает во многих физических и математических задачах. Понятие О. ф., с одной стороны, даёт возможность выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки (пространственная), плотность простого или двойного слоя, интенсивность мгновенного источника и т.д. С другой стороны, в понятии О. ф. находит отражение тот факт, что реально нельзя измерить значение физич. величины в точке, а можно измерять лишь её средние значения в достаточно малых окрестностях данной точки. Таким образом, О. ф. служат удобным аппаратом для описания распределений различных физических величин. Поэтому в иностранной литературе О. ф. называют распределениями. О. ф. были введены впервые в конце 20-х гг. 20 в. П. Дираком в его исследованиях по квантовой механике, где он систематически использует понятие дельта-функции и её производных. Основы математической теории О. ф. были заложены С. Л. Соболевым в 1936 при решении Коши задачи для гиперболич. уравнений, а в послевоенные годы французский математик Л. Шварц дал систематическое изложение теории О. ф. В дальнейшем теорию О. ф. интенсивно развивали многие математики, главным образом в связи с потребностями математической физики. Теория О. ф. имеет многочисленные применения и всё шире входит в обиход физика, математика и инженера. Формально О. ф. определяются как линейные непрерывные функционалы над тем или иным линейным пространством основных функций j(x). Основным пространством функций является, например, совокупность бесконечно дифференцируемых финитных функций, снабженная надлежащей сходимостью (или, точнее, топологией). При этом обычные локально суммируемые функции f (x)отождествляются с функционалами (регулярными О. ф.) вида ( f, j) = т f (x)j(x) dx. (1) Произвольная О. ф. fопределяется как функционал f’, задаваемый равенством (fў, j) = (f, jў). (2) При таком соглашении каждая О. ф. бесконечно дифференцируема (в обобщённом смысле). Равенство (2) в силу (1) есть не что иное, как обобщение формулы интегрирования по частям для дифференцируемых в обычном смысле функций f (x), так что в этом случае оба понятия производной совпадают. Сходимость на (линейном) множестве О. ф. вводится как слабая сходимость функционалов. Оказывается, что операция дифференцирования О. ф. непрерывна, а сходящаяся последовательность О. ф. допускает почленное дифференцирование бесконечное число раз. Вводятся и другие операции над О. ф., например свёртка функций , Фурье преобразование , Лапласа преобразование . Теория этих операций приобретает наиболее простую и законченную форму в рамках понятия О. ф., расширяющих возможности классического математического анализа. Поэтому использование О. ф. существенно расширяет круг рассматриваемых задач и к тому же приводит к значительным упрощениям, автоматизируя элементарные операции. Примеры. 1) d-функция Дирака: (d, j) = j(0), описывает плотность массы (заряда) 1, сосредоточенной в точке х= 0, единичный импульс. 2) q (x) - функция Хевисайда: q(x) = 0, х Ј 0, q(x) = 1, x > 0, q' = d; производная от неё равна единичному импульсу. 3) -d' - плотность диполя момента 1 в точке х= 0, ориентированного вдоль оси х. 4) md s- плотность простого слоя на поверхности S с поверхностной плотностью m:
5)
6) Свёртка
-ньютонов потенциал с плотностью f, где f -любая О. ф. [например, из 1), 3), 4) и 5)]. 7) Общее решение уравнения колебаний струны
задаётся формулой u (х, t)= f (x+ at)+ g (x- at), где fи g- любые О. ф. Лит.:Дирак П. А. М., Основы квантовой механики, пер. с англ., М.-Л., 1932; Soboleff S., Mйthode nouvelle б resoudre le problйme de Cauchy pour les йquations lineaires hyperboliques normales, «Математический сборник», 1936, т. 1 (43), № 1 (резюме на рус. яз.); Schwartz L., Thйorie des distributions, t. 1-2, P., 1950-51; Гельфанд И. М., Шилов Г. Е., Обобщённые функции и действия над ними, 2 изд., М., 1959; Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971. В. С. Владимиров. Обобществление средств производства Обобществле'ние средств произво'дствав переходный период от капитализма к социализму, революционное преобразование частнокапиталистической собственности на средства производства в социалистическую общественную собственность и организация на этой основе нового типа общественного производства, планомерно обеспечивающего всё более полное благосостояние и свободное всестороннее развитие всех членов общества. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 |
|||||||
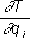 или
p
i=
или
p
i=
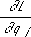 , где
Т- кинетическая энергия, a
L- Лагранжа функция данной механической системы, зависящие от обобщённых координат
q
i, обобщённых скоростей
, где
Т- кинетическая энергия, a
L- Лагранжа функция данной механической системы, зависящие от обобщённых координат
q
i, обобщённых скоростей
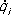 , и времени
t. Размерность О. и. зависит от размерности обобщённой координаты. Если размерность
q
i- длина, то
p
iимеет размерность обычного импульса, т. е. произведения массы на скорость; если же координатой
q
iявляется угол (величина безразмерная), то
p
iимеет размерность момента количества движения и т.д.
, и времени
t. Размерность О. и. зависит от размерности обобщённой координаты. Если размерность
q
i- длина, то
p
iимеет размерность обычного импульса, т. е. произведения массы на скорость; если же координатой
q
iявляется угол (величина безразмерная), то
p
iимеет размерность момента количества движения и т.д.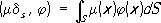
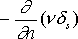 - плотность двойного слоя на поверхности S с поверхностной плотностью момента n диполей, ориентированных вдоль направления нормали
n:
- плотность двойного слоя на поверхности S с поверхностной плотностью момента n диполей, ориентированных вдоль направления нормали
n: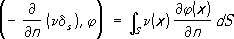 .
.