 |
|
Популярные авторы:: Азимов Айзек :: Раззаков Федор :: Борхес Хорхе Луис :: Лесков Николай Семёнович :: Верн Жюль Габриэль :: Станюкович Константин Михайлович :: Дю Понсон :: Чехов Антон Павлович :: Толстой Лев Николаевич :: Грин Александр Популярные книги:: Таинственное наследство :: Справочник по реестру Windows XP :: The Boarding House :: Космо Хилл. Супернатуралист :: Дюна (Книги 1-3) :: Книгоиздание в современной России :: Тегеран – Ялта – Потсдам :: На грани отчаяния :: Reality Dysfunction — Emergence :: Демон ростом два сантиметра |
Большая Советская Энциклопедия (ЛИ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ЛИ) - Чтение (стр. 24)
Линия (в генетике) Ли'нияв генетике, размножающиеся половым путём родственные организмы, которые происходят, как правило, от одного предка или одной пары общих предков и воспроизводят в ряду поколений одни и те же наследственно устойчивые признаки. Характерные для Л. признаки искусственно поддерживаются путём отбора и близкородственного скрещивания. Различают чистые линии - генотипически однородное потомство самоопыляющихся растений, у которых почти все гены находятся в гомозиготном состоянии, и инбредные Л. - потомство перекрёстноопыляющегося растения, полученное путем принудительного самоопыления, или группа животных, полученная при близкородственном разведении (см. Инбридинг ) .Чем теснее родство родителей, тем выше степень гомозиготности потомства. И в чистых, и в инбредных Л. постоянно возникающие мутации нарушают гомозиготность. Поэтому для сохранения гомозиготности по генам, определяющим основные свойства Л., необходимо вести отбор. В животноводстве различают генеалогическую Л., т. е. группу животных, происходящую от общего предка, и заводскую Л. - однородную, качественно своеобразную, поддерживаемую отбором и подбором с использованием инбридинга группу высокопродуктивных животных, происходящую от выдающегося родоначальника и схожую с ним по конституции и продуктивности (см. Разведение по линиям ) .Чистые и инбредные Л. служат основой для получения высокопродуктивных гибридов в растениеводстве и животноводстве. В медико-биологических исследованиях важную роль играют Л. лабораторных животных,сохраняющие константность по определённым признакам. Лит.:Иогансен В. Л., О наследовании в популяциях и чистых линиях, пер. с нем., М. - Л., 1935; Медведев Н. Н., Практическая генетика, М., 1966. Ю. С. Демин, Е. Я. Борисенко. Линия (геометрич. понятие) Ли'ния(от лат. linea), геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной геометрии рассматриваются прямые Л., отрезки прямых, ломаные Л., составленные из отрезков, и некоторые кривые Л. Каждый вид кривых Л. определяется тем или иным специальным способом (например, окружность определяется как геометрическое место точек, имеющих заданное расстояние R от заданной точки О - центра окружности). Иногда в учебниках дают определение Л. как границы куска поверхности (поверхность определяется при этом как граница тела) или как траектории движущейся точки. Но в рамках элементарной геометрии эти определения не получают отчётливой формулировки. 2) Представление о Л. как траектории движущейся точки может быть сделано вполне строгим при помощи идеи параметрического представления Л. Например, вводя на плоскости прямоугольные координаты ( x, у), можно параметрически задать окружность радиуса R с центром в начале координат уравнениями x = R cos t, y = R sin t. Когда параметр tпробегает отрезок 0 Ј tЈ 2p, точка ( х, у) описывает окружность. Вообще, Л. на плоскости задают параметрическими уравнениями вида
x =j (
t)
, у =
где j (
t)
,
Аналогично, в трёхмерном пространстве Л. задаётся параметрически тремя уравнениями вида
x =j (
t)
, у =
где j (
t)
,
P =j ( t) , где j - функция действительного переменного t, непрерывная на каком-либо интервале, значения которой суть точки пространства Т. Считают, что два параметрических представления задают одну и ту же Л., если они определяют один и тот же порядок следования её точек (в смысле, указанном выше). В анализе и топологии рассматривают обычно случай, когда область изменения параметра tесть отрезок аЈ tЈ b. В этом случае условие того, чтобы два параметрических представления Р =j ( t) , aЈ tЈ b P =j 1 ( t 1) , a 1Ј t 1Ј b 1, изображали одну и ту же Л., заключается в существовании непрерывной и строго возрастающей функции t 1= f( t) , для которой f( a) = a 1, f( b) = b 1,j ( t) =j 1[f( t) ]. Такое понимание термина «Л.» наиболее естественно в большинстве вопросов анализа (например, в теории криволинейных интегралов) и механики. Так как Л. здесь рассматривается вместе с порядком, в котором пробегает её точки переменная точка М при возрастании t, то при этом естественно возникает вопрос о числе прохождений переменной точки Л. через какую-либо точку пространства. Кроме простых точек, проходимых один раз, Л. может иметь кратные точки, которые проходятся несколько раз (отвечающие различным значениям параметра). Например, при изменении tв пределах - Ґ < t< Ґ точка с координатами
описывает строфоиду (см. рис. «Алгебраические кривые третьего порядка», № 5 ), попадая в положение х= 0, у= 0 два раза при t= - 1 и t= + 1. 3) Из аналитической геометрии известен и другой способ задания Л. на плоскости уравнением F( x, y) = 0; в пространстве - двумя уравнениями F( x, у, z) = 0, G( x, y, z) = 0. Ограничиваясь случаем плоскости, укажем лишь, как строится понятие алгебраической Л. (кривой) - Л., определяемой уравнением F( x, y) = 0, где F( x, у) - целая алгебраическая функция,т. е. многочлен како-либо степени n³ 1. В этом случае считают, что два многочлена F 1( x, у) и F 2( x, у) определяют одну и ту же алгебраическую Л. в том и только в том случае, когда существует такая постоянная с ¹ 0, что выполняется тождественно соотношение F 1( x, y) = cF 2( x, у) . Таким образом, все многочлены, определяющие одну и ту же Л., имеют одну и ту же степень n, называемую порядком соответствующей Л. Например, в аналитической геометрии принято считать, что уравнение ( х - у) 2 = 0 определяет Л. второго порядка, а именно, дважды взятую прямую х - у= 0. В связи с последним примером необходимо заметить, однако, что часто целесообразно ограничиваться рассмотрением неприводимых алгебраических Л., т. е. таких Л., для которых многочлен не допускает представления F = GH, где G и Н - отличные от постоянных многочлены. Далее, в пункте 4, имеется в виду только этот случай. Говорят, что точка ( x 0, y 0) кривой F( x, у) = 0 имеет кратность m, если разложение F( x, у) по степеням x = х - x 0, h = у - y 0начинается с членов степени m(по совокупности переменных x и h). В случае m= 2, т. е. в случае двойной точки F( x, у) = а 11( х - x 0) 2+ 2а 12( х - x 0) ( у - y 0) + a 22( y - y 0) 2+ ..., где многоточие означает, что далее следуют члены высших порядков. При помощи дискриминанта d = a 11a 22- а 12 2 можно определить тип двойной точки (см. Особые точки ) . 4) Часто, особенно при изучении алгебраической Л., целесообразно стать на точку зрения комплексной проективной геометрии, т. е. рассматривать, наряду с точками евклидовой действительной плоскости (или пространства), точки бесконечно удалённые и мнимые. Только при таком подходе (и надлежащем учёте кратности пересечения) становится верным, например, утверждение, что две Л. порядков nи mпересекаются в mn точках. В случае m= 1 это приводит к возможности определить порядок Л. как число nточек её пересечения с прямой. С проективной точки зрения естественно задавать Л. на плоскости однородным уравнением F( x 1, x 2, x 3) = 0 между однородными координатами x 1, x 2, x 3её точек. В силу принципа двойственности с этим заданием равноправно задание Л. уравнением F(x 1, x 2, x 3) = 0, связывающим однородные координаты прямых, касающихся Л. Таким образом, наряду с порядком Л. (степенью уравнения F = 0) естественно возникает понятие класса Л. - степени уравнения F = 0. Класс алгебраических Л. можно также определить как число касательных, которые можно провести к Л. из произвольной точки. О параметрическом представлении Л. см. также Уникурсальные кривые. 5) Рассмотренные выше (в пунктах 2-4) уточнения и обобщения понятия Л. существенно связаны с соответствующим алгебраическим и аналитическим аппаратом. В отличие от этого, современная топология выдвинула задачу уточнения представления о Л. как о множестве точек, независимо от алгебраического или аналитического способов задания этого множества. Если исходить из параметрического задания Л. в виде непрерывной функции P =j ( t), где tпробегает отрезок аЈ tЈ b, но интересоваться только полученным множеством точек без учёта порядка их следования, то приходят к понятию Л., сформулированному в 80-x гг. 19 в. К. Жорданом (см. Жордана кривая ) .Оказывается, что таким непрерывным образом отрезка может быть любой локально связный континуум, в частности квадрат, треугольник, куб и т. п. (см. Пеано кривая ) .Поэтому теперь обычно предпочитают говорить не о Л. в смысле Жордана, а о локально связных, или жордановых, континуумах. Взаимно однозначный непрерывный образ отрезка называют простой дугой, или жордановой дугой. Взаимно однозначный непрерывный образ окружности называют простой замкнутой Л. Простые дуги и простые замкнутые Л. не исчерпывают, однако, точечных множеств, заслуживающих наименования Л. Избегая и чрезмерной общности, и чрезмерного сужения понятия Л., в современной топологии пользуются понятием Л., введённым в 1921 П. С. Урысоном,который определяет Л. (кривую) как произвольный континуум размерности единица. Континуум имеет размерность единица, если при любом e > 0 он может быть представлен в виде суммы конечного числа замкнутых множеств диаметра, меньшего e, обладающих тем свойством, что никакие три из этих замкнутых множеств не имеют общей точки (см. также Размерность в геометрии). Континуум, лежащий на плоскости, будет Л. в смысле Урысона тогда и только тогда, когда он не содержит внутренних точек. Этим свойством характеризовал ранее (70-е гг. 19 в.) Л., лежащие на плоскости, Г. Кантор.Хотя определение Кантора применимо только к Л., лежащим на плоскости, иногда и общие Л. в смысле Урысона называют «канторовыми кривыми». Л. Н. Колмогоров. 6) Ещё математики древности изучали линии второго порядка ( эллипс, гиперболуи параболу ) .Ими же был рассмотрен ряд отдельных замечательных алгебраических Л. более высокого порядка, а также некоторые трансцендентные (неалгебраические) Л. Систематическое изучение Л. и их классификация стали возможными с созданием аналитической геометрии (Р. Декарт ) . Из Л. третьего порядка наиболее известны: Декартов лист (см. рис. «Алгебраические кривые третьего порядка», № 1 ). уравнение в прямоугольных координатах: x 3+ y 3- 3аху= 0. Впервые кривая определяется в письме Р. Декарта к П. Ферма в 1638. Полная форма кривой с наличием асимптоты, проходящей через точки ( - а, 0) и (0, - а), была определена позднее (1692) Х. Гюйгенсом и И. Бернулли.Название «декартов лист» установилось в начале 18 в. Локон Аньези (см. рис. «Алгебраические кривые третьего порядка», № 2 ). Пусть имеется круг с диаметром OC = - аи отрезок BDM, построенный так, что ОВ : BD = OC : ВМ; геометрическое место точек М представляет собой локон Аньези (или верзиеру). уравнение в прямоугольных координатах: у = a 3/( a 2+ x 2). Исследование этой Л. связано с именем итальянской женщины-математика Марии Аньези (1748). Кубическая парабола (см. рис. «Алгебраические кривые третьего порядка», № 3 ). уравнение в прямоугольных координатах: у = x 3. Полукубическая парабола (см. рис. «Алгебраические кривые третьего порядка», № 4 ), парабола Нейля. уравнение в прямоугольных координатах: у = -сх 3/2. Названа по имени английского математика У. Нейля (1657), нашедшего длину её дуги. Строфоида (от греч. strуphos - кручёная лента и йidos - вид) (см.
рис. «Алгебраические кривые третьего порядка», № 5
). Пусть имеется неподвижная прямая АВ и точка С вне её на расстоянии CO =
а; вокруг С вращается прямая, пересекающая АВ в переменной точке N. Если от точки N отложить по обе стороны прямой АВ отрезки NM = NM' = NO, то геометрическое место точек М и М' для всех положений вращающегося луча CN и есть строфоида. Уравнение в прямоугольных координатах:
Циссоида Диоклеса (см. рис. «Алгебраические кривые третьего порядка», № 6 ) (греч. kissoeides, от kissуs - плющ и йidos - вид), геометрическое место точек М, для которых OM = PQ (Р - произвольная точка производящего круга с диаметром а). Уравнение в прямоугольных координатах: y 2= х 3/( а - х); в полярных координатах: r = asin 2j/cos j. Древние греки рассматривали только ту часть циссоиды, которая находится внутри производящего круга. Вместе с дугой окружности эта часть образует фигуру, напоминающую лист плюща (откуда название); наличие бесконечных ветвей было установлено в 17 в. французским математиком Ж. П. Робервалем и независимо от него бельгийским математиком Р. Ф. Слюзом. Из Л. четвёртого и более высоких порядков наиболее известны: Кардиоида (от греч. kardнa - сердце и йidos - вид) (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 1 ), кривая, описываемая какой-либо точкой М окружности радиуса а, катящейся без скольжения по неподвижной окружности того же радиуса. уравнение в прямоугольных координатах: ( x 2+ y 2- 2ах) 2= 4a( x 2+ y 2); в полярных координатах: r = 2а (1 + cos j). Конхоида Никомеда (от греч. konchoeides - похожий на раковину) (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 2 ), кривая, получающаяся при увеличении или уменьшении каждого радиус-вектора точек данной прямой на одну и ту же величину d, т. о., OM = OP - dили OM' = OP + d. Если расстояние от полюса О до данной прямой равно а, то уравнение в прямоугольных координатах: ( х - а) 2 ( х 2+ y 2) - d 2x 2= 0, в полярных координатах: r = a/cosj ± d. Впервые рассматривалась древнегреческим геометром Никомедом (около 250-150 до нашей эры), который использовал её для решения задач о трисекции угла и удвоении куба. Лемниската Бернулли (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 3 ) (от лат. lemniscatus, буквально - украшенный лентами), кривая, имеющая форму восьмёрки; геометрическое место точек, произведение расстояний которых от фокусов F 1( - а, 0) и F 2( а, 0) равно а 2. уравнение в прямоугольных координатах: ( x 2+ y 2) 2- 2a 2( x 2- y 2) =0, в полярных координатах: r 2= 2а 2cos 2j. Впервые рассматривалась Я. Бернулли (1694). Лемниската является частным случаем овалов Кассини и синус-спиралей. Овалы Декарта (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 4 ), геометрические места точек М, расстояния которых от двух фиксированных точек F 1и F 2, называемых фокусами, умноженные на данные числа, имеют постоянную сумму с, то есть mMF 1+ + nMF 2= с. уравнение в прямоугольных координатах: ( x + y’’ -2rx) 2- l 2( x 2+ y 2) - k= 0, где r, lи k- некоторые постоянные, связанные с параметрами m, nи d; в полярных координатах: ( n 2- m 2)( 2+ 2(( mc - n2d cos() + n 2d 2- с 2= 0. Помимо фокусов F 1и F 2, имеется и третий фокус F 3, равноправный с каждым из них. При m= 1, n= 1 овал Декарта превращается в эллипс; при m= 1 и n= -1 - в гиперболу. Частным случаем овала является также улитка Паскаля. Овалы впервые исследовались Р. Декартом (1637). Овалы Кассини (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 5 ), геометрические места точек М, произведение расстояний которых от двух данных точек постоянно. Пусть F 1и F 2точки на оси абсцисс, F 1F 2= 2 b, а произведение MF 1ЧMF 2= а 2. уравнение в прямоугольных координатах: ( x 2+ y 2) 2- 2b 2( a 2- y 2) = a 4- b 4.
Если
Улитка Паскаля (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 6 ), геометрическое место точек М и M', расположенных на прямых пучка (центр которого О лежит на окружности радиуса R) на расстоянии а по обе стороны от точки Р пересечения прямых с окружностью; т. о., PM = PM' = а. уравнение в прямоугольных координатах: ( x 2+ y 2- 2Rx) 2- а 2( х 2+ y 2) = 0, в полярных координатах: r = 2 Rcos j + а. При а =2 Rпетля стягивается в точку, в этом случае улитка Паскаля превращается в кардиоиду. Название по имени французского учёного Э. Паскаля (1588-1651), впервые изучавшего её. Астроида (от греч. бstron - звезда и йidos - вид) (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 7 ), кривая, описываемая точкой подвижной окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. уравнение в прямоугольных координатах: x 2/3+ y 2/3= а 2/3, где а- радиус неподвижной окружности. Астроида - линия 6-го порядка. Розы (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 8 ), кривые, полярное уравнение которых: r = asin mj; если m- рациональное число, то розы - алгебраической Л. чётного порядка. При mнечётном роза состоит из от лепестков, при mчётном - из 2 mлепестков; при mрациональном лепестки частично покрывают друг друга. Синусоидальные спирали, синус-спирали (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 9 ), кривые, полярное уравнение которых r m= a mcos mj; если m- рациональное число, то эти Л. - алгебраические. Частные случаи: m= 1 - окружность, m= - 1 - прямая, m= 2 - лемниската Бернулли, m= -2 - равнобочная гипербола, m= 1/ 2- кардиоида, m= - 1/ 2- парабола. При целом m> 0 Л. состоит из m лепестков, каждый из которых лежит внутри угла, равного p/ m, при рациональном m> 0 лепестки могут частично покрывать друг друга; если m< 0, то Л. состоит из от бесконечных ветвей. Большой интересный класс составляют трансцендентные Л. К ним относятся графики тригонометрических функций (синусоида, тангенсоида), логарифмической функции, показательной функции, гиперболических функций,а также следующие Л.: Квадратриса (см.
рис. «Трансцендентные кривые», № 1
). Пусть прямая MN равномерно вращается против часовой стрелки вокруг точки О, а прямая А'В' равномерно движется справа налево, оставаясь параллельной OC. Далее, пусть за время движения A'B' от AB до OC прямая MN поворачивается на прямой угол и переходит из положения OA =
rв положение OC. Геометрическое место точек Р пересечения прямых MN и A'B' и есть квадратриса. уравнение в прямоугольных координатах:
Трактриса (см. рис. «Трансцендентные кривые», № 2 ), кривая, для которой длина отрезка касательной от точки касания М до точки Р пересечения с данной прямой есть величина постоянная, равная а. Уравнение в прямоугольных координатах:
Цепная линия (см.
рис. «Трансцендентные кривые», № 3
), кривая, форму которой принимает гибкая однородная и нерастяжимая тяжёлая нить, концы которой закреплены в двух точках. уравнение в прямоугольных координатах:
у = a
Циклоида (от греч. kykloeides - кругообразный) (см. рис. «Трансцендентные кривые», № 4 ), кривая, которую описывает точка Р, расположенная на расстоянии а от центра круга радиуса r, катящегося без скольжения по прямой линии. Если Р лежит на окружности круга ( r = а), получают обыкновенную циклоиду (см. рис. «Трансцендентные кривые», № 4а ), если она лежит внутри круга ( r > а), - укороченную циклоиду (см. рис. «Трансцендентные кривые», № 4б ), если точка вне круга ( r < а), - удлинённую циклоиду (см. рис. «Трансцендентные кривые», № 4в ). Две последние Л. называют трохоидами. Уравнение в параметрической форме:
Среди трансцендентных Л. особый класс составляют спирали (от греч. spйira, буквально - витое), плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь к ней или с каждым обходом удаляясь от неё. Если выбрать эту точку за полюс системы координат, то полярное уравнение спирали r = f(j) таково, что f(j + 2p) > f(j) или f(j + 2p) < f(j) при всех j. Из спиралей наиболее известны: Архимедова спираль (см. рис. «Трансцендентные кривые», № 5 ), кривая, описываемая точкой, равномерно движущейся по прямой в то время, как эта прямая равномерно вращается в плоскости вокруг точки О. уравнение в полярных координатах: r = aj, где а - постоянная. Эта спираль изучалась Архимедом (3 в. до н. э.) в связи с задачами трисекции угла и квадратуры круга. Гиперболическая спираль (см. рис. «Трансцендентные кривые», № 6 ), кривая, описываемая точкой М, движущейся по вращающейся прямой OA, так, что её расстояние от центра вращения меняется обратно пропорционально углу поворота. Уравнение в полярных координатах: r = а/j. Жезл (см.
рис. «Трансцендентные кривые», № 7
), кривая, уравнение которой в полярных координатах:
Логарифмическая спираль (см. рис. «Трансцендентные кривые», № 8 ), кривая, уравнение которой в полярных координатах: r = ае к j. Была известна многим математикам 17 в. Спираль Корню (см. рис. «Трансцендентные кривые», № 9 ), клотоида, кривая, состоящая из двух ветвей, симметричных относительно начала координат. уравнение в параметрической форме:
Использовалась французским физиком М. А. Корню (1874) для графич. решения некоторых задач дифракции света. Si-ci-спираль (см. рис. «Трансцендентные кривые», № 10 ), кривая, параметрическое уравнение которой имеет вид
si( t) и ci( t) - интегральный синус и интегральный косинус. К циклоиде по способу построения примыкает класс циклоидальных кривых, которые могут быть как алгебраическими, так и трансцендентными. Среди них: Гипоциклоида (см. рис. «Циклоидальные кривые», № 1а, 1б ) ,кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности внутри её. Уравнение в параметрической форме:
где А - радиус неподвижной, а а- подвижной окружности. Вид кривой зависит от отношения А/а. Эпициклоида (см. рис. «Циклоидальные кривые», № 2а, 2б ), кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности вне её. Уравнение получится из уравнения гипоциклоиды заменой ана - а. Удлинённая гипоциклоида (эпициклоида), кривая, описываемая точкой, лежащей вне окружности, которая катится без скольжения по другой окружности внутри (вне) её (см. рис. «Циклоидальные кривые», № 3а, 4д ). Аналогично определяется укороченная гипоциклоида (эпициклоида) (см. рис. «Циклоидальные кривые», № 3б, 4б ). Удлинённые и укороченные гипоциклоиды и эпициклоиды иногда называются гипо- и эпитрохоидами. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59 |
|||||||
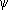 (
t)
,
(
t)
,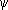 (
t) - произвольные функции, непрерывные на каком-нибудь конечном или бесконечном интервале D числовой оси
t. С каждым значением параметра
t(из интервала D) уравнения (*) сопоставляют некоторую точку M, координаты которой определяются этими уравнениями. Л., заданная параметрическими уравнениями (*) есть множество точек, соответствующих всевозможным значениям
tиз D, при условии, что эти точки рассматриваются в определенном порядке, именно: если точка
M
1соответствует значению параметра
t
1, а точка
M
2- значению
t
2, то
M
1считается предшествующей
M
2, если
t
1< t
2При этом точки, отвечающие различным значениям параметра, всегда считаются различными.
(
t) - произвольные функции, непрерывные на каком-нибудь конечном или бесконечном интервале D числовой оси
t. С каждым значением параметра
t(из интервала D) уравнения (*) сопоставляют некоторую точку M, координаты которой определяются этими уравнениями. Л., заданная параметрическими уравнениями (*) есть множество точек, соответствующих всевозможным значениям
tиз D, при условии, что эти точки рассматриваются в определенном порядке, именно: если точка
M
1соответствует значению параметра
t
1, а точка
M
2- значению
t
2, то
M
1считается предшествующей
M
2, если
t
1< t
2При этом точки, отвечающие различным значениям параметра, всегда считаются различными. (
t)
, z =c (
t)
,
(
t)
, z =c (
t)
,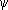 (
t)
,c (
t) - произвольные функции, непрерывные на каком-нибудь интервале. В произвольном
топологическом пространстве
Т (которое, в частности, может быть плоскостью, поверхностью, обычным трёхмерным пространством, функциональным пространством и т. п.) Л. параметрически задают уравнением вида
(
t)
,c (
t) - произвольные функции, непрерывные на каком-нибудь интервале. В произвольном
топологическом пространстве
Т (которое, в частности, может быть плоскостью, поверхностью, обычным трёхмерным пространством, функциональным пространством и т. п.) Л. параметрически задают уравнением вида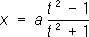 ,
,
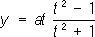
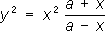 ; в полярных координатах: r = -a cos 2j/cosj. Впервые строфоиду исследовал Э.
Торричелли
(1645), название было введено в середине 19 в.
; в полярных координатах: r = -a cos 2j/cosj. Впервые строфоиду исследовал Э.
Торричелли
(1645), название было введено в середине 19 в.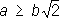 , то овал Кассини - выпуклая кривая; если
b<
a<
, то овал Кассини - выпуклая кривая; если
b<
a<
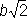 , то кривая имеет вид овала с двумя утолщениями; при
а = bовал Кассини превращается в лемнискату, наконец, при
b > аовал Кассини является двусвязной кривой. Впервые рассмотрена Дж.
Кассини
(17 в.).
, то кривая имеет вид овала с двумя утолщениями; при
а = bовал Кассини превращается в лемнискату, наконец, при
b > аовал Кассини является двусвязной кривой. Впервые рассмотрена Дж.
Кассини
(17 в.).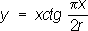 ; в полярных координатах:
; в полярных координатах:
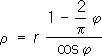 . Часть квадратрисы, заключённая в квадрате OABC, была известна древнегреч. математикам. Открытие квадратрисы приписывается Гиппию Элидскому (5 в. до н. э.), использовавшему её для решения задачи о трисекции угла. Динострат (4 в. до н. э.) с помощью квадратрнсы выполнил квадратуру круга.
. Часть квадратрисы, заключённая в квадрате OABC, была известна древнегреч. математикам. Открытие квадратрисы приписывается Гиппию Элидскому (5 в. до н. э.), использовавшему её для решения задачи о трисекции угла. Динострат (4 в. до н. э.) с помощью квадратрнсы выполнил квадратуру круга.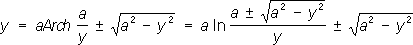 .
. = а(
e
x/a+ е
-х/a)
/2.
= а(
e
x/a+ е
-х/a)
/2. ,
,
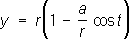 .
.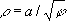 . Каждому значению j соответствуют два значения r - положительное и отрицательное. Кривая состоит из двух ветвей, каждая из которых асимптотически приближается к полюсу.
. Каждому значению j соответствуют два значения r - положительное и отрицательное. Кривая состоит из двух ветвей, каждая из которых асимптотически приближается к полюсу.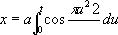 , y = a
, y = a
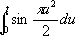 .
.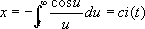 ,
, ,
,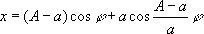 ,
,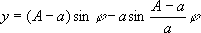 ,
,