 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (ЛИ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ЛИ) - Чтение (стр. 21)
a ij- постоянные. Линейные преобразования и переход от одной системы координат к другой в векторном пространстве осуществляются Л. п. Линейная поляризация Лине'йная поляриза'ция, состояние распространяющейся электромагнитной волны (например, световой), при котором её электрический вектор Е в каждой точке пространства, занятого волной, совершая колебания, остаётся всё время в одной и той же плоскости, проходящей через направление распространения волны (то же справедливо и по отношению к магнитному вектору волны Н). См. Поляризация света. Линейная система Лине'йная систе'мав музыке, система параллельных горизонтальных линий для записи нот; см. Нотное письмо. Линейная тактика Лине'йная та'ктика, теория и практика подготовки и ведения боя в линейных боевых порядках при равномерном распределении войск (сил флота) по фронту, существовавшая в 17-18 вв. Получила развитие в связи с оснащением армий огнестрельным оружием и повышением роли огня в бою. Войска для ведения боя располагались в линию, состоявшую из нескольких шеренг (их количество определялось в зависимости от скорострельности оружия), что позволяло одновременно вести огонь из наибольшего количества ружей. Тактика войск сводилась в основном к фронтальному столкновению. Исход сражения во многом решался мощью пехотного огня. Л. т. в Западной Европе зародилась в конце 16 - начале 17 вв. в нидерландской пехоте, где квадратные колонны были заменены линейными построениями. В русских войсках элементы Л. т. впервые были применены в сражении при Добрыничах (1605). Полное оформление Л. т. получила в шведской армии Густава II Адольфа в период Тридцатилетней войны 1618-1648,а затем была принята во всех европейских армиях. Этому способствовало увеличение скорострельности мушкета и усовершенствование артиллерии. Густав II Адольф увеличил число мушкетёров до 2/ 3состава своей пехоты, полностью отказался от глубоких построений и перешёл к строю в 6 и менее шеренг. Превосходство линейного боевого порядка над старым боевым порядком из колонн окончательно определилось в сражениях при Брейтенфельде (1631) и Лютцене (1632), но одновременно выявились и отрицательные стороны Л. т.: невозможность сосредоточения превосходящих сил на решающем участке боя, способность действовать только на открытой равнинной местности, слабость флангов и трудность осуществления маневра пехоты, в силу чего решающее значение для исхода боя приобрела кавалерия. Наёмные солдаты удерживались в сомкнутых линиях с помощью палочной дисциплины, а при нарушении строя убегали с поля боя. Классические формы Л. т. получила в 18 в., особенно в прусской армии Фридриха II, который жесточайшей муштрой довёл боевую скорострельность каждой линии до 2-3 залпов в минуту. Чтобы устранить недостатки Л. т., Фридрих II ввёл косой боевой порядок (батальоны наступали уступом), состоявший из 3 линий батальонов, имевших по 3 шеренги. Конница строилась в 3 линии. Артиллерия размещалась в интервалах между батальонами, на флангах и впереди боевого порядка. Несмотря на достигнутое совершенство, Л. т. войск Фридриха II продолжала оставаться шаблонной и негибкой. Русские полководцы 18 в. - Петр I, П. С. Салтыков, П. А. Румянцев, А. В. Суворов, придерживаясь Л. т., искали новые способы ведения боя. Петр I в линейном боевом порядке создавал резерв, Румянцев начал применять рассыпной строй и каре. Суворов наряду с линейным боевым порядком ввёл колонны, применял каре, рассыпной строй и сочетание всех этих форм боевого построения войск. К концу 18 в. Л. т. исчерпала свои возможности, французская, русская, затем и др. армии перешли к новой тактике, основанной на сочетании колонн и рассыпного строя. (См. Военное искусство.) Л. т. до конца 18 в. господствовала также и в ВМФ. Корабли для ведения морского боя строились в линию, исход боя решался фронтальным столкновением и одновременным ведением огня из орудий большинства кораблей. В конце 18 в. в ВМФ перешли к новой - манёвренной тактике, основы которой были заложены русскими адмиралами Г. А. Спиридовым и Ф. Ф. Ушаковым. (См. Военно-морское искусство.) В современных условиях термин «Л. т.» обычно употребляется, когда имеются в виду неповоротливые боевые порядки, отсутствие их глубины, равномерное распределение сил по фронту, неспособность к маневру с изменением обстановки и др. И. И. Картавцев. Линейная форма Лине'йная фо'рма, форма первой степени. Общий вид Л. ф. n переменных x 1, x 2, ..., x n: f( x 1, x 2, ..., x n) = a 1x 1+a 2x 2+ ... + a nx n, где a 1, а 2, ..., a n- постоянные. Если x 1, x 2, ..., x nтрактовать как координаты вектора хв n-мерном векторном пространстве,то f удовлетворяет условию f(a x +b у) =a f( x) +b f( y) (где х, у- векторы, a ,b - числа), которое может быть принято за определение. Линейная функция Лине'йная фу'нкция, функция вида у = kx + b. Основное свойство Л. ф.: приращение функции пропорционально приращению аргумента. Графически Л. ф. изображается прямой линией. При равных масштабах на осях коэффициент k; (угловой коэффициент) равен тангенсу угла, образованного прямой с осью Ox ( k= tg j, см. рис .), а b- отрезку, отсекаемому прямой на оси Оу. При b= 0 Л. ф. называется однородной; её график изображает пропорциональную зависимость: у = kx. Л. ф. широко применяется в физике и технике для представления (нередко - приближённо) зависимостей между различными величинами. Рассматривают также Л. ф. многих переменных; однородные Л. ф. многих переменных называют линейными формами.Если и аргумент и функция суть векторы, то однородными Л. ф. являются линейные преобразования. 
Рис. к ст. Линейная функция. Линейная эрозия Лине'йная эро'зия, размыв горных пород и почв водой, текущей по устойчивым руслам; Л. э. приводит к образованию рытвин, оврагов, балок, долин. См. Эрозия. Линейного интерполирования метод Лине'йного интерполи'рования ме'тод, один из методов приближённого вычисления корней уравнения (трансцендентного или алгебраического) f( x) = 0. Сущность Л. и. м. заключается в следующем. Исходя из двух близких к корню а значений x 0и x 1, в которых функция f( x) принимает значения разных знаков, берут в качестве следующего приближённого значения x 2корня a точку пересечения с осью абсцисс прямой, проходящей через точки ( x 0, f( x 0)) и( x 1, f( x 1)) (см. рис .). Повторяя эту процедуру на более узком интервале [ х 0, x 2], находят следующее приближение x 3и т. д. Общая формула Л. и. м. имеет вид
Др. названия Л. и. м.: метод хорд, метод секущих и (устаревшее) правило ложного положения (Regula faisi). Лит.:Березин И. С.. Жидков Н. П., Методы вычислений, 2 изд., т. 2, М., 1962. 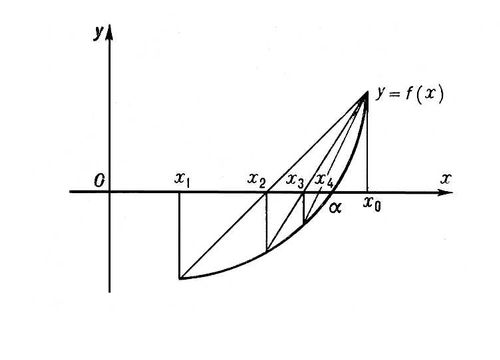
Рис. к ст. Линейного интерполирования метод. Линейное письмо Лине'йное письмо'А и Б, древнейшие письменности о. Крита. В текстах, выполненных Л. п. Б (крито-микенским слоговым письмом), засвидетельствован один из диалектов древнегреческого языка. Надписи, датируемые 15-14 вв. до н. э. и найденные в конце 19 в. на о. Крите, были впервые опубликованы английским учёным А. Эвансом в 1909. В 1939 в южной части Пелопоннеса были найдены таблички с такими же надписями, относящимися примерно к 13 в. до н. э. Дешифровка Л. п. Б принадлежит английским учёным М. Вентрису и Дж. Чедвику (1953). Знаки крито-микенского письма, соответствующие отдельным гласным или группам, состоящим из согласного с последующим гласным, по мнению некоторых учёных, были, очевидно, заимствованы и приспособлены к нуждам греческого языка. Некоторые знаки совпадают со знаками кипрского слогового письма (6-2 вв. до н. э.) и Л. п. А, которое датируется примерно 18-15 вв. до н. э. Не поддающееся дешифровке Л. п. А, по всей вероятности, не является индоевропейским (см. Критское письмо ) .
Лит.:Георгиев В., Словарь крито-микенских надписей, София, 1955; Лурье С. Я., Язык и культура микенской Греции, М., 1957; Furumark A., Linear A und die altkretische Sprache, B., 1956; Meriggi P., Primi elementi di minoico A, Salamanca. 1956; Sundwall J., Minoische Beitrдge, «Minos», 1955, № 3, 1956, № 4; Chadwick J., Ventris M Studies in Mycenaean inscriptions and dialect, L., 1956; их же, Documents in Mycenaean Greek, Camb., 1956; «Minoica», B., 1958; Peruzzi E., Le iscrizioni minoiche, Firenze, 1960. М. Л. Воскресенский. Линейное преобразование Лине'йное преобразова'ниепеременных x 1, x 2, ..., x n- замена этих переменных на новые x' 1, x’ 2, ..., x' n, через которые первоначальные переменные выражаются линейно, т. е. по формулам: x 1= a 11x’ 1+ a 12x’ 2+ ... + a nnx’ n+ b 1, x 2= a 21x’ 1+ a 22x’ 2+ ... + a 2nx’ n+ b 2, ... x n= a n1x’ 1+ an2x’ 2+ ... + a nnx’ n+ b n, здесь a ijи b i( i, j= 1,2, ..., n) - произвольные числовые коэффициенты. Если b 1, b 2,..., b nвсе равны нулю, то Л. п. переменных называют однородным. Простейшим примером Л. п. переменных могут служить формулы преобразования прямоугольных координат на плоскости х = x' cosa - y' sina + a, у = x' sina + y' cosa + b. Если определительD= ½ a ij½, составленный из коэффициентов при переменных, не равен нулю, то можно и новые переменные x' 1, x' 2, ..., x' nлинейно выразить через старые. Например, для формул преобразования прямоугольных координат
и x’ =x cosa + ysina + a 1 y’ = -x sina + cosa + b 1 где a 1= - a cosa - b sina , b 2= a sina - b cos( .Другими примерами Л. п. переменных могут служить преобразования аффинных и однородных проективных координат, замена переменных при преобразовании квадратичных форм и т. п. Л. п. векторов (или Л. п. векторного пространства ) называют закон, по которому вектору хиз n-мерного пространства ставят в соответствие новый вектор x', координаты которого линейно и однородно выражаются через координаты вектора х: x’ 1= a 11x 1+ a 12x 2+ ... +a 1nx n x’ 2= a 21x 1+ a 22x 2+ ... +a 2nx n ... x’ n= a n1x 1+ a n2x 2+ ... +a nnx n, или коротко x' = Ax. Например, операция проектирования на одну из координатных плоскостей (пусть на плоскость хОу) будет Л. п. трёхмерного векторного пространства: каждому вектору ас координатами х, у, zсопоставляется новый вектор b, координаты x', y'., z'которого выражаются через х, у, zследующим образом : x' = х, y' = у, z'= 0. Пример Л. п. плоскости - поворот её на угол a вокруг начала координат. Матрицу
составленную из коэффициентов Л. п. А, называют его матрицей. Матрицами приведённых выше Л. п. проектирования и поворота будут соответственно
Л. п. векторного пространства можно определить (как обычно поступают) без использования системы координат: соответствие х® у= Ax называют Л. п., если выполняются условия А( х + у) = Ax + Ау и A(a x) =a А( х) для любых векторов хи уи любого числа a. В разных системах координат одному и тому же Л. п. будут соответствовать разные матрицы и, следовательно, разные формулы для преобразования координат. К Л. п. относится, в частности, нулевое Л. п. О, переводящее все векторы в 0 (нулевой вектор) : Ox= 0и единичное Л. п. Е, оставляющее все векторы без изменения: Ex= х; этим Л. и. в любой системе координат соответствуют нулевая и единичная матрицы. Для Л. п. векторного пространства естественным образом определяются операции сложения и умножения: суммой двух Л. п. А и В называют Л. п. С, переводящее любой вектор хв вектор Cx = Ax + Вх;произведением Л. п. А и В называют результат их последовательного применения: С = AB, если Cx = А( В х) .
В силу этих определений совокупность всех Л. п. векторного пространства образует
кольцо.Матрица суммы (произведения) Л. п. равна сумме (произведению) матриц Л. п. слагаемых (сомножителей); при этом существен порядок множителей, так как произведение Л. и., как и матриц, не обладает свойством
коммутативности.Л. п. можно также умножать на числа: если Л. п.
Апереводит вектор
хв вектор
у=
Ax,то a
Апереводит
хв a
у. Примеры операций над Л. п.: 1) Пусть
Аи
Возначают операции проектирования па оси Ox и Оу в трёхмерном пространстве;
А + Вбудет проектированием на плоскость хОу, а
AB= 0. 2)
Аи
В- повороты плоскости вокруг начала координат на углы j и
Л. п.
Вназывают обратным к Л. п.
А(и обозначают
А
-1), если
BA = Е(или
AB = Е). Если Л. п.
Апереводило вектор х в вектор у, то Л. п.
А
-
1переводит у обратно в х. Л. п., обладающее обратным, называют невырожденным; такие Л. п. характеризуются также тем, что определитель их матрицы не равен нулю. Некоторые классы Л. п. заслуживают особого упоминания. Обобщением поворотов двумерных и трёхмерных евклидовых пространств являются ортогональные (или унитарные - в комплексных пространствах) Л. п. Ортогональные Л. п. не изменяют длин векторов (а следовательно, и углов между ними). Матрицы этих Л. п. в ортонормированной системе координат также называются ортогональными (унитарными): произведение ортогональной матрицы на её транспонированную даёт единичную матрицу: е
ka
ika
jk= е
ka
kia
kj= 0 при i ¹ j, е
ka
2
ik= е
ka
2
ki= 1 (в комплексном пространстве е
ka
ik
Приведённое выше определение Л. п. в векторном пространстве, не использующее координатную систему, без всяких изменений распространяется и на бесконечномерные (в частности, функциональные) пространства. Л. п. в бесконечномерных пространствах принято называть линейными операторами.
Лит.:Александров П. С., Лекции по аналитической геометрии..., М., 1968; Мальцев А. И., Основы линейной алгебры, 3 изд., М., 1970; Ефимов Н. В., Розендорн Э. P., Линейная алгебра и многомерная геометрия, М., 1970. Линейное программирование Лине'йное программи'рование, математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах, задаваемых системами линейных неравенств и равенств; Л. п. является одним из разделов математического программирования. Типичным представителем задач Л. п. является следующая: найти максимум линейной функции
при условиях
x j³ 0, j= 1, 2, n, (3) где c j, a ijи b i- заданные величины. Задачи Л. п. являются математическими моделями многочисленных задач технико-экономического содержания. Рассмотрим в качестве примера следующую задачу планирования работы предприятия. Для производства однородных изделий необходимо затратить различные производственные факторы - сырьё, рабочую силу, станочный парк, топливо, транспорт и т. д. Обычно имеется несколько отработанных технологических способов производства, причём в этих способах затраты производственных факторов в единицу времени для выпуска изделий различны. Количество израсходованных производственных факторов и количество изготовленных изделий зависит от того, сколько времени предприятие будет работать по тому или иному технологическому способу. Ставится задача рационального распределения времени работы предприятия по различным технологическим способам, т. е. такого, при котором будет произведено максимальное количество изделий при заданных ограниченных затратах каждого производственного фактора. Формализуем задачу. Пусть имеется nтехнологических способов производства изделий и mпроизводственных факторов. Введём обозначения: c j- количество изделий, выпускаемых в единицу времени при работе по j-му технологическому способу; a ij- расход i-го производственного фактора в единицу времени при работе по j-му технологическому способу; b i- имеющиеся ресурсы i-го производственного фактора и x j- планируемое время работы по j-му технологическому способу. Величина
означает общий расход i-го производственного фактора при плане
х
(
i)
=(
x
(
i)
1, x
(
i)
2, ..., x
(
i)
n
)
.И поскольку ресурсы ограничены величинами b
i, то возникают естественные условия (2) и (3). Ставится задача отыскания такого распределения времени (оптимального плана)
х* =(
x*
1, х*
2, ..., х*
n) работы по каждому технологическому способу, при котором общий объём продукции
Термин «Л. п.» нельзя признать удачным, однако смысл его в том, что в Л. п. решаются задачи составления оптимальной программы (плана) действий. В связи с этим Л. п. можно рассматривать как один из математических методов в исследованиях операций (см. Операций исследование ) . Функцию (1) в Л. п. принято называть целевой функцией, или критерием эффективности, вектор х =( x 1, x 2, ..., x n) - планом, вектор x*=( x* 1, x* 2, ..., x* n) - оптимальным планом, а множество, определяемое условиями (2) - (3), - допустимым, или множеством планов. Одним из основных методов решения задач Л. п. является симплексный метод. Геометрически его идея состоит в следующем. Допустимое множество (2) - (3) представляет собой выпуклое многогранное множество (если оно ограничено, то - многомерный выпуклый многогранник). Если задача Л. п. имеет решение, то существует вершина х*многогранного множества, являющаяся оптимальным планом. Симплексный метод состоит в таком направленном переборе вершин, при котором значение целевой функции возрастает от вершины к вершине. Каждой вершине соответствует система уравнений, выбираемая спец. образом из системы неравенств (2) - (3), поэтому вычислительная процедура симплексного метода состоит в последовательном решении систем линейных алгебраических уравнений. Простота алгоритма делает этот метод удобным для его реализации на ЭВМ. Лит.:Юдин Д. Б., Гольштейн Е. Г., Линейное программирование, М., 1969. В. Г. Карманов. Линейное пространство
Лине'йное простра'нство, тоже, что
векторное пространство.В
функциональном анализе
рассматриваются главным образом бесконечномерные пространства. Примером бесконечномерного Л. п. может служить пространство всех многочленов (с вещественными или комплексными коэффициентами) при обычном определении сложения и умножения на числа. Одним из первых примеров бесконечного Л. п. были
гильбертово пространство
и пространство С [
а, b] непрерывных функций, заданных на отрезке [
а, b]. Эти пространства являются нормированными, т. е. такими Л. п., в которых введена норма элемента
х- неотрицательное число
В конечномерном пространстве различные нормы топологически равносильны: последовательность точек, сходящихся при одной норме, сходится и при любой другой. В бесконечномерных пространствах нормы могут быть существенно различны. Например, при решении задачи П. Л. Чебышева о разыскании многочлена, наименее уклоняющегося от нуля (задачи о наилучшем приближении), надо найти такой многочлен ( k- 1)-й степени P k-i( t), чтобы
имел наименьшее значение. Вводя в пространство С[0,1] норму формулой
эту задачу можно сформулировать следующим образом: требуется найти многочлен P k -i( t), расстояние которого от функции t*было бы наименьшим. При рассмотрении же многочленов, ортогональных с весом p(t) (см. Ортогональная система функций ) ,естественно рассматривать норму, определённую формулой
и решать задачу о наилучшем приближении в смысле этой нормы. Нормы
по первой норме расходится, а по второй норме при p( t) = 1 сходится к функции
Следует отметить, что хотя все функции
x
n(
t) были непрерывны, функция
x(
t) разрывна. Это связано с тем, что пространство непрерывных функций неполно относительно нормы
существует в Л. п. такой элемент х, что данная последовательность сходится к нему, т. е.
Если Л. п. неполно, то к нему можно присоединить новые элементы (пополнить его) так, что оно станет полным. Например, пополняя пространство непрерывных функций, взятое с нормой
Обобщением понятия B-пространства является понятие топологического Л. п. Так, называют множество Е, если: 1) оно представляет собой Л. п., 2) оно является топологическим пространством,3) операции сложения и умножения на числа в Енепрерывны относительно заданной в Етопологии. К числу топологического Л. п. относятся все нормированные пространства. А. Н. Колмогоров установил (1934) необходимые и достаточные условия нормируемости топологического Л. п. Лит.:Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965. Линейное судоходство Лине'йное судохо'дство, см. Морские линии. Линейное уравнение Лине'йное уравне'ние, уравнение, в которое неизвестные входят в 1-й степени (т. е. линейно) и отсутствуют члены, содержащие произведения неизвестных. Несколько Л. у. относительно одних и тех же неизвестных образуют систему Л. у. Решением системы Л. у. называют набор чисел c 1, c 2, ..., c n, обращающих все уравнения в тождества после подстановки их вместо соответствующих неизвестных. Система Л. у. может иметь как одно единственное решение, так и бесконечное множество решений (неопределённая система); может также оказаться, что система Л. у. не имеет ни одного решения (несовместная система). Чаще всего встречается случай, когда число уравнений совпадает с числом неизвестных. Одно Л. у. с одним неизвестным имеет вид: ax = b; решением его при а¹ 0 будет число b/a. Система двух Л. у. с двумя неизвестными имеет вид:
где a 11, a 12, a 21, a 22, b 1, b 2- какие-либо числа. Решение системы (1) можно получить с помощью определителей:
здесь предполагается, что стоящий в знаменателе определитель
Аналогичное правило применимо и при решении любой системы и Л. у. с nнеизвестными, т. е. системы вида: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59 |
|||||||
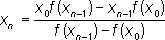 , (
n= 2, 3, ...).
, (
n= 2, 3, ...).
 ,
, и
и
 .
. ; AB будет поворотом на угол j +
; AB будет поворотом на угол j +
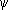 . 3) Произведение единичного Л. п. Е на число a будет преобразованием подобия с коэффициентом растяжения (или сжатия) a.
. 3) Произведение единичного Л. п. Е на число a будет преобразованием подобия с коэффициентом растяжения (или сжатия) a. jk= е
ka
ki
jk= е
ka
ki
 kj= 0, е
k|a
jk|
2= е
k|a
ki|
2= 1). Симметрическим (эрмитовым, или самосопряжённым, - в комплексном пространстве) Л. п. называют такое Л. п., матрица которого симметрическая: a
ij= a
ji(или (a
ij=
kj= 0, е
k|a
jk|
2= е
k|a
ki|
2= 1). Симметрическим (эрмитовым, или самосопряжённым, - в комплексном пространстве) Л. п. называют такое Л. п., матрица которого симметрическая: a
ij= a
ji(или (a
ij=
 ij). Симметрические Л. п. осуществляют растяжение пространства с разными коэффициентами по неск. взаимно ортогональным направлениям. С симметрическими Л. п. связана теория квадратичных форм (или эрмитовых форм в комплексном пространстве).
ij). Симметрические Л. п. осуществляют растяжение пространства с разными коэффициентами по неск. взаимно ортогональным направлениям. С симметрическими Л. п. связана теория квадратичных форм (или эрмитовых форм в комплексном пространстве).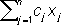 (1)
(1) ,
i= 1, 2, ...,
m, (2)
,
i= 1, 2, ...,
m, (2)
 был бы максимальным, то есть задача (1) - (3). Другим характерным примером прикладных задач Л. п. является
транспортная задача.
был бы максимальным, то есть задача (1) - (3). Другим характерным примером прикладных задач Л. п. является
транспортная задача. , обращающееся в нуль лишь при
х= 0 и обладающее свойствами
, обращающееся в нуль лишь при
х= 0 и обладающее свойствами
 и
и
 (неравенство треугольника). Число
(неравенство треугольника). Число
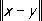 называют расстоянием между элементами
хи
у(см. также
Метрическое пространство
)
.В нормированном Л. п. вводятся понятия открытого шара, предельной точки множества, непрерывности функционала аналогично тому, как это делается в трёхмерном пространстве.
называют расстоянием между элементами
хи
у(см. также
Метрическое пространство
)
.В нормированном Л. п. вводятся понятия открытого шара, предельной точки множества, непрерывности функционала аналогично тому, как это делается в трёхмерном пространстве.
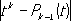
 =
=

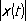
 ,
, и
и
 существенно различны, так как, например, последовательность функций
существенно различны, так как, например, последовательность функций
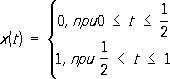 .
.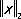 . При этом нормированное Л. п. называется полным, если для любой последовательности {
x
n} его элементов, удовлетворяющих условию
. При этом нормированное Л. п. называется полным, если для любой последовательности {
x
n} его элементов, удовлетворяющих условию ,
,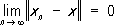 ,
,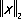 , получают гильбертово пространство
L
2
p. Полные нормированные Л. п. называется банаховыми, или В-пространствами, - по имени изучившего их основные свойства С.
Банаха.
, получают гильбертово пространство
L
2
p. Полные нормированные Л. п. называется банаховыми, или В-пространствами, - по имени изучившего их основные свойства С.
Банаха. (1)
(1) ,
,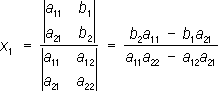 ;
; отличен от нуля. В числителях стоят определители, получающиеся из
Dзаменой в нём одного столбца столбцом свободных членов
b
1, b
2; в выражении для первого неизвестного
x
1заменяется первый столбец, а в выражении для второго неизвестного
x
2- второй.
отличен от нуля. В числителях стоят определители, получающиеся из
Dзаменой в нём одного столбца столбцом свободных членов
b
1, b
2; в выражении для первого неизвестного
x
1заменяется первый столбец, а в выражении для второго неизвестного
x
2- второй.