 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (ЛА)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ЛА) - Чтение (стр. 26)
Лапла'с(Laplace) Пьер Симон (23.3.1749, Бомон-ан-Ож, Нормандия, - 5.3.1827, Париж), французский астроном, математик и физик, член Парижской АН (1785, адъюнкт с 1773), член Французской академии (1816). Учился в школе бенедиктинцев, из которой вышел, однако, убеждённым атеистом. В 1766 Л. приехал в Париж, где Ж. Д'Аламбер через пять лет помог ему получить место профессора Военной школы. Деятельно участвовал в реорганизации системы высшего образования во Франции, в создании Нормальной и Политехнической школ. В 1790 Л. был назначен председателем Палаты мер и весов, руководил введением в жизнь новой метрической системы мер. С 1795 в составе руководства Бюро долгот. Научное наследие Л. относится к области небесной механики, математики и математической физики, фундаментальными являются работы Л. по дифференциальным уравнениям, в частности по интегрированию методом «каскадов» уравнений с частными производными. Введённые Л. имеют разнообразные применения. В алгебре Л. принадлежит важная теорема о представлении определителей суммой произведений дополнительных миноров. Для разработки созданной им математической теории вероятностей Л. ввёл так называемые и широко применял преобразование, носящее его имя (см. ) .Теория вероятностей явилась основой для изучения всевозможных статистических закономерностей, в особенности в области естествознания. До него первые шаги в этой области были сделаны Б. ,П. ,Я. и др. Л. привёл их выводы в систему, усовершенствовал методы доказательств, сделав их менее громоздкими; доказал теорему, носящую его имя (см. ) ,развил теорию ошибок и способ наименьших квадратов, позволяющие находить наивероятнейшие значения измеренных величин и степень достоверности этих подсчётов. Классический труд Л. «Аналитическая теория вероятностей» издавался трижды при его жизни - в 1812, 1814 и 1820; в качестве введения к последним изданиям была помещена работа «Опыт философии теории вероятностей» (1814), в которой в популярной форме разъясняются основные положения и значение теории вероятностей. Вместе с А. Л. в 1779-84 занимался физикой, в частности вопросом о скрытой теплоте плавления тел и работами с созданным ими ледяным калориметром. Для измерения линейного расширения тел они впервые применили зрительную трубу; изучали горение водорода в кислороде. Л. активно выступал против ошибочной гипотезы о .Позднее снова вернулся к физике и математике. Он опубликовал ряд работ по теории капиллярности и установил закон, носящий его имя (см. ) .В 1809 Л. занялся вопросами акустики; вывел формулу для скорости распространения звука в воздухе. Л. принадлежит для вычисления изменения плотности воздуха с высотой над поверхностью земли, учитывающая влияние влажности воздуха и изменение ускорения свободного падения. Занимался также геодезией (см. , ) . Л. развил методы небесной механики и завершил почти всё то, что не удалось его предшественникам в объяснении движения тел Солнечной системы на основе закона всемирного тяготения Ньютона; ему удалось доказать, что закон всемирного тяготения полностью объясняет движение этих планет, если представить их взаимные возмущения в виде рядов. Он доказал также, что эти возмущения носят периодический характер. В 1780 Л. предложил новый способ вычисления орбит небесных тел. Исследования Л. доказали устойчивость Солнечной системы в течение очень длительного времени. Далее Л. пришёл к заключению, что кольцо Сатурна не может быть сплошным, т.к. в этом случае оно было бы неустойчиво, и предсказал открытие сильного сжатия Сатурна у полюсов. В 1789 Л. рассмотрел теорию движения спутников Юпитера под действием взаимных возмущений и притяжения к Солнцу. Он получил полное согласие теории с наблюдениями и установил ряд законов этих движений. Одной из главных заслуг Л. было открытие причины ускорения в движении Луны. В 1787 он показал, что средняя скорость движения Луны зависит от эксцентриситета земной орбиты, а последний меняется под действием притяжения планет. Л. доказал, что это возмущение не вековое, а долгопериодическое и что впоследствии Луна станет двигаться замедленно. По неравенствам в движении Луны Л. определил величину сжатия Земли у полюсов. Ему принадлежит также разработка динамической теории приливов. Небесная механика во многом обязана трудам Л., которые подытожены им в классическом сочинении «Трактат о небесной механике» (т. 1-5, 1798-1825). Космогоническая гипотеза Л. имела огромное философское значение (см. ) .Она изложена им в приложении к его книге «Изложение системы мира» (т. 1-2, 1796). По философским взглядам Л. примыкал к французским материалистам; известен ответ Л. Наполеону I, что в своей теории о происхождении Солнечной системы он не нуждался в гипотезе о существовании бога. Ограниченность механистического материализма Л. проявилась в попытке объяснить весь мир, в том числе физиологического, психического и социальные явления, с точки зрения механистического детерминизма. Своё понимание детерминизма Л. рассматривал как методологический принцип построения всякой науки. Образец окончательной формы научного познания Л. видел в небесной механике. Лапласовский детерминизм стал нарицательным обозначением механистической методологии классической физики. Материалистическое мировоззрение Л., ярко сказавшееся в научных трудах, контрастирует с его политической неустойчивостью. При всяком политическом перевороте Л. переходил на сторону победивших: сначала был республиканцем, после прихода к власти Наполеона - министром внутренних дел; затем был назначен членом и вице-председателя сената, при Наполеоне получил титул графа империи, а в 1814 подал свой голос за низложение Наполеона; после реставрации Бурбонов получил пэрство и титул маркиза. Соч.: Oeuvres.... t. 1-14, P., 1878-1912; в рус. пер. - Изложение системы мира., т. 1-2, СНБ, 1861; Опыт философии теории вероятностей, М., 1908. Лит.:Воронцов-Вельяминов Б. А., Лаплас, М., 1937. 
П. С. Лаплас. Лапласа азимут Лапла'са а'зимут, геодезический азимут А направления на наблюдаемую точку, полученный по его астрономическому азимуту a, исправленному с учётом влияния в пункте наблюдения. Астрономический азимут направления на какую-либо точку в пространстве есть двугранный угол между плоскостью астрономического меридиана пункта наблюдения и плоскостью, проходящей через отвесную линию в этом пункте и наблюдаемую точку. Л. а. (геодезический азимут) пространственной точки равен двугранному углу между плоскостью геодезического меридиана пункта наблюдения и плоскостью, проходящей через нормаль к поверхности в этом пункте и наблюдаемую точку. Для перехода от астрономич. азимута к Л. а. служит формула А = a- htgj - (xsina - hcosa)ctg z, в которой x и h - составляющие отклонения отвеса в пункте наблюдения в плоскостях меридиана и первого вертикала, j - широта этого пункта и z - зенитное расстояние наблюдаемой точки в пространстве. Эта формула при z, близком к 90°, приводит к уравнению Лапласа для определения Л. а.: a - А = htgj (назван по имени П. ,установившего это соотношение). Лит.:Красовский Ф. Н., Руководство по высшей геодезии, 2 изд., ч. 2, М., 1942. Л. А. Изотов. Лапласа гипотеза Лапла'са гипо'теза, космогоническая гипотеза об образовании Солнечной системы - Солнца, планет и их спутников из вращающейся и сжимающейся газовой туманности, высказанная П. в 1796 в популярной книге «Изложение системы мира» (т. 1-2). Согласно Л. г., в результате ускорения вращения при сжатии разряженная внешняя часть туманности (протяжённая атмосфера образующегося Солнца) становится всё более сплюснутой, а когда центробежная сила на экваторе стала равной по величине силе тяготения, она приняла чечевицеобразную форму. Вещество на остром ребре чечевицы перестало участвовать в дальнейшем сжатии, а оставалось на месте, образуя газовый диск. Затем он разделился на отдельные кольца и вещество каждого кольца собралось в сгусток, превратившийся затем в планету. При сжатии этих сгустков процесс зачастую повторялся, приводя к образованию спутников планет. Центральный сгусток туманности превратился в Солнце. Л. г. не смогла объяснить медленное вращение Солнца, прямое вращение планет, наличие спутников с обратным движением и спутников, период обращения которых меньше периода вращения планеты. Привлечение современных астрофизических данных позволило в середине 20 в. по-новому развить идею Лапласа об отделении вещества от сжимающегося протосолнца в результате наступления ротационной неустойчивости. При этом механизм формирования планет оказался отличным от предполагавшегося Лапласом. Л. г. сыграла выдающуюся роль в истории науки. См. . Б. Ю. Левин. Лапласа закон
Лапла'са зако'н, зависимость перепада гидростатического давления Dp на поверхности раздела двух фаз (жидкость - жидкость, жидкость - газ или пар) от межфазного поверхностного натяжения s и средней кривизны поверхности e в рассматриваемой точке: Dр=р
1- р
2= es, где p
1- давление с вогнутой стороны поверхности, p
2- с выпуклой стороны, e =
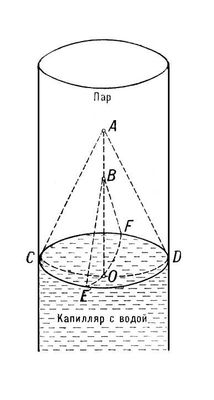
Применение закона Лапласа к поверхности раздела вода - пар в капилляре:
Лапласа неизменяемая плоскость Лапла'са неизменя'емая пло'скость, плоскость, проходящая через центр масс Солнечной системы перпендикулярно вектору момента количества движения. Понятие Л. н. п. было введено в 1789 П. ,указавшим на преимущества её использования в качестве основной координатной плоскости при изучении движений тел Солнечной системы: в то время как положения плоскостей эклиптики и экватора непрерывно изменяются, Л. н. п. сохраняет своё положение в пространстве неизменным. Для того чтобы определить положение Л. н. п. относительно плоскости эклиптики, необходимо знать числовые значения масс всех планет. Поскольку с развитием астрономических исследований эти величины постепенно уточняются, то и параметры, определяющие положение Л. н. п., несколько изменяются. Положение Л. п. п. относительно эклиптики в эпоху 1950,0 определяется следующими элементами: эклиптическая долгота точки пересечения с эклиптикой W = 107° 13,3' ± 2,1’, наклон i = 1°38'49’’± 22’’. Г. А. Чеботарев. Лапласа оператор Лапла'са опера'тор, лапласиан, дельта-оператор, D-оператор, линейный дифференциальный ,который функции j(x 1, x 2,..., x n) от n переменных x 1, x 2,..., x nставит в соответствие функцию Dj =
В частности, для функции j(x, y) двух переменных х, у Л. о. имеет вид Dj =
а для функций одной переменной j(x) Л. о. совпадает с оператором второй производной Dj =
Л. о. встречается в тех задачах математической физики, где изучаются свойства изотропной однородной среды (распространение света, тепла, движение идеальной несжимаемой жидкости и т.п.). Уравнение Dj = 0 обычно называется отсюда и произошло название Л. о. Лапласа преобразование Лапла'са преобразова'ние, преобразование, переводящее функцию f (t) действительного переменного t(0 < t< Ґ), называемую «оригиналом», в функцию
комплексного переменного р=s +it. Под Л. п. понимают также не только само преобразование, но и его результат - функцию F( p). Интеграл в правой части формулы (1) называется интегралом Лапласа. Он был рассмотрен П. в ряде работ, которые объединены в его книге «Аналитическая теория вероятностей», вышедшей в 1812. Значительно раньше (в 1737) такие интегралы применял к решению дифференциальных уравнений Л. . При некоторых условиях, указанных ниже, Л. п. определяет функцию f( t) однозначно, в простейших случаях - по формуле обращения:
Л. п. является линейным функциональным преобразованием. Из числа основных формул Л. п. можно отметить следующие:
Л. п. в сочетании с формулой (2) его обращения применяется к интегрированию дифференциальных уравнений. В частности, в силу свойства (1) и линейности, Л. п. решения обыкновенного линейного дифференциального уравнения с постоянными коэффициентами удовлетворяет алгебраическому уравнению 1-й степени и может быть, следовательно, легко найдено. Так, если, например, у’’ + у= f( t) , y(0) = y’(0) =0 и Y( p) = L [y], F( p) = L [f], то L [y’’] = p 2Y( p) и p 2Y( p) + Y( p) = F( p) , откуда
Многочисленные задачи электротехники, гидродинамики, механики, теплопроводности эффективно решаются методами, использующими Л. п. Л. п. нашло особенно широкое применение в обосновании ,в котором обычно вместо Л. п. F (p) вводится «изображение» оригинала f( t) - функция pF( p) . Современная общая теория Л. п. строится на основе интегрирования в смысле Лебега (см. ) .Для применимости Л. п. к функции f( t) необходимо, чтобы f( t) была интегрируема в смысле Лебега на любом конечном интервале (0, t), t> 0 и интеграл (1) для неё сходился хотя бы в одной точке p 0= s 0+ it 0. Если интеграл (1) сходится в точке р 0, то он сходится во всех точках р, для которых Re ( р-р 0) > 0. Т. о., если интеграл (1) сходится хотя бы в одной точке плоскости p 0, то либо он сходится во всей плоскости, либо существует такое число s с, что при Re p> s cинтеграл (1) сходится, а при Re р< s срасходится. Число s сназывается абсциссой сходимости интеграла Лапласа. F( p) - в полуплоскости Re р> s с .
Лит.:Диткин В. А. и Кузнецов П. И., Справочник по операционному исчислению. Основы теории и таблицы формул, М. - Л., 1951; Диткин В. А. и Прудников А. П., Интегральные преобразования и операционное исчисление, М., 1961; Дёч Г., Руководство к практическому применению преобразования Лапласа, пер. с нем., М., 1965. Лапласа теорема Лапла'са теоре'ма, простейшая из теории вероятностей, относящаяся к распределению отклонений частоты появления события при независимых испытаниях от его вероятности. В общем виде эта теорема доказана П. в книге «Аналитическая теория вероятностей» (1812). Один частный случай Л. т. был известен А. (1730), в связи с чем Л. т. иногда называется теоремой Муавра - Лапласа. Формулировка Л. т. такова. Пусть при каждом из n независимых испытаний вероятность появления некоторого события Е равна р(0< р<1) и пусть mобозначает число испытаний, в которых событие Е фактически наступает; тогда вероятность неравенства
при достаточно большом числе испытаний n сколь угодно мало отличается от
Если обозначить через X kслучайную величину, принимающую значение, равное 1, при появлении события Е в k-ом испытании и значение, равное 0, при его непоявлении, то m представляется как сумма независимых случайных величин m= X 1+ ...+ X n. Это позволяет рассматривать Л. т. как частный случай более общих предельных теорем теории вероятностей, в частности . Приближённые значения вероятностей, даваемые Л. т., на практике используются как точные при npqпорядка нескольких десятков и большем. Лит.см. при ст. теории вероятностей. Ю. В. Прохоров. Лапласа уравнение Лапла'са уравне'ние, дифференциальное уравнение с частными производными
где х, у, z- независимые переменные, а u = u( x, y, z) - искомая функция. Это уравнение названо по имени П. ,рассмотревшего его в работах по теории тяготения (1782). К Л. у. приводит ряд задач физики и техники. Л. у. удовлетворяют температура при стационарных процессах, потенциал электростатического поля в точках пространства, свободных от зарядов, потенциал поля тяготения в области, не содержащей притягивающих масс, и т. п. Функции, удовлетворяющие Л. у., называются .О постановке задач для Л. у. см. в ст. . Лапласов пункт Лапла'сов пункт, точка земной поверхности, обычно пункт триангуляции или полигонометри и, в котором широта, долгота и азимут определены как из астрономических наблюдений, так и по геодезическим измерениям, отнесённым к известной системе координат, связанной с с заданными размерами и положением в теле Земли. Между геодезическим и астрономическим азимутом и долготой существует зависимость, называется уравнением Лапласа (см. ) .Сопоставление астрономической широты, долготы и азимута с соответственными геодезическими величинами позволяет вывести в каждом Л. п. отклонения отвеса, которые характеризуют отклонение принятого земного эллипсоида от действительной фигуры Земли или несовпадение геодезической системы координат с системой астрономических координат, связанной с Землёй. В государственной геодезической сети СССР Л. п. принято определять через 150-200 км. Ла-Плата (город в Аргентине) Ла-Пла'та(La Plata) - город на В. Аргентины, на южном берегу залива Ла-Плата, административный центр провинции Буэнос-Айрес. 408,3 тыс. жителей (1970). Ж.-д. узел и важный морской порт по вывозу с.-х. продукции Пампы (зерно, мясо, шерсть, кожсырьё). Один из ведущих центров нефтеперерабатывающей и нефтехимической, а также мясохладобойной промышленности. Университет. Естественноисторический музей «Ла-Плата». Л.-П. основан в 1882. Ла-Плата (залив) Ла-Пла'та(исп. Rнo de la Plata, буквально - серебряная река), залив Атлантического океана у юго-восточного берега Южной Америки. Представляет собой эстуарий р. Парана. Длина 320 км,ширина до 220 км,глубина 10-20 м.Приливы неправильные, полусуточные, их величина до 1 м.На побережье Л.-П. - крупные города: Буэнос-Айрес (Аргентина) и Монтевидео (Уругвай). Лаплатская низменность Лапла'тская ни'зменность, название низменной восточной части равнин Парагвая - Параны (Центр, равнины) в Южной Америке (на востоке Гран-Чако и Пампы и в Междуречье). Простирается с С. на Ю. на 2400 км,с В. на З. на 900 км.Л. н. представляет собой синеклизу Южноамериканской платформы, заполненную мощной толщей континентальных, преимущественно кайнозойских, отложений. На С. тропический летневлажный климат, редколесья и обширные болота вдоль рек; на Ю. субтропический равномерновлажный климат, прерии и степи. Лапоноидная раса Лапоно'идная ра'са(от позднелат. Lapones - лапландцы и греч. йidos - вид, наружность), вариант .Характеризуется низким ростом, очень низким лицом, выступающими скулами, вогнутой спинкой носа, небольшим процентом .Представители Л. р. - саамы. Лаппаран Альбер Огюст Лаппара'н(Lapparent) Альбер Огюст (30.12.1839, Бурж, департамент Шер, - 5.5.1908, Париж), французский геолог, член Парижской АН (1897). Окончил Высшую горную школу в Париже (1864). Основные труды по различным вопросам геологии. Автор учебных руководств по геологии, минералогии и горючим полезным ископаемым, выдержавших несколько изданий. Принимал участие в составлении детальной геологические карты Франции. Соч.: Traitй de gйologie, 5 ed., [pt.] 1-3, P., 1906; La formation des combustibles minйraux, P., 1886. Лаппенранта Ла'ппенранта(фин. Lappeenranta), Вильманстранд (швед. Villmanstrand), город и порт в Финляндии, в ляни Кюми, на южном берегу оз. Сайма. 51 тыс. жителей (1970), включая поселок Лауритсала (судоверфи). Деревообрабатывающая, целлюлозно-бумажная, химическая (сернокислотная), цементная, пищевая промышленность. Лаппи Ла'ппи(Lappi), ляни (административная единица) на С. Финляндии. Площадь 93,9 тыс. км 2.Население 196 тыс. человек (1971). Административный центр - г. Рованиеми. Преобладают холмистые равнины и возвышенности. Наиболее крупная возвышенность - Манселькя. Густая сеть рек. Много озёр, наибольшее - Инари. Ландшафты северной тайги. Редко населённый и экономически мало освоенный район страны. Лесное хозяйство; очаги молочного животноводства и земледелия. На р. Кеми-Йоки каскады ГЭС. Лесозаготовки, лесопиление, деревообрабатывающая, целлюлозно-бумажная промышленность. Лаппо Иван Иванович Ла'ппоИван Иванович (1869-23.12.1944, Дрезден), русский историк. Родился в дворянской семье. В 1892 окончил историко-филологический факультет Петербургского университета. Профессор русской истории Тартуского (1905-19) и Каунасского (1933-40) университетов. В 1921-33 жил в Праге. Первое сочинение «Тверской уезд в XVI в. Его население и виды земельного владения» (1894) основано на статистической обработке данных писцовых книг. Большая часть сочинений Л. посвящена истории Великого княжества Литовского 16 в. (истории государственных учреждений и общественного строя, шляхетства и политической борьбы). Эти сочинения, богатые фактическим материалом, написаны в типичном для представителя государственной школы историко-юридическом духе. Соч.: Великое княжество Литовское за время от заключения Люблинской унии до смерти Стефана Батория, СПБ, 1901; Великое княжество Литовское во второй половине XVI ст. Литовско-русский повет и его сеймик, Юрьев, 1911; Западная Россия и её соединение с Польшей в их историческом прошлом, Прага, 1924; Идея единства русского народа в Юго-Западной Руси в эпоху присоединения Малороссии к Московскому государству, Прага, 1929. Лаппо-Данилевский Александр Сергеевич Ла'ппо-Даниле'вскийАлександр Сергеевич [15(27).1.1863, с. Удачное Верхнеднепровского у., ныне Днепропетровской области, - 7.2.1919, Петроград], русский историк, член Петербургской АН (1899); по политическим взглядам был близок к кадетам. Из дворян Екатеринославской губернии. В 1886 окончил историко-филологический факультет Петербургского университета; с 1890 приват-доцент, позднее профессор этого университета. Автор многих работ по социально-экономической и политической истории России периода феодализма, по методологии исторических основ русской археографии. Значительна деятельность Л.-Д. и его учеников («школа Л.-Д.») в области источниковедения и дипломатики, в частности в исследовании писцовых книг как исторических источников. Л.-Д. были подготовлены и изданы: «Кормленая книга Костромской чети 1613-1627», «Писцовая и переписная книги XVII в. по Нижнему Новгороду», «Записная книга крепостным актам XV-XVI вв., явленным в Новгороде дьяку Д. Алябьеву» - «Русская историческая библиотека» (т. 17, 1898); «Сборник грамот Коллегии экономии» (т. 1-2, 1922-29). В первые годы научной деятельности Л.-Д. примыкал к сторонникам государственной теории исторического процесса, разделял взгляды позитивистов. В начале 20 в., под влиянием работ немецкого философа и социолога Г. ,стал на позиции неокантианства, с позиций субъективного идеализма выступал против марксистского понимания истории, противопоставлял, в частности, естествознание, изучающее законы природы, исторической науке; придерживался взгляда, что историческое исследование источника должно вестись методами психологического, индивидуализирующего истолкования. Отрицая общественно-исторический критерий ценности источника, Л.-Д. считал основным проникновение в психологию автора источника. Труды Л.-Д., богатые фактическим материалом, сохранили научную ценность. Соч.: Скифские древности, СПБ, 1887; Критические заметки по истории народного хозяйства в Великом Новгороде и его области за XI-XV вв., СПБ. 1895; Организация прямого обложения в Московском государстве со времён Смуты до эпохи преобразований, СПБ, 1890; Очерк внутренней политики императрицы Екатерины II, СПБ, 1898; Русские промышленные и торговые компании в первой половине XVIII ст. Исторический очерк, СПБ. 1899; Очерк истории образования главнейших разрядов крестьянского населения в России, СПБ, 1905; Методология истории, в. [1]-2, СПБ, 1910-13; Очерк русской дипломатики частных актов, П., 1920. Лит.:Памяти академика А. С. Лаппо-Данилевского, «Русский исторический журнал», 1920, кн. 6 (имеется список науч. трудов Л.-Д.); Черепнин Л. В., А. С. Лаппо-Данилевский - буржуазный историк и источниковед, «Вопросы истории», 1949, № 8; Очерки истории исторической науки в СССР, т. 3, М., 1963. В. Н. Буганов. 
А. С. Лаппо-Данилевский. Лаппо-Данилевский Иван Александрович Ла'ппо-Даниле'вскийИван Александрович [16(28).10.1896, Петербург, - 15.3.1931, Гисен, Германия], советский математик, член-корреспондент АН СССР (1931). Сын А. С. .В 1925 окончил Ленинградский университет, работал в ряде ленинградских высших учебных заведений. Л.-Д. построил теорию функций от матриц и применил её к решению основных проблем теории линейных дифференциальных уравнений, что дало ему возможность получить ряд фундаментальных результатов. Соч.: Применение функций от матриц к теории линейных систем обыкновенных дифференциальных уравнений, М., 1957. Лапта Лапта', русская народная командная игра с мячом и битой. Упоминания о Л. встречаются в памятниках древнерусской письменности. Игра проводится на естественной площадке. Цель игры - ударом биты послать мяч, подбрасываемый игроком команды противника, как можно дальше и пробежать поочерёдно до противоположной стороны и обратно, не дав противнику «осалить» себя пойманным мячом. За удачные пробежки команде начисляются очки. Выигрывает команда, набравшая больше очков за установленное время. Игры, напоминающие Л., существуют в ряде др. стран, например , и др. Лаптев Дмитрий Яковлевич Ла'птевДмитрий Яковлевич (гг. рождения и смерти неизвестны), русский исследователь Арктики, вице-адмирал (1762). Начал службу на флоте в 1718 гардемарином. С 1736 руководил одним из северных отрядов Второй Камчатской экспедиции. В результате плаваний и сухопутных походов 1739-42 были проведены описи морского побережья от устья Лены до мыса Большой Баранов (к В. от устья р. Колыма), бассейна и устья р. Анадырь, пути по суше от Анадырского острога до Пенжинской губы. В 1741-42 Л. произвёл съёмку pp. Большой Анюй и Анадырь. По окончании экспедиции продолжал службу на Балтийском флоте. В 1762 уволен в отставку. Именем Л. названы: мыс в дельте Лены, пролив между о. Большой Ляховский и материком Азии. В честь Д. Я. и X. П. Лаптевых названо одно из морей Северного Ледовитого океана (море Лаптевых). Лаптев Константин Антонович Ла'птевКонстантин Антонович [родился 21. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45 |
|||||||
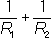 , R
1и R
2- радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности в данной точке (см.
рис
.). Л. з., установленный в 1806 П.
,определяет величину
и позволяет тем самым записать условия механического равновесия для подвижных (жидких) поверхностей раздела (см.
)
.
, R
1и R
2- радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности в данной точке (см.
рис
.). Л. з., установленный в 1806 П.
,определяет величину
и позволяет тем самым записать условия механического равновесия для подвижных (жидких) поверхностей раздела (см.
)
. р = р
1- p
2; R
1и R
2- радиусы кривизны в точке О вогнутой поверхности (R
1= ОА и R
2= ОВ) определяются в двух взаимно перпендикулярных сечениях ACD и BEF.
р = р
1- p
2; R
1и R
2- радиусы кривизны в точке О вогнутой поверхности (R
1= ОА и R
2= ОВ) определяются в двух взаимно перпендикулярных сечениях ACD и BEF. .
. ,
, .
. (1)
(1) (2)
(2) ,
,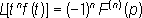 ,
n= 1, 2, …,
,
n= 1, 2, …,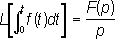 ,
t>0.
,
t>0.

 .
.