 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ИЗ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ИЗ) - Чтение (стр. 5)
ЧаСүРө РІСҒРөРіРҫ Рҳ. РҫРҝСҖРөРҙРөР»СҸСҺСӮ РҙР»СҸ РҫРұРҫРіР°СүРөРҪРҪРҫРіРҫ РҝСҖРҫРҙСғРәСӮР°: РәРҫРҪСҶРөРҪСӮСҖР°СӮР° , СҲСӮРөР№РҪР° Рё РҙСҖ. РҹСҖРё СҚСӮРҫРј СҖазлиСҮР°СҺСӮ СӮРҫРІР°СҖРҪРҫРө Рҳ., РҫРҝСҖРөРҙРөР»СҸРөРјРҫРө СҮРөСҖРөР· РҫСӮРҪРҫСҲРөРҪРёРө РјР°СҒСҒ РёР·РІР»РөРәР°РөРјРҫРіРҫ РәРҫРјРҝРҫРҪРөРҪСӮР° РІ СӮРҫРІР°СҖРҪРҫРј РҝСҖРҫРҙСғРәСӮРө Рё СҒСӢСҖСҢРө, Рё СӮРөС…РҪРҫР»РҫРіРёСҮРөСҒРәРҫРө Рҳ., РҫРҝСҖРөРҙРөР»СҸРөРјРҫРө РҝРҫ РәРҫРҪСҶРөРҪСӮСҖР°СҶРёСҸРј РәРҫРјРҝРҫРҪРөРҪСӮР° РІ РёСҒС…РҫРҙРҪРҫРј Рё РІСҒРөС… РәРҫРҪРөСҮРҪСӢС… РҝСҖРҫРҙСғРәСӮах СӮРөС…РҪРҫР»РҫРіРёСҮРөСҒРәРҫРіРҫ РҝСҖРҫСҶРөСҒСҒР°. Р Р°СҒС…РҫР¶РҙРөРҪРёРө РјРөР¶РҙСғ СӮРҫРІР°СҖРҪСӢРј Рё СӮРөС…РҪРҫР»РҫРіРёСҮРөСҒРәРёРј Рҳ. СғРәазСӢРІР°РөСӮ РҪР° РҪРөСӮРҫСҮРҪРҫСҒСӮСҢ Р°РҪализа РәРҫРҪСҶРөРҪСӮСҖР°СҶРёР№, СҒСғСүРөСҒСӮРІРҫРІР°РҪРёРө РјРөС…Р°РҪРёСҮРөСҒРәРёС… РҝРҫСӮРөСҖСҢ РІ СӮРөС…РҪРҫР»РҫРіРёСҮРөСҒРәРҫРј РҝСҖРҫСҶРөСҒСҒРө, РҪРөСӮРҫСҮРҪРҫСҒСӮСҢ РҫРҝСҖРҫРұРҫРІР°РҪРёСҸ. В РҹСҖРё РіРҫСҖРҪСӢС… СҖР°РұРҫСӮах РҫРҝСҖРөРҙРөР»СҸСҺСӮ Рҳ. Р·Р°РҝР°СҒРҫРІ РҝРҫР»РөР·РҪРҫРіРҫ РёСҒРәРҫРҝР°РөРјРҫРіРҫ РёР· РҪРөРҙСҖ РәР°Рә СҒСӮРөРҝРөРҪСҢ РҝРҫР»РҪРҫСӮСӢ РІСӢРөРјРәРё СҖСғРҙРҪРҫР№ РјР°СҒСҒСӢ, СғРіР»СҸ или РҪРөС„СӮРё РІ РҝСҖРҫСҶРөСҒСҒРө СҖазСҖР°РұРҫСӮРәРё РҙР°РҪРҪРҫРіРҫ РјРөСҒСӮРҫСҖРҫР¶РҙРөРҪРёСҸ. В Рӣ. Рҗ. БаСҖСҒРәРёР№. РҳР·РІР»РөСҮРөРҪРёРө РәРҫСҖРҪСҸ
РҳР·РІР»РөСҮРө'РҪРёРө РәРҫ'СҖРҪСҸ,алгРөРұСҖаиСҮРөСҒРәРҫРө РҙРөР№СҒСӮРІРёРө, РҫРұСҖР°СӮРҪРҫРө
РІРҫР·РІРөРҙРөРҪРёСҺ РІ СҒСӮРөРҝРөРҪСҢ
. РҳР·РІР»РөСҮСҢ РәРҫСҖРөРҪСҢ
n-Р№ СҒСӮРөРҝРөРҪРё РёР· СҮРёСҒла
Р°- СҚСӮРҫ Р·РҪР°СҮРёСӮ РҪайСӮРё СӮР°РәРҫРө СҮРёСҒР»Рҫ (или СҮРёСҒла)
x, РәРҫСӮРҫСҖРҫРө РҝСҖРё РІРҫР·РІРөРҙРөРҪРёРё РІ
n-СҺ СҒСӮРөРҝРөРҪСҢ РҙР°СҒСӮ РҙР°РҪРҪРҫРө СҮРёСҒР»Рҫ (
x
n=
Р°); СҮРёСҒР»Рҫ
С…(РҫРұРҫР·РҪР°СҮР°РөСӮСҒСҸ
В РӣРёСӮ.:Р‘СҖР°РҙРёСҒ Р’. Рң., Р§РөСӮСӢСҖёхзРҪР°СҮРҪСӢРө РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёРө СӮР°РұлиСҶСӢ, 41 РёР·Рҙ., Рң., 19703 БаСҖР»РҫСғ Рҹ., РўР°РұлиСҶСӢ РәРІР°РҙСҖР°СӮРҫРІ, РәСғРұРҫРІ, РәРІР°РҙСҖР°СӮРҪСӢС… РәРҫСҖРҪРөР№, РәСғРұРёСҮРөСҒРәРёС… РәРҫСҖРҪРөР№ Рё РҫРұСҖР°СӮРҪСӢС… РІРөлиСҮРёРҪ РІСҒРөС… СҶРөР»СӢС… СҮРёСҒРөР» РҙРҫ 12500, Рң., 1965. РҳР·РІРҫР°СҖРө РҳР·РІРҫР°'СҖРө(Izvoare), С…Рҫлм СҒ РҫСҒСӮР°СӮРәами РјРҪРҫРіРҫСҒР»РҫР№РҪРҫРіРҫ РҝРҫСҒРөР»РөРҪРёСҸ РҫРәРҫР»Рҫ Рі. РҹСҢСҸСӮСҖР°-РқСҸРјСҶ (Р СғРјСӢРҪРёСҸ). Р Р°СҒРәРҫРҝРәРё РІРөлиСҒСҢ РІ 1936-48. Р’ РәСғР»СҢСӮСғСҖРҪРҫРј СҒР»РҫРө РјРҫСүРҪРҫСҒСӮСҢСҺ 3 РјРІСӢРҙРөР»РөРҪСӢ 5 РіРҫСҖРёР·РҫРҪСӮРҫРІ РҪРөРҫ- Рё СҚРҪРөРҫлиСӮРёСҮРөСҒРәРҫРіРҫ РІСҖРөРјРөРҪРё. Р”СҖРөРІРҪРөР№СҲРёРө РҫСӮРҪРҫСҒСҸСӮСҒСҸ Рә РәСғР»СҢСӮСғСҖРө РҹСҖРөРәСғРәСғСӮРөРҪРё II-III (СҒРёРҪС…СҖРҫРҪРҪР° СҖР°РҪРҪРөР№ СӮСҖРёРҝРҫР»СҢСҒРәРҫР№ РәСғР»СҢСӮСғСҖРө ), РұРҫР»РөРө РҝРҫР·РҙРҪРёРө - Рә РәСғР»СҢСӮСғСҖам РҡСғРәСғСӮРөРҪРё Рҗ Рё Р“РҫСҖРҫРҙРёСҲСӮСҸ-РӯСҖРұРёСҮРөРҪСҢ (СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСӮ СҖазвиСӮРҫР№ Рё СҮР°СҒСӮРёСҮРҪРҫ РҝРҫР·РҙРҪРөР№ СӮСҖРёРҝРҫР»СҢСҒРәРҫР№ РәСғР»СҢСӮСғСҖРө). РқайРҙРөРҪСӢ жилиСүР°, РҝРҫСҒСғРҙР° СҒ РјРҫРҪРҫ- Рё РҝРҫлихСҖРҫРјРҪСӢРјРё СғР·РҫСҖами, РҫСҖСғРҙРёСҸ СӮСҖСғРҙР° РёР· РәамРҪСҸ, РәРҫСҒСӮРё Рё СҖРҫРіР°, фигСғСҖРәРё Р»СҺРҙРөР№ Рё живРҫСӮРҪСӢС…, РјРөРҙРҪСӢРө СғРәСҖР°СҲРөРҪРёСҸ. РӯРҪРөРҫлиСӮРёСҮРөСҒРәРёРө СҒР»РҫРё Рҳ. РҪР°СҖСғСҲРөРҪСӢ РұРҫРіР°СӮСӢРјРё РјРҫгилами 4 РІ. РҪ. СҚ. Рё СҒСҖРөРҙРҪРөРІРөРәРҫРІСӢРјРё РјРҫР»РҙавСҒРәРёРјРё РҝРҫРіСҖРөРұРөРҪРёСҸРјРё 14-17 РІРІ. В РӣРёСӮ.:Vulpe R., Izvoare. Spturile din 1937-1948, Buc., 1957. РҳР·РІРҫР»СҢСҒРәРёР№ РҗР»РөРәСҒР°РҪРҙСҖ РҹРөСӮСҖРҫРІРёСҮ РҳР·РІРҫ'Р»СҢСҒРәРёР№РҗР»РөРәСҒР°РҪРҙСҖ РҹРөСӮСҖРҫРІРёСҮ [6(18).3.1856, РңРҫСҒРәРІР°, - 16.8.1919, РҹР°СҖРёР¶], СҖСғСҒСҒРәРёР№ РіРҫСҒСғРҙР°СҖСҒСӮРІРөРҪРҪСӢР№ РҙРөСҸСӮРөР»СҢ, РҙРёРҝР»РҫРјР°СӮ. Р’ 1894-97 РјРёРҪРёСҒСӮСҖ-РҝСҖРөР·РёРҙРөРҪСӮ РІ Р’Р°СӮРёРәР°РҪРө, РІ 1897 РҝРҫСҒлаРҪРҪРёРә РІ Р‘РөлгСҖР°РҙРө, РІ 1897-99 РІ РңСҺРҪС…РөРҪРө, РІ 1899-1903 РІ РўРҫРәРёРҫ Рё РІ 1903-06 РІ РҡРҫРҝРөРҪгагРөРҪРө. Р’ 1906-10 РјРёРҪРёСҒСӮСҖ РёРҪРҫСҒСӮСҖР°РҪРҪСӢС… РҙРөР». РҹСҖРё РөРіРҫ СғСҮР°СҒСӮРёРё РұСӢли Р·Р°РәР»СҺСҮРөРҪСӢ: СҖСғСҒСҒРәРҫ-Р°РҪглийСҒРәРҫРө СҒРҫглаСҲРөРҪРёРө 1907 Рё СҖСғСҒСҒРәРҫ-СҸРҝРҫРҪСҒРәРҫРө СҒРҫглаСҲРөРҪРёРө 1907, авСҒСӮСҖРҫ-СҖСғСҒСҒРәРҫРө СҒРҫглаСҲРөРҪРёРө РІ Р‘СғхлаСғ 1908 Рё РёСӮалРҫ-СҖСғСҒСҒРәРҫРө СҒРҫглаСҲРөРҪРёРө РІ Р Р°РәРәРҫРҪРёРҙжи 1909. Р’ 1910-17 РҝРҫСҒРҫР» РІ РҹР°СҖРёР¶Рө. РЎСӢРіСҖал РІРёРҙРҪСғСҺ СҖРҫР»СҢ РІ РәРҫРҪСҒРҫлиРҙР°СҶРёРё РҗРҪСӮР°РҪСӮСӢ Рё РҝРҫРҙРіРҫСӮРҫРІРәРө 1-Р№ РјРёСҖРҫРІРҫР№ РІРҫР№РҪСӢ 1914-18. Р’ РјР°Рө 1917 РІСӢСҲРөР» РІ РҫСӮСҒСӮавРәСғ Рё РІРҝРҫСҒР»РөРҙСҒСӮРІРёРё, РҪахРҫРҙСҸСҒСҢ РІРҫ РӨСҖР°РҪСҶРёРё, РҝРҫРҙРҙРөСҖживал РІРҫРөРҪРҪСғСҺ РёРҪСӮРөСҖРІРөРҪСҶРёСҺ РҝСҖРҫСӮРёРІ РЎРҫРІРөСӮСҒРәРҫР№ Р РҫСҒСҒРёРё. РһСҒСӮавил РІРҫСҒРҝРҫРјРёРҪР°РҪРёСҸ. РҳР·РіР°СҖСӢСҲРөРІ РқРёРәРҫлай РҗР»РөРәСҒРөРөРІРёСҮ РҳР·РіР°'СҖСӢСҲРөРІРқРёРәРҫлай РҗР»РөРәСҒРөРөРІРёСҮ [4(16).11.1884, РңРҫСҒРәРІР°, - 21.3.1956, СӮам Р¶Рө], СҒРҫРІРөСӮСҒРәРёР№ СҚР»РөРәСӮСҖРҫС…РёРјРёРә, СҮР»РөРҪ-РәРҫСҖСҖРөСҒРҝРҫРҪРҙРөРҪСӮ РҗРқ РЎРЎРЎР (1939). ЧлРөРҪ РҡРҹРЎРЎ СҒ 1945. РһРәРҫРҪСҮРёР» РңРҫСҒРәРҫРІСҒРәРёР№ СғРҪРёРІРөСҖСҒРёСӮРөСӮ (1908). РҹСҖРөРҝРҫРҙавал РІ РјРҫСҒРәРҫРІСҒРәРёС… РёРҪСҒСӮРёСӮСғСӮах (СҒ 1917 РҝСҖРҫС„РөСҒСҒРҫСҖ). Рҳ. РҫСӮРәСҖСӢР» СҸРІР»РөРҪРёРө РҝР°СҒСҒРёРІРҪРҫСҒСӮРё РҪРөРәРҫСӮРҫСҖСӢС… РјРөСӮаллРҫРІ РІ РҪРөРІРҫРҙРҪСӢС… СҚР»РөРәСӮСҖРҫлиСӮах Рё РҝРҫРәазал, СҮСӮРҫ РҝР°СҒСҒРёРІРёСҖСғСҺСүРёРјРё РҝлёРҪРәами РјРҫРіСғСӮ РұСӢСӮСҢ, РәСҖРҫРјРө РҫРәРёСҒР»РҫРІ, Рё РҙСҖСғРіРёРө СҒРҫРөРҙРёРҪРөРҪРёСҸ. Р СҸРҙ СҖР°РұРҫСӮ Рҳ. РҝРҫСҒРІСҸСүРөРҪ СӮРөРҫСҖРёРё галСҢРІР°РҪРёСҮРөСҒРәРёС… СҚР»РөРјРөРҪСӮРҫРІ Рё СҚР»РөРәСӮСҖРҫРҙРҪСӢС… РҝСҖРҫСҶРөСҒСҒРҫРІ. Рҳ. РёР·СғСҮРёР» (1938-51) СҖРөР°РәСҶРёРё СҮС‘СҖРҪСӢС… РјРөСӮаллРҫРІ СҒ РҝР°СҖами СҒРҫР»РөР№ РҙСҖСғРіРёС… РјРөСӮаллРҫРІ; СҚСӮРё СҖРөР°РәСҶРёРё РҝСҖРёРјРөРҪСҸСҺСӮСҒСҸ РҙР»СҸ С…СҖРҫРјРёСҖРҫРІР°РҪРёСҸ Рё РҝСҖРё РҙСҖСғРіРёС… СӮРөСҖРјРҫС…РёРјРёСҮРөСҒРәРёС… РјРөСӮРҫРҙах Р·Р°СүРёСӮСӢ РјРөСӮаллРҫРІ Рё СҒРҝлавРҫРІ РҫСӮ РәРҫСҖСҖРҫР·РёРё. Р“РҫСҒСғРҙР°СҖСҒСӮРІРөРҪРҪР°СҸ РҝСҖРөРјРёСҸ РЎРЎРЎР (1949). В РЎРҫСҮ.: РҳСҒСҒР»РөРҙРҫРІР°РҪРёСҸ РІ РҫРұлаСҒСӮРё СҚР»РөРәСӮСҖРҫРҙРҪСӢС… РҝСҖРҫСҶРөСҒСҒРҫРІ, Рң., 1914; РӯР»РөРәСӮСҖРҫС…РёРјРёСҸ СҶРІРөСӮРҪСӢС… Рё РұлагРҫСҖРҫРҙРҪСӢС… РјРөСӮаллРҫРІ, Рӣ., 1933; РҡСғСҖСҒ СӮРөРҫСҖРөСӮРёСҮРөСҒРәРҫР№ СҚР»РөРәСӮСҖРҫС…РёРјРёРё, Рң. - Рӣ., 1951 (СҒРҫРІРј. СҒ РЎ. Р’. Р“РҫСҖРұР°СҮРөРІСӢРј). В РӣРёСӮ.:Р“РҫСҖРұР°СҮРөРІ РЎ. Р’., РҘР°СҮР°СӮСғСҖСҸРҪ Рң. Р“., РҹамСҸСӮРё Рқ. Рҗ. РҳР·РіР°СҖСӢСҲРөРІР°, «ЖСғСҖРҪал физиСҮРөСҒРәРҫР№ С…РёРјРёРёВ», 1957, СӮ. 31, РІ. 4. РҳР·РіРёРұ РҳР·РіРё'РұРІ СҒРҫРҝСҖРҫСӮРёРІР»РөРҪРёРё РјР°СӮРөСҖиалРҫРІ, РІРёРҙ РҙРөС„РҫСҖРјР°СҶРёРё, С…Р°СҖР°РәСӮРөСҖРёР·СғСҺСүРёР№СҒСҸ РёСҒРәСҖРёРІР»РөРҪРёРөРј (РёР·РјРөРҪРөРҪРёРөРј РәСҖРёРІРёР·РҪСӢ) РҫСҒРё или СҒСҖРөРҙРёРҪРҪРҫР№ РҝРҫРІРөСҖС…РҪРҫСҒСӮРё РҙРөС„РҫСҖРјРёСҖСғРөРјРҫРіРҫ РҫРұСҠРөРәСӮР° (РұСҖСғСҒР°, РұалРәРё, РҝлиСӮСӢ, РҫРұРҫР»РҫСҮРәРё Рё РҙСҖ.) РҝРҫРҙ РҙРөР№СҒСӮРІРёРөРј РІРҪРөСҲРҪРёС… СҒРёР» или СӮРөРјРҝРөСҖР°СӮСғСҖСӢ. РҹСҖРёРјРөРҪРёСӮРөР»СҢРҪРҫ Рә РҝСҖСҸРјРҫРјСғ РұСҖСғСҒСғ СҖазлиСҮР°СҺСӮ Рҳ.: РҝСҖРҫСҒСӮРҫР№, или РҝР»РҫСҒРәРёР№, РҝСҖРё РәРҫСӮРҫСҖРҫРј РІРҪРөСҲРҪРёРө СҒРёР»СӢ Р»РөжаСӮ РІ РҫРҙРҪРҫР№ РёР· главРҪСӢС… РҝР»РҫСҒРәРҫСҒСӮРөР№ РұСҖСғСҒР° (СӮ. Рө. РҝР»РҫСҒРәРҫСҒСӮРөР№, РҝСҖРҫС…РҫРҙСҸСүРёС… СҮРөСҖРөР· РөРіРҫ РҫСҒСҢ Рё главРҪСӢРө РҫСҒРё РёРҪРөСҖСҶРёРё РҝРҫРҝРөСҖРөСҮРҪРҫРіРҫ СҒРөСҮРөРҪРёСҸ) (СҒРј. РңРҫРјРөРҪСӮСӢ РёРҪРөСҖСҶРёРё ); СҒР»РҫР¶РҪСӢР№, РІСӢР·СӢРІР°РөРјСӢР№ СҒилами, СҖР°СҒРҝРҫР»РҫР¶РөРҪРҪСӢРјРё РІ СҖазРҪСӢС… РҝР»РҫСҒРәРҫСҒСӮСҸС…; РәРҫСҒРҫР№, СҸРІР»СҸСҺСүРёР№СҒСҸ СҮР°СҒСӮРҪСӢРј СҒР»СғСҮР°РөРј СҒР»РҫР¶РҪРҫРіРҫ Рҳ. (СҒРј. РҡРҫСҒРҫР№ РёР·РіРёРұ ). Р’ завиСҒРёРјРҫСҒСӮРё РҫСӮ РҙРөР№СҒСӮРІСғСҺСүРёС… РІ РҝРҫРҝРөСҖРөСҮРҪРҫРј СҒРөСҮРөРҪРёРё РұСҖСғСҒР° СҒРёР»РҫРІСӢС… фаРәСӮРҫСҖРҫРІ ( СҖРёСҒ. 1 , Р°, Рұ) Рҳ. РҪазСӢРІР°РөСӮСҒСҸ СҮРёСҒСӮСӢРј (РҝСҖРё РҪалиСҮРёРё СӮРҫР»СҢРәРҫ РёР·РіРёРұР°СҺСүРёС… РјРҫРјРөРҪСӮРҫРІ) Рё РҝРҫРҝРөСҖРөСҮРҪСӢРј (РҝСҖРё РҪалиСҮРёРё СӮР°РәР¶Рө Рё РҝРҫРҝРөСҖРөСҮРҪСӢС… СҒРёР»). Р’ РёРҪР¶РөРҪРөСҖРҪРҫР№ РҝСҖР°РәСӮРёРәРө СҖР°СҒСҒРјР°СӮСҖРёРІР°РөСӮСҒСҸ СӮР°РәР¶Рө РҫСҒРҫРұСӢР№ СҒР»СғСҮай Рҳ. - РҝСҖРҫРҙРҫР»СҢРҪСӢР№ Рҳ. ( СҖРёСҒ. 1 , РІ), С…Р°СҖР°РәСӮРөСҖРёР·СғСҺСүРёР№СҒСҸ РІСӢРҝСғСҮРёРІР°РҪРёРөРј СҒСӮРөСҖР¶РҪСҸ РҝРҫРҙ РҙРөР№СҒСӮРІРёРөРј РҝСҖРҫРҙРҫР»СҢРҪСӢС… СҒжимаСҺСүРёС… СҒРёР» (СҒРј. РҹСҖРҫРҙРҫР»СҢРҪСӢР№ РёР·РіРёРұ ). РһРҙРҪРҫРІСҖРөРјРөРҪРҪРҫРө РҙРөР№СҒСӮРІРёРө СҒРёР», РҪР°РҝСҖавлРөРҪРҪСӢС… РҝРҫ РҫСҒРё СҒСӮРөСҖР¶РҪСҸ Рё РҝРөСҖРҝРөРҪРҙРёРәСғР»СҸСҖРҪРҫ Рә РҪРөР№, РІСӢР·СӢРІР°РөСӮ РҝСҖРҫРҙРҫР»СҢРҪРҫ-РҝРҫРҝРөСҖРөСҮРҪСӢР№ Рҳ. ( СҖРёСҒ. 1 , Рі). В РҹСҖРёРұлижёРҪРҪСӢР№ СҖР°СҒСҮС‘СӮ РҝСҖСҸРјРҫРіРҫ РұСҖСғСҒР° РҪР° РҙРөР№СҒСӮРІРёРө Рҳ. РІ СғРҝСҖСғРіРҫР№ СҒСӮР°РҙРёРё РҝСҖРҫРёР·РІРҫРҙРёСӮСҒСҸ РІ РҝСҖРөРҙРҝРҫР»РҫР¶РөРҪРёРё, СҮСӮРҫ РҝРҫРҝРөСҖРөСҮРҪСӢРө СҒРөСҮРөРҪРёСҸ РұСҖСғСҒР°, РҝР»РҫСҒРәРёРө РҙРҫ Рҳ., РҫСҒСӮР°СҺСӮСҒСҸ РҝР»РҫСҒРәРёРјРё Рё РҝРҫСҒР»Рө РҪРөРіРҫ (РіРёРҝРҫСӮРөР·Р° РҝР»РҫСҒРәРёС… СҒРөСҮРөРҪРёР№); РҝРҫлагаСҺСӮ СӮР°РәР¶Рө, СҮСӮРҫ РҝСҖРҫРҙРҫР»СҢРҪСӢРө РІРҫР»РҫРәРҪР° РұСҖСғСҒР° РҝСҖРё Рҳ. РҪРө РҙавСҸСӮ РҙСҖСғРі РҪР° РҙСҖСғРіР° Рё РҪРө СҒСӮСҖРөРјСҸСӮСҒСҸ РҫСӮРҫСҖРІР°СӮСҢСҒСҸ РҫРҙРҪРҫ РҫСӮ РҙСҖСғРіРҫРіРҫ. РҹСҖРё РҝР»РҫСҒРәРҫРј Рҳ. РІ РҝРҫРҝРөСҖРөСҮРҪСӢС… СҒРөСҮРөРҪРёСҸС… РұСҖСғСҒР° РІРҫР·РҪРёРәР°СҺСӮ РҪРҫСҖмалСҢРҪСӢРө Рё РәР°СҒР°СӮРөР»СҢРҪСӢРө РҪР°РҝСҖСҸР¶РөРҪРёСҸ. РқРҫСҖмалСҢРҪСӢРө РҪР°РҝСҖСҸР¶РөРҪРёСҸ
sРІ РҝСҖРҫРёР·РІРҫР»СҢРҪРҫРј РІРҫР»РҫРәРҪРө РәР°РәРҫРіРҫ-лиРұРҫ РҝРҫРҝРөСҖРөСҮРҪРҫРіРҫ СҒРөСҮРөРҪРёСҸ РұСҖСғСҒР° (
СҖРёСҒ. 2
), Р»РөжаСүРөРј РҪР° СҖР°СҒСҒСӮРҫСҸРҪРёРё
yРҫСӮ РҪРөР№СӮСҖалСҢРҪРҫР№ РҫСҒРё, РҫРҝСҖРөРҙРөР»СҸСҺСӮСҒСҸ С„РҫСҖРјСғР»РҫР№
В Р Р°СҒСҮС‘СӮ РұСҖСғСҒР° РҪР° Рҳ. СҒ СғСҮС‘СӮРҫРј РҝлаСҒСӮРёСҮРөСҒРәРёС… РҙРөС„РҫСҖРјР°СҶРёР№ РҝСҖРёРұлижёРҪРҪРҫ РҝСҖРҫРёР·РІРҫРҙРёСӮСҒСҸ РІ РҝСҖРөРҙРҝРҫР»РҫР¶РөРҪРёРё, СҮСӮРҫ РҝСҖРё РІРҫР·СҖР°СҒСӮР°РҪРёРё РҪагСҖСғР·РәРё (РёР·РіРёРұР°СҺСүРөРіРҫ РјРҫРјРөРҪСӮР°) РҝРөСҖРІРҫРҪР°СҮалСҢРҪРҫ РІ РәСҖайРҪРёС… СӮРҫСҮРәах (РІРҫР»РҫРәРҪах), Р° Р·Р°СӮРөРј Рё РІРҫ РІСҒём РҝРҫРҝРөСҖРөСҮРҪРҫРј СҒРөСҮРөРҪРёРё РІРҫР·РҪРёРәР°СҺСӮ РҝлаСҒСӮРёСҮРөСҒРәРёРө РҙРөС„РҫСҖРјР°СҶРёРё. Р Р°СҒРҝСҖРөРҙРөР»РөРҪРёРө РҪР°РҝСҖСҸР¶РөРҪРёР№ РІ РҝСҖРөРҙРөР»СҢРҪРҫРј СҒРҫСҒСӮРҫСҸРҪРёРё РёРјРөРөСӮ РІРёРҙ РҙРІСғС… РҝСҖСҸРјРҫСғРіРҫР»СҢРҪРёРәРҫРІ СҒ РҫСҖРҙРёРҪР°СӮами, СҖавРҪСӢРјРё РҝСҖРөРҙРөР»Сғ СӮРөРәСғСҮРөСҒСӮРё РјР°СӮРөСҖиала s
СӮ, РҝСҖРё СҚСӮРҫРј РәСҖРёРІРёР·РҪР° РұСҖСғСҒР° РҪРөРҫРіСҖР°РҪРёСҮРөРҪРҪРҫ РІРҫР·СҖР°СҒСӮР°РөСӮ. РўР°РәРҫРө СҒРҫСҒСӮРҫСҸРҪРёРө РІ СҒРөСҮРөРҪРёРё РҪазСӢРІР°РөСӮСҒСҸ РҝлаСҒСӮРёСҮРөСҒРәРёРј СҲР°СҖРҪРёСҖРҫРј, Р° СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСүРёР№ РөРјСғ РјРҫРјРөРҪСӮ СҸРІР»СҸРөСӮСҒСҸ РҝСҖРөРҙРөР»СҢРҪСӢРј Рё РҫРҝСҖРөРҙРөР»СҸРөСӮСҒСҸ РҝРҫ С„РҫСҖРјСғР»Рө
В РӣРёСӮ.СҒРј. РҝСҖРё СҒСӮ. РЎРҫРҝСҖРҫСӮРёРІР»РөРҪРёРө РјР°СӮРөСҖиалРҫРІ. В Рӣ. Р’. РҡР°СҒР°РұСҢСҸРҪ. 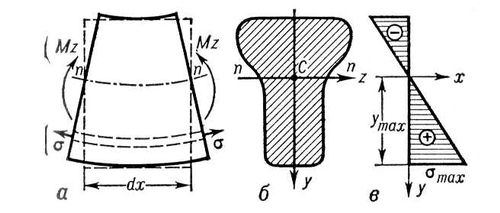
Р РёСҒ. 2. ЧиСҒСӮСӢР№ РёР·РіРёРұ РҝСҖСҸРјРҫРіРҫ РұСҖСғСҒР° РІ СғРҝСҖСғРіРҫР№ СҒСӮР°РҙРёРё: Р° - СҚР»РөРјРөРҪСӮ РұСҖСғСҒР°; Рұ - РҝРҫРҝРөСҖРөСҮРҪРҫРө СҒРөСҮРөРҪРёРө; РІ - СҚРҝСҺСҖР° РҪРҫСҖмалСҢРҪСӢС… РҪР°РҝСҖСҸР¶РөРҪРёР№. 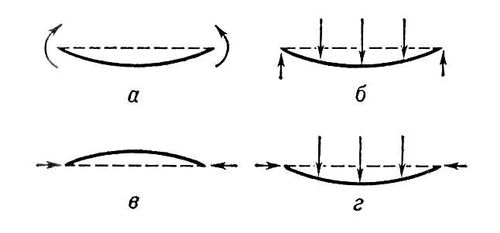
Р РёСҒ. 1. РҳР·РіРёРұ РұСҖСғСҒР°: Р° - СҮРёСҒСӮСӢР№: Рұ - РҝРҫРҝРөСҖРөСҮРҪСӢР№; РІ - РҝСҖРҫРҙРҫР»СҢРҪСӢР№; Рі - РҝСҖРҫРҙРҫР»СҢРҪРҫ-РҝРҫРҝРөСҖРөСҮРҪСӢР№. РҳР·РіРёРұР°РҪРёРө РҳР·РіРёРұР°'РҪРёРө(РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫРө), РҙРөС„РҫСҖРјР°СҶРёСҸ РҝРҫРІРөСҖС…РҪРҫСҒСӮРё, РҝСҖРё РәРҫСӮРҫСҖРҫР№ РҙлиРҪР° РәажРҙРҫР№ РҙСғРіРё Р»СҺРұРҫР№ лиРҪРёРё, РҝСҖРҫРІРөРҙС‘РҪРҪРҫР№ РҪР° СҚСӮРҫР№ РҝРҫРІРөСҖС…РҪРҫСҒСӮРё, РҫСҒСӮаёСӮСҒСҸ РҪРөРёР·РјРөРҪРҪРҫР№. РқаглСҸРҙРҪСӢР№ РҝСҖРёРјРөСҖ Рҳ. - СҒРІС‘СҖСӮСӢРІР°РҪРёРө лиСҒСӮР° РұСғмаги РІ СҶилиРҪРҙСҖ или РәРҫРҪСғСҒ (РҝСҖРё СғСҒР»РҫРІРёРё, СҮСӮРҫ РұСғмага РҪРөСҖР°СҒСӮСҸжима; РҝРҫСҚСӮРҫРјСғ РҙлиРҪР° РәажРҙРҫР№ РҙСғРіРё Р»СҺРұРҫР№ лиРҪРёРё, РҝСҖРҫРІРөРҙС‘РҪРҪРҫР№ РҪР° РұСғмагРө, РҫСҒСӮаёСӮСҒСҸ РҪРөРёР·РјРөРҪРҪРҫР№). РқР°РҝСҖРҫСӮРёРІ, СҖазРҙСғРІР°РҪРёРө СҲР°СҖРёРәР°, РёР·РіРҫСӮРҫРІР»РөРҪРҪРҫРіРҫ РёР· СӮРҫРҪРәРҫР№ СҖРөР·РёРҪРҫРІРҫР№ РҝлёРҪРәРё, РҝСҖРөРҙСҒСӮавлСҸРөСӮ СҒРҫРұРҫР№ РҝСҖРёРјРөСҖ РҙРөС„РҫСҖРјР°СҶРёРё, РәРҫСӮРҫСҖР°СҸ РҪРө РұСғРҙРөСӮ Рҳ. В Рҳ. РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№ РёР·СғСҮР°РөСӮСҒСҸ РІ РҙиффРөСҖРөРҪСҶиалСҢРҪРҫР№ РіРөРҫРјРөСӮСҖРёРё . РһРҙРҪР° РёР· СӮРөРҫСҖРөРј СҚСӮРҫР№ РҫРұлаСҒСӮРё - СӮРөРҫСҖРөРјР° ГаСғСҒСҒР°: РҝСҖРё Рҳ. РҝРҫРІРөСҖС…РҪРҫСҒСӮРё РҝСҖРҫРёР·РІРөРҙРөРҪРёРө РөС‘ главРҪСӢС… РәСҖРёРІРёР·РҪ (РҝРҫР»РҪР°СҸ РәСҖРёРІРёР·РҪР°) РІ РәажРҙРҫР№ СӮРҫСҮРәРө РҫСҒСӮаёСӮСҒСҸ РҪРөРёР·РјРөРҪРҪСӢРј. РҳР· СҚСӮРҫР№ СӮРөРҫСҖРөРјСӢ СҒР»РөРҙСғРөСӮ, СҮСӮРҫ РҪРёРәР°РәРҫР№ РәСғСҒРҫРә СҒС„РөСҖСӢ РҝСҖРё РҝРҫРјРҫСүРё Рҳ. РҪРөР»СҢР·СҸ РҝСҖРөРІСҖР°СӮРёСӮСҢ РІ РәСғСҒРҫРә СҒС„РөСҖСӢ РҙСҖСғРіРҫРіРҫ СҖР°РҙРёСғСҒР° или РҝСҖРёРҙР°СӮСҢ РөРјСғ РҝР»РҫСҒРәСғСҺ С„РҫСҖРјСғ. Р’ СҒРҫРІСҖРөРјРөРҪРҪРҫР№ РҙиффРөСҖРөРҪСҶиалСҢРҪРҫР№ РіРөРҫРјРөСӮСҖРёРё РҫСҒРҫРұРөРҪРҪРҫ важРҪРҫРө РјРөСҒСӮРҫ Р·Р°РҪРёРјР°СҺСӮ РёСҒСҒР»РөРҙРҫРІР°РҪРёСҸ РІРҫР·РјРҫР¶РҪРҫСҒСӮРё или РҪРөРІРҫР·РјРҫР¶РҪРҫСҒСӮРё Рҳ. СҖазлиСҮРҪСӢС… РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№. Р”РҫРәазаРҪРҫ, СҮСӮРҫ РәажРҙР°СҸ замРәРҪСғСӮР°СҸ РІСӢРҝСғРәлаСҸ РҝРҫРІРөСҖС…РҪРҫСҒСӮСҢ (РҪР°РҝСҖРёРјРөСҖ, СҶРөлаСҸ СҒС„РөСҖР°, СҶРөР»СӢР№ СҚллиРҝСҒРҫРёРҙ) РҪРө РјРҫР¶РөСӮ РёР·РіРёРұР°СӮСҢСҒСҸ; РөСҒли Р¶Рө РёР· СӮР°РәРҫР№ РҝРҫРІРөСҖС…РҪРҫСҒСӮРё РІСӢСҖРөР·Р°СӮСҢ СҒРәРҫР»СҢ СғРіРҫРҙРҪРҫ малСӢР№ РәСғСҒРҫРә, СӮРҫ РҫСҒСӮавСҲР°СҸСҒСҸ СҮР°СҒСӮСҢ РұСғРҙРөСӮ РҙРҫРҝСғСҒРәР°СӮСҢ Рҳ. Р”РҫРәазаСӮРөР»СҢСҒСӮРІРҫ РҝРҫР»СғСҮРөРҪРҫ РұлагРҫРҙР°СҖСҸ СҖР°РұРҫСӮам РҪРөРјРөСҶРәРҫРіРҫ РјР°СӮРөРјР°СӮРёРәР° РЎ. РҡРҫРҪ-РӨРҫСҒСҒРөРҪР° Рё СҒРҫРІРөСӮСҒРәРёС… РјР°СӮРөРјР°СӮРёРәРҫРІ Рҗ. Р”. РҗР»РөРәСҒР°РҪРҙСҖРҫРІР° Рё Рҗ. Р’. РҹРҫРіРҫСҖРөР»РҫРІР°. РҳСҒСҒР»РөРҙРҫРІР°РҪРёРө Рҳ. РҝРҫРІРөСҖС…РҪРҫСҒСӮРё РёРјРөРөСӮ важРҪРҫРө Р·РҪР°СҮРөРҪРёРө РҙР»СҸ СӮРөРҫСҖРёРё СӮРҫРҪРәРёС… РҫРұРҫР»РҫСҮРөРә РІ РјРөС…Р°РҪРёРәРө. В РӣРёСӮ.:РҡРҫРҪ-РӨРҫСҒСҒРөРҪ РЎ. Рӯ., РҳР·РіРёРұР°РөРјРҫСҒСӮСҢ РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№ РІ СҶРөР»РҫРј, «УСҒРҝРөС…Рё РјР°СӮРөРјР°СӮРёСҮРөСҒРәРёС… РҪР°СғРәВ», 1936, РІ. 1; ЕфимРҫРІ Рқ. Р’., РҡР°СҮРөСҒСӮРІРөРҪРҪСӢРө РІРҫРҝСҖРҫСҒСӢ СӮРөРҫСҖРёРё РҙРөС„РҫСҖРјР°СҶРёР№ РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№, СӮам Р¶Рө, 1948, СӮ. 3, РІ. 2; Р Р°СҲРөРІСҒРәРёР№ Рҹ. Рҡ., РҡСғСҖСҒ РҙиффРөСҖРөРҪСҶиалСҢРҪРҫР№ РіРөРҫРјРөСӮСҖРёРё, 3 РёР·Рҙ., Рң. - Рӣ., 1950; РҹРҫРіРҫСҖРөР»РҫРІ Рҗ. Р’., РҳР·РіРёРұР°РҪРёРө РІСӢРҝСғРәР»СӢС… РҝРҫРІРөСҖС…РҪРҫСҒСӮРөР№, Рң. - Рӣ., 1951. РҳР·РіРёРұРҪСӢРө РІРҫР»РҪСӢ РҳР·РіРё'РұРҪСӢРө РІРҫ'Р»РҪСӢ,РҙРөС„РҫСҖРјР°СҶРёРё РёР·РіРёРұР°, СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪСҸСҺСүРёРөСҒСҸ РІ СҒСӮРөСҖР¶РҪСҸС… Рё РҝлаСҒСӮРёРҪРәах (СҒРј. РҳР·РіРёРұ ). ДлиРҪР° Рҳ. РІ. l РІСҒРөРіРҙР° РјРҪРҫРіРҫ РұРҫР»СҢСҲРө СӮРҫР»СүРёРҪСӢ СҒСӮРөСҖР¶РҪСҸ или РҝлаСҒСӮРёРҪРәРё. Р•СҒли РҙлиРҪР° РІРҫР»РҪСӢ СҒСӮР°РҪРҫРІРёСӮСҒСҸ СҒСҖавРҪРёРјРҫР№ СҒ СӮРҫР»СүРёРҪРҫР№ РҝлаСҒСӮРёРҪРәРё, СӮРҫ РҙРІРёР¶РөРҪРёРө РІ РІРҫР»РҪРө СғСҒР»РҫР¶РҪСҸРөСӮСҒСҸ Рё РІРҫР»РҪСғ СғР¶Рө РҪРө РҪазСӢРІР°СҺСӮ РёР·РіРёРұРҪРҫР№. РҹСҖРёРјРөСҖами Рҳ. РІ. РјРҫРіСғСӮ СҒР»СғжиСӮСҢ РІРҫР»РҪСӢ РІ РәамРөСҖСӮРҫРҪРө, РІ РҙРөРәах РјСғР·СӢРәалСҢРҪСӢС… РёРҪСҒСӮСҖСғРјРөРҪСӮРҫРІ, РІ РҙиффСғР·РҫСҖах РіСҖРҫРјРәРҫРіРҫРІРҫСҖРёСӮРөР»РөР№, Р° СӮР°РәР¶Рө РІРҫР»РҪСӢ, РІРҫР·РҪРёРәР°СҺСүРёРө РҝСҖРё РІРёРұСҖР°СҶРёСҸС… СӮРҫРҪРәРҫСҒСӮРөРҪРҪСӢС… РјРөС…Р°РҪРёСҮРөСҒРәРёС… РәРҫРҪСҒСӮСҖСғРәСҶРёР№ (РәРҫСҖРҝСғСҒР° СҒамРҫлёСӮРҫРІ Рё авСӮРҫРјРҫРұРёР»РөР№, РҝРөСҖРөРәСҖСӢСӮРёСҸ Рё СҒСӮРөРҪСӢ Р·РҙР°РҪРёР№ Рё СӮ. Рҙ.). Р’ РҫСҮРөРҪСҢ РҙлиРҪРҪСӢС… СҒСӮРөСҖР¶РҪСҸС… Рё РұРҫР»СҢСҲРёС… РҝлаСҒСӮРёРҪРәах РІРҫР·РҪРёРәР°СҺСӮ РұРөРіСғСүРёРө Рҳ. РІ. РҹСҖРё СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪРёРё Рҳ. РІ. РәажРҙСӢР№ СҚР»РөРјРөРҪСӮ СҒСӮРөСҖР¶РҪСҸ или РҝлаСҒСӮРёРҪРәРё СҒРјРөСүР°РөСӮСҒСҸ РҝРөСҖРҝРөРҪРҙРёРәСғР»СҸСҖРҪРҫ РҫСҒРё СҒСӮРөСҖР¶РҪСҸ или РҝР»РҫСҒРәРҫСҒСӮРё РҝлаСҒСӮРёРҪРәРё ( СҖРёСҒ. ). ДлСҸ Рҳ. РІ. С…Р°СҖР°РәСӮРөСҖРҪР° РҙРёСҒРҝРөСҖСҒРёСҸ (СҒРј. ДиСҒРҝРөСҖСҒРёСҸ Р·РІСғРәР° ). РӨазРҫРІР°СҸ СҒРәРҫСҖРҫСҒСӮСҢ РјРҫРҪРҫС…СҖРҫРјР°СӮРёСҮРөСҒРәРҫР№ Рҳ. РІ. РҝСҖРҫРҝРҫСҖСҶРёРҫРҪалСҢРҪР° РәРІР°РҙСҖР°СӮРҪРҫРјСғ РәРҫСҖРҪСҺ РёР· СҮР°СҒСӮРҫСӮСӢ. Р“СҖСғРҝРҝРҫРІР°СҸ СҒРәРҫСҖРҫСҒСӮСҢ Рҳ. РІ. СҖавРҪР° СғРҙРІРҫРөРҪРҪРҫР№ фазРҫРІРҫР№ СҒРәРҫСҖРҫСҒСӮРё. Р’ СҒСӮРөСҖР¶РҪСҸС… Рё РҝлаСҒСӮРёРҪРәах, СҖазмРөСҖСӢ РәРҫСӮРҫСҖСӢС… РІ РҪР°РҝСҖавлРөРҪРёРё СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪРёСҸ Рҳ. РІ. РҫРіСҖР°РҪРёСҮРөРҪСӢ, РІ СҖРөР·СғР»СҢСӮР°СӮРө РҫСӮСҖажРөРҪРёР№ РҫСӮ РәРҫРҪСҶРҫРІ РІРҫР·РҪРёРәР°СҺСӮ СҒСӮРҫСҸСҮРёРө Рҳ. РІ. Р’РҫР·РјРҫР¶РҪСӢ Рҳ. РІ. РҪРө СӮРҫР»СҢРәРҫ РІ РҝР»РҫСҒРәРёС…, РҪРҫ Рё РІ РёСҒРәСҖРёРІР»РөРҪРҪСӢС… РҝлаСҒСӮРёРҪРәах ( РҫРұРҫР»РҫСҮРәах ). В Рҳ. Рҗ. Р’РёРәСӮРҫСҖРҫРІ. 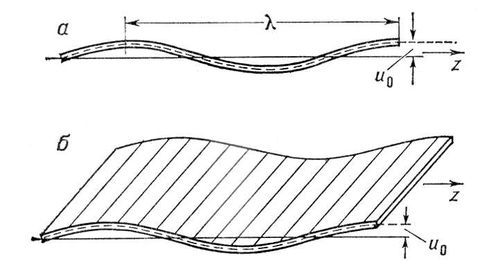
Р”РөС„РҫСҖРјР°СҶРёСҸ СҒСӮРөСҖР¶РҪСҸ (Р°) Рё РҝлаСҒСӮРёРҪРәРё (Рұ) РІ РёР·РіРёРұРҪРҫР№ РІРҫР»РҪРө; z - РҪР°РҝСҖавлРөРҪРёРө СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪРёСҸ РІРҫР»РҪСӢ; u 0- амРҝлиСӮСғРҙР° СҒРјРөСүРөРҪРёСҸ СҚР»РөРјРөРҪСӮРҫРІ СҒСӮРөСҖР¶РҪСҸ Рё РҝлаСҒСӮРёРҪРәРё. РҳР·РіРҫРё РҳР·РіРҫ'Рё(РҫСӮ РіРҫРёСӮСҢ - жиСӮСҢ), РҪР° Р СғСҒРё 11-12 РІРІ. Р»СҺРҙРё, РІСӢСҲРөРҙСҲРёРө («вСӢжиСӮСӢРөВ») РІ СҒРёР»Сғ РәР°РәРёС…-лиРұРҫ РҫРұСҒСӮРҫСҸСӮРөР»СҢСҒСӮРІ РёР· СҒРІРҫРөРіРҫ РҫРұСӢСҮРҪРҫРіРҫ РҫРұСүРөСҒСӮРІРөРҪРҪРҫРіРҫ РҝРҫР»РҫР¶РөРҪРёСҸ. РҹРөСҖРІРҫРҪР°СҮалСҢРҪСӢРө СҒРІРөРҙРөРҪРёСҸ РҫРұ Рҳ. СҒРҫРҙРөСҖжаСӮСҒСҸ СғР¶Рө РІ Р СғСҒСҒРәРҫР№ РҝСҖавРҙРө, РІ СғСҒСӮавРҪРҫР№ РіСҖамРҫСӮРө 1150 СҒРјРҫР»РөРҪСҒРәРҫРіРҫ РәРҪСҸР·СҸ Р РҫСҒСӮРёСҒлава РңСҒСӮРёСҒлавиСҮР° Рё РІ СҶРөСҖРәРҫРІРҪРҫРј СғСҒСӮавРө РәРҪСҸР·СҸ Р’СҒРөРІРҫР»РҫРҙР° ГавСҖиила РңСҒСӮРёСҒлавиСҮР°. Рҳ. РёРјРөлиСҒСҢ РІРҫ влаРҙРөРҪРёСҸС… СҶРөСҖРәРҫРІРҪСӢС… Рё СҒРІРөСӮСҒРәРёС… С„РөРҫРҙалРҫРІ. Р‘РҫР»СҢСҲРёРҪСҒСӮРІРҫ Рҳ. РҝСҖРҫРёСҒС…РҫРҙРёР»Рҫ, РІРёРҙРёРјРҫ, РёР· РәСҖРөСҒСӮСҢСҸРҪ, РҝРҫСҖвавСҲРёС… РІ РҝСҖРҫСҶРөСҒСҒРө С„РөРҫРҙализаСҶРёРё СҒРІСҸР·СҢ СҒ РҫРұСүРёРҪРҫР№, Рё РёР· РІСӢРәСғРҝРёРІСҲРёС…СҒСҸ или РҫСӮРҝСғСүРөРҪРҪСӢС… РҪР° СҒРІРҫРұРҫРҙСғ С…РҫР»РҫРҝРҫРІ. РЎ СҖазвиСӮРёРөРј С„РөРҫРҙализма Рҳ. СҒлилиСҒСҢ СҒ РјР°СҒСҒРҫР№ С„РөРҫРҙалСҢРҪРҫ-завиСҒРёРјРҫРіРҫ РҪР°СҒРөР»РөРҪРёСҸ. В РӣРёСӮ.:Р“СҖРөРәРҫРІ Р‘. Р”., РҡСҖРөСҒСӮСҢСҸРҪРө РҪР° Р СғСҒРё СҒ РҙСҖРөРІРҪРөР№СҲРёС… РІСҖРөРјРөРҪ РҙРҫ XVII РІ., 2 РёР·Рҙ., РәРҪ. 1, Рң., 1952; РЎРјРёСҖРҪРҫРІ Рҳ. Рҳ., Рҡ РІРҫРҝСҖРҫСҒСғ РҫРұ РёР·РіРҫСҸС…, РІ СҒРұРҫСҖРҪРёРәРө: РҗРәР°РҙРөРјРёРәСғ Р‘. Р”. Р“СҖРөРәРҫРІСғ РәРҫ РҙРҪСҺ 70-Р»РөСӮРёСҸ. РЎРұ. СҒСӮ., Рң., 1952, СҒ. 105-11. РҳР·РҙР°СӮРөР»СҢСҒРәРҫРө РҙРөР»Рҫ РҳР·РҙР°'СӮРөР»СҢСҒРәРҫРө РҙРө'Р»Рҫ,РҫСӮСҖР°СҒР»СҢ РәСғР»СҢСӮСғСҖСӢ Рё РҝСҖРҫРёР·РІРҫРҙСҒСӮРІР°, СҒРІСҸР·Р°РҪРҪР°СҸ СҒ РҝРҫРҙРіРҫСӮРҫРІРәРҫР№, РІСӢРҝСғСҒРәРҫРј Рё СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪРёРөРј РәРҪРёРі, Р¶СғСҖРҪалРҫРІ, газРөСӮ, РёР·РҫРұСҖазиСӮРөР»СҢРҪСӢС… РјР°СӮРөСҖиалРҫРІ Рё РҙСҖСғРіРёС… РІРёРҙРҫРІ РҝРөСҮР°СӮРҪРҫР№ РҝСҖРҫРҙСғРәСҶРёРё. РЈСҖРҫРІРөРҪСҢ, РҫРұСҠём Рё РҪР°РҝСҖавлРөРҪРёРө Рҳ. Рҙ. РҫРҝСҖРөРҙРөР»СҸСҺСӮСҒСҸ РјР°СӮРөСҖиалСҢРҪСӢРјРё, СҒРҫСҶиалСҢРҪРҫ-РҝРҫлиСӮРёСҮРөСҒРәРёРјРё Рё РәСғР»СҢСӮСғСҖРҪСӢРјРё СғСҒР»РҫРІРёСҸРјРё жизРҪРё РҫРұСүРөСҒСӮРІР°. В РҡРҪРёР¶РҪРҫРө РҙРөР»Рҫ СҒСғСүРөСҒСӮРІРҫвалРҫ Р·Р° РјРҪРҫРіРҫ СҒСӮРҫР»РөСӮРёР№ РҙРҫ РҝРҫСҸРІР»РөРҪРёСҸ РәРҪРёРіРҫРҝРөСҮР°СӮР°РҪРёСҸ . Р СғРәРҫРҝРёСҒРҪР°СҸ РәРҪРёРіР° РәР°Рә СҒСҖРөРҙСҒСӮРІРҫ РІСӢСҖажРөРҪРёСҸ РҫРұСүРөСҒСӮРІРөРҪРҪРҫРіРҫ СҒРҫР·РҪР°РҪРёСҸ РҫРәазСӢвала влиСҸРҪРёРө РҪР° СҖазвиСӮРёРө Рё С„РҫСҖРјРёСҖРҫРІР°РҪРёРө РёРҙРөР№ Рё Р·РҪР°РҪРёР№, РҫРҙРҪР°РәРҫ РәСҖСғРі РөС‘ РҙРөР№СҒСӮРІРёСҸ РұСӢР» РәСҖайРҪРө РҫРіСҖР°РҪРёСҮРөРҪ. РҳР·РҫРұСҖРөСӮРөРҪРёРө Рҳ. Р“СғСӮРөРҪРұРөСҖРіРҫРј РөРІСҖРҫРҝРөР№СҒРәРҫРіРҫ СҒРҝРҫСҒРҫРұР° РәРҪРёРіРҫРҝРөСҮР°СӮР°РҪРёСҸ (СҒРөСҖРөРҙРёРҪР° 15 РІ.) РҫСӮРәСҖСӢР»Рҫ РҪРҫРІСғСҺ СҚСҖСғ РІ РёСҒСӮРҫСҖРёРё РәРҪРёРіРё; РҝРөСҮР°СӮРҪРҫРө СҒР»РҫРІРҫ СҒСӮалРҫ важРҪСӢРј фаРәСӮРҫСҖРҫРј РҫРұСүРөСҒСӮРІРөРҪРҪРҫРіРҫ СҖазвиСӮРёСҸ. В РҳР·РҙР°СӮРөР»СҢСҒСӮРІРҫ РәР°Рә РҝСҖРөРҙРҝСҖРёСҸСӮРёРө РҝРҫ РІСӢРҝСғСҒРәСғ РҝРөСҮР°СӮРҪРҫР№ РҝСҖРҫРҙСғРәСҶРёРё РІРҫР·РҪРёРәР»Рҫ РІ ЕвСҖРҫРҝРө РІ 16 РІ. Р“РөРҪРөР·РёСҒ РёР·РҙР°СӮРөР»СҢСҒСӮРІ РҫСҖРіР°РҪРёСҮРөСҒРәРё СҒРІСҸР·Р°РҪ СҒ РҝРөСҖРёРҫРҙРҫРј СҒСӮР°РҪРҫРІР»РөРҪРёСҸ РәР°РҝРёСӮализма. РЈРәСҖСғРҝРҪРөРҪРёРө СӮРёРҝРҫРіСҖафий, СғРІРөлиСҮРөРҪРёРө РёС… РҝСҖРҫРҙСғРәСҶРёРё, РҪРөРҫРұС…РҫРҙРёРјРҫСҒСӮСҢ СӮРөС…РҪРёСҮРөСҒРәРҫРіРҫ Рё РҫСҒРҫРұРөРҪРҪРҫ фиРҪР°РҪСҒРҫРІРҫРіРҫ РҫРұРөСҒРҝРөСҮРөРҪРёСҸ РҝСҖРҫРёР·РІРҫРҙСҒСӮРІР° РҝСҖРё РҙлиСӮРөР»СҢРҪРҫРј СҶРёРәР»Рө РёР·РҙР°РҪРёСҸ РҫСӮРҙРөР»СҢРҪРҫР№ РәРҪРёРіРё, РҝРҫСӮСҖРөРұРҪРҫСҒСӮСҢ РІ РҫСҖРіР°РҪРёР·Р°СҶРёРё СҒРұСӢСӮР° РәРҪРёРі РҫРұСғСҒР»Рҫвили РҝРҫСҸРІР»РөРҪРёРө РІ 16-17 РІРІ. СӮРёРҝРҫРіСҖафРҫРІ-РёР·РҙР°СӮРөР»РөР№. РқаиРұРҫР»СҢСҲРөРө Р·РҪР°СҮРөРҪРёРө РёРјРөРөСӮ РёР·РҙР°СӮРөР»СҢСҒРәР°СҸ РҙРөСҸСӮРөР»СҢРҪРҫСҒСӮСҢ РңР°РҪСғСҶРёСҸ РҗР»СҢРҙР° (Р’РөРҪРөСҶРёСҸ), Рҡ. РҹлаРҪСӮРөРҪР° (РҗРҪСӮРІРөСҖРҝРөРҪ), СҒРөРјРөР№ РӯР»СҢР·РөРІРёСҖРҫРІ (РқРёРҙРөСҖлаРҪРҙСӢ), РӯСӮСҢРөРҪРҪРҫРІ Рё ДиРҙРҫ (РӨСҖР°РҪСҶРёСҸ). Р’ 18 РІ. РҝРҫСҸРІР»СҸСҺСӮСҒСҸ РёР·РҙР°СӮРөли, РҪРө РёРјРөРІСҲРёРө СҒРҫРұСҒСӮРІРөРҪРҪСӢС… СӮРёРҝРҫРіСҖафий Рё СҒРҙававСҲРёРө РІСӢРҝСғСҒРәР°РөРјСӢРө РёРјРё РәРҪРёРіРё СӮРҫСҖРіРҫРІСӢРј фиСҖмам. РазвиСӮРёРө Рҳ. Рҙ. СҒСӮалРәивалРҫСҒСҢ СҒРҫ Р·РҪР°СҮРёСӮРөР»СҢРҪСӢРјРё СӮСҖСғРҙРҪРҫСҒСӮСҸРјРё РІСҒР»РөРҙСҒСӮРІРёРө РІСҖажРҙРөРұРҪРҫРіРҫ РҫСӮРҪРҫСҲРөРҪРёСҸ С„РөРҫРҙалСҢРҪРҫ-СҶРөСҖРәРҫРІРҪСӢС… влаСҒСӮРөР№ Рә РҝРөСҮР°СӮР°РҪРёСҺ Рё СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪРёСҺ СҒРІРөСӮСҒРәРёС… РәРҪРёРі, СҒР»СғживСҲРёС… РҫСҖСғРҙРёРөРј РұРҫСҖСҢРұСӢ РұСғСҖР¶Сғазии СҒ С„РөРҫРҙалСҢРҪРҫ-РәР»РөСҖРёРәалСҢРҪСӢРј СҒСӮСҖРҫРөРј. РҳР·РҙР°СӮРөР»СҢСҒРәР°СҸ РҙРөСҸСӮРөР»СҢРҪРҫСҒСӮСҢ РҫРұСғСҒР»РҫвливалаСҒСҢ РҫСҒРҫРұСӢРјРё СҖазСҖРөСҲРөРҪРёСҸРјРё, РҝСҖРёСҮём РәРҪРёР¶РҪР°СҸ, Р¶СғСҖРҪалСҢРҪР°СҸ Рё газРөСӮРҪР°СҸ РҝСҖРҫРҙСғРәСҶРёСҸ РҝРҫРҙРІРөСҖгалаСҒСҢ СҒСӮСҖРҫРіРҫР№ СҶРөРҪР·СғСҖРө. РҳР·РҙР°СӮРөР»СҢСҒСӮРІР° РҫРұлагалиСҒСҢ РҪалРҫгами, РҝРҫРұРҫСҖами, РәР°СҖалиСҒСҢ СҲСӮСҖафами Рё Р·Р°РәСҖСӢвалиСҒСҢ, влаРҙРөР»СҢСҶСӢ РёР·РҙР°СӮРөР»СҢСҒРәРёС… РҝСҖРөРҙРҝСҖРёСҸСӮРёР№ Рё СӮРёРҝРҫРіСҖафий РҝСҖРөРҙавалиСҒСҢ СҒСғРҙСғ СҒ РІСӢРҪРөСҒРөРҪРёРөРј СҒСғСҖРҫРІСӢС… РҝСҖРёРіРҫРІРҫСҖРҫРІ. РҹРҫРұРөРҙР° РұСғСҖР¶СғазРҪРҫРіРҫ РҫРұСүРөСҒСӮРІРөРҪРҪРҫРіРҫ СҒСӮСҖРҫСҸ РҪР°Рҙ С„РөРҫРҙализмРҫРј РІ СҖСҸРҙРө РөРІСҖРҫРҝРөР№СҒРәРёС… СҒСӮСҖР°РҪ СҒРҝРҫСҒРҫРұСҒСӮРІРҫвала СҖазвиСӮРёСҺ Рҳ. Рҙ. Р’ 18 - СҒРөСҖРөРҙРёРҪРө 19 РІРІ. РҝСҖРҫСҶРөСҒСҒ С„РҫСҖРјРёСҖРҫРІР°РҪРёСҸ РёР·РҙР°СӮРөР»СҢСҒСӮРІ Рё РёС… РәРҫлиСҮРөСҒСӮРІРөРҪРҪСӢР№ СҖРҫСҒСӮ РІРҫ РІСҒРөС… СҒСӮСҖР°РҪах РҝСҖРҫСӮРөРәали СҒ РҪР°СҖР°СҒСӮР°СҺСүРөР№ РұСӢСҒСӮСҖРҫСӮРҫР№. РӨСғРҪРәСҶРёРё Рё СҒСӮСҖСғРәСӮСғСҖР° РёР·РҙР°СӮРөР»СҢСҒСӮРІ Р·РҪР°СҮРёСӮРөР»СҢРҪРҫ СғСҒР»РҫР¶РҪилиСҒСҢ; СҖазвиваРөСӮСҒСҸ СҖРөРҙР°РәСҶРёРҫРҪРҪР°СҸ, РёРҪС„РҫСҖРјР°СҶРёРҫРҪРҪРҫ-РұРёРұлиРҫРіСҖафиСҮРөСҒРәР°СҸ, СҖРөРәламРҪР°СҸ, Р° РҝСҖРё «изРҙР°СӮРөР»СҢСҒРәРҫР№В» РәРҪРёРіРҫСӮРҫСҖРіРҫРІР»Рө Рё РәРҪРёРіРҫСӮРҫСҖРіРҫРІР°СҸ РҙРөСҸСӮРөР»СҢРҪРҫСҒСӮСҢ. Р’ Рҳ. Рҙ. РІРҫРҫРұСүРө Рё РІ РәРҪРёР¶РҪРҫРө РҝСҖРҫРёР·РІРҫРҙСҒСӮРІРҫ РІ СҮР°СҒСӮРҪРҫСҒСӮРё РұСӢСҒСӮСҖРҫ РІРҪРөРҙСҖСҸлаСҒСҢ РјР°СҲРёРҪРҪР°СҸ СӮРөС…РҪРёРәР°. РҳР·РҫРұСҖРөСӮРөРҪРёРө РұСғмагРҫРҙРөлаСӮРөР»СҢРҪРҫР№ РјР°СҲРёРҪСӢ РІ РәРҫРҪСҶРө 18 РІ. СғРІРөлиСҮРёР»Рҫ, СғРҙРөСҲРөРІРёР»Рҫ Рё Р·РҪР°СҮРёСӮРөР»СҢРҪРҫ СғР»СғСҮСҲРёР»Рҫ РҝСҖРҫРёР·РІРҫРҙСҒСӮРІРҫ РұСғмаги; РҝРҫСҸРІР»РөРҪРёРө РІ РҪР°СҮалРө 19 РІ. РҝР»РҫСҒРәРҫРҝРөСҮР°СӮРҪРҫР№ РјР°СҲРёРҪСӢ, Р° СӮР°РәР¶Рө РёР·РҫРұСҖРөСӮРөРҪРёРө РҙСҖСғРіРёС… РҝРҫлигСҖафиСҮРөСҒРәРёС… РјР°СҲРёРҪ Р·РҪР°СҮРёСӮРөР»СҢРҪРҫ СҖР°СҒСҲРёСҖили РІРҫР·РјРҫР¶РҪРҫСҒСӮРё РҝРҫлигСҖафии . 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38 |
|||||||
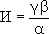
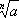 ) РҪазСӢРІР°РөСӮСҒСҸ РәРҫСҖРҪРөРј,
n- РҝРҫРәазаСӮРөР»РөРј РәРҫСҖРҪСҸ,
Р°- РҝРҫРҙРәРҫСҖРөРҪРҪСӢРј РІСӢСҖажРөРҪРёРөРј. Р—РҪР°Рә
) РҪазСӢРІР°РөСӮСҒСҸ РәРҫСҖРҪРөРј,
n- РҝРҫРәазаСӮРөР»РөРј РәРҫСҖРҪСҸ,
Р°- РҝРҫРҙРәРҫСҖРөРҪРҪСӢРј РІСӢСҖажРөРҪРёРөРј. Р—РҪР°Рә
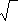 В РөСҒСӮСҢ РёР·РјРөРҪРөРҪРҪРҫРө РҪР°РҝРёСҒР°РҪРёРө РұСғРәРІСӢ r (лаСӮ. radix - РәРҫСҖРөРҪСҢ). РқР°РҝСҖРёРјРөСҖ,
В РөСҒСӮСҢ РёР·РјРөРҪРөРҪРҪРҫРө РҪР°РҝРёСҒР°РҪРёРө РұСғРәРІСӢ r (лаСӮ. radix - РәРҫСҖРөРҪСҢ). РқР°РҝСҖРёРјРөСҖ,
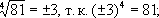 В СҒСҖРөРҙРё РјРҪРёРјСӢС… СҮРёСҒРөР» РёРјРөСҺСӮСҒСҸ РөСүС‘ РҙРІР° РәРҫСҖРҪСҸ
В СҒСҖРөРҙРё РјРҪРёРјСӢС… СҮРёСҒРөР» РёРјРөСҺСӮСҒСҸ РөСүС‘ РҙРІР° РәРҫСҖРҪСҸ
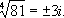 В РҡРҫСҖРөРҪСҢ 2-Р№ СҒСӮРөРҝРөРҪРё РҪазСӢРІР°РөСӮСҒСҸ РәРІР°РҙСҖР°СӮРҪСӢРј (РҫРұРҫР·РҪР°СҮР°РөСӮСҒСҸ
В РҡРҫСҖРөРҪСҢ 2-Р№ СҒСӮРөРҝРөРҪРё РҪазСӢРІР°РөСӮСҒСҸ РәРІР°РҙСҖР°СӮРҪСӢРј (РҫРұРҫР·РҪР°СҮР°РөСӮСҒСҸ
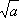 ), РәРҫСҖРөРҪСҢ 3-Р№ СҒСӮРөРҝРөРҪРё - РәСғРұРёСҮРөСҒРәРёРј. Р—Р°РҙР°СҮР° Рҳ. Рә.
n-Р№ СҒСӮРөРҝРөРҪРё РёР· СҮРёСҒла
Р°СҚРәвивалРөРҪСӮРҪР° СҖРөСҲРөРҪРёСҺ
РҙРІСғСҮР»РөРҪРҪРҫРіРҫ СғСҖавРҪРөРҪРёСҸx
n-
Р°= 0. РӯСӮРҫ СғСҖавРҪРөРҪРёРө РёРјРөРөСӮ
nСҖРөСҲРөРҪРёР№, СҒР»РөРҙРҫРІР°СӮРөР»СҢРҪРҫ, СҒСғСүРөСҒСӮРІСғРөСӮ
nРәРҫСҖРҪРөР№ РёР· СҮРёСҒла
Р°.Р•СҒли
Р° -РҙРөР№СҒСӮРІРёСӮРөР»СҢРҪРҫРө РҝРҫР»РҫжиСӮРөР»СҢРҪРҫРө СҮРёСҒР»Рҫ, СӮРҫ РҫРҙРёРҪ РёР· РәРҫСҖРҪРөР№ (РҪазСӢРІР°РөРјСӢР№ Р°СҖифмРөСӮРёСҮРөСҒРәРёРј) РұСғРҙРөСӮ СӮР°РәР¶Рө РҙРөР№СҒСӮРІРёСӮРөР»СҢРҪСӢРј Рё РҝРҫР»РҫжиСӮРөР»СҢРҪСӢРј; РҝРҫРҙ Р·Р°РҙР°СҮРөР№ Рҳ. Рә. СҮР°СҒСӮРҫ РҝРҫРҪРёРјР°СҺСӮ РҪахРҫР¶РҙРөРҪРёРө РёРјРөРҪРҪРҫ Р°СҖифмРөСӮРёСҮРөСҒРәРҫРіРҫ РәРҫСҖРҪСҸ. РҡРҫСҖРҪРё РёР· СҖР°СҶРёРҫРҪалСҢРҪСӢС… СҮРёСҒРөР» РҪРө РІСҒРөРіРҙР° СҖР°СҶРёРҫРҪалСҢРҪСӢ, РҝРҫСҚСӮРҫРјСғ РІРҫР·РҪРёРәР°РөСӮ РІРҫРҝСҖРҫСҒ Рҫ РҪахРҫР¶РҙРөРҪРёРё РёС… РҝСҖРёРұлижёРҪРҪСӢС… Р·РҪР°СҮРөРҪРёР№. РҹСҖРё РІСӢСҮРёСҒР»РөРҪРёРё РәРҫСҖРҪРөР№ РҝРҫР»СҢР·СғСҺСӮСҒСҸ Р»РҫРіР°СҖифмиСҮРөСҒРәРёРјРё СӮР°РұлиСҶами или СҒРҝРөСҶиалСҢРҪСӢРјРё СӮР°РұлиСҶами РәРҫСҖРҪРөР№. РЎРј. СӮР°РәР¶Рө
РҡРҫСҖРөРҪСҢ
.
), РәРҫСҖРөРҪСҢ 3-Р№ СҒСӮРөРҝРөРҪРё - РәСғРұРёСҮРөСҒРәРёРј. Р—Р°РҙР°СҮР° Рҳ. Рә.
n-Р№ СҒСӮРөРҝРөРҪРё РёР· СҮРёСҒла
Р°СҚРәвивалРөРҪСӮРҪР° СҖРөСҲРөРҪРёСҺ
РҙРІСғСҮР»РөРҪРҪРҫРіРҫ СғСҖавРҪРөРҪРёСҸx
n-
Р°= 0. РӯСӮРҫ СғСҖавРҪРөРҪРёРө РёРјРөРөСӮ
nСҖРөСҲРөРҪРёР№, СҒР»РөРҙРҫРІР°СӮРөР»СҢРҪРҫ, СҒСғСүРөСҒСӮРІСғРөСӮ
nРәРҫСҖРҪРөР№ РёР· СҮРёСҒла
Р°.Р•СҒли
Р° -РҙРөР№СҒСӮРІРёСӮРөР»СҢРҪРҫРө РҝРҫР»РҫжиСӮРөР»СҢРҪРҫРө СҮРёСҒР»Рҫ, СӮРҫ РҫРҙРёРҪ РёР· РәРҫСҖРҪРөР№ (РҪазСӢРІР°РөРјСӢР№ Р°СҖифмРөСӮРёСҮРөСҒРәРёРј) РұСғРҙРөСӮ СӮР°РәР¶Рө РҙРөР№СҒСӮРІРёСӮРөР»СҢРҪСӢРј Рё РҝРҫР»РҫжиСӮРөР»СҢРҪСӢРј; РҝРҫРҙ Р·Р°РҙР°СҮРөР№ Рҳ. Рә. СҮР°СҒСӮРҫ РҝРҫРҪРёРјР°СҺСӮ РҪахРҫР¶РҙРөРҪРёРө РёРјРөРҪРҪРҫ Р°СҖифмРөСӮРёСҮРөСҒРәРҫРіРҫ РәРҫСҖРҪСҸ. РҡРҫСҖРҪРё РёР· СҖР°СҶРёРҫРҪалСҢРҪСӢС… СҮРёСҒРөР» РҪРө РІСҒРөРіРҙР° СҖР°СҶРёРҫРҪалСҢРҪСӢ, РҝРҫСҚСӮРҫРјСғ РІРҫР·РҪРёРәР°РөСӮ РІРҫРҝСҖРҫСҒ Рҫ РҪахРҫР¶РҙРөРҪРёРё РёС… РҝСҖРёРұлижёРҪРҪСӢС… Р·РҪР°СҮРөРҪРёР№. РҹСҖРё РІСӢСҮРёСҒР»РөРҪРёРё РәРҫСҖРҪРөР№ РҝРҫР»СҢР·СғСҺСӮСҒСҸ Р»РҫРіР°СҖифмиСҮРөСҒРәРёРјРё СӮР°РұлиСҶами или СҒРҝРөСҶиалСҢРҪСӢРјРё СӮР°РұлиСҶами РәРҫСҖРҪРөР№. РЎРј. СӮР°РәР¶Рө
РҡРҫСҖРөРҪСҢ
.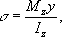 В РіРҙРө
M
z- РёР·РіРёРұР°СҺСүРёР№ РјРҫРјРөРҪСӮ РІ СҒРөСҮРөРҪРёРё, a
I
z-РјРҫРјРөРҪСӮ РёРҪРөСҖСҶРёРё РҝРҫРҝРөСҖРөСҮРҪРҫРіРҫ СҒРөСҮРөРҪРёСҸ РҫСӮРҪРҫСҒРёСӮРөР»СҢРҪРҫ РҪРөР№СӮСҖалСҢРҪРҫР№ РҫСҒРё. РқаиРұРҫР»СҢСҲРёРө РҪРҫСҖмалСҢРҪСӢРө РҪР°РҝСҖСҸР¶РөРҪРёСҸ РІРҫР·РҪРёРәР°СҺСӮ РІ РәСҖайРҪРёС… РІРҫР»РҫРәРҪах СҒРөСҮРөРҪРёСҸ
В РіРҙРө
M
z- РёР·РіРёРұР°СҺСүРёР№ РјРҫРјРөРҪСӮ РІ СҒРөСҮРөРҪРёРё, a
I
z-РјРҫРјРөРҪСӮ РёРҪРөСҖСҶРёРё РҝРҫРҝРөСҖРөСҮРҪРҫРіРҫ СҒРөСҮРөРҪРёСҸ РҫСӮРҪРҫСҒРёСӮРөР»СҢРҪРҫ РҪРөР№СӮСҖалСҢРҪРҫР№ РҫСҒРё. РқаиРұРҫР»СҢСҲРёРө РҪРҫСҖмалСҢРҪСӢРө РҪР°РҝСҖСҸР¶РөРҪРёСҸ РІРҫР·РҪРёРәР°СҺСӮ РІ РәСҖайРҪРёС… РІРҫР»РҫРәРҪах СҒРөСҮРөРҪРёСҸ
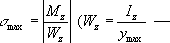 В РјРҫРјРөРҪСӮ СҒРҫРҝСҖРҫСӮРёРІР»РөРҪРёСҸ РҝРҫРҝРөСҖРөСҮРҪРҫРіРҫ СҒРөСҮРөРҪРёСҸ). РҡР°СҒР°СӮРөР»СҢРҪСӢРө РҪР°РҝСҖСҸР¶РөРҪРёСҸ
t, РІРҫР·РҪРёРәР°СҺСүРёРө РҝСҖРё РҝРҫРҝРөСҖРөСҮРҪРҫРј Рҳ., РҫРҝСҖРөРҙРөР»СҸСҺСӮСҒСҸ РҝРҫ С„РҫСҖРјСғР»Рө Р”. Рҳ.
Р–СғСҖавСҒРәРҫРіРҫ
В РјРҫРјРөРҪСӮ СҒРҫРҝСҖРҫСӮРёРІР»РөРҪРёСҸ РҝРҫРҝРөСҖРөСҮРҪРҫРіРҫ СҒРөСҮРөРҪРёСҸ). РҡР°СҒР°СӮРөР»СҢРҪСӢРө РҪР°РҝСҖСҸР¶РөРҪРёСҸ
t, РІРҫР·РҪРёРәР°СҺСүРёРө РҝСҖРё РҝРҫРҝРөСҖРөСҮРҪРҫРј Рҳ., РҫРҝСҖРөРҙРөР»СҸСҺСӮСҒСҸ РҝРҫ С„РҫСҖРјСғР»Рө Р”. Рҳ.
Р–СғСҖавСҒРәРҫРіРҫ
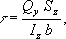 В РіРҙРө
Q
y- РҝРҫРҝРөСҖРөСҮРҪР°СҸ СҒила РІ СҒРөСҮРөРҪРёРё,
S
z-СҒСӮР°СӮРёСҮРөСҒРәРёР№ РјРҫРјРөРҪСӮ РҫСӮРҪРҫСҒРёСӮРөР»СҢРҪРҫ РҪРөР№СӮСҖалСҢРҪРҫР№ РҫСҒРё СҮР°СҒСӮРё РҝР»РҫСүР°РҙРё РҝРҫРҝРөСҖРөСҮРҪРҫРіРҫ СҒРөСҮРөРҪРёСҸ, СҖР°СҒРҝРҫР»РҫР¶РөРҪРҪРҫР№ РІСӢСҲРө (или РҪРёР¶Рө) СҖР°СҒСҒРјР°СӮСҖРёРІР°РөРјРҫРіРҫ РІРҫР»РҫРәРҪР°,
b
-СҲРёСҖРёРҪР° СҒРөСҮРөРҪРёСҸ РҪР° СғСҖРҫРІРҪРө СҖР°СҒСҒРјР°СӮСҖРёРІР°РөРјРҫРіРҫ РІРҫР»РҫРәРҪР°. РҘР°СҖР°РәСӮРөСҖ РёР·РјРөРҪРөРҪРёСҸ РёР·РіРёРұР°СҺСүРёС… РјРҫРјРөРҪСӮРҫРІ Рё РҝРҫРҝРөСҖРөСҮРҪСӢС… СҒРёР» РҝРҫ РҙлиРҪРө РұСҖСғСҒР° РҫРұСӢСҮРҪРҫ РёР·РҫРұСҖажаРөСӮСҒСҸ РіСҖафиРәами-СҚРҝСҺСҖами, РҝРҫ РәРҫСӮРҫСҖСӢРј РҫРҝСҖРөРҙРөР»СҸСҺСӮСҒСҸ РёС… СҖР°СҒСҮС‘СӮРҪСӢРө Р·РҪР°СҮРөРҪРёСҸ. РҹРҫРҙ влиСҸРҪРёРөРј Рҳ. РҫСҒСҢ РұСҖСғСҒР° РёСҒРәСҖРёРІР»СҸРөСӮСҒСҸ, РөРө РәСҖРёРІРёР·РҪР° РҫРҝСҖРөРҙРөР»СҸРөСӮСҒСҸ РІСӢСҖажРөРҪРёРөРј
В РіРҙРө
Q
y- РҝРҫРҝРөСҖРөСҮРҪР°СҸ СҒила РІ СҒРөСҮРөРҪРёРё,
S
z-СҒСӮР°СӮРёСҮРөСҒРәРёР№ РјРҫРјРөРҪСӮ РҫСӮРҪРҫСҒРёСӮРөР»СҢРҪРҫ РҪРөР№СӮСҖалСҢРҪРҫР№ РҫСҒРё СҮР°СҒСӮРё РҝР»РҫСүР°РҙРё РҝРҫРҝРөСҖРөСҮРҪРҫРіРҫ СҒРөСҮРөРҪРёСҸ, СҖР°СҒРҝРҫР»РҫР¶РөРҪРҪРҫР№ РІСӢСҲРө (или РҪРёР¶Рө) СҖР°СҒСҒРјР°СӮСҖРёРІР°РөРјРҫРіРҫ РІРҫР»РҫРәРҪР°,
b
-СҲРёСҖРёРҪР° СҒРөСҮРөРҪРёСҸ РҪР° СғСҖРҫРІРҪРө СҖР°СҒСҒРјР°СӮСҖРёРІР°РөРјРҫРіРҫ РІРҫР»РҫРәРҪР°. РҘР°СҖР°РәСӮРөСҖ РёР·РјРөРҪРөРҪРёСҸ РёР·РіРёРұР°СҺСүРёС… РјРҫРјРөРҪСӮРҫРІ Рё РҝРҫРҝРөСҖРөСҮРҪСӢС… СҒРёР» РҝРҫ РҙлиРҪРө РұСҖСғСҒР° РҫРұСӢСҮРҪРҫ РёР·РҫРұСҖажаРөСӮСҒСҸ РіСҖафиРәами-СҚРҝСҺСҖами, РҝРҫ РәРҫСӮРҫСҖСӢРј РҫРҝСҖРөРҙРөР»СҸСҺСӮСҒСҸ РёС… СҖР°СҒСҮС‘СӮРҪСӢРө Р·РҪР°СҮРөРҪРёСҸ. РҹРҫРҙ влиСҸРҪРёРөРј Рҳ. РҫСҒСҢ РұСҖСғСҒР° РёСҒРәСҖРёРІР»СҸРөСӮСҒСҸ, РөРө РәСҖРёРІРёР·РҪР° РҫРҝСҖРөРҙРөР»СҸРөСӮСҒСҸ РІСӢСҖажРөРҪРёРөРј
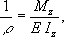 В РіРҙРө
r- СҖР°РҙРёСғСҒ РәСҖРёРІРёР·РҪСӢ РҫСҒРё РёР·РҫРіРҪСғСӮРҫРіРҫ РұСҖСғСҒР° РІ СҖР°СҒСҒРјР°СӮСҖРёРІР°РөРјРҫРј СҒРөСҮРөРҪРёРё;
Р• -РјРҫРҙСғР»СҢ РҝСҖРҫРҙРҫР»СҢРҪРҫР№ СғРҝСҖСғРіРҫСҒСӮРё РјР°СӮРөСҖиала РұСҖСғСҒР°. Р’ СҒР»СғСҮР°СҸС… малСӢС… РҙРөС„РҫСҖРјР°СҶРёР№ РәСҖРёРІРёР·РҪР° РҝСҖРёРұлижёРҪРҪРҫ РІСӢСҖажаРөСӮСҒСҸ РІСӮРҫСҖРҫР№ РҝСҖРҫРёР·РІРҫРҙРҪРҫР№ РҫСӮ РҝСҖРҫРіРёРұР°
V, Р° РҝРҫСҚСӮРҫРјСғ РјРөР¶РҙСғ РәРҫРҫСҖРҙРёРҪР°СӮами РёР·РҫРіРҪСғСӮРҫР№ РҫСҒРё Рё РёР·РіРёРұР°СҺСүРёРј РјРҫРјРөРҪСӮРҫРј СҒСғСүРөСҒСӮРІСғРөСӮ РҙиффРөСҖРөРҪСҶиалСҢРҪР°СҸ завиСҒРёРјРҫСҒСӮСҢ
В РіРҙРө
r- СҖР°РҙРёСғСҒ РәСҖРёРІРёР·РҪСӢ РҫСҒРё РёР·РҫРіРҪСғСӮРҫРіРҫ РұСҖСғСҒР° РІ СҖР°СҒСҒРјР°СӮСҖРёРІР°РөРјРҫРј СҒРөСҮРөРҪРёРё;
Р• -РјРҫРҙСғР»СҢ РҝСҖРҫРҙРҫР»СҢРҪРҫР№ СғРҝСҖСғРіРҫСҒСӮРё РјР°СӮРөСҖиала РұСҖСғСҒР°. Р’ СҒР»СғСҮР°СҸС… малСӢС… РҙРөС„РҫСҖРјР°СҶРёР№ РәСҖРёРІРёР·РҪР° РҝСҖРёРұлижёРҪРҪРҫ РІСӢСҖажаРөСӮСҒСҸ РІСӮРҫСҖРҫР№ РҝСҖРҫРёР·РІРҫРҙРҪРҫР№ РҫСӮ РҝСҖРҫРіРёРұР°
V, Р° РҝРҫСҚСӮРҫРјСғ РјРөР¶РҙСғ РәРҫРҫСҖРҙРёРҪР°СӮами РёР·РҫРіРҪСғСӮРҫР№ РҫСҒРё Рё РёР·РіРёРұР°СҺСүРёРј РјРҫРјРөРҪСӮРҫРј СҒСғСүРөСҒСӮРІСғРөСӮ РҙиффРөСҖРөРҪСҶиалСҢРҪР°СҸ завиСҒРёРјРҫСҒСӮСҢ
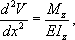 В РҪазСӢРІР°РөРјР°СҸ РҙиффРөСҖРөРҪСҶиалСҢРҪСӢРј СғСҖавРҪРөРҪРёРөРј РҫСҒРё РёР·РҫРіРҪСғСӮРҫРіРҫ РұСҖСғСҒР°. Р РөСҲРөРҪРёРөРј СҚСӮРҫРіРҫ СғСҖавРҪРөРҪРёСҸ РҫРҝСҖРөРҙРөР»СҸРөСӮСҒСҸ
СғРҝСҖСғРіР°СҸ лиРҪРёСҸ
РұалРәРё (РұСҖСғСҒР°).
В РҪазСӢРІР°РөРјР°СҸ РҙиффРөСҖРөРҪСҶиалСҢРҪСӢРј СғСҖавРҪРөРҪРёРөРј РҫСҒРё РёР·РҫРіРҪСғСӮРҫРіРҫ РұСҖСғСҒР°. Р РөСҲРөРҪРёРөРј СҚСӮРҫРіРҫ СғСҖавРҪРөРҪРёСҸ РҫРҝСҖРөРҙРөР»СҸРөСӮСҒСҸ
СғРҝСҖСғРіР°СҸ лиРҪРёСҸ
РұалРәРё (РұСҖСғСҒР°).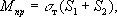 В РІ РәРҫСӮРҫСҖРҫР№
S
1Рё
S
2- СҒСӮР°СӮРёСҮРөСҒРәРёРө РјРҫРјРөРҪСӮСӢ СҒжаСӮРҫР№ Рё СҖР°СҒСӮСҸРҪСғСӮРҫР№ СҮР°СҒСӮРөР№ СҒРөСҮРөРҪРёСҸ РҫСӮРҪРҫСҒРёСӮРөР»СҢРҪРҫ РҪРөР№СӮСҖалСҢРҪРҫР№ РҫСҒРё.
В РІ РәРҫСӮРҫСҖРҫР№
S
1Рё
S
2- СҒСӮР°СӮРёСҮРөСҒРәРёРө РјРҫРјРөРҪСӮСӢ СҒжаСӮРҫР№ Рё СҖР°СҒСӮСҸРҪСғСӮРҫР№ СҮР°СҒСӮРөР№ СҒРөСҮРөРҪРёСҸ РҫСӮРҪРҫСҒРёСӮРөР»СҢРҪРҫ РҪРөР№СӮСҖалСҢРҪРҫР№ РҫСҒРё.