 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ИЗ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ИЗ) - Чтение (стр. 26)
В Р Р°СҒРҝР°Рҙ РёР·РҫРјРөСҖРҫРІ СҮР°СүРө РІСҒРөРіРҫ СҒРҫРҝСҖРҫРІРҫР¶РҙР°РөСӮСҒСҸ РёСҒРҝСғСҒРәР°РҪРёРөРј РәРҫРҪРІРөСҖСҒРёРҫРҪРҪСӢС… СҚР»РөРәСӮСҖРҫРҪРҫРІ (СҒРј. РҡРҫРҪРІРөСҖСҒРёСҸ РІРҪСғСӮСҖРөРҪРҪСҸСҸ ) или g-РәРІР°РҪСӮРҫРІ; РІ СҖРөР·СғР»СҢСӮР°СӮРө РҫРұСҖазСғРөСӮСҒСҸ СҸРҙСҖРҫ СӮРҫРіРҫ Р¶Рө РёР·РҫСӮРҫРҝР°, РҪРҫ РІ РұРҫР»РөРө РҪРёР·РәРҫРј СҚРҪРөСҖРіРөСӮРёСҮРөСҒРәРҫРј СҒРҫСҒСӮРҫСҸРҪРёРё. РҳРҪРҫРіРҙР° РұРҫР»РөРө РІРөСҖРҫСҸСӮРҪСӢРј СҸРІР»СҸРөСӮСҒСҸ РұРөСӮР°-СҖР°СҒРҝР°Рҙ , РәРҫСӮРҫСҖСӢР№ РҝСҖРёРІРҫРҙРёСӮ Рә РІРҫР·РҪРёРәРҪРҫРІРөРҪРёСҺ РёР·РҫСӮРҫРҝР° РҙСҖСғРіРҫРіРҫ СҚР»РөРјРөРҪСӮР° ( СҖРёСҒ. ). РҳР·РҫРјРөСҖСӢ СӮСҸжёлСӢС… СҚР»РөРјРөРҪСӮРҫРІ РјРҫРіСғСӮ СҖР°СҒРҝР°РҙР°СӮСҢСҒСҸ РҝСғСӮём СҒамРҫРҝСҖРҫРёР·РІРҫР»СҢРҪРҫРіРҫ РҙРөР»РөРҪРёСҸ (СҒРј. РҜРҙСҖР° Р°СӮРҫРјРҪРҫРіРҫ РҙРөР»РөРҪРёРө ). В Рҳ. Р°. СҸ. РҫРұСғСҒР»РҫРІР»РөРҪР° РҫСҒРҫРұРөРҪРҪРҫСҒСӮСҸРјРё СҒСӮСҖСғРәСӮСғСҖСӢ Р°СӮРҫРјРҪСӢС… СҸРҙРөСҖ. РҳР·РҫРјРөСҖРҪСӢРө СҒРҫСҒСӮРҫСҸРҪРёСҸ РҫРұСҖазСғСҺСӮСҒСҸ РІ СӮРөС… СҒР»СғСҮР°СҸС…, РәРҫРіРҙР° РҝРөСҖРөС…РҫРҙ СҸРҙСҖР° РёР· СҒРҫСҒСӮРҫСҸРҪРёСҸ СҒ РұРҫР»СҢСҲРөР№ СҚРҪРөСҖРіРёРөР№ РІ РұРҫР»РөРө РҪРёР·РәРҫРө СҚРҪРөСҖРіРөСӮРёСҮРөСҒРәРҫРө СҒРҫСҒСӮРҫСҸРҪРёРө РҝСғСӮём РёСҒРҝСғСҒРәР°РҪРёСҸ g-РәРІР°РҪСӮР° Р·Р°СӮСҖСғРҙРҪС‘РҪ. ЧаСүРө РІСҒРөРіРҫ СҚСӮРҫ СҒРІСҸР·Р°РҪРҫ СҒ РұРҫР»СҢСҲРёРј СҖазлиСҮРёРөРј РІ Р·РҪР°СҮРөРҪРёСҸС… СҒРҝРёРҪРҫРІ S СҸРҙРөСҖ РІ СҚСӮРёС… СҒРҫСҒСӮРҫСҸРҪРёСҸС…. Р•СҒли РҝСҖРё СҚСӮРҫРј СҖазлиСҮРёРө СҚРҪРөСҖРіРёРё РІ РҙРІСғС… СҒРҫСҒСӮРҫСҸРҪРёСҸС… РҪРөРІРөлиРәРҫ, СӮРҫ РІРөСҖРҫСҸСӮРҪРҫСҒСӮСҢ РёСҒРҝСғСҒРәР°РҪРёСҸ g-РәРІР°РҪСӮР° СҒСӮР°РҪРҫРІРёСӮСҒСҸ малРҫР№ Рё, РәР°Рә СҒР»РөРҙСҒСӮРІРёРө, РҝРөСҖРёРҫРҙ РҝРҫР»СғСҖР°СҒРҝР°РҙР° РІРҫР·РұСғР¶РҙС‘РҪРҪРҫРіРҫ СҒРҫСҒСӮРҫСҸРҪРёСҸ РҫРәазСӢРІР°РөСӮСҒСҸ РұРҫР»СҢСҲРёРј. РҳР·РҫРјРөСҖСӢ РҫСҒРҫРұРөРҪРҪРҫ СҮР°СҒСӮРҫ РІСҒСӮСҖРөСҮР°СҺСӮСҒСҸ Сғ СҸРҙРөСҖ РІ РҫРҝСҖРөРҙРөлёРҪРҪСӢС… РҫРұлаСҒСӮСҸС… Р·РҪР°СҮРөРҪРёР№ РјР°СҒСҒРҫРІСӢС… СҮРёСҒРөР» (РҫСҒСӮСҖРҫРІР° РёР·РҫРјРөСҖРёРё). РӯСӮРҫСӮ фаРәСӮ РҫРұСҠСҸСҒРҪСҸРөСӮ РҫРұРҫР»РҫСҮРөСҮРҪР°СҸ РјРҫРҙРөР»СҢ СҸРҙСҖР°, РәРҫСӮРҫСҖР°СҸ РҝСҖРөРҙСҒРәазСӢРІР°РөСӮ СҒСғСүРөСҒСӮРІРҫРІР°РҪРёРө РұлизРәРёС… РҝРҫ СҚРҪРөСҖРіРёРё СҸРҙРөСҖРҪСӢС… СғСҖРҫРІРҪРөР№ СҒ РұРҫР»СҢСҲРёРј СҖазлиСҮРёРөРј СҒРҝРёРҪРҫРІ РҝСҖРё РҫРҝСҖРөРҙРөлёРҪРҪСӢС… Р·РҪР°СҮРөРҪРёСҸС… СҮРёСҒРөР» РҝСҖРҫСӮРҫРҪРҫРІ Рё РҪРөР№СӮСҖРҫРҪРҫРІ, РІС…РҫРҙСҸСүРёС… РІ СҒРҫСҒСӮав СҸРҙСҖР° (СҒРј. РҜРҙРөСҖРҪСӢРө РјРҫРҙРөли ). Р’ РҪРөРәРҫСӮРҫСҖСӢС… СҒР»СғСҮР°СҸС… (РҪР°РҝСҖРёРјРөСҖ, РҙР»СҸ 180Hf) РІРҫР·РҪРёРәРҪРҫРІРөРҪРёРө РёР·РҫРјРөСҖРҫРІ СҒРІСҸР·Р°РҪРҫ СҒ СҒСғСүРөСҒСӮРІРөРҪРҪСӢРј СҖазлиСҮРёРөРј С„РҫСҖРјСӢ СҸРҙСҖР° РІ РҙРІСғС… РұлизРәРёС… СҚРҪРөСҖРіРөСӮРёСҮРөСҒРәРёС… СҒРҫСҒСӮРҫСҸРҪРёСҸС…, СҮСӮРҫ СӮР°РәР¶Рө РҝСҖРёРІРҫРҙРёСӮ Рә СғРјРөРҪСҢСҲРөРҪРёСҺ РІРөСҖРҫСҸСӮРҪРҫСҒСӮРё g-РёР·Р»СғСҮРөРҪРёСҸ. В РӣРёСӮ.:РңСғС…РёРҪ Рҡ. Рқ., Р’РІРөРҙРөРҪРёРө РІ СҸРҙРөСҖРҪСғСҺ физиРәСғ, Рң., 1963; РңРҫСҲРәРҫРІСҒРәРёР№ РЎ., РўРөРҫСҖРёСҸ РјСғР»СҢСӮРёРҝРҫР»СҢРҪРҫРіРҫ РёР·Р»СғСҮРөРҪРёСҸ, РІ РәРҪ.: РҗР»СҢфа-, РұРөСӮР°- Рё гамма-СҒРҝРөРәСӮСҖРҫСҒРәРҫРҝРёСҸ, РҝРҫРҙ СҖРөРҙ. Рҡ. Р—РёРіРұР°РҪР°, РҝРөСҖ. СҒ Р°РҪРіР»., РІ. 3, Рң., 1969, СҒ. 5. В Рқ. Рқ. Р”РөР»СҸРіРёРҪ. 
Р РёСҒ. Рә СҒСӮР°СӮСҢРө РҳР·РҫРјРөСҖРёСҸ Р°СӮРҫРјРҪСӢС… СҸРҙРөСҖ. РҳР·РҫРјРөСҖСӢ РҳР·РҫРјРө'СҖСӢ,С…РёРјРёСҮРөСҒРәРёРө СҒРҫРөРҙРёРҪРөРҪРёСҸ, РҫРҙРёРҪР°РәРҫРІСӢРө РҝРҫ СҒРҫСҒСӮавСғ Рё РјРҫР»РөРәСғР»СҸСҖРҪРҫР№ РјР°СҒСҒРө, РҪРҫ СҖазлиСҮР°СҺСүРёРөСҒСҸ РҝРҫ СҒСӮСҖРҫРөРҪРёСҺ Рё СҒРІРҫР№СҒСӮвам (С…РёРјРёСҮРөСҒРәРёРј Рё физиСҮРөСҒРәРёРј). РҹРҫРҙСҖРҫРұРҪРөРө СҒРј. РҳР·РҫРјРөСҖРёСҸ С…РёРјРёСҮРөСҒРәРёС… СҒРҫРөРҙРёРҪРөРҪРёР№. Рһ СҸРҙРөСҖРҪСӢС… Рҳ. СҒРј. РҳР·РҫРјРөСҖРёСҸ Р°СӮРҫРјРҪСӢС… СҸРҙРөСҖ. РҳР·РҫРјРөСӮСҖРёСҮРөСҒРәРҫРө РјСӢСҲРөСҮРҪРҫРө СҒРҫРәСҖР°СүРөРҪРёРө РҳР·РҫРјРөСӮСҖРё'СҮРөСҒРәРҫРө РјСӢ'СҲРөСҮРҪРҫРө СҒРҫРәСҖР°СүРө'РҪРёРө,СҒРҫРәСҖР°СүРөРҪРёРө РјСӢСҲСҶСӢ, РІСӢСҖажаСҺСүРөРөСҒСҸ РІ СғСҒРёР»РөРҪРёРё РөС‘ РҪР°РҝСҖСҸР¶РөРҪРёСҸ РҝСҖРё РҪРөРёР·РјРөРҪРҪРҫР№ РҙлиРҪРө (РҪР°РҝСҖРёРјРөСҖ, СҒРҫРәСҖР°СүРөРҪРёРө РјСӢСҲСҶСӢ РәРҫРҪРөСҮРҪРҫСҒСӮРё, РҫРұР° РәРҫРҪСҶР° РәРҫСӮРҫСҖРҫР№ Р·Р°РәСҖРөРҝР»РөРҪСӢ РҪРөРҝРҫРҙРІРёР¶РҪРҫ). Р’ РҫСҖРіР°РҪРёР·РјРө Рә Рҳ. Рј. СҒ. РҝСҖРёРұлижаРөСӮСҒСҸ РҪР°РҝСҖСҸР¶РөРҪРёРө, СҖазвиваРөРјРҫРө РјСӢСҲСҶРөР№ РҝСҖРё РҝРҫРҝСӢСӮРәРө РҝРҫРҙРҪСҸСӮСҢ РҪРөРҝРҫСҒРёР»СҢРҪСӢР№ РіСҖСғР·. РЎСҖ. РҳР·РҫСӮРҫРҪРёСҮРөСҒРәРҫРө РјСӢСҲРөСҮРҪРҫРө СҒРҫРәСҖР°СүРөРҪРёРө. РҳР·РҫРјРөСӮСҖРёСҸ РҳР·РҫРјРө'СӮСҖРё'СҸ(РҫСӮ РёР·Рҫ... Рё ...РјРөСӮСҖРёСҸ ) РІ РұРёРҫР»РҫРіРёРё, СҒРҫС…СҖР°РҪРөРҪРёРө РҝСҖРҫРҝРҫСҖСҶРёР№ РҫСҖРіР°РҪРҫРІ Рё СҮР°СҒСӮРөР№ СӮРөла РІ РҝРөСҖРёРҫРҙ СҖРҫСҒСӮР° РҫСҖРіР°РҪРёР·РјР°. РҳР·РҫРјРҫСҖфизм (РјР°СӮРөРј.) РҳР·РҫРјРҫСҖфи'Р·Рј,РҫРҙРҪРҫ РёР· РҫСҒРҪРҫРІРҪСӢС… РҝРҫРҪСҸСӮРёР№ СҒРҫРІСҖРөРјРөРҪРҪРҫР№ РјР°СӮРөРјР°СӮРёРәРё, РІРҫР·РҪРёРәСҲРөРө СҒРҪР°СҮала РІ РҝСҖРөРҙРөлах алгРөРұСҖСӢ РІ РҝСҖРёРјРөРҪРөРҪРёРё Рә СӮР°РәРёРј алгРөРұСҖаиСҮРөСҒРәРёРј РҫРұСҖазРҫРІР°РҪРёСҸРј, РәР°Рә РіСҖСғРҝРҝСӢ , РәРҫР»СҢСҶР° , РҝРҫР»СҸ Рё СӮ. Рҝ., РҪРҫ РҫРәазавСҲРөРөСҒСҸ РІРөСҒСҢРјР° СҒСғСүРөСҒСӮРІРөРҪРҪСӢРј РҙР»СҸ РҫРұСүРөРіРҫ РҝРҫРҪРёРјР°РҪРёСҸ СҒСӮСҖРҫРөРҪРёСҸ Рё РҫРұлаСҒСӮРё РІРҫР·РјРҫР¶РҪСӢС… РҝСҖРёРјРөРҪРөРҪРёР№ РәажРҙРҫРіРҫ СҖазРҙРөла РјР°СӮРөРјР°СӮРёРәРё. В РҹРҫРҪСҸСӮРёРө Рҳ. РҫСӮРҪРҫСҒРёСӮСҒСҸ Рә СҒРёСҒСӮРөмам РҫРұСҠРөРәСӮРҫРІ СҒ Р·Р°РҙР°РҪРҪСӢРјРё РІ РҪРёС… РҫРҝРөСҖР°СҶРёСҸРјРё или РҫСӮРҪРҫСҲРөРҪРёСҸРјРё. Р’ РәР°СҮРөСҒСӮРІРө РҝСҖРҫСҒСӮРҫРіРҫ РҝСҖРёРјРөСҖР° РҙРІСғС… РёР·РҫРјРҫСҖС„РҪСӢС… СҒРёСҒСӮРөРј РјРҫР¶РҪРҫ СҖР°СҒСҒРјРҫСӮСҖРөСӮСҢ СҒРёСҒСӮРөРјСғ
RРІСҒРөС… РҙРөР№СҒСӮРІРёСӮРөР»СҢРҪСӢС… СҮРёСҒРөР» СҒ Р·Р°РҙР°РҪРҪРҫР№ РҪР° РҪРөР№ РҫРҝРөСҖР°СҶРёРөР№ СҒР»РҫР¶РөРҪРёСҸ
x=
x
1+
x
1Рё СҒРёСҒСӮРөРјСғ
Р РҝРҫР»РҫжиСӮРөР»СҢРҪСӢС… РҙРөР№СҒСӮРІРёСӮРөР»СҢРҪСӢС… СҮРёСҒРөР» СҒ Р·Р°РҙР°РҪРҪРҫР№ РҪР° РҪРөР№ РҫРҝРөСҖР°СҶРёРөР№ СғРјРҪРҫР¶РөРҪРёСҸ
y=
y
1
y
2
.РңРҫР¶РҪРҫ РҝРҫРәазаСӮСҢ, СҮСӮРҫ РІРҪСғСӮСҖРөРҪРҪРөРө В«СғСҒСӮСҖРҫР№СҒСӮРІРҫВ» СҚСӮРёС… РҙРІСғС… СҒРёСҒСӮРөРј СҮРёСҒРөР» СҒРҫРІРөСҖСҲРөРҪРҪРҫ РҫРҙРёРҪР°РәРҫРІРҫ. ДлСҸ СҚСӮРҫРіРҫ РҙРҫСҒСӮР°СӮРҫСҮРҪРҫ СҒРёСҒСӮРөРјСғ
RРҫСӮРҫРұСҖазиСӮСҢ РІ СҒРёСҒСӮРөРјСғ
Р , РҝРҫСҒСӮавив РІ СҒРҫРҫСӮРІРөСӮСҒСӮРІРёРө СҮРёСҒР»Сғ
С…РёР·
RСҮРёСҒР»Рҫ
Сғ=
a
x
(
Р°> 1) РёР· Р . РўРҫРіРҙР° СҒСғРјРјРө
x=
x
1
+
x
2РұСғРҙРөСӮ СҒРҫРҫСӮРІРөСӮСҒСӮРІРҫРІР°СӮСҢ РҝСҖРҫРёР·РІРөРҙРөРҪРёРө
y=
y
1
y
2СҮРёСҒРөР»
СҮР»РөРҪРҫРІ Р°СҖифмРөСӮРёСҮРөСҒРәРҫР№ РҝСҖРҫРіСҖРөСҒСҒРёРё РІСӢСҖажаРөСӮСҒСҸ С„РҫСҖРјСғР»РҫР№
СӮРҫ РІ Р РҝСҖРҫРёР·РІРөРҙРөРҪРёРө
СҮР»РөРҪРҫРІ РіРөРҫРјРөСӮСҖРёСҮРөСҒРәРҫР№ РҝСҖРҫРіСҖРөСҒСҒРёРё РІСӢСҖажаРөСӮСҒСҸ С„РҫСҖРјСғР»РҫР№
(СғРјРҪРҫР¶РөРҪРёСҺ РҪР° nРІ СҒРёСҒСӮРөРјРө RСҒРҫРҫСӮРІРөСӮСҒСӮРІСғРөСӮ РҝСҖРё РҝРөСҖРөС…РҫРҙРө Рә СҒРёСҒСӮРөРјРө Р РІРҫР·РІРөРҙРөРҪРёРө РІ n-СҺ СҒСӮРөРҝРөРҪСҢ, Р° РҙРөР»РөРҪРёСҺ РҪР° РҙРІР° - РёР·РІР»РөСҮРөРҪРёРө РәРІР°РҙСҖР°СӮРҪРҫРіРҫ РәРҫСҖРҪСҸ). В РҳР·СғСҮРөРҪРёРө СҒРІРҫР№СҒСӮРІ РҫРҙРҪРҫР№ РёР· РёР·РҫРјРҫСҖС„РҪСӢС… СҒРёСҒСӮРөРј РІ Р·РҪР°СҮРёСӮРөР»СҢРҪРҫР№ РјРөСҖРө (Р° СҒ Р°РұСҒСӮСҖР°РәСӮРҪРҫ-РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ СӮРҫСҮРәРё Р·СҖРөРҪРёСҸ - РҝРҫР»РҪРҫСҒСӮСҢСҺ) СҒРІРҫРҙРёСӮСҒСҸ Рә РёР·СғСҮРөРҪРёСҺ СҒРІРҫР№СҒСӮРІ РҙСҖСғРіРҫР№. РӣСҺРұСғСҺ СҒРёСҒСӮРөРјСғ РҫРұСҠРөРәСӮРҫРІ S',РёР·РҫРјРҫСҖС„РҪСғСҺ СҒРёСҒСӮРөРјРө S, РјРҫР¶РҪРҫ СҖР°СҒСҒРјР°СӮСҖРёРІР°СӮСҢ РәР°Рә «мРҫРҙРөР»СҢВ» СҒРёСҒСӮРөРјСӢ S(«мРҫРҙРөлиСҖРҫРІР°СӮСҢ СҒРёСҒСӮРөРјСғ S РҝСҖРё РҝРҫРјРҫСүРё СҒРёСҒСӮРөРјСӢ S'В») Рё СҒРІРҫРҙРёСӮСҢ РёР·СғСҮРөРҪРёРө СҒамСӢС… СҖазРҪРҫРҫРұСҖазРҪСӢС… СҒРІРҫР№СҒСӮРІ СҒРёСҒСӮРөРјСӢ SРә РёР·СғСҮРөРҪРёСҺ СҒРІРҫР№СҒСӮРІ «мРҫРҙРөли» S'. В РһРұСүРөРө РҫРҝСҖРөРҙРөР»РөРҪРёРө Рҳ. СҒРёСҒСӮРөРј РҫРұСҠРөРәСӮРҫРІ СҒ Р·Р°РҙР°РҪРҪСӢРјРё РҪР° РҪРёС… РІ РәРҫРҪРөСҮРҪРҫРј СҮРёСҒР»Рө РҫСӮРҪРҫСҲРөРҪРёСҸРјРё РјРөР¶РҙСғ РҝРҫСҒСӮРҫСҸРҪРҪСӢРј РҙР»СҸ РәажРҙРҫРіРҫ РҫСӮРҪРҫСҲРөРҪРёСҸ СҮРёСҒР»РҫРј РҫРұСҠРөРәСӮРҫРІ СӮР°РәРҫРІРҫ. РҹСғСҒСӮСҢ РҙР°РҪСӢ РҙРІРө СҒРёСҒСӮРөРјСӢ РҫРұСҠРөРәСӮРҫРІ SРё S',РҝСҖРёСҮём РІ РҝРөСҖРІРҫР№ РҫРҝСҖРөРҙРөР»РөРҪСӢ РҫСӮРҪРҫСҲРөРҪРёСҸ
Р° РІРҫ РІСӮРҫСҖРҫР№ - РҫСӮРҪРҫСҲРөРҪРёСҸ
РЎРёСҒСӮРөРјСӢ S Рё S'СҒ СғРәазаРҪРҪСӢРјРё РІ РҪРёС… РҫСӮРҪРҫСҲРөРҪРёСҸРјРё РҪазСӢРІР°СҺСӮСҒСҸ РёР·РҫРјРҫСҖС„РҪСӢРјРё, РөСҒли РёС… РјРҫР¶РҪРҫ РҝРҫСҒСӮавиСӮСҢ РІ СӮР°РәРҫРө взаимРҪРҫ РҫРҙРҪРҫР·РҪР°СҮРҪРҫРө СҒРҫРҫСӮРІРөСӮСҒСӮРІРёРө
(РіРҙРө С… -РҝСҖРҫРёР·РІРҫР»СҢРҪСӢР№ СҚР»РөРјРөРҪСӮ S, Р° x' -РҝСҖРҫРёР·РІРҫР»СҢРҪСӢР№ СҚР»РөРјРөРҪСӮ S'), СҮСӮРҫ РёР· РҪалиСҮРёСҸ F k( x 1, x 2, ...) РІСӢСӮРөРәР°РөСӮ F' k( С…' 1, С…' 2, ...), Рё РҪР°РҫРұРҫСҖРҫСӮ. СамРҫ СғРәазаРҪРҪРҫРө СҒРҫРҫСӮРІРөСӮСҒСӮРІРёРө РҪазСӢРІР°РөСӮСҒСҸ РҝСҖРё СҚСӮРҫРј РёР·РҫРјРҫСҖС„РҪСӢРј РҫСӮРҫРұСҖажРөРҪРёРөРј, или РёР·РҫРјРҫСҖфизмРҫРј. [Р’ РҝСҖРёРІРөРҙС‘РҪРҪРҫРј РІСӢСҲРө РҝСҖРёРјРөСҖРө РІ СҒРёСҒСӮРөРјРө RРҫРҝСҖРөРҙРөР»РөРҪРҫ РҫСӮРҪРҫСҲРөРҪРёРө F( x, x 1 , x 2), РіРҙРө x= x 1+ x 2 ,РІ СҒРёСҒСӮРөРјРө Р - РҫСӮРҪРҫСҲРөРҪРёРө F'( y, y 1, y 2), РіРҙРө Сғ= Сғ 1 Сғ 2; взаимРҪРҫ РҫРҙРҪРҫР·РҪР°СҮРҪРҫРө СҒРҫРҫСӮРІРөСӮСҒСӮРІРёРө СғСҒСӮР°РҪавливаРөСӮСҒСҸ РҝРҫ С„РҫСҖРјСғлам Сғ= a x, С…= 1og ay.] В РҹРҫРҪСҸСӮРёРө Рҳ. РІРҫР·РҪРёРәР»Рҫ РІ СӮРөРҫСҖРёРё РіСҖСғРҝРҝ, РіРҙРө РІРҝРөСҖРІСӢРө РұСӢР» РҝРҫРҪСҸСӮ СӮРҫСӮ фаРәСӮ, СҮСӮРҫ РёР·СғСҮРөРҪРёРө РІРҪСғСӮСҖРөРҪРҪРөР№ СҒСӮСҖСғРәСӮСғСҖСӢ РҙРІСғС… РёР·РҫРјРҫСҖС„РҪСӢС… СҒРёСҒСӮРөРј РҫРұСҠРөРәСӮРҫРІ РҝСҖРөРҙСҒСӮавлСҸРөСӮ СҒРҫРұРҫР№ РҫРҙРҪСғ Рё СӮСғ Р¶Рө Р·Р°РҙР°СҮСғ. В РҗРәСҒРёРҫРјСӢ Р»СҺРұРҫР№ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ СӮРөРҫСҖРёРё РҫРҝСҖРөРҙРөР»СҸСҺСӮ СҒРёСҒСӮРөРјСғ РҫРұСҠРөРәСӮРҫРІ, РёР·СғСҮР°РөРјСғСҺ СҚСӮРҫР№ СӮРөРҫСҖРёРөР№, РІСҒРөРіРҙР° СӮРҫР»СҢРәРҫ СҒ СӮРҫСҮРҪРҫСҒСӮСҢСҺ РҙРҫ Рҳ.: Р°РәСҒРёРҫРјР°СӮРёСҮРөСҒРәРё РҝРҫСҒСӮСҖРҫРөРҪРҪР°СҸ РјР°СӮРөРјР°СӮРёСҮРөСҒРәР°СҸ СӮРөРҫСҖРёСҸ, РҝСҖРёРјРөРҪРёРјР°СҸ Рә РәР°РәРҫР№-лиРұРҫ РҫРҙРҪРҫР№ СҒРёСҒСӮРөРјРө РҫРұСҠРөРәСӮРҫРІ, РІСҒРөРіРҙР° РҝРҫР»РҪРҫСҒСӮСҢСҺ РҝСҖРёРјРөРҪРёРјР° Рё Рә РҙСҖСғРіРҫР№. РҹРҫСҚСӮРҫРјСғ РәажРҙР°СҸ Р°РәСҒРёРҫРјР°СӮРёСҮРөСҒРәРё РёР·Р»РҫР¶РөРҪРҪР°СҸ РјР°СӮРөРјР°СӮРёСҮРөСҒРәР°СҸ СӮРөРҫСҖРёСҸ РҙРҫРҝСғСҒРәР°РөСӮ РҪРө РҫРҙРҪСғ, Р° РјРҪРҫРіРҫ «иРҪСӮРөСҖРҝСҖРөСӮР°СҶРёР№В», или «мРҫРҙРөР»РөР№В» (СҒРј., РҪР°РҝСҖРёРјРөСҖ, РІ СҒСӮ. Р“РөРҫРјРөСӮСҖРёСҸ , СҖазРҙРөР» РҳСҒСӮРҫР»РәРҫРІР°РҪРёРө РіРөРҫРјРөСӮСҖРёРё). В РҹРҫРҪСҸСӮРёРө Рҳ. РІРәР»СҺСҮР°РөСӮ РІ СҒРөРұСҸ РәР°Рә СҮР°СҒСӮРҪСӢР№ СҒР»СғСҮай РҝРҫРҪСҸСӮРёРө РіРҫРјРөРҫРјРҫСҖфизма , РёРіСҖР°СҺСүРөРө РҫСҒРҪРҫРІРҪСғСҺ СҖРҫР»СҢ РІ СӮРҫРҝРҫР»РҫРіРёРё .  ЧаСҒСӮРҪСӢРј СҒР»СғСҮР°РөРј Рҳ. СҸРІР»СҸРөСӮСҒСҸ авСӮРҫРјРҫСҖфизм - взаимРҪРҫ РҫРҙРҪРҫР·РҪР°СҮРҪРҫРө РҫСӮРҫРұСҖажРөРҪРёРө
СҒРёСҒСӮРөРјСӢ РҫРұСҠРөРәСӮРҫРІ СҒ Р·Р°РҙР°РҪРҪСӢРјРё РҫСӮРҪРҫСҲРөРҪРёСҸРјРё F k( x 1, x 2, ...) РҪР° СҒамРҫС‘ СҒРөРұСҸ, РҝСҖРё РәРҫСӮРҫСҖРҫРј РёР· F k( x 1, x 2, ...) РІСӢСӮРөРәР°РөСӮ F' k( x' 1, x' 2, ...), Рё РҪР°РҫРұРҫСҖРҫСӮ. РӯСӮРҫ РҝРҫРҪСҸСӮРёРө СӮРҫР¶Рө РІРҫР·РҪРёРәР»Рҫ РІ СӮРөРҫСҖРёРё РіСҖСғРҝРҝ, РҪРҫ РҝРҫСӮРҫРј РҫРәазалРҫСҒСҢ СҒСғСүРөСҒСӮРІРөРҪРҪСӢРј РІ СҒамСӢС… СҖазлиСҮРҪСӢС… СҖазРҙРөлах РјР°СӮРөРјР°СӮРёРәРё. В РӣРёСӮ.:РҡСғСҖРҫСҲ Рҗ. Р“., РҡСғСҖСҒ РІСӢСҒСҲРөР№ алгРөРұСҖСӢ, 3 РёР·Рҙ., Рң. - Рӣ., 1952; РӯРҪСҶРёРәР»РҫРҝРөРҙРёСҸ СҚР»РөРјРөРҪСӮР°СҖРҪРҫР№ РјР°СӮРөРјР°СӮРёРәРё, РҝРҫРҙ СҖРөРҙ. Рҹ. РЎ. РҗР»РөРәСҒР°РҪРҙСҖРҫРІР° [Рё РҙСҖ.], РәРҪ. 2, Рң. - Рӣ., 1951. РҳР·РҫРјРҫСҖфизм (С…РёРјРёСҮ.)
РҳР·РҫРјРҫСҖфи'Р·Рј(РҫСӮ
РёР·Рҫ...
Рё РіСҖРөСҮ. morphР№ - РІРёРҙ, С„РҫСҖРјР°), СҒРІРҫР№СҒСӮРІРҫ РІРөСүРөСҒСӮРІ, Р°РҪалРҫРіРёСҮРҪСӢС… РҝРҫ С…РёРјРёСҮРөСҒРәРҫРјСғ СҒРҫСҒСӮавСғ, РәСҖРёСҒСӮаллизРҫРІР°СӮСҢСҒСҸ РІ РҫРҙРёРҪР°РәРҫРІСӢС… С„РҫСҖмах. Р’РҝРөСҖРІСӢРө РұСӢР»Рҫ РҝРҫРәазаРҪРҫ РҪРөРјРөСҶРәРёРј РјРёРҪРөСҖалРҫРіРҫРј Рӯ. РңРёСҮРөСҖлихРҫРј (1819) РҪР° РҝСҖРёРјРөСҖРө KH
2PO
4, KH
2AsO
4Рё NH
4H
2PO
4. Р’СҒРәРҫСҖРө РұСӢР»Рҫ РҫРұРҪР°СҖСғР¶РөРҪРҫ, СҮСӮРҫ РҝРөСҖРІСӢРө РҙРІР° РІРөСүРөСҒСӮРІР° РҫРұСҖазСғСҺСӮ СҒРјРөСҲР°РҪРҪСӢРө РәСҖРёСҒСӮаллСӢ (В«СӮРІС‘СҖРҙСӢРө СҖР°СҒСӮРІРҫСҖСӢВ») СҒ РөРҙРёРҪРҫР№ РІРҪРөСҲРҪРөР№ С„РҫСҖРјРҫР№ РҝСҖРё РҝСҖРҫРёР·РІРҫР»СҢРҪРҫРј РҫСӮРҪРҫСҲРөРҪРёРё P : As, РІ СӮРҫ РІСҖРөРјСҸ РәР°Рә РІ РҙСҖСғРіРёС… РҝР°СҖах Р°РҪалРҫРіРёСҮРҪСӢРө замРөСүРөРҪРёСҸ РҫРіСҖР°РҪРёСҮРөРҪСӢ РәРҫлиСҮРөСҒСӮРІРөРҪРҪРҫ. РҹРөСҖРІСӢР№ СҒР»СғСҮай РҫСӮРІРөСҮР°РөСӮ РҝРҫРҪСҸСӮРёСҺ В«СҒРҫРІРөСҖСҲРөРҪРҪСӢР№ Рҳ.В», Р° РІСӮРҫСҖРҫР№ - РҝРҫРҪСҸСӮРёСҺ В«РҫРіСҖР°РҪРёСҮРөРҪРҪСӢР№В», или В«РҪРөСҒРҫРІРөСҖСҲРөРҪРҪСӢР№ Рҳ.В». Р•СҒли РәРҫлиСҮРөСҒСӮРІР° замРөСүР°СҺСүРөРіРҫ СҚР»РөРјРөРҪСӮР° РҪРөРІРөлиРәРё, РҪРҫ СҒСғСүРөСҒСӮРІРөРҪРҪСӢ РҙР»СҸ РҝРҫРёСҒРәРҫРІРёРәР° РјРёРҪРөСҖалРҫРіР°-РіРөРҫС…РёРјРёРәР°, СӮРҫ РіРҫРІРҫСҖСҸСӮ РҫРұ СҚРҪРҙРҫРәСҖРёРҝСӮРёРё (РҝРҫ Рҗ. Р•.
РӨРөСҖСҒРјР°РҪСғ
, замРөСүРөРҪРёРө СғР·Р»РҫРІ РәСҖРёСҒСӮаллиСҮРөСҒРәРёС… СҖРөСҲС‘СӮРҫРә РёРҫРҪами СӮРҫРіРҫ Р¶Рө Р·РҪР°РәР°, РҪРҫ СҖазРҪСӢС… СҒРІРҫР№СҒСӮРІ Рё малРҫ СҒС…РҫРҙРҪСӢС… РІРөлиСҮРёРҪ). РўСҖРөРұРҫРІР°РҪРёРө СҖРҫРҙСҒСӮРІРөРҪРҪРҫСҒСӮРё взаимРҫзамРөСүР°СҺСүРёС…СҒСҸ СҚР»РөРјРөРҪСӮРҫРІ РҝСҖРё Рҳ. РҝРөСҖРІРҫРҪР°СҮалСҢРҪРҫ РҝРҫРҪималРҫСҒСҢ РәР°Рә СҮРёСҒСӮРҫ С…РёРјРёСҮРөСҒРәР°СҸ РұлизРҫСҒСӮСҢ, Рё РҝРөСҖРІСӢРө СҖСҸРҙСӢ РёР·РҫРјРҫСҖС„РҪСӢС… СҚР»РөРјРөРҪСӮРҫРІ (Р’. Рҳ.
Р’РөСҖРҪР°РҙСҒРәРёР№
; СҒРј.
Р“РөРҫС…РёРјРёСҸ
) РҝРҫРІСӮРҫСҖСҸли РіСҖСғРҝРҝСӢ РјРөРҪРҙРөР»РөРөРІСҒРәРҫР№ СҒРёСҒСӮРөРјСӢ СҒ РҪРөРәРҫСӮРҫСҖСӢРјРё РҙРҫРҝРҫР»РҪРөРҪРёСҸРјРё РёР·РІРөСҒСӮРҪСӢС… РёР· Р°РҪалиСӮРёСҮРөСҒРәРҫР№ С…РёРјРёРё РіСҖСғРҝРҝ, РҪР°РҝСҖРёРјРөСҖ Al, Cr, Fe. Р’СӢСҸСҒРҪРёР»РҫСҒСҢ, РҫРҙРҪР°РәРҫ, СҮСӮРҫ РҪРөРІРҫР·РјРҫР¶РҪРҫ, РҪР°РҝСҖРёРјРөСҖ, замРөСүРөРҪРёРө Na РҪР° Rb; СӮРІС‘СҖРҙСӢРө СҖР°СҒСӮРІРҫСҖСӢ Рҡ- Рё Na-coeРҙРёРҪРөРҪРёР№ СҚРҪРөСҖРіРёСҮРҪРҫ СҖР°СҒРҝР°РҙР°СҺСӮСҒСҸ РҝСҖРё РҪРёР·РәРёС… СӮРөРјРҝРөСҖР°СӮСғСҖах (СҖР°СҒРҝР°Рҙ Рҡ-, Na-РҝРҫР»РөРІСӢС… СҲРҝР°СӮРҫРІ). Р РөСҲР°СҺСүРёРј РҙР»СҸ РҫРұСҠСҸСҒРҪРөРҪРёСҸ СҚСӮРёС… СҸРІР»РөРҪРёР№ РҝСҖРё Рҳ. РұСӢР»Рҫ РІРІРөРҙРөРҪРёРө (Р’. Рң.
Р“РҫР»СҢРҙСҲРјРёРҙСӮ
, 1926) РҝСҖРөРҙСҒСӮавлРөРҪРёСҸ РҫРұ
РёРҫРҪРҪСӢС… СҖР°РҙРёСғСҒах
, РұлизРҫСҒСӮСҢ РәРҫСӮРҫСҖСӢС… СҒСӮала РҫРҙРҪРёРј РёР· РҫСҒРҪРҫРІРҪСӢС… СғСҒР»РҫРІРёР№ Рҳ. РЈ РҝРҫР»РҪРҫвалРөРҪСӮРҪСӢС… РәР°СӮРёРҫРҪРҫРІ (Na
1+, Mg
2+,..., S
6+,...) РёРҫРҪРҪСӢР№ СҖР°РҙРёСғСҒ
rРұСӢСҒСӮСҖРҫ СғРјРөРҪСҢСҲР°РөСӮСҒСҸ РІРҙРҫР»СҢ СҒСӮСҖРҫРәРё РјРөРҪРҙРөР»РөРөРІСҒРәРҫР№ СҒРёСҒСӮРөРјСӢ Рё СҖРөР·РәРҫ СғРІРөлиСҮРёРІР°РөСӮСҒСҸ РІРҙРҫР»СҢ РІРөСҖСӮРёРәали РҪР° РІРөлиСҮРёРҪСӢ, РұРҫР»СҢСҲРёРө СҮРөРј 10-15% (СҚРәСҒРҝРөСҖРёРјРөРҪСӮалСҢРҪСӢР№ РҝСҖРөРҙРөР» РҙР»СҸ РІРҫР·РјРҫР¶РҪРҫСҒСӮРё Рҳ.). Р’ СҖРөР·СғР»СҢСӮР°СӮРө РёР·РҫРјРҫСҖС„РҪСӢРјРё РҫРәазСӢРІР°СҺСӮСҒСҸ СҚР»РөРјРөРҪСӮСӢ, СҒРҫСҒРөРҙРҪРёРө РҝРҫ РҙиагРҫРҪалСҸРј (Р”. Рҳ. РңРөРҪРҙРөР»РөРөРІ, Рҗ. Р•. РӨРөСҖСҒРјР°РҪ), РҪР°РҝСҖРёРјРөСҖ СҖСҸРҙ Na-Ca (
r
Na= 0,98
В РһСҒРҫРұРөРҪРҪРҫ СҮР°СҒСӮРҫ РәРҫРјРҝРөРҪСҒР°СҶРёСҸ РҙРҫСҒСӮРёРіР°РөСӮСҒСҸ Р·Р° СҒСҮС‘СӮ РҫРҙРҪРҫРІСҖРөРјРөРҪРҪРҫРіРҫ РіРөСӮРөСҖРҫвалРөРҪСӮРҪРҫРіРҫ Рҳ. «в РҫРұСҖР°СӮРҪРҫРј РҪР°РҝСҖавлРөРҪРёРёВ». Р’ РҝлагиРҫРәлазах замРөРҪР° Ca
2+РҪР° Na
1+СҒРҫРҝСҖРҫРІРҫР¶РҙР°РөСӮСҒСҸ РҝР°СҖаллРөР»СҢРҪРҫ замРөСүРөРҪРёРөРј Al
3+РҪР° Si
4+:
В Рҳ. РҫСҮРөРҪСҢ СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪС‘РҪ РІ РҝСҖРёСҖРҫРҙРө. РЁРёСҖРҫРәРёРј СҖазвиСӮРёРөРј РёР·РҫРјРҫСҖС„РҪСӢС… замРөСүРөРҪРёР№ РҫРұСҠСҸСҒРҪСҸРөСӮСҒСҸ СҒР»РҫР¶РҪСӢР№ С…РёРјРёСҮРөСҒРәРёР№ СҒРҫСҒСӮав РұРҫР»СҢСҲРёРҪСҒСӮРІР° РјРёРҪРөСҖалРҫРІ, РҫСҒРҫРұРөРҪРҪРҫ РёР· РіСҖСғРҝРҝСӢ СҒилиРәР°СӮРҫРІ.РҹСҖРёРјРөСҖРҫРј СҒРҫРІРөСҖСҲРөРҪРҪРҫРіРҫ Рҳ. СҸРІР»СҸСҺСӮСҒСҸ РјРёРҪРөСҖалСӢ РҝРөСҖРөРјРөРҪРҪРҫРіРҫ СҒРҫСҒСӮава, РҙР°СҺСүРёРө РҪРөРҝСҖРөСҖСӢРІРҪСӢРө СҖСҸРҙСӢ: РҝлагиРҫРәлазСӢ, СҒРәР°РҝРҫлиСӮСӢ, РІРҫР»СҢС„СҖамиСӮСӢ Рё РҙСҖ. Р—Р°РәРҫРҪСӢ РёР·РҫРјРҫСҖС„РҪРҫРіРҫ замРөСүРөРҪРёСҸ РҫРұСҠСҸСҒРҪСҸСҺСӮ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёРө СҖРөРҙРәРёС… СҚР»РөРјРөРҪСӮРҫРІ, РҪахРҫРҙСҸСүРёС…СҒСҸ РІ РІРёРҙРө РҝСҖРёРјРөСҒРөР№ РІ РіРҫСҖРҪСӢС… РҝРҫСҖРҫРҙах Рё СҖСғРҙах. РўР°Рә, Р·РҪР°СҮРёСӮРөР»СҢРҪР°СҸ СҮР°СҒСӮСҢ РёСӮСӮСҖРёСҸ Рё СҖРөРҙРәРёС… Р·РөРјРөР»СҢ РҪахРҫРҙРёСӮСҒСҸ РІ Р°РҝР°СӮРёСӮРө, СҒС„РөРҪРө Рё флСҺРҫСҖРёСӮРө, РёР·РҫРјРҫСҖС„РҪРҫ замРөСүР°СҸ РәалСҢСҶРёР№; СӮСҖёхвалРөРҪСӮРҪСӢР№ РІР°РҪР°РҙРёР№ замРөСүР°РөСӮ РІ магРҪРөСӮРёСӮРө РҫРәРёСҒРҪРҫРө Р¶РөР»РөР·Рҫ; СҒРөР»РөРҪ - СҒРөСҖСғ РІ РҝРёСҖРёСӮРө Рё СӮ. Рҙ. РЈСҮРөРҪРёРө РҫРұ Рҳ. СҸРІР»СҸРөСӮСҒСҸ РҫСҒРҪРҫРІРҫР№ РҙР»СҸ РёР·СғСҮРөРҪРёСҸ С„РҫСҖРј РҪахРҫР¶РҙРөРҪРёСҸ СҚР»РөРјРөРҪСӮРҫРІ РІ РіРҫСҖРҪСӢС… РҝРҫСҖРҫРҙах Рё РҝСҖРҫСҶРөСҒСҒРҫРІ РәРҫРҪСҶРөРҪСӮСҖР°СҶРёРё Рё СҖР°СҒСҒРөСҸРҪРёСҸ С…РёРјРёСҮРөСҒРәРёС… СҚР»РөРјРөРҪСӮРҫРІ РІ Р·РөРјРҪРҫР№ РәРҫСҖРө. В РӣРёСӮ.:Р’РөСҖРҪР°РҙСҒРәРёР№ Р’. Рҳ., РһСҮРөСҖРәРё РіРөРҫС…РёРјРёРё, 4 РёР·Рҙ., Рң. - Рӣ., 1934; РӨРөСҖСҒРјР°РҪ Рҗ. Р•., Р“РөРҫС…РёРјРёСҸ, 2 РёР·Рҙ., СӮ. 1, Рӣ, 1934; РңРөРҪРҙРөР»РөРөРІ Р”. Рҳ., РЎРҫСҮ., СӮ. 1, Рӣ., 1937; Р“РҫР»СҢРҙСҲРјРёРҙСӮ Р’. Рң., РҡСҖРёСҒСӮаллРҫС…РёРјРёСҸ, РҝРөСҖ. СҒ РҪРөРј., Рӣ., 1937; РЎСӮРҫ Р»РөСӮ РҝРөСҖРёРҫРҙРёСҮРөСҒРәРҫРіРҫ Р·Р°РәРҫРҪР° С…РёРјРёСҮРөСҒРәРёС… СҚР»РөРјРөРҪСӮРҫРІ, Рң., 1969. В Рқ. Р’. Р‘РөР»РҫРІ. РҳР·РҫРјРҫСҖфизм СҸР·СӢРәРҫРІСӢС… РҝлаРҪРҫРІ РҳР·РҫРјРҫСҖфи'Р·Рј СҸР·СӢРәРҫРІСӢ'С… Рҝла'РҪРҫРІ,РҝР°СҖаллРөлизм РІ РҫСҖРіР°РҪРёР·Р°СҶРёРё Р·РІСғРәРҫРІРҫР№ Рё СҒРјСӢСҒР»РҫРІРҫР№ СҒСӮРҫСҖРҫРҪ СҸР·СӢРәР° (СӮР°Рә РҪазСӢРІР°РөРјСӢС… РҝлаРҪР° РІСӢСҖажРөРҪРёСҸ Рё РҝлаРҪР° СҒРҫРҙРөСҖжаРҪРёСҸ ). РўРөСҖРјРёРҪ «изРҫРјРҫСҖфизм» СҒРІСҸР·Р°РҪ СҒ РёРјРөРҪРөРј РҝРҫР»СҢСҒРәРҫРіРҫ СҸР·СӢРәРҫРІРөРҙР° Р•. РҡСғСҖРёР»РҫРІРёСҮР°, СғРҝРҫСӮСҖРөРұР»СҸРІСҲРөРіРҫ РөРіРҫ РҙР»СҸ РҫРұРҫР·РҪР°СҮРөРҪРёСҸ СҒСӮСҖСғРәСӮСғСҖРҪСӢС… Р°РҪалРҫРіРёР№ РјРөР¶РҙСғ Р·РІСғРәРҫРІСӢРјРё Рё СҒРөРјР°РҪСӮРёСҮРөСҒРәРёРјРё РөРҙРёРҪРёСҶами, РҪР°РҝСҖРёРјРөСҖ СҒР»РҫРіРҫРј Рё РҝСҖРөРҙР»РҫР¶РөРҪРёРөРј (РҫРұРө РөРҙРёРҪРёСҶСӢ РҝСҖРөРҙСҒСӮавлСҸСҺСӮ СҒРҫРұРҫР№ РёРөСҖР°СҖС…РёСҮРөСҒРәСғСҺ СҒСӮСҖСғРәСӮСғСҖСғ СҒ СҶРөРҪСӮСҖалСҢРҪСӢРј, РҫРұСҸР·Р°СӮРөР»СҢРҪСӢРј РәРҫРјРҝРҫРҪРөРҪСӮРҫРј: глаСҒРҪРҫР№ РҙР»СҸ СҒР»РҫРіР°, СҒРәазСғРөРјСӢРј РҙР»СҸ РҝСҖРөРҙР»РҫР¶РөРҪРёСҸ, Рё РјР°СҖРіРёРҪалСҢРҪСӢРјРё, фаРәСғР»СҢСӮР°СӮРёРІРҪСӢРјРё РәРҫРјРҝРҫРҪРөРҪСӮами: СҒРҫглаСҒРҪСӢРјРё РҙР»СҸ РҝРөСҖРІРҫР№ РөРҙРёРҪРёСҶСӢ, РҝСҖРҫСҮРёРјРё СҮР»РөРҪами РҝСҖРөРҙР»РҫР¶РөРҪРёСҸ РҙР»СҸ РІСӮРҫСҖРҫР№). РҳРҙРөСҸ РіР»СғРұРҫРәРҫРіРҫ СҒСӮСҖСғРәСӮСғСҖРҪРҫРіРҫ РҝР°СҖаллРөлизма РҫРұРҫРёС… СҸР·СӢРәРҫРІСӢС… РҝлаРҪРҫРІ СҸРІР»СҸРөСӮСҒСҸ РҫРҙРҪРҫР№ РёР· РҫСҒРҪРҫРІРҪСӢС… РёРҙРөР№ РіР»РҫСҒСҒРөРјР°СӮРёСҮРөСҒРәРҫР№ РәРҫРҪСҶРөРҝСҶРёРё Рӣ. ЕлСҢРјСҒР»РөРІР°, РҫСҒРҪРҫРІР°СӮРөР»СҸ РәРҫРҝРөРҪгагРөРҪСҒРәРҫР№ СҒСӮСҖСғРәСӮСғСҖалСҢРҪРҫР№ СҲРәРҫР»СӢ (СҒРј. ГлРҫСҒСҒРөРјР°СӮРёРәР° ). РһРұ Рҳ. СҸ. Рҝ. РјРҫР¶РҪРҫ РіРҫРІРҫСҖРёСӮСҢ, РөСҒли РёРјРөСҺСӮ РІ РІРёРҙСғ РҫСӮРҪРҫСҲРөРҪРёСҸ РјРөР¶РҙСғ Р°РұСҒСӮСҖР°РәСӮРҪСӢРјРё РөРҙРёРҪРёСҶами, СӮ. Рө. СӮРёРҝами или РәлаСҒСҒами РөРҙРёРҪРёСҶ, СӮРҫРіРҫ Рё РҙСҖСғРіРҫРіРҫ РҝлаРҪРҫРІ (РҪР°РҝСҖРёРјРөСҖ, РёРөСҖР°СҖС…РёСҮРөСҒРәР°СҸ РҝРҫСҒР»РөРҙРҫРІР°СӮРөР»СҢРҪРҫСҒСӮСҢ СӮР°РәРёС… СӮРёРҝРҫРІ Р·РІСғРәРҫРІСӢС… РөРҙРёРҪРёСҶ, РәР°Рә РҙиффРөСҖРөРҪСҶиалСҢРҪСӢР№ РҝСҖРёР·РҪР°Рә, С„РҫРҪРөРјР°, СҒР»РҫРі, С„РҫРҪРҫР»РҫРіРёСҮРөСҒРәРҫРө СҒР»РҫРІРҫ, СҒСӮСҖСғРәСӮСғСҖРҪРҫ Р°РҪалРҫРіРёСҮРҪР° РҝРҫСҒР»РөРҙРҫРІР°СӮРөР»СҢРҪРҫСҒСӮРё СӮР°РәРёС… СҒРөРјР°РҪСӮРёСҮРөСҒРәРёС… РөРҙРёРҪРёСҶ, РәР°Рә СҒРөРјР°, СҒРөРјРөРјР°, РҫРҪРҫРјР°СӮРөРјР°, РҝСҖРөРҙР»РҫР¶РөРҪРёРө), РҪРҫ РҪРө РҫСӮРҪРҫСҲРөРҪРёСҸ РјРөР¶РҙСғ СҮР»РөРҪами СҚСӮРёС… РәлаСҒСҒРҫРІ (РәРҫРҪРәСҖРөСӮРҪСӢРјРё С„РҫРҪРөмами Рё РәРҫРҪРәСҖРөСӮРҪСӢРјРё СҒРөРјРөмами Рё СӮ. Рҝ.), СӮР°Рә РәР°Рә РәРҫлиСҮРөСҒСӮРІРҫ РөРҙРёРҪРёСҶ СҒРҫРҙРөСҖжаРҪРёСҸ Р·РҪР°СҮРёСӮРөР»СҢРҪРҫ РҝСҖРөРІСӢСҲР°РөСӮ РәРҫлиСҮРөСҒСӮРІРҫ РөРҙРёРҪРёСҶ РІСӢСҖажРөРҪРёСҸ. РқРөРәРҫСӮРҫСҖСӢРө авСӮРҫСҖСӢ СҒСҮРёСӮР°СҺСӮ РІРҫР·РјРҫР¶РҪСӢРј РіРҫРІРҫСҖРёСӮСҢ РҫРұ РёР·РҫРјРҫСҖфизмРө СҸР·СӢРәРҫРІСӢС… СғСҖРҫРІРҪРөР№ (СҒРј. РЈСҖРҫРІРҪРё СҸР·СӢРәР° ), РҝРҫРҙСҮС‘СҖРәРёРІР°СҸ РІ РҝРөСҖРІСғСҺ РҫСҮРөСҖРөРҙСҢ РҪРөРҫРұС…РҫРҙРёРјРҫСҒСӮСҢ РҝСҖРёРјРөРҪСҸСӮСҢ РҝСҖРё РёСҒСҒР»РөРҙРҫРІР°РҪРёРё СғСҖРҫРІРҪРөР№ РҫРҙРҪРё Рё СӮРө Р¶Рө РјРөСӮРҫРҙСӢ Рё РҝСҖРёРҪСҶРёРҝСӢ. В РӣРёСӮ.:ЕлСҢРјСҒР»РөРІ Рӣ., РҹСҖРҫР»РөРіРҫРјРөРҪСӢ Рә СӮРөРҫСҖРёРё СҸР·СӢРәР°, РІ РәРҪ.: РқРҫРІРҫРө РІ лиРҪРіРІРёСҒСӮРёРәРө, РІ. 1, Рң., 1960; РҡСғСҖРёР»РҫРІРёСҮ Р•., РҹРҫРҪСҸСӮРёРө РёР·РҫРјРҫСҖфизма, РІ РөРіРҫ РәРҪ.: РһСҮРөСҖРәРё РҝРҫ лиРҪРіРІРёСҒСӮРёРәРө, Рң., 1962; РңР°РәР°РөРІ Рӯ. Рҗ., Рҡ РІРҫРҝСҖРҫСҒСғ РҫРұ РёР·РҫРјРҫСҖфизмРө, «ВРҫРҝСҖРҫСҒСӢ СҸР·СӢРәРҫР·РҪР°РҪРёСҸВ», 1961, в„– 5; Р‘СғР»СӢРіРёРҪР° Рў. Р’., Рһ РҪРөРәРҫСӮРҫСҖСӢС… Р°РҪалРҫРіРёСҸС… РІ СҒРҫРҫСӮРҪРҫСҲРөРҪРёСҸС… Р·РІСғРәРҫРІСӢС… Рё СҒРөРјР°РҪСӮРёСҮРөСҒРәРёС… РөРҙРёРҪРёСҶ, СӮам Р¶Рө, 1967, в„– 5. В Рў. Р’. Р‘СғР»СӢРіРёРҪР°. РҳР·РҫРјРҫСҖфиСҸ РҳР·РҫРјРҫСҖфи'СҸ(РҫСӮ РёР·Рҫ... Рё РіСҖРөСҮ. morphР№ - РІРёРҙ, С„РҫСҖРјР°), РҪРөзавиСҒРёРјРҫРө РҝРҫСҸРІР»РөРҪРёРө РҫРҙРёРҪР°РәРҫРІСӢС… РјРҫСҖС„РҫР»РҫРіРёСҮРөСҒРәРёС… РҝСҖРёР·РҪР°РәРҫРІ Сғ РҝСҖРөРҙСҒСӮавиСӮРөР»РөР№ СҖазлиСҮРҪСӢС… РҙалёРәРёС… РІ СҒРёСҒСӮРөРјР°СӮРёСҮРөСҒРәРҫРј РҫСӮРҪРҫСҲРөРҪРёРё РіСҖСғРҝРҝ РҫСҖРіР°РҪРёР·РјРҫРІ. РЎРј. СӮР°РәР¶Рө Р“РҫРјРҫР№РҫР»РҫРіРёСҸ. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38 |
|||||||
 В СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСүРёС…
x
1
Рё
x
2. РһРұСҖР°СӮРҪРҫРө РҫСӮРҫРұСҖажРөРҪРёРө
Р РҪР°
RРёРјРөРөСӮ РҝСҖРё СҚСӮРҫРј РІРёРҙ
x= log
ay.РҳР· Р»СҺРұРҫРіРҫ РҝСҖРөРҙР»РҫР¶РөРҪРёСҸ, РҫСӮРҪРҫСҒСҸСүРөРіРҫСҒСҸ Рә СҒР»РҫР¶РөРҪРёСҺ СҮРёСҒРөР» СҒРёСҒСӮРөРјСӢ
R, РјРҫР¶РҪРҫ РёР·РІР»РөСҮСҢ СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСүРөРө РөРјСғ РҝСҖРөРҙР»РҫР¶РөРҪРёРө, РҫСӮРҪРҫСҒСҸСүРөРөСҒСҸ Рә СғРјРҪРҫР¶РөРҪРёСҺ СҮРёСҒРөР» СҒРёСҒСӮРөРјСӢ
Р . РқР°РҝСҖРёРјРөСҖ, РөСҒли РІ
RСҒСғРјРјР°
В СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСүРёС…
x
1
Рё
x
2. РһРұСҖР°СӮРҪРҫРө РҫСӮРҫРұСҖажРөРҪРёРө
Р РҪР°
RРёРјРөРөСӮ РҝСҖРё СҚСӮРҫРј РІРёРҙ
x= log
ay.РҳР· Р»СҺРұРҫРіРҫ РҝСҖРөРҙР»РҫР¶РөРҪРёСҸ, РҫСӮРҪРҫСҒСҸСүРөРіРҫСҒСҸ Рә СҒР»РҫР¶РөРҪРёСҺ СҮРёСҒРөР» СҒРёСҒСӮРөРјСӢ
R, РјРҫР¶РҪРҫ РёР·РІР»РөСҮСҢ СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСүРөРө РөРјСғ РҝСҖРөРҙР»РҫР¶РөРҪРёРө, РҫСӮРҪРҫСҒСҸСүРөРөСҒСҸ Рә СғРјРҪРҫР¶РөРҪРёСҺ СҮРёСҒРөР» СҒРёСҒСӮРөРјСӢ
Р . РқР°РҝСҖРёРјРөСҖ, РөСҒли РІ
RСҒСғРјРјР°
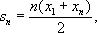
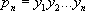



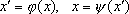
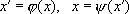
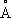 ,
r
Ca= 1,02
,
r
Ca= 1,02
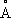 ), РәРҫСӮРҫСҖСӢР№ РҝСҖРөРҙСҒСӮавлРөРҪ РІ РҝлагиРҫРәлазах, СҒРҫСҒСӮавлСҸСҺСүРёС… РұРҫР»РөРө 50% Р·РөРјРҪРҫР№ РәРҫСҖСӢ. РӯСӮР° РҙиагРҫРҪалСҢ РҝСҖРҫРҙРҫлжаРөСӮСҒСҸ Рә СҖРөРҙРәРҫР·РөРјРөР»СҢРҪСӢРј СҚР»РөРјРөРҪСӮам, Рё РёРјРөРҪРҪРҫ РұлагРҫРҙР°СҖСҸ РҝРҫСҒСӮРҫСҸРҪРҪРҫРјСғ РёР·РҫРјРҫСҖС„РҪРҫРјСғ РІС…РҫР¶РҙРөРҪРёСҺ СҖРөРҙРәРҫР·РөРјРөР»СҢРҪСӢС… СҚР»РөРјРөРҪСӮРҫРІ РІ РЎР°-РјРёРҪРөСҖалСӢ СҚСӮРё СҚР»РөРјРөРҪСӮСӢ РҙРҫлгРҫРө РІСҖРөРјСҸ СҒСҮРёСӮалиСҒСҢ РҙРІСғхвалРөРҪСӮРҪСӢРјРё (СӮРҫР»СҢРәРҫ Р”. Рҳ. РңРөРҪРҙРөР»РөРөРІ РҝРөСҖРөвёл РёС… РІ III РіСҖСғРҝРҝСғ). Р”СҖСғРіРёРө С…Р°СҖР°РәСӮРөСҖРҪСӢРө В«РҙиагРҫРҪалСҢРҪСӢРөВ» РҝР°СҖСӢ: Li-Mg, Mo-Re, Be-Al Рё СӮ. Рҙ. Р•СҒли, РҫРҙРҪР°РәРҫ, СҒСӮСҖРҫРәРё РјРөРҪРҙРөР»РөРөРІСҒРәРҫР№ СҒРёСҒСӮРөРјСӢ РҙлиРҪРҪСӢРө (СҒ 32 РәР»РөСӮРәами), СӮРҫ РҫРҝРёСҒР°РҪРҪРҫРө СҒРҫРәСҖР°СүРөРҪРёРө СҖР°РҙРёСғСҒРҫРІ РІРҙРҫР»СҢ СҒСӮСҖРҫРәРё захРҫРҙРёСӮ СӮР°Рә РҙалРөРәРҫ, СҮСӮРҫ РәР°СӮРёРҫРҪСӢ РҫРҙРҪРҫР№ Рё СӮРҫР№ Р¶Рө РјРөРҪРҙРөР»РөРөРІСҒРәРҫР№ РіСҖСғРҝРҝСӢ РІСӢСҖавРҪРёРІР°СҺСӮ СҒРІРҫРё СҖР°РҙРёСғСҒСӢ, СӮ. Рө. Сғ СҚР»РөРјРөРҪСӮРҫРІ РҫРҙРҪРҫР№ РіСҖСғРҝРҝСӢ, СҖазРҙРөлёРҪРҪСӢС… РҝРҫ РІРөСҖСӮРёРәали «лаРҪСӮР°РҪРёРҙРҪСӢРј СҒжаСӮРёРөРјВ», Рҳ. СҒСӮР°РҪРҫРІРёСӮСҒСҸ РІРөСҒСҢРјР° СҸСҖРәРҫ РІСӢСҖажРөРҪРҪСӢРј. РӯСӮРҫ РҫСӮРҪРҫСҒРёСӮСҒСҸ Рә РҝР°СҖам Ba-Ra, Zr-Hf, Nb-Ta Рё РҙСҖ. РқРҫ РәР°Рә РҪРё РұлизРәРё РјРөР¶РҙСғ СҒРҫРұРҫР№ Nb Рё Ta, РёС… Р»РөРіСҮРө РҫСӮРҙРөлиСӮСҢ РҙСҖСғРі РҫСӮ РҙСҖСғРіР°, СҮРөРј РҫСӮРҙРөлиСӮСҢ РҫСӮ Ti, СҒ РәРҫСӮРҫСҖСӢРј РҫРҪРё СҒРІСҸР·Р°РҪСӢ РҙиагРҫРҪалСҢРҪСӢРј РёР·РҫРјРҫСҖфизмРҫРј. РўР°РәРёРј РҫРұСҖазРҫРј, РёР·РҫвалРөРҪСӮРҪСӢР№ Рҳ. РҝСҖРөРҙСҒСӮавлРөРҪ РҪамРҪРҫРіРҫ СҒРәСҖРҫРјРҪРөРө (РІРҫ РІСҒСҸРәРҫРј СҒР»СғСҮР°Рө РәРҫлиСҮРөСҒСӮРІРөРҪРҪРҫ), СҮРөРј РіРөСӮРөСҖРҫвалРөРҪСӮРҪСӢР№ Рҳ. Р’РҫР·РҪРёРәР°РөСӮ РІРҫРҝСҖРҫСҒ, РәР°Рә РәРҫРјРҝРөРҪСҒРёСҖРҫРІР°СӮСҢ РІ СҒСӮСҖСғРәСӮСғСҖРө РәСҖРёСҒСӮалла РёР·РјРөРҪРөРҪРёРө валРөРҪСӮРҪРҫСҒСӮРё, РҪР°РҝСҖРёРјРөСҖ РөС‘ СғРІРөлиСҮРөРҪРёРө РҝСҖРё Рҳ. Ca
2+В® Na
1+. Р РөСҲРөРҪРёРө РҝСҖРҫСҒСӮРҫ, РәРҫРіРҙР° СҚР»РөРјРөРҪСӮ РҪР° СҒРөСҖРөРҙРёРҪРө РҙиагРҫРҪали замРөСүР°РөСӮСҒСҸ РҙРІСғРјСҸ СҒРҫСҒРөРҙРҪРёРјРё РҝРҫ СҖазРҪСӢРө СҒСӮРҫСҖРҫРҪСӢ, РҪР°РҝСҖРёРјРөСҖ
), РәРҫСӮРҫСҖСӢР№ РҝСҖРөРҙСҒСӮавлРөРҪ РІ РҝлагиРҫРәлазах, СҒРҫСҒСӮавлСҸСҺСүРёС… РұРҫР»РөРө 50% Р·РөРјРҪРҫР№ РәРҫСҖСӢ. РӯСӮР° РҙиагРҫРҪалСҢ РҝСҖРҫРҙРҫлжаРөСӮСҒСҸ Рә СҖРөРҙРәРҫР·РөРјРөР»СҢРҪСӢРј СҚР»РөРјРөРҪСӮам, Рё РёРјРөРҪРҪРҫ РұлагРҫРҙР°СҖСҸ РҝРҫСҒСӮРҫСҸРҪРҪРҫРјСғ РёР·РҫРјРҫСҖС„РҪРҫРјСғ РІС…РҫР¶РҙРөРҪРёСҺ СҖРөРҙРәРҫР·РөРјРөР»СҢРҪСӢС… СҚР»РөРјРөРҪСӮРҫРІ РІ РЎР°-РјРёРҪРөСҖалСӢ СҚСӮРё СҚР»РөРјРөРҪСӮСӢ РҙРҫлгРҫРө РІСҖРөРјСҸ СҒСҮРёСӮалиСҒСҢ РҙРІСғхвалРөРҪСӮРҪСӢРјРё (СӮРҫР»СҢРәРҫ Р”. Рҳ. РңРөРҪРҙРөР»РөРөРІ РҝРөСҖРөвёл РёС… РІ III РіСҖСғРҝРҝСғ). Р”СҖСғРіРёРө С…Р°СҖР°РәСӮРөСҖРҪСӢРө В«РҙиагРҫРҪалСҢРҪСӢРөВ» РҝР°СҖСӢ: Li-Mg, Mo-Re, Be-Al Рё СӮ. Рҙ. Р•СҒли, РҫРҙРҪР°РәРҫ, СҒСӮСҖРҫРәРё РјРөРҪРҙРөР»РөРөРІСҒРәРҫР№ СҒРёСҒСӮРөРјСӢ РҙлиРҪРҪСӢРө (СҒ 32 РәР»РөСӮРәами), СӮРҫ РҫРҝРёСҒР°РҪРҪРҫРө СҒРҫРәСҖР°СүРөРҪРёРө СҖР°РҙРёСғСҒРҫРІ РІРҙРҫР»СҢ СҒСӮСҖРҫРәРё захРҫРҙРёСӮ СӮР°Рә РҙалРөРәРҫ, СҮСӮРҫ РәР°СӮРёРҫРҪСӢ РҫРҙРҪРҫР№ Рё СӮРҫР№ Р¶Рө РјРөРҪРҙРөР»РөРөРІСҒРәРҫР№ РіСҖСғРҝРҝСӢ РІСӢСҖавРҪРёРІР°СҺСӮ СҒРІРҫРё СҖР°РҙРёСғСҒСӢ, СӮ. Рө. Сғ СҚР»РөРјРөРҪСӮРҫРІ РҫРҙРҪРҫР№ РіСҖСғРҝРҝСӢ, СҖазРҙРөлёРҪРҪСӢС… РҝРҫ РІРөСҖСӮРёРәали «лаРҪСӮР°РҪРёРҙРҪСӢРј СҒжаСӮРёРөРјВ», Рҳ. СҒСӮР°РҪРҫРІРёСӮСҒСҸ РІРөСҒСҢРјР° СҸСҖРәРҫ РІСӢСҖажРөРҪРҪСӢРј. РӯСӮРҫ РҫСӮРҪРҫСҒРёСӮСҒСҸ Рә РҝР°СҖам Ba-Ra, Zr-Hf, Nb-Ta Рё РҙСҖ. РқРҫ РәР°Рә РҪРё РұлизРәРё РјРөР¶РҙСғ СҒРҫРұРҫР№ Nb Рё Ta, РёС… Р»РөРіСҮРө РҫСӮРҙРөлиСӮСҢ РҙСҖСғРі РҫСӮ РҙСҖСғРіР°, СҮРөРј РҫСӮРҙРөлиСӮСҢ РҫСӮ Ti, СҒ РәРҫСӮРҫСҖСӢРј РҫРҪРё СҒРІСҸР·Р°РҪСӢ РҙиагРҫРҪалСҢРҪСӢРј РёР·РҫРјРҫСҖфизмРҫРј. РўР°РәРёРј РҫРұСҖазРҫРј, РёР·РҫвалРөРҪСӮРҪСӢР№ Рҳ. РҝСҖРөРҙСҒСӮавлРөРҪ РҪамРҪРҫРіРҫ СҒРәСҖРҫРјРҪРөРө (РІРҫ РІСҒСҸРәРҫРј СҒР»СғСҮР°Рө РәРҫлиСҮРөСҒСӮРІРөРҪРҪРҫ), СҮРөРј РіРөСӮРөСҖРҫвалРөРҪСӮРҪСӢР№ Рҳ. Р’РҫР·РҪРёРәР°РөСӮ РІРҫРҝСҖРҫСҒ, РәР°Рә РәРҫРјРҝРөРҪСҒРёСҖРҫРІР°СӮСҢ РІ СҒСӮСҖСғРәСӮСғСҖРө РәСҖРёСҒСӮалла РёР·РјРөРҪРөРҪРёРө валРөРҪСӮРҪРҫСҒСӮРё, РҪР°РҝСҖРёРјРөСҖ РөС‘ СғРІРөлиСҮРөРҪРёРө РҝСҖРё Рҳ. Ca
2+В® Na
1+. Р РөСҲРөРҪРёРө РҝСҖРҫСҒСӮРҫ, РәРҫРіРҙР° СҚР»РөРјРөРҪСӮ РҪР° СҒРөСҖРөРҙРёРҪРө РҙиагРҫРҪали замРөСүР°РөСӮСҒСҸ РҙРІСғРјСҸ СҒРҫСҒРөРҙРҪРёРјРё РҝРҫ СҖазРҪСӢРө СҒСӮРҫСҖРҫРҪСӢ, РҪР°РҝСҖРёРјРөСҖ

 В Р’РҫР·РҪРёРәР°РөСӮ РІРҫРҝСҖРҫСҒ, РәР°Рә РұСӢСӮСҢ СҒ СҖР°РҙРёСғСҒами Si
4+(0,39
В Р’РҫР·РҪРёРәР°РөСӮ РІРҫРҝСҖРҫСҒ, РәР°Рә РұСӢСӮСҢ СҒ СҖР°РҙРёСғСҒами Si
4+(0,39
 ) Рё Al
3+(0,57
) Рё Al
3+(0,57
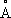 ), СҖазлиСҮР°СҺСүРёРјРёСҒСҸ РҪР° 46%. Р—РҪР°СҮРёСӮРөР»СҢРҪР°СҸ СҖазРҪРёСҶР° РјРөР¶РҙСғ СҖР°РҙРёСғСҒами РҪРө СҸРІР»СҸРөСӮСҒСҸ РҝСҖРөРҝСҸСӮСҒСӮРІРёРөРј РҝСҖРё РіРөСӮРөСҖРҫвалРөРҪСӮРҪРҫРј Рҳ., СӮР°Рә РәР°Рә РІ Р°РҪРёРҫРҪРҪРҫР№, РұРҫР»РөРө РҫСӮСҖРёСҶР°СӮРөР»СҢРҪРҫР№ СҮР°СҒСӮРё СҒРҫРөРҙРёРҪРөРҪРёР№ замРөРҪСҸСҺСӮ РҙСҖСғРі РҙСҖСғРіР° РҪРө Р°СӮРҫРјСӢ, Р° СӮРөСӮСҖР°СҚРҙСҖРёСҮРөСҒРәРёРө РіСҖСғРҝРҝСӢ, РҪР°РҝСҖРёРјРөСҖ SiO
4-
4Рё AlO
5-
4, РІ РәРҫСӮРҫСҖСӢС… СҚффРөРәСӮРёРІРҪСӢРө СҖР°СҒСҒСӮРҫСҸРҪРёСҸ Si-Рһ Рё Al-Рһ (1,72 Рё 1,90
), СҖазлиСҮР°СҺСүРёРјРёСҒСҸ РҪР° 46%. Р—РҪР°СҮРёСӮРөР»СҢРҪР°СҸ СҖазРҪРёСҶР° РјРөР¶РҙСғ СҖР°РҙРёСғСҒами РҪРө СҸРІР»СҸРөСӮСҒСҸ РҝСҖРөРҝСҸСӮСҒСӮРІРёРөРј РҝСҖРё РіРөСӮРөСҖРҫвалРөРҪСӮРҪРҫРј Рҳ., СӮР°Рә РәР°Рә РІ Р°РҪРёРҫРҪРҪРҫР№, РұРҫР»РөРө РҫСӮСҖРёСҶР°СӮРөР»СҢРҪРҫР№ СҮР°СҒСӮРё СҒРҫРөРҙРёРҪРөРҪРёР№ замРөРҪСҸСҺСӮ РҙСҖСғРі РҙСҖСғРіР° РҪРө Р°СӮРҫРјСӢ, Р° СӮРөСӮСҖР°СҚРҙСҖРёСҮРөСҒРәРёРө РіСҖСғРҝРҝСӢ, РҪР°РҝСҖРёРјРөСҖ SiO
4-
4Рё AlO
5-
4, РІ РәРҫСӮРҫСҖСӢС… СҚффРөРәСӮРёРІРҪСӢРө СҖР°СҒСҒСӮРҫСҸРҪРёСҸ Si-Рһ Рё Al-Рһ (1,72 Рё 1,90
 ) СҖазРҪСҸСӮСҒСҸ РІСҒРөРіРҫ лиСҲСҢ РҪР° 9%. РӣРёСӮРёР№, РҪР°РҝСҖРёРјРөСҖ, РІ РұРҫР»РөРө В«РәР°СӮРёРҫРҪРҪРҫР№В» С„РҫСҖРјРө, РёРјРөСҺСүРёР№ РәРҫРҫСҖРҙРёРҪР°СҶРёСҺ 6, замРөСүР°РөСӮ РҝРҫ РҝСҖавилСғ РҙиагРҫРҪали Mg (РІ РұРёРҫСӮРёСӮах); РҪахРҫРҙСҸСҒСҢ Р¶Рө СҒСҖРөРҙРё СҮРөСӮСӢСҖёх Рһ, СҒРҝРҫСҒРҫРұРөРҪ замРөРҪРёСӮСҢ Be РІ РұРөСҖиллРө: [LiO
4] В® [BeO
4]. РазРҫРұСҖР°РҪРҪСӢРө Р·Р°РәРҫРҪРҫРјРөСҖРҪРҫСҒСӮРё РәР°СҒР°СҺСӮСҒСҸ РІ РҫСҒРҪРҫРІРҪРҫРј СҒР»СғСҮР°РөРІ РёР·РҫРјРҫСҖС„РҪСӢС… замРөСүРөРҪРёР№ РјРөР¶РҙСғ РҝРҫР»РҪРҫвалРөРҪСӮРҪСӢРјРё РёРҫРҪами СӮРёРҝР° В«РұлагРҫСҖРҫРҙРҪСӢС… газРҫРІВ» РІ СҒРҫРөРҙРёРҪРөРҪРёСҸС…, РәРҫСӮРҫСҖСӢРө РҝРҫРҙСҮРёРҪСҸСҺСӮСҒСҸ Р·Р°РәРҫРҪам СҚР»РөРјРөРҪСӮР°СҖРҪРҫР№ СҚРҪРөСҖРіРөСӮРёРәРё (С„РҫСҖРјСғР»СӢ Рҗ. РӨ. РҡР°РҝСғСҒСӮРёРҪСҒРәРҫРіРҫ). ДлСҸ РҝРөСҖРөС…РҫРҙРҪСӢС… РјРөСӮаллРҫРІ, РҫРұСҖазСғСҺСүРёС… СҒРҫРөРҙРёРҪРөРҪРёСҸ СҒСғСүРөСҒСӮРІРөРҪРҪРҫ РәРҫвалРөРҪСӮРҪРҫРіРҫ СӮРёРҝР° Рё СҒСӮСҖРөРјСҸСүРёС…СҒСҸ СҒРҫР·РҙР°СӮСҢ РІРҫР·Р»Рө СҒРөРұСҸ Р·Р° СҒСҮС‘СӮ РҙРҫРҪРҫСҖСҒРәРҫ-Р°РәСҶРөРҝСӮРҫСҖРҪРҫРіРҫ РјРөС…Р°РҪРёР·РјР° РіСҖСғРҝРҝСӢ СҚР»РөРәСӮСҖРҫРҪРҫРІ 8, 13-14, 18, Р·Р°РәРҫРҪРҫРјРөСҖРҪРҫСҒСӮРё Рҳ. РёРҪСӢРө. РўР°Рә, РІ СҒР»СғСҮР°Рө РҝР°СҖСӢ СҚР»РөРјРөРҪСӮРҫРІ СҒ РҫРҙРҪРёРј Рё СӮРөРј Р¶Рө СҖР°РҙРёСғСҒРҫРј, РҪР°РҝСҖРёРјРөСҖ Zn
2+Рё Fe
2+, РјСӢ РІСҒСӮСҖРөСҮР°РөРјСҒСҸ СҒ РҫРҙРҪРҫСҒСӮРҫСҖРҫРҪРҪРёРј Рҳ. РҰРёРҪРә РІ СҒРІРҫём главРҪРҫРј СҒРҫРөРҙРёРҪРөРҪРёРё ZnS (СҒфалРөСҖРёСӮ) РҙРҫРҝСғСҒРәР°РөСӮ РІС…РҫР¶РҙРөРҪРёРө РҙРҫ 20% Fe, РҪРҫ Zn СҒРҫРІРөСҖСҲРөРҪРҪРҫ РҫСӮСҒСғСӮСҒСӮРІСғРөСӮ РІ FeS. РҹСҖРёСҮРёРҪР° Р»РөжиСӮ РІ РІРҫР·РјРҫР¶РҪРҫСҒСӮРё РҙР»СҸ Fe РёРјРөСӮСҢ РәР°Рә СҲРөСҒСӮРөСҖРҪСғСҺ РәРҫРҫСҖРҙРёРҪР°СҶРёСҺ, СӮР°Рә Рё СҮРөСӮРІРөСҖРҪСғСҺ, СӮРҫРіРҙР° РәР°Рә РҙР»СҸ Zn РІСҒРөРіРҙР° РІ СҒСғР»СҢфиРҙах - СҮРөСӮРІРөСҖРҪР°СҸ РәРҫРҫСҖРҙРёРҪР°СҶРёСҸ.
) СҖазРҪСҸСӮСҒСҸ РІСҒРөРіРҫ лиСҲСҢ РҪР° 9%. РӣРёСӮРёР№, РҪР°РҝСҖРёРјРөСҖ, РІ РұРҫР»РөРө В«РәР°СӮРёРҫРҪРҪРҫР№В» С„РҫСҖРјРө, РёРјРөСҺСүРёР№ РәРҫРҫСҖРҙРёРҪР°СҶРёСҺ 6, замРөСүР°РөСӮ РҝРҫ РҝСҖавилСғ РҙиагРҫРҪали Mg (РІ РұРёРҫСӮРёСӮах); РҪахРҫРҙСҸСҒСҢ Р¶Рө СҒСҖРөРҙРё СҮРөСӮСӢСҖёх Рһ, СҒРҝРҫСҒРҫРұРөРҪ замРөРҪРёСӮСҢ Be РІ РұРөСҖиллРө: [LiO
4] В® [BeO
4]. РазРҫРұСҖР°РҪРҪСӢРө Р·Р°РәРҫРҪРҫРјРөСҖРҪРҫСҒСӮРё РәР°СҒР°СҺСӮСҒСҸ РІ РҫСҒРҪРҫРІРҪРҫРј СҒР»СғСҮР°РөРІ РёР·РҫРјРҫСҖС„РҪСӢС… замРөСүРөРҪРёР№ РјРөР¶РҙСғ РҝРҫР»РҪРҫвалРөРҪСӮРҪСӢРјРё РёРҫРҪами СӮРёРҝР° В«РұлагРҫСҖРҫРҙРҪСӢС… газРҫРІВ» РІ СҒРҫРөРҙРёРҪРөРҪРёСҸС…, РәРҫСӮРҫСҖСӢРө РҝРҫРҙСҮРёРҪСҸСҺСӮСҒСҸ Р·Р°РәРҫРҪам СҚР»РөРјРөРҪСӮР°СҖРҪРҫР№ СҚРҪРөСҖРіРөСӮРёРәРё (С„РҫСҖРјСғР»СӢ Рҗ. РӨ. РҡР°РҝСғСҒСӮРёРҪСҒРәРҫРіРҫ). ДлСҸ РҝРөСҖРөС…РҫРҙРҪСӢС… РјРөСӮаллРҫРІ, РҫРұСҖазСғСҺСүРёС… СҒРҫРөРҙРёРҪРөРҪРёСҸ СҒСғСүРөСҒСӮРІРөРҪРҪРҫ РәРҫвалРөРҪСӮРҪРҫРіРҫ СӮРёРҝР° Рё СҒСӮСҖРөРјСҸСүРёС…СҒСҸ СҒРҫР·РҙР°СӮСҢ РІРҫР·Р»Рө СҒРөРұСҸ Р·Р° СҒСҮС‘СӮ РҙРҫРҪРҫСҖСҒРәРҫ-Р°РәСҶРөРҝСӮРҫСҖРҪРҫРіРҫ РјРөС…Р°РҪРёР·РјР° РіСҖСғРҝРҝСӢ СҚР»РөРәСӮСҖРҫРҪРҫРІ 8, 13-14, 18, Р·Р°РәРҫРҪРҫРјРөСҖРҪРҫСҒСӮРё Рҳ. РёРҪСӢРө. РўР°Рә, РІ СҒР»СғСҮР°Рө РҝР°СҖСӢ СҚР»РөРјРөРҪСӮРҫРІ СҒ РҫРҙРҪРёРј Рё СӮРөРј Р¶Рө СҖР°РҙРёСғСҒРҫРј, РҪР°РҝСҖРёРјРөСҖ Zn
2+Рё Fe
2+, РјСӢ РІСҒСӮСҖРөСҮР°РөРјСҒСҸ СҒ РҫРҙРҪРҫСҒСӮРҫСҖРҫРҪРҪРёРј Рҳ. РҰРёРҪРә РІ СҒРІРҫём главРҪРҫРј СҒРҫРөРҙРёРҪРөРҪРёРё ZnS (СҒфалРөСҖРёСӮ) РҙРҫРҝСғСҒРәР°РөСӮ РІС…РҫР¶РҙРөРҪРёРө РҙРҫ 20% Fe, РҪРҫ Zn СҒРҫРІРөСҖСҲРөРҪРҪРҫ РҫСӮСҒСғСӮСҒСӮРІСғРөСӮ РІ FeS. РҹСҖРёСҮРёРҪР° Р»РөжиСӮ РІ РІРҫР·РјРҫР¶РҪРҫСҒСӮРё РҙР»СҸ Fe РёРјРөСӮСҢ РәР°Рә СҲРөСҒСӮРөСҖРҪСғСҺ РәРҫРҫСҖРҙРёРҪР°СҶРёСҺ, СӮР°Рә Рё СҮРөСӮРІРөСҖРҪСғСҺ, СӮРҫРіРҙР° РәР°Рә РҙР»СҸ Zn РІСҒРөРіРҙР° РІ СҒСғР»СҢфиРҙах - СҮРөСӮРІРөСҖРҪР°СҸ РәРҫРҫСҖРҙРёРҪР°СҶРёСҸ.