 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ИЗ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ИЗ) - Чтение (стр. 16)
В РҹСҖРҫСҒСӮРөР№СҲРёРј Рё РёСҒСӮРҫСҖРёСҮРөСҒРәРё РҝРөСҖРІСӢРј РёР·РІРөСҒСӮРҪСӢРј РІРёРҙРҫРј Рҳ. СҸРІР»СҸРөСӮСҒСҸ РҝСҖСҸРјРҫРө Рҳ., РҝСҖРё РәРҫСӮРҫСҖРҫРј СҖРөР·СғР»СҢСӮР°СӮ РҝРҫР»СғСҮР°РөСӮСҒСҸ РҪРөРҝРҫСҒСҖРөРҙСҒСӮРІРөРҪРҪРҫ РёР· Рҳ. СҒамРҫР№ РІРөлиСҮРёРҪСӢ (РҪР°РҝСҖРёРјРөСҖ, Рҳ. РҙлиРҪСӢ РҝСҖРҫРіСҖР°РҙСғРёСҖРҫРІР°РҪРҪРҫР№ лиРҪРөР№РәРҫР№, Рҳ. РјР°СҒСҒСӢ СӮРөла РҝСҖРё РҝРҫРјРҫСүРё РіРёСҖСҢ Рё СӮ. Рҙ.). РһРҙРҪР°РәРҫ РҝСҖСҸРјСӢРө Рҳ. РҪРө РІСҒРөРіРҙР° РІРҫР·РјРҫР¶РҪСӢ. Р’ СҚСӮРёС… СҒР»СғСҮР°СҸС… РҝСҖРёРұРөРіР°СҺСӮ Рә РәРҫСҒРІРөРҪРҪСӢРј Рҳ., РҫСҒРҪРҫРІР°РҪРҪСӢРј РҪР° РёР·РІРөСҒСӮРҪРҫР№ завиСҒРёРјРҫСҒСӮРё РјРөР¶РҙСғ РёСҒРәРҫРјРҫР№ РІРөлиСҮРёРҪРҫР№ Рё РҪРөРҝРҫСҒСҖРөРҙСҒСӮРІРөРҪРҪРҫ РёР·РјРөСҖСҸРөРјСӢРјРё РІРөлиСҮРёРҪами. В РЈСҒСӮР°РҪРҫРІР»РөРҪРҪСӢРө РҪР°СғРәРҫР№ СҒРІСҸР·Рё Рё РәРҫлиСҮРөСҒСӮРІРөРҪРҪСӢРө РҫСӮРҪРҫСҲРөРҪРёСҸ РјРөР¶РҙСғ СҖазлиСҮРҪСӢРјРё РҝРҫ СҒРІРҫРөР№ РҝСҖРёСҖРҫРҙРө физиСҮРөСҒРәРёРјРё СҸРІР»РөРҪРёСҸРјРё РҝРҫР·РІРҫлили СҒРҫР·РҙР°СӮСҢ СҒамРҫСҒРҫглаСҒРҫРІР°РҪРҪСғСҺ СҒРёСҒСӮРөРјСғ РөРҙРёРҪРёСҶ, РҝСҖРёРјРөРҪСҸРөРјСғСҺ РІРҫ РІСҒРөС… РҫРұлаСҒСӮСҸС… Рҳ. (СҒРј. РңРөР¶РҙСғРҪР°СҖРҫРҙРҪР°СҸ СҒРёСҒСӮРөРјР° РөРҙРёРҪРёСҶ ). В Рҳ. СҒР»РөРҙСғРөСӮ РҫСӮлиСҮР°СӮСҢ РҫСӮ РҙСҖСғРіРёС… РҝСҖиёмРҫРІ РәРҫлиСҮРөСҒСӮРІРөРҪРҪРҫР№ С…Р°СҖР°РәСӮРөСҖРёСҒСӮРёРәРё РІРөлиСҮРёРҪ, РҝСҖРёРјРөРҪСҸРөРјСӢС… РІ СӮРөС… СҒР»СғСҮР°СҸС…, РәРҫРіРҙР° РҪРөСӮ РҫРҙРҪРҫР·РҪР°СҮРҪРҫРіРҫ СҒРҫРҫСӮРІРөСӮСҒСӮРІРёСҸ РјРөР¶РҙСғ РІРөлиСҮРёРҪРҫР№ Рё РөС‘ РәРҫлиСҮРөСҒСӮРІРөРҪРҪСӢРј РІСӢСҖажРөРҪРёРөРј РІ РҫРҝСҖРөРҙРөлёРҪРҪСӢС… РөРҙРёРҪРёСҶах. РўР°Рә, РІРёР·СғалСҢРҪРҫРө РҫРҝСҖРөРҙРөР»РөРҪРёРө СҒРәРҫСҖРҫСҒСӮРё РІРөСӮСҖР° РҝРҫ Р‘РҫС„РҫСҖСӮР° СҲРәалРө или СӮРІС‘СҖРҙРҫСҒСӮРё РјРёРҪРөСҖалРҫРІ РҝРҫ РңРҫРҫСҒР° СҲРәалРө СҒР»РөРҙСғРөСӮ СҒСҮРёСӮР°СӮСҢ РҪРө Рҳ., Р° РҫСҶРөРҪРәРҫР№ . В Р’СҒСҸРәРҫРө Рҳ. РҪРөРёР·РұРөР¶РҪРҫ СҒРІСҸР·Р°РҪРҫ СҒ РҝРҫРіСҖРөСҲРҪРҫСҒСӮСҸРјРё РёР·РјРөСҖРөРҪРёР№. РҹРҫРіСҖРөСҲРҪРҫСҒСӮРё, РҝРҫСҖРҫР¶РҙРөРҪРҪСӢРө РҪРөСҒРҫРІРөСҖСҲРөРҪСҒСӮРІРҫРј РјРөСӮРҫРҙР° Рҳ., РҪРөСӮРҫСҮРҪРҫР№ РіСҖР°РҙСғРёСҖРҫРІРәРҫР№ Рё РҪРөРҝСҖавилСҢРҪРҫР№ СғСҒСӮР°РҪРҫРІРәРҫР№ РёР·РјРөСҖРёСӮРөР»СҢРҪРҫР№ Р°РҝРҝР°СҖР°СӮСғСҖСӢ, РҪазСӢРІР°СҺСӮ СҒРёСҒСӮРөРјР°СӮРёСҮРөСҒРәРёРјРё. РЎРёСҒСӮРөРјР°СӮРёСҮРөСҒРәРёРө РҝРҫРіСҖРөСҲРҪРҫСҒСӮРё РёСҒРәР»СҺСҮР°СҺСӮ РІРІРөРҙРөРҪРёРөРј РҝРҫРҝСҖавРҫРә, РҪайРҙРөРҪРҪСӢС… СҚРәСҒРҝРөСҖРёРјРөРҪСӮалСҢРҪРҫ. РҹРҫРіСҖРөСҲРҪРҫСҒСӮРё РҙСҖСғРіРҫРіРҫ СӮРёРҝР° - СҒР»СғСҮайРҪСӢРө - РҫРұСғСҒР»РҫРІР»РөРҪСӢ влиСҸРҪРёРөРј РҪР° СҖРөР·СғР»СҢСӮР°СӮ Рҳ. РҪРөРәРҫРҪСӮСҖРҫлиСҖСғРөРјСӢС… фаРәСӮРҫСҖРҫРІ (РёРјРё РјРҫРіСғСӮ РұСӢСӮСҢ, РҪР°РҝСҖРёРјРөСҖ, СҒР»СғСҮайРҪСӢРө РәРҫР»РөРұР°РҪРёСҸ СӮРөРјРҝРөСҖР°СӮСғСҖСӢ, РІРёРұСҖР°СҶРёРё Рё СӮ. Рҙ.). РЎР»СғСҮайРҪСӢРө РҝРҫРіСҖРөСҲРҪРҫСҒСӮРё РҫСҶРөРҪРёРІР°СҺСӮСҒСҸ РјРөСӮРҫРҙами РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ СҒСӮР°СӮРёСҒСӮРёРәРё РҝРҫ РҙР°РҪРҪСӢРј РјРҪРҫРіРҫРәСҖР°СӮРҪСӢС… Рҳ. (СҒРј. РқР°РұР»СҺРҙРөРҪРёР№ РҫРұСҖР°РұРҫСӮРәР° ). В Р’ РҪРөРәРҫСӮРҫСҖСӢС… СҒР»СғСҮР°СҸС… - РҫСҒРҫРұРөРҪРҪРҫ СҮР°СҒСӮРҫ РІСҒСӮСҖРөСҮР°СҺСүРёС…СҒСҸ РІ Р°СӮРҫРјРҪРҫР№ Рё СҸРҙРөСҖРҪРҫР№ физиРәРө - СҖазРұСҖРҫСҒ СҖРөР·СғР»СҢСӮР°СӮРҫРІ Рҳ. СҒРІСҸР·Р°РҪ РҪРө СӮРҫР»СҢРәРҫ СҒ РҝРҫРіСҖРөСҲРҪРҫСҒСӮСҸРјРё Р°РҝРҝР°СҖР°СӮСғСҖСӢ, РҪРҫ Рё СҒ С…Р°СҖР°РәСӮРөСҖРҫРј СҒамих РёСҒСҒР»РөРҙСғРөРјСӢС… СҸРІР»РөРҪРёР№. РқР°РҝСҖРёРјРөСҖ, РөСҒли РҝСғСҮРҫРә РҫРҙРёРҪР°РәРҫРІРҫ СғСҒРәРҫСҖРөРҪРҪСӢС… СҚР»РөРәСӮСҖРҫРҪРҫРІ РҝСҖРҫРҝСғСҒСӮРёСӮСҢ СҮРөСҖРөР· СүРөР»СҢ РҙРёС„СҖР°РәСҶРёРҫРҪРҪРҫР№ СҖРөСҲС‘СӮРәРё, СӮРҫ СҚР»РөРәСӮСҖРҫРҪСӢ СҒ РҫРҝСҖРөРҙРөлёРҪРҪРҫР№ РІРөСҖРҫСҸСӮРҪРҫСҒСӮСҢСҺ РҝРҫРҝР°РҙСғСӮ РІ СҖазРҪСӢРө СӮРҫСҮРәРё РҝРҫСҒСӮавлРөРҪРҪРҫРіРҫ Р·Р° СҖРөСҲС‘СӮРәРҫР№ СҚРәСҖР°РҪР° (СҒРј. ДифСҖР°РәСҶРёСҸ СҮР°СҒСӮРёСҶ ). РҹСҖРёРІРөРҙС‘РҪРҪСӢР№ РҝСҖРёРјРөСҖ РҝРҫРәазСӢРІР°РөСӮ, СҮСӮРҫ СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪРёРө Рҳ. РҪР° РҪРҫРІСӢРө РҫРұлаСҒСӮРё физиРәРё СӮСҖРөРұСғРөСӮ РҝРөСҖРөСҒРјРҫСӮСҖР° Рё СғСӮРҫСҮРҪРөРҪРёСҸ РҝРҫРҪСҸСӮРёР№, РәРҫСӮРҫСҖСӢРјРё РҫРҝРөСҖРёСҖСғСҺСӮ РҝСҖРё Рҳ. РІ РҙСҖСғРіРёС… РҫРұлаСҒСӮСҸС…. РЎ СҖазвиСӮРёРөРј РҪР°СғРәРё Рё СӮРөС…РҪРёРәРё РІРҫР·РҪРёРәла РөСүС‘ РҫРҙРҪР° важРҪР°СҸ РҝСҖРҫРұР»РөРјР° - авСӮРҫРјР°СӮРёР·Р°СҶРёСҸ Рҳ. РӯСӮРҫ СҒРІСҸР·Р°РҪРҫ, СҒ РҫРҙРҪРҫР№ СҒСӮРҫСҖРҫРҪСӢ, СҒ СғСҒР»РҫРІРёСҸРјРё, РІ РәРҫСӮРҫСҖСӢС… РҫСҒСғСүРөСҒСӮРІР»СҸСҺСӮСҒСҸ СҒРҫРІСҖРөРјРөРҪРҪСӢРө Рҳ. (СҸРҙРөСҖРҪСӢРө СҖРөР°РәСӮРҫСҖСӢ, РҫСӮРәСҖСӢСӮСӢР№ РәРҫСҒРјРҫСҒ Рё СӮ. Рҙ.), СҒ РҙСҖСғРіРҫР№ СҒСӮРҫСҖРҫРҪСӢ - СҒ РҪРөСҒРҫРІРөСҖСҲРөРҪСҒСӮРІРҫРј РҫСҖРіР°РҪРҫРІ СҮСғРІСҒСӮРІ СҮРөР»РҫРІРөРәР°. Р’ СҒРҫРІСҖРөРјРөРҪРҪРҫРј РҝСҖРҫРёР·РІРҫРҙСҒСӮРІРө, РҫСҒРҫРұРөРҪРҪРҫ РІ СғСҒР»РҫРІРёСҸС… РІСӢСҒРҫРәРёС… СҒРәРҫСҖРҫСҒСӮРөР№, РҙавлРөРҪРёР№, СӮРөРјРҝРөСҖР°СӮСғСҖ, РҪРөРҝРҫСҒСҖРөРҙСҒСӮРІРөРҪРҪРҫРө СҒРҫРөРҙРёРҪРөРҪРёРө РёР·РјРөСҖРёСӮРөР»СҢРҪСӢС… СғСҒСӮСҖРҫР№СҒСӮРІ СҒ СҖРөРіСғлиСҖСғСҺСүРёРјРё, РјРёРҪСғСҸ СҮРөР»РҫРІРөРәР°, РҝРҫР·РІРҫР»СҸРөСӮ РҝРөСҖРөР№СӮРё Рә РҪаиРұРҫР»РөРө СҒРҫРІРөСҖСҲРөРҪРҪРҫР№ С„РҫСҖРјРө РҝСҖРҫРёР·РІРҫРҙСҒСӮРІР° - авСӮРҫРјР°СӮРёР·РёСҖРҫРІР°РҪРҪРҫРјСғ РҝСҖРҫРёР·РІРҫРҙСҒСӮРІСғ. В Рҳ. РІ РјРөСӮСҖРҫР»РҫРіРёРё РҝРҫРҙСҖазРҙРөР»СҸСҺСӮСҒСҸ РҪР° РҝСҖСҸРјСӢРө, РәРҫСҒРІРөРҪРҪСӢРө, СҒРҫРІРҫРәСғРҝРҪСӢРө Рё СҒРҫРІРјРөСҒСӮРҪСӢРө. РҹСҖСҸРјСӢРјРё РҪазСӢРІР°СҺСӮСҒСҸ Рҳ., РҝСҖРё РәРҫСӮРҫСҖСӢС… РјРөСҖР° или РҝСҖРёРұРҫСҖ РҝСҖРёРјРөРҪСҸСҺСӮСҒСҸ РҪРөРҝРҫСҒСҖРөРҙСҒСӮРІРөРҪРҪРҫ РҙР»СҸ Рҳ. РҙР°РҪРҪРҫР№ РІРөлиСҮРёРҪСӢ (РҪР°РҝСҖРёРјРөСҖ, Рҳ. РјР°СҒСҒСӢ РҪР° СҶРёС„РөСҖРұлаСӮРҪСӢС… или СҖавРҪРҫРҝР»РөСҮРҪСӢС… РІРөСҒах, Рҳ. СӮРөРјРҝРөСҖР°СӮСғСҖСӢ СӮРөСҖРјРҫРјРөСӮСҖРҫРј). РҡРҫСҒРІРөРҪРҪСӢРјРё РҪазСӢРІР°СҺСӮСҒСҸ Рҳ., СҖРөР·СғР»СҢСӮР°СӮСӢ РәРҫСӮРҫСҖСӢС… РҪахРҫРҙСҸСӮ РҪР° РҫСҒРҪРҫРІР°РҪРёРё РёР·РІРөСҒСӮРҪРҫР№ завиСҒРёРјРҫСҒСӮРё РјРөР¶РҙСғ РёСҒРәРҫРјРҫР№ РІРөлиСҮРёРҪРҫР№ Рё РҪРөРҝРҫСҒСҖРөРҙСҒСӮРІРөРҪРҪРҫ РёР·РјРөСҖСҸРөРјСӢРјРё РІРөлиСҮРёРҪами (РҪР°РҝСҖРёРјРөСҖ, Рҳ. РҝР»РҫСӮРҪРҫСҒСӮРё РҫРҙРҪРҫСҖРҫРҙРҪРҫРіРҫ СӮРөла РҝРҫ РөРіРҫ РјР°СҒСҒРө Рё РіРөРҫРјРөСӮСҖРёСҮРөСҒРәРёРј СҖазмРөСҖам). РЎРҫРІРҫРәСғРҝРҪСӢРјРё РҪазСӢРІР°СҺСӮСҒСҸ Рҳ. РҪРөСҒРәРҫР»СҢРәРёС… РҫРҙРҪРҫРёРјС‘РҪРҪСӢС… РІРөлиСҮРёРҪ, Р·РҪР°СҮРөРҪРёСҸ РәРҫСӮРҫСҖСӢС… РҪахРҫРҙСҸСӮ СҖРөСҲРөРҪРёРөРј СҒРёСҒСӮРөРјСӢ СғСҖавРҪРөРҪРёР№, РҝРҫР»СғСҮР°РөРјСӢС… РІ СҖРөР·СғР»СҢСӮР°СӮРө РҝСҖСҸРјСӢС… Рҳ. СҖазлиСҮРҪСӢС… СҒРҫСҮРөСӮР°РҪРёР№ СҚСӮРёС… РІРөлиСҮРёРҪ (РҪР°РҝСҖРёРјРөСҖ, РәалиРұСҖРҫРІРәР° РҪР°РұРҫСҖР° РіРёСҖСҢ, РәРҫРіРҙР° Р·РҪР°СҮРөРҪРёСҸ РјР°СҒСҒ РіРёСҖСҢ РҪахРҫРҙСҸСӮ РҪР° РҫСҒРҪРҫРІР°РҪРёРё РҝСҖСҸРјРҫРіРҫ Рҳ. РјР°СҒСҒСӢ РҫРҙРҪРҫР№ РёР· РҪРёС… Рё СҒСҖавРҪРөРҪРёСҸ РјР°СҒСҒ СҖазлиСҮРҪСӢС… СҒРҫСҮРөСӮР°РҪРёР№ РіРёСҖСҢ). РЎРҫРІРјРөСҒСӮРҪСӢРө Рҳ. - РҝСҖРҫРёР·РІРҫРҙРёРјСӢРө РҫРҙРҪРҫРІСҖРөРјРөРҪРҪРҫ Рҳ. РҙРІСғС… или РҪРөСҒРәРҫР»СҢРәРёС… СҖазРҪРҫРёРјС‘РҪРҪСӢС… РІРөлиСҮРёРҪ СҒ СҶРөР»СҢСҺ РҪахРҫР¶РҙРөРҪРёСҸ завиСҒРёРјРҫСҒСӮРё РјРөР¶РҙСғ РҪРёРјРё (РҪР°РҝСҖРёРјРөСҖ, РҪахРҫР¶РҙРөРҪРёРө завиСҒРёРјРҫСҒСӮРё СғРҙлиРҪРөРҪРёСҸ СӮРөла РҫСӮ СӮРөРјРҝРөСҖР°СӮСғСҖСӢ).  РазлиСҮР°СҺСӮ СӮР°РәР¶Рө Р°РұСҒРҫР»СҺСӮРҪСӢРө Рё РҫСӮРҪРҫСҒРёСӮРөР»СҢРҪСӢРө Рҳ. Рҡ РҝРөСҖРІСӢРј РҫСӮРҪРҫСҒСҸСӮ РәРҫСҒРІРөРҪРҪСӢРө Рҳ., РҫСҒРҪРҫРІР°РҪРҪСӢРө РҪР° Рҳ. РҫРҙРҪРҫР№ или РҪРөСҒРәРҫР»СҢРәРёС… РҫСҒРҪРҫРІРҪСӢС… РІРөлиСҮРёРҪ (РҪР°РҝСҖРёРјРөСҖ, РҙлиРҪСӢ, РјР°СҒСҒСӢ, РІСҖРөРјРөРҪРё) Рё РёСҒРҝРҫР»СҢР·РҫРІР°РҪРёРё Р·РҪР°СҮРөРҪРёР№ С„СғРҪРҙамРөРҪСӮалСҢРҪСӢС… физиСҮРөСҒРәРёС… РҝРҫСҒСӮРҫСҸРҪРҪСӢС… , СҮРөСҖРөР· РәРҫСӮРҫСҖСӢРө РёР·РјРөСҖСҸРөРјР°СҸ физиСҮРөСҒРәР°СҸ РІРөлиСҮРёРҪР° РјРҫР¶РөСӮ РұСӢСӮСҢ РІСӢСҖажРөРҪР°. РҹРҫРҙ РІСӮРҫСҖСӢРјРё РҝРҫРҪРёРјР°СҺСӮ Рҳ. лиРұРҫ РҫСӮРҪРҫСҲРөРҪРёСҸ РІРөлиСҮРёРҪСӢ Рә РҫРҙРҪРҫРёРјС‘РҪРҪРҫР№ РІРөлиСҮРёРҪРө, РёРіСҖР°СҺСүРөР№ СҖРҫР»СҢ РҝСҖРҫРёР·РІРҫР»СҢРҪРҫР№ РөРҙРёРҪРёСҶСӢ, лиРұРҫ РёР·РјРөРҪРөРҪРёСҸ РІРөлиСҮРёРҪСӢ РҫСӮРҪРҫСҒРёСӮРөР»СҢРҪРҫ РҙСҖСғРіРҫР№, РҝСҖРёРҪРёРјР°РөРјРҫР№ Р·Р° РёСҒС…РҫРҙРҪСғСҺ. В РқайРҙРөРҪРҪРҫРө РІ СҖРөР·СғР»СҢСӮР°СӮРө Рҳ. Р·РҪР°СҮРөРҪРёРө РёР·РјРөСҖСҸРөРјРҫР№ РІРөлиСҮРёРҪСӢ РҝСҖРөРҙСҒСӮавлСҸРөСӮ СҒРҫРұРҫР№ РҝСҖРҫРёР·РІРөРҙРөРҪРёРө РҫСӮРІР»РөСҮС‘РҪРҪРҫРіРҫ СҮРёСҒла (СҮРёСҒР»РҫРІРҫРіРҫ Р·РҪР°СҮРөРҪРёСҸ) РҪР° РөРҙРёРҪРёСҶСғ РҙР°РҪРҪРҫР№ РІРөлиСҮРёРҪСӢ. В Р РөР·СғР»СҢСӮР°СӮСӢ Рҳ. РёР·-Р·Р° РҝРҫРіСҖРөСҲРҪРҫСҒСӮРөР№ РІСҒРөРіРҙР° РҪРөСҒРәРҫР»СҢРәРҫ РҫСӮлиСҮР°СҺСӮСҒСҸ РҫСӮ РёСҒСӮРёРҪРҪРҫРіРҫ Р·РҪР°СҮРөРҪРёСҸ РёР·РјРөСҖСҸРөРјРҫР№ РІРөлиСҮРёРҪСӢ, РҝРҫСҚСӮРҫРјСғ СҖРөР·СғР»СҢСӮР°СӮСӢ Рҳ. РҫРұСӢСҮРҪРҫ СҒРҫРҝСҖРҫРІРҫР¶РҙР°СҺСӮ СғРәазаРҪРёРөРј РҫСҶРөРҪРәРё РҝРҫРіСҖРөСҲРҪРҫСҒСӮРё (СҒРј. РҹРҫРіСҖРөСҲРҪРҫСҒСӮРё РёР·РјРөСҖРөРҪРёР№ ). В РһРұРөСҒРҝРөСҮРөРҪРёРө РөРҙРёРҪСҒСӮРІР° Рҳ. РІ СҒСӮСҖР°РҪРө РІРҫзлагаРөСӮСҒСҸ РҪР° РјРөСӮСҖРҫР»РҫРіРёСҮРөСҒРәСғСҺ СҒР»СғР¶РұСғ, С…СҖР°РҪСҸСүСғСҺ СҚСӮалРҫРҪСӢ РөРҙРёРҪРёСҶ Рё РҝСҖРҫРёР·РІРҫРҙСҸСүСғСҺ РҝРҫРІРөСҖРәСғ РҝСҖРёРјРөРҪСҸРөРјСӢС… СҒСҖРөРҙСҒСӮРІ Рҳ. РЁРёСҖРҫРәРҫРө СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪРёРө РҝРҫР»СғСҮила РәлаСҒСҒифиРәР°СҶРёСҸ Рҳ. РҝРҫ РҫРұСҠРөРәСӮам Рҳ. РЎРҫглаСҒРҪРҫ РөР№, СҖазлиСҮР°СҺСӮ Рҳ. лиРҪРөР№РҪСӢРө (Рҳ. РҙлиРҪСӢ, РҝР»РҫСүР°РҙРё, РҫРұСҠёма), РјРөС…Р°РҪРёСҮРөСҒРәРёРө (Рҳ. СҒРёР»СӢ, РҙавлРөРҪРёСҸ Рё РҝСҖ.), СҚР»РөРәСӮСҖРёСҮРөСҒРәРёРө Рё СӮ. Рҙ. Р’ РҫРұСүРөРј СҚСӮР° РәлаСҒСҒифиРәР°СҶРёСҸ СҒРҫРҫСӮРІРөСӮСҒСӮРІСғРөСӮ РҫСҒРҪРҫРІРҪСӢРј СҖазРҙРөлам физиРәРё. В РӣРёСӮ.:РңалиРәРҫРІ РЎ. РӨ., РўСҺСҖРёРҪ Рқ. Рҳ., Р’РІРөРҙРөРҪРёРө РІ РјРөСӮСҖРҫР»РҫРіРёСҺ, 2 РёР·Рҙ., Рң., 1966; РңалиРәРҫРІ РЎ. РӨ., Р’РІРөРҙРөРҪРёРө РІ СӮРөС…РҪРёРәСғ РёР·РјРөСҖРөРҪРёР№, 2 РёР·Рҙ., Рң., 1952; РҜРҪРҫСҲРё Рӣ., РўРөРҫСҖРёСҸ Рё РҝСҖР°РәСӮРёРәР° РҫРұСҖР°РұРҫСӮРәРё СҖРөР·СғР»СҢСӮР°СӮРҫРІ РёР·РјРөСҖРөРҪРёР№, РҝРөСҖ. СҒ Р°РҪРіР»., 2 РёР·Рҙ., Рң., 1968; В«РҳР·РјРөСҖРёСӮРөР»СҢРҪР°СҸ СӮРөС…РҪРёРәа», 1961, в„– 12: 1962, в„– 4, 6, 8, 9, 10. В Рҡ. Рҹ. РЁРёСҖРҫРәРҫРІ.
В Р’ РјР°СӮРөРјР°СӮРёСҮРөСҒРәРҫР№ СӮРөРҫСҖРёРё Рҳ. РҫСӮРІР»РөРәР°СҺСӮСҒСҸ РҫСӮ РҫРіСҖР°РҪРёСҮРөРҪРҪРҫР№ СӮРҫСҮРҪРҫСҒСӮРё физиСҮРөСҒРәРёС… Рҳ. Р—Р°РҙР°СҮР° Рҳ. РІРөлиСҮРёРҪСӢ QРҝСҖРё РҝРҫРјРҫСүРё РөРҙРёРҪРёСҶСӢ РјРөСҖСӢ UСҒРҫСҒСӮРҫРёСӮ РІ РҪахРҫР¶РҙРөРҪРёРё СҮРёСҒР»РҫРІРҫРіРҫ РјРҪРҫжиСӮРөР»СҸ qРІ СҖавРөРҪСҒСӮРІРө
РҝСҖРё СҚСӮРҫРј QРё UСҒСҮРёСӮР°СҺСӮСҒСҸ РҝРҫР»РҫжиСӮРөР»СҢРҪСӢРјРё СҒРәалСҸСҖРҪСӢРјРё РІРөлиСҮРёРҪами РҫРҙРҪРҫРіРҫ Рё СӮРҫРіРҫ Р¶Рө СҖРҫРҙР° (СҒРј. Р’РөлиСҮРёРҪР° ), Р° РјРҪРҫжиСӮРөР»СҢ q -РҝРҫР»РҫжиСӮРөР»СҢРҪРҫРө РҙРөР№СҒСӮРІРёСӮРөР»СҢРҪРҫРө СҮРёСҒР»Рҫ, РәРҫСӮРҫСҖРҫРө РјРҫР¶РөСӮ РұСӢСӮСҢ РәР°Рә СҖР°СҶРёРҫРҪалСҢРҪСӢРј, СӮР°Рә Рё РёСҖСҖР°СҶРёРҫРҪалСҢРҪСӢРј. ДлСҸ СҖР°СҶРёРҫРҪалСҢРҪРҫРіРҫ q= m/n( mРё n -РҪР°СӮСғСҖалСҢРҪСӢРө СҮРёСҒла) СҖавРөРҪСҒСӮРІРҫ (1) РёРјРөРөСӮ РІРөСҒСҢРјР° РҝСҖРҫСҒСӮРҫР№ СҒРјСӢСҒР»: РҫРҪРҫ РҫР·РҪР°СҮР°РөСӮ, СҮСӮРҫ СҒСғСүРөСҒСӮРІСғРөСӮ СӮР°РәР°СҸ РІРөлиСҮРёРҪР° V( n-СҸ РҙРҫР»СҸ РҫСӮ U), РәРҫСӮРҫСҖР°СҸ, РұСғРҙСғСҮРё РІР·СҸСӮР° СҒлагаРөРјСӢРј nСҖаз, РҙаёСӮ U,РұСғРҙСғСҮРё Р¶Рө РІР·СҸСӮР° СҒлагаРөРјСӢРј mСҖаз, РҙаёСӮ Q:
В Р’ СҚСӮРҫРј СҒР»СғСҮР°Рө РІРөлиСҮРёРҪСӢ QРё UРҪазСӢРІР°СҺСӮСҒСҸ СҒРҫРёР·РјРөСҖРёРјСӢРјРё. ДлСҸ РҪРөСҒРҫРёР·РјРөСҖРёРјСӢС… РІРөлиСҮРёРҪ UРё QРјРҪРҫжиСӮРөР»СҢ qРёСҖСҖР°СҶРёРҫРҪалРөРҪ (РҪР°РҝСҖРёРјРөСҖ, СҖавРөРҪ СҮРёСҒР»Сғ p, РөСҒли QРөСҒСӮСҢ РҙлиРҪР° РҫРәСҖСғР¶РҪРҫСҒСӮРё, Р° U -РөС‘ РҙиамРөСӮСҖ). Р’ СҚСӮРҫРј СҒР»СғСҮР°Рө СҒамРҫРө РҫРҝСҖРөРҙРөР»РөРҪРёРө СҒРјСӢСҒла СҖавРөРҪСҒСӮРІР° (1) РҪРөСҒРәРҫР»СҢРәРҫ СҒР»РҫР¶РҪРөРө. РңРҫР¶РҪРҫ РҫРҝСҖРөРҙРөлиСӮСҢ РөРіРҫ СӮР°Рә: СҖавРөРҪСҒСӮРІРҫ (1) РҫРұРҫР·РҪР°СҮР°РөСӮ, СҮСӮРҫ РҙР»СҸ Р»СҺРұРҫРіРҫ СҖР°СҶРёРҫРҪалСҢРҪРҫРіРҫ СҮРёСҒла r
Р”РҫСҒСӮР°СӮРҫСҮРҪРҫ РҝРҫСӮСҖРөРұРҫРІР°СӮСҢ, СҮСӮРҫРұСӢ СғСҒР»РҫРІРёРө (2) РІСӢРҝРҫР»РҪСҸР»РҫСҒСҢ РҙР»СҸ РІСҒРөС… РҙРөСҒСҸСӮРёСҮРҪСӢС… РҝСҖРёРұлижРөРҪРёР№ Рә qРҝРҫ РҪРөРҙРҫСҒСӮР°СӮРәСғ Рё РҝРҫ РёР·РұСӢСӮРәСғ. РЎР»РөРҙСғРөСӮ РҫСӮРјРөСӮРёСӮСҢ, СҮСӮРҫ РёСҒСӮРҫСҖРёСҮРөСҒРәРё СҒамРҫ РҝРҫРҪСҸСӮРёРө РёСҖСҖР°СҶРёРҫРҪалСҢРҪРҫРіРҫ СҮРёСҒла РІРҫР·РҪРёРәР»Рҫ РёР· Р·Р°РҙР°СҮРё Рҳ., СӮР°Рә СҮСӮРҫ РҝРөСҖРІРҫРҪР°СҮалСҢРҪР°СҸ Р·Р°РҙР°СҮР° РІ СҒР»СғСҮР°Рө РҪРөСҒРҫРёР·РјРөСҖРёРјСӢС… РІРөлиСҮРёРҪ Р·Р°РәР»СҺСҮалаСҒСҢ СҒРҫРұСҒСӮРІРөРҪРҪРҫ РҪРө РІ СӮРҫРј, СҮСӮРҫРұСӢ РҫРҝСҖРөРҙРөлиСӮСҢ СҒРјСӢСҒР» СҖавРөРҪСҒСӮРІР° (1), РёСҒС…РҫРҙСҸ РёР· РіРҫСӮРҫРІРҫР№ СӮРөРҫСҖРёРё РҙРөР№СҒСӮРІРёСӮРөР»СҢРҪСӢС… СҮРёСҒРөР», Р° РІ СӮРҫРј, СҮСӮРҫРұСӢ СғСҒСӮР°РҪРҫРІРёСӮСҢ СҒРјСӢСҒР» СҒРёРјРІРҫла q, РҫСӮРҫРұСҖажаСҺСүРөРіРҫ СҖРөР·СғР»СҢСӮР°СӮ СҒСҖавРҪРөРҪРёСҸ РІРөлиСҮРёРҪСӢ QСҒ РөРҙРёРҪРёСҶРөР№ РјРөСҖСӢ U.РқР°РҝСҖРёРјРөСҖ, РҝРҫ РҫРҝСҖРөРҙРөР»РөРҪРёСҺ РҪРөРјРөСҶРәРҫРіРҫ РјР°СӮРөРјР°СӮРёРәР° Р . Р”РөРҙРөРәРёРҪРҙР°, РёСҖСҖР°СҶРёРҫРҪалСҢРҪРҫРө СҮРёСҒР»Рҫ РөСҒСӮСҢ В«СҒРөСҮРөРҪРёРөВ» РІ СҒРёСҒСӮРөРјРө СҖР°СҶРёРҫРҪалСҢРҪСӢС… СҮРёСҒРөР». РўР°РәРҫРө СҒРөСҮРөРҪРёРө Рё РҝРҫСҸРІР»СҸРөСӮСҒСҸ РөСҒСӮРөСҒСӮРІРөРҪРҪРҫ РҝСҖРё СҒСҖавРҪРөРҪРёРё РҙРІСғС… РҪРөСҒРҫРёР·РјРөСҖРёРјСӢС… РІРөлиСҮРёРҪ QРё U.РҹРҫ РҫСӮРҪРҫСҲРөРҪРёСҺ Рә СҚСӮРёРј РІРөлиСҮРёРҪам РІСҒРө СҖР°СҶРёРҫРҪалСҢРҪСӢРө СҮРёСҒла СҖазРҙРөР»СҸСҺСӮСҒСҸ РҪР° РҙРІР° РәлаСҒСҒР°: РәлаСҒСҒ R 1СҖР°СҶРёРҫРҪалСҢРҪСӢС… СҮРёСҒРөР» r, РҙР»СҸ РәРҫСӮРҫСҖСӢС… Q> rU, Рё РәлаСҒСҒ R 2СҖР°СҶРёРҫРҪалСҢРҪСӢС… СҮРёСҒРөР» r, РҙР»СҸ РәРҫСӮРҫСҖСӢС… Q< rU. В Р‘РҫР»СҢСҲРҫРө Р·РҪР°СҮРөРҪРёРө РёРјРөРөСӮ РҝСҖРёРұлижёРҪРҪРҫРө Рҳ. РІРөлиСҮРёРҪ РҝСҖРё РҝРҫРјРҫСүРё СҖР°СҶРёРҫРҪалСҢРҪСӢС… СҮРёСҒРөР». РһСҲРёРұРәР° РҝСҖРёРұлижёРҪРҪРҫРіРҫ СҖавРөРҪСҒСӮРІР° QВ» rUСҖавРҪР° D = ( r- qU). Р•СҒСӮРөСҒСӮРІРөРҪРҪРҫ РёСҒРәР°СӮСҢ СӮР°РәРёРө r= m/ n,РҙР»СҸ РәРҫСӮРҫСҖСӢС… РҫСҲРёРұРәР° РјРөРҪСҢСҲРө, СҮРөРј РҝСҖРё Р»СҺРұРҫРј СҮРёСҒР»Рө r'= mвҖҷ/ nвҖҷСҒ Р·РҪамРөРҪР°СӮРөР»РөРј n'РҲ n.РўР°РәРҫРіРҫ СҖРҫРҙР° РҝСҖРёРұлижРөРҪРёСҸ РҙРҫСҒСӮавлСҸСҺСӮСҒСҸ РҝРҫРҙС…РҫРҙСҸСүРёРјРё РҙСҖРҫРұСҸРјРё r 1, r 2, r 3,... Рә СҮРёСҒР»Сғ q, РәРҫСӮРҫСҖСӢРө РҪахРҫРҙСҸСӮСҒСҸ РҝСҖРё РҝРҫРјРҫСүРё СӮРөРҫСҖРёРё РҪРөРҝСҖРөСҖСӢРІРҪСӢС… РҙСҖРҫРұРөР№ . РқР°РҝСҖРёРјРөСҖ, РҙР»СҸ РҙлиРҪСӢ РҫРәСҖСғР¶РҪРҫСҒСӮРё S, РёР·РјРөСҖСҸРөРјРҫР№ РҙиамРөСӮСҖРҫРј U,РҝСҖРёРұлижРөРҪРёСҸ СӮР°РәРҫРІСӢ:
Рё СӮ. Рҙ.; РҙР»СҸ РҙлиРҪСӢ РіРҫРҙР° Q, РёР·РјРөСҖСҸРөРјРҫР№ СҒСғСӮРәами U, РҝСҖРёРұлижРөРҪРёСҸ СӮР°РәРҫРІСӢ:
В Рҗ. Рқ. РҡРҫлмРҫРіРҫСҖРҫРІ. В Рҳ. РІ СҒРҫСҶиалСҢРҪРҫРј РёСҒСҒР»РөРҙРҫРІР°РҪРёРё (РІ СҒСӮР°СӮРёСҒСӮРёРәРө, СҒРҫСҶРёРҫР»РҫРіРёРё, РҝСҒРёС…РҫР»РҫРіРёРё, СҚРәРҫРҪРҫРјРёРәРө, СҚСӮРҪРҫРіСҖафии), СҒРҝРҫСҒРҫРұ СғРҝРҫСҖСҸРҙРҫСҮРөРҪРёСҸ СҒРҫСҶиалСҢРҪРҫР№ РёРҪС„РҫСҖРјР°СҶРёРё, РҝСҖРё РәРҫСӮРҫСҖРҫРј СҒРёСҒСӮРөРјСӢ СҮРёСҒРөР» Рё РҫСӮРҪРҫСҲРөРҪРёР№ РјРөР¶РҙСғ РҪРёРјРё СҒСӮавСҸСӮСҒСҸ РІ СҒРҫРҫСӮРІРөСӮСҒСӮРІРёРө СҖСҸРҙСғ РёР·РјРөСҖСҸРөРјСӢС… СҒРҫСҶиалСҢРҪСӢС… фаРәСӮРҫРІ. РазлиСҮРҪСӢРө РјРөСҖСӢ РҝРҫРІСӮРҫСҖСҸРөРјРҫСҒСӮРё, РІРҫСҒРҝСҖРҫРёР·РІРҫРҙРёРјРҫСҒСӮРё СҒРҫСҶиалСҢРҪСӢС… фаРәСӮРҫРІ Рё СҸРІР»СҸСҺСӮСҒСҸ СҒРҫСҶиалСҢРҪСӢРјРё РёР·РјРөСҖРөРҪРёСҸРјРё, или СҲРәалами. РЎ СҖазвиСӮРёРөРј РҫРұСүРөСҒСӮРІР° РҝРҫР»СғСҮР°СҺСӮ СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪРёРө РҝСҖРҫСҒСӮСӢРө СҲРәалСӢ - РҙРөРҪРөР¶РҪР°СҸ РҫСҶРөРҪРәР° СӮСҖСғРҙР°, СҖазСҖСҸРҙСӢ РәвалифиРәР°СҶРёРё, РҫСҶРөРҪРәР° СғСҒРҝРөС…РҫРІ РІ РҫРұСғСҮРөРҪРёРё (СҒРёСҒСӮРөРјР° РұаллРҫРІ), СҒРҝРҫСҖСӮРө Рё РҙСҖ. Рҳ. РІ РҫРұСүРөСҒСӮРІРөРҪРҪСӢС… РҪР°СғРәах РҫСӮлиСҮР°РөСӮСҒСҸ РҫСӮ СӮР°РәРёС… В«РөСҒСӮРөСҒСӮРІРөРҪРҪСӢС…В» СҲРәал СӮРҫСҮРҪСӢРј РҫРҝСҖРөРҙРөР»РөРҪРёРөРј РёР·РјРөСҖСҸРөРјСӢС… РҝСҖРёР·РҪР°РәРҫРІ Рё РҝСҖавил РҝРҫСҒСӮСҖРҫРөРҪРёСҸ СҲРәалСӢ. В Р’ СҒРҫСҶиалСҢРҪСӢС… РёСҒСҒР»РөРҙРҫРІР°РҪРёСҸС… Рҳ. РІРҝРөСҖРІСӢРө РІРҫСҲли РІ СғРҝРҫСӮСҖРөРұР»РөРҪРёРө РІ 1920-30, РәРҫРіРҙР° РёСҒСҒР»РөРҙРҫРІР°СӮРөли СҒСӮРҫР»РәРҪСғлиСҒСҢ СҒ РҝСҖРҫРұР»РөРјРҫР№ РҙРҫСҒСӮРҫРІРөСҖРҪРҫСҒСӮРё РҝСҖРё РёР·СғСҮРөРҪРёРё РҫРұСүРөСҒСӮРІРөРҪРҪРҫРіРҫ СҒРҫР·РҪР°РҪРёСҸ, СҒРҫСҶиалСҢРҪРҫ-РҝСҒРёС…РҫР»РҫРіРёСҮРөСҒРәРёС… СғСҒСӮР°РҪРҫРІРҫРә (РҫСӮРҪРҫСҲРөРҪРёР№), СҒРҫСҶиалСҢРҪРҫРіРҫ Рё РҝСҖРҫС„РөСҒСҒРёРҫРҪалСҢРҪРҫРіРҫ СҒСӮР°СӮСғСҒРҫРІ, РҫРұСүРөСҒСӮРІРөРҪРҪРҫРіРҫ РјРҪРөРҪРёСҸ, РәР°СҮРөСҒСӮРІРөРҪРҪСӢС… С…Р°СҖР°РәСӮРөСҖРёСҒСӮРёРә СғСҒР»РҫРІРёР№ СӮСҖСғРҙР° Рё РұСӢСӮР° Рё СӮ. Рҙ. РӯСӮРё Рҳ. СҸРІР»СҸСҺСӮСҒСҸ РҝСҖРёРјРөСҖРҫРј СҒСӮР°РҪРҙР°СҖСӮРёР·РҫРІР°РҪРҪРҫР№ РіСҖСғРҝРҝРҫРІРҫР№ РҫСҶРөРҪРәРё, РәРҫРіРҙР° СҒ РҝРҫРјРҫСүСҢСҺ РјРөСӮРҫРҙРҫРІ РІСӢРұРҫСҖРҫСҮРҪРҫР№ СҒСӮР°СӮРёСҒСӮРёРәРё РёР·РјРөСҖСҸРөСӮСҒСҸ «иРҪСӮРөРҪСҒРёРІРҪРҫСҒСӮСҢВ» РҫРұСүРөСҒСӮРІРөРҪРҪРҫРіРҫ РјРҪРөРҪРёСҸ. В Рҳ. СҖазРҙРөР»СҸСҺСӮСҒСҸ РҪР° СӮСҖРё СӮРёРҝР°: 1) РҪРҫРјРёРҪалСҢРҪРҫРө - СҮРёСҒла, РҝСҖРёРҝРёСҒСӢРІР°РөРјСӢРө РҫРұСҠРөРәСӮам РҪР° РҪРҫРјРёРҪалСҢРҪРҫР№ СҲРәалРө, лиСҲСҢ РәРҫРҪСҒСӮР°СӮРёСҖСғСҺСӮ РҫСӮлиСҮРёРө или СӮРҫР¶РҙРөСҒСӮРІРҫ СҚСӮРёС… РҫРұСҠРөРәСӮРҫРІ, СӮ. Рө. РҪРҫРјРёРҪалСҢРҪР°СҸ СҲРәала РөСҒСӮСҢ, РҝРҫ СҒСғСүРөСҒСӮРІСғ, РіСҖСғРҝРҝРёСҖРҫРІРәР° или РәлаСҒСҒифиРәР°СҶРёСҸ. 2) РҝРҫСҖСҸРҙРәРҫРІРҫРө - СҮРёСҒла, РҝСҖРёРҝРёСҒСӢРІР°РөРјСӢРө РҫРұСҠРөРәСӮам РҪР° СҲРәалРө, СғРҝРҫСҖСҸРҙРҫСҮРёРІР°СҺСӮ РёС… РҝРҫ РёР·РјРөСҖСҸРөРјРҫРјСғ РҝСҖРёР·РҪР°РәСғ, РҪРҫ СғРәазСӢРІР°СҺСӮ лиСҲСҢ РҪР° РҝРҫСҖСҸРҙРҫРә СҖазмРөСүРөРҪРёСҸ РҫРұСҠРөРәСӮРҫРІ РҪР° СҲРәалРө, Р° РҪРө РҪР° СҖР°СҒСҒСӮРҫСҸРҪРёРө РјРөР¶РҙСғ РҫРұСҠРөРәСӮами или, СӮРөРј РұРҫР»РөРө, РәРҫРҫСҖРҙРёРҪР°СӮСӢ; 3) РёРҪСӮРөСҖвалСҢРҪРҫРө - СҮРёСҒла, РҝСҖРёРҝРёСҒСӢРІР°РөРјСӢРө РҫРұСҠРөРәСӮам РҪР° СҲРәалРө, СғРәазСӢРІР°СҺСӮ РҪРө СӮРҫР»СҢРәРҫ РҪР° РҝРҫСҖСҸРҙРҫРә РҫРұСҠРөРәСӮРҫРІ, РҪРҫ Рё РҪР° СҖР°СҒСҒСӮРҫСҸРҪРёРө РјРөР¶РҙСғ РҪРёРјРё. РҳРҪСӮРөСҖвалСҢРҪСӢРј Рҳ. СҸРІР»СҸРөСӮСҒСҸ, РҪР°РҝСҖРёРјРөСҖ, СҲРәала РҝСҖРёРІР»РөРәР°СӮРөР»СҢРҪРҫСҒСӮРё РҝСҖРҫС„РөСҒСҒРёР№. РўР°РәР°СҸ СҲРәала, РҝСҖРёРҙаваСҸ РәажРҙРҫР№ РҝСҖРҫС„РөСҒСҒРёРё СғСҒР»РҫРІРҪСӢР№ Рұалл, РҝРҫР·РІРҫР»СҸРөСӮ СҒСҖавРҪРёРІР°СӮСҢ РҝСҖРҫС„РөСҒСҒРёРё РҝРҫ РҝРҫРҝСғР»СҸСҖРҪРҫСҒСӮРё, СӮ. Рө. СғСӮРІРөСҖР¶РҙР°СӮСҢ, СҮСӮРҫ, РҪР°РҝСҖРёРјРөСҖ, РҝСҖРҫС„РөСҒСҒРёСҸ СҲРҫфёСҖР° РҪР° РңРұаллРҫРІ РҝРҫРҝСғР»СҸСҖРҪРөРө РҝСҖРҫС„РөСҒСҒРёРё СҒР»РөСҒР°СҖСҸ Рё РҪР° РҡРұаллРҫРІ РјРөРҪРөРө РҝРҫРҝСғР»СҸСҖРҪР°, СҮРөРј РҝСҖРҫС„РөСҒСҒРёСҸ лёСӮСҮРёРәР°. РһРҙРҪР°РәРҫ РҫРҪР° РҪРө РҝРҫР·РІРҫР»СҸРөСӮ СғСӮРІРөСҖР¶РҙР°СӮСҢ, СҮСӮРҫ РёРҪСӮРөСҖРөСҒ Рә РҝСҖРҫС„РөСҒСҒРёСҸРј СҲРҫфёСҖР° Рё СҒР»РөСҒР°СҖСҸ РҝСҖРөРІСӢСҲР°РөСӮ РёРҪСӮРөСҖРөСҒ Рә РҝСҖРҫС„РөСҒСҒРёРё лёСӮСҮРёРәР°, РөСҒли СҒСғРјРјР° СҒРҫРҫСӮРІРөСӮСҒСӮРІСғСҺСүРёС… РұаллРҫРІ РҝСҖРөРІСӢСҲР°РөСӮ Рұалл РҝСҖРҫС„РөСҒСҒРёРё лёСӮСҮРёРәР°. РқахРҫР¶РҙРөРҪРёРө РәРҫлиСҮРөСҒСӮРІРөРҪРҪРҫР№ РјРөСҖСӢ СҒРҫСҶиалСҢРҪСӢС… СҸРІР»РөРҪРёР№ Рё РҝСҖРҫСҶРөСҒСҒРҫРІ РҫРіСҖР°РҪРёСҮРёРІР°РөСӮСҒСҸ СҚСӮРёРјРё СӮСҖРөРјСҸ СӮРёРҝами Рҳ. РҹСҖРөРҙРҝСҖРёРҪРёРјР°СҺСӮСҒСҸ РҝРҫРҝСӢСӮРәРё СҒРҫР·РҙР°РҪРёСҸ СҮРөСӮРІС‘СҖСӮРҫРіРҫ СӮРёРҝР° Рҳ. - РәРҫлиСҮРөСҒСӮРІРөРҪРҪРҫРіРҫ, СҒ РІРІРөРҙРөРҪРёРөРј РөРҙРёРҪРёСҶСӢ Рҳ. В РӣРёСӮ.:РҜРҙРҫРІ Р’. Рҗ., РңРөСӮРҫРҙРҫР»РҫРіРёСҸ Рё РҝСҖРҫСҶРөРҙСғСҖСӢ СҒРҫСҶРёРҫР»РҫРіРёСҮРөСҒРәРёС… РёСҒСҒР»РөРҙРҫРІР°РҪРёР№, РўР°СҖСӮСғ, 1968; Р—РҙСҖавРҫРјСӢСҒР»РҫРІ Рҗ. Р“., РңРөСӮРҫРҙРҫР»РҫРіРёСҸ Рё РҝСҖРҫСҶРөРҙСғСҖР° СҒРҫСҶРёРҫР»РҫРіРёСҮРөСҒРәРёС… РёСҒСҒР»РөРҙРҫРІР°РҪРёР№, Рң., 1969. В Р®. Р‘. СамСҒРҫРҪРҫРІ. РҳР·РјРөСҖРөРҪРёРө живРҫСӮРҪСӢС… РҳР·РјРөСҖРө'РҪРёРө живРҫ'СӮРҪСӢС…,РҫРұРјРөСҖ СҖазлиСҮРҪСӢС… СҮР°СҒСӮРөР№ (СҒСӮР°СӮРөР№) СӮРөла живРҫСӮРҪСӢС…. РҹСҖРҫРІРҫРҙРёСӮСҒСҸ РҝСҖРё РҫСҶРөРҪРәРө СҚРәСҒСӮРөСҖСҢРөСҖР° Рё РәРҫРҪСҒСӮРёСӮСғСҶРёРё живРҫСӮРҪСӢС…, РҙР»СҸ РҫРҝСҖРөРҙРөР»РөРҪРёСҸ живРҫР№ РјР°СҒСҒСӢ живРҫСӮРҪСӢС… РұРөР· РІР·РІРөСҲРёРІР°РҪРёСҸ, РҙР»СҸ РәРҫРҪСӮСҖРҫР»СҸ Р·Р° СҖРҫСҒСӮРҫРј Рё СҖазвиСӮРёРөРј РјРҫР»РҫРҙРҪСҸРәР° Рё СӮ.Рҝ. РазлиСҮР°СҺСӮ 4 РҫСҒРҪРҫРІРҪСӢРө РіСҖСғРҝРҝСӢ РҝСҖРҫРјРөСҖРҫРІ: РІСӢСҒРҫСӮРҪСӢРө, РҝСҖРҫРјРөСҖСӢ РҙлиРҪСӢ, СҲРёСҖРҫСӮРҪСӢРө Рё РҫРұС…РІР°СӮСӢ (РҝСҖРҫРјРөСҖСӢ РіСҖСғРҙРё Рё РәРҫРҪРөСҮРҪРҫСҒСӮРөР№). Р’ завиСҒРёРјРҫСҒСӮРё РҫСӮ РҝРҫСҒСӮавлРөРҪРҪСӢС… Р·Р°РҙР°СҮ Рё РІРёРҙРҫРІСӢС… РҫСҒРҫРұРөРҪРҪРҫСҒСӮРөР№ живРҫСӮРҪСӢС… РҫРҝСҖРөРҙРөР»СҸСҺСӮ СҖазлиСҮРҪРҫРө СҮРёСҒР»Рҫ РҝСҖРҫРјРөСҖРҫРІ: РҝСҖРё РҪР°СғСҮРҪСӢС… РёСҒСҒР»РөРҙРҫРІР°РҪРёСҸС…, СӮСҖРөРұСғСҺСүРёС… РҝРҫРҙСҖРҫРұРҪРҫРіРҫ РҫРұСҒР»РөРҙРҫРІР°РҪРёСҸ живРҫСӮРҪСӢС…, - РҫСӮ 28 РҙРҫ 52; РҝСҖРё Р·Р°РҝРёСҒРё РІ РҝР»РөРјРөРҪРҪСӢРө РәРҪРёРіРё, РҪР°РҝСҖРёРјРөСҖ, РәСҖСғРҝРҪРҫРіРҫ СҖРҫРіР°СӮРҫРіРҫ СҒРәРҫСӮР° - 12, Р»РҫСҲР°РҙРөР№ - 4, СҒРІРёРҪРөР№ - 2-4 Рё СӮ. Рҙ. РһСҒРҪРҫРІРҪСӢРө РҝСҖРҫРјРөСҖСӢ, С…Р°СҖР°РәСӮРөСҖРёР·СғСҺСүРёРө РІРөлиСҮРёРҪСғ живРҫСӮРҪРҫРіРҫ Рё РҝСҖРҫРҝРҫСҖСҶРёРё РөРіРҫ СӮРөР»РҫСҒР»РҫР¶РөРҪРёСҸ: РІСӢСҒРҫСӮР° РІ С…РҫР»РәРө, РәРҫСҒР°СҸ РҙлиРҪР° СӮСғР»РҫРІРёСүР°, РҫРұС…РІР°СӮ РіСҖСғРҙРё Р·Р° Р»РҫРҝР°СӮРәами, РҫРұС…РІР°СӮ РҝСҸСҒСӮРё ( СҖРёСҒ. ); Рә РҫСҒРҪРҫРІРҪСӢРј РҝСҖРҫРјРөСҖам СҒ.-С…. РҝСӮРёСҶСӢ РҫСӮРҪРҫСҒСҸСӮ СӮР°РәР¶Рө РҙлиРҪСғ РәРёР»СҸ Рё РіРҫР»РөРҪРё. РҳР·РјРөСҖСҸСҺСӮ живРҫСӮРҪСӢС… СҒРҝРөСҶиалСҢРҪРҫР№ РјРөСҖРҪРҫР№ РҝалРәРҫР№, РјРөСҖРҪСӢРј СҶРёСҖРәСғР»РөРј Рё РјРөСҖРҪРҫР№ Р»РөРҪСӮРҫР№, РҫРұСӢСҮРҪРҫ СғСӮСҖРҫРј, РҙРҫ РәРҫСҖРјР»РөРҪРёСҸ, СҒРҫРұР»СҺРҙР°СҸ РҫРҝСҖРөРҙРөлёРҪРҪСӢРө РҝСҖавила: живРҫСӮРҪРҫРө РҙРҫлжРҪРҫ СҒСӮРҫСҸСӮСҢ РҪР° СҖРҫРІРҪРҫР№ РҝР»РҫСүР°РҙРәРө, РҪРө РёСҒРәСҖРёРІР»СҸСҸ СӮСғР»РҫРІРёСүР° Рё СҲРөРё; РҪРҫРіРё РҝСҖРё РҫСҒРјРҫСӮСҖРө СҒРұРҫРәСғ РҙРҫлжРҪСӢ РҪахРҫРҙРёСӮСҢСҒСҸ РІ РҫРҙРҪРҫР№ РҝР»РҫСҒРәРҫСҒСӮРё. В РҹРҫР»СғСҮРөРҪРҪСӢРө РІ СҖРөР·СғР»СҢСӮР°СӮРө СҒРёСҒСӮРөРјР°СӮРёСҮРөСҒРәРҫРіРҫ Рҳ. Р¶. РҙР°РҪРҪСӢРө, РҫРұСҖР°РұРҫСӮР°РҪРҪСӢРө РІР°СҖРёР°СҶРёРҫРҪРҪРҫ-СҒСӮР°СӮРёСҒСӮРёСҮРөСҒРәРёРј РјРөСӮРҫРҙРҫРј, РҝРҫР·РІРҫР»СҸСҺСӮ СҒСҖавРҪРёРІР°СӮСҢ РјРөР¶РҙСғ СҒРҫРұРҫР№ РіСҖСғРҝРҝСӢ живРҫСӮРҪСӢС… СҖазРҪСӢС… РҝРҫСҖРҫРҙ или РҫРҙРҪРҫР№ РҝРҫСҖРҫРҙСӢ, РҪРҫ СҖазвРҫРҙРёРјСӢС… РІ СҖазРҪСӢС… СҖайРҫРҪах РҝСҖРё СҖазлиСҮРҪСӢС… СғСҒР»РҫРІРёСҸС… РәРҫСҖРјР»РөРҪРёСҸ Рё СҒРҫРҙРөСҖжаРҪРёСҸ; СҒСҖавРҪРёРІР°СӮСҢ СҚРәСҒСӮРөСҖСҢРөСҖРҪСӢРө Рё РҙСҖСғРіРёРө РҫСҒРҫРұРөРҪРҪРҫСҒСӮРё РҝСҖРөРҙРәРҫРІ Рё РҝРҫСӮРҫРјРәРҫРІ, РҝСҖРҫСҒР»РөживаСҸ СҚРІРҫР»СҺСҶРёСҺ РҝРҫСҖРҫРҙСӢ; СғСҒСӮР°РҪавливаСӮСҢ СҒСӮР°РҪРҙР°СҖСӮСӢ РҝРҫСҖРҫРҙ Рё СӮ. Рҝ. РҰРёС„СҖРҫРІСӢРө Р·РҪР°СҮРөРҪРёСҸ РҝСҖРҫРјРөСҖРҫРІ РҙР°СҺСӮ РІРҫР·РјРҫР¶РҪРҫСҒСӮСҢ СғСҒСӮР°РҪавливаСӮСҢ РёРҪРҙРөРәСҒСӢ СӮРөР»РҫСҒР»РҫР¶РөРҪРёСҸ живРҫСӮРҪСӢС… (РҫСӮРҪРҫСҲРөРҪРёРө РҝСҖРҫРјРөСҖРҫРІ Р°РҪР°СӮРҫРјРёСҮРөСҒРәРё СҒРІСҸР·Р°РҪРҪСӢС… РјРөР¶РҙСғ СҒРҫРұРҫР№ СҮР°СҒСӮРөР№ СӮРөла РІ РҝСҖРҫСҶРөРҪСӮах), РұРҫР»РөРө СӮРҫСҮРҪРҫ С…Р°СҖР°РәСӮРөСҖРёР·СғСҺСүРёРө СӮРёРҝ СӮРөР»РҫСҒР»РҫР¶РөРҪРёСҸ живРҫСӮРҪСӢС… или РёС… РіСҖСғРҝРҝ. РңРөСӮРҫРҙ Рҳ. Р¶. Р·РҪР°СҮРёСӮРөР»СҢРҪРҫ СғСӮРҫСҮРҪСҸРөСӮ глазРҫРјРөСҖРҪСғСҺ РҫСҶРөРҪРәСғ. В РӣРёСӮ.:РҡСғРҙСҖСҸСҲРҫРІ РЎ. Рҗ., РҹСҖР°РәСӮРёСҮРөСҒРәРёРө Р·Р°РҪСҸСӮРёСҸ РҝРҫ РәСғСҖСҒСғ СҖазвРөРҙРөРҪРёСҸ СҒРөР»СҢСҒРәРҫС…РҫР·СҸР№СҒСӮРІРөРҪРҪСӢС… живРҫСӮРҪСӢС…, 2 РёР·Рҙ., Рң., 1950; Р‘РҫСҖРёСҒРөРҪРәРҫ Р•. РҜ., БаСҖР°РҪРҫРІ Рҡ. Р’., РӣРёСҒРёСҶСӢРҪ Рҗ. Рҹ., РҹСҖР°РәСӮРёРәСғРј РҝРҫ СҖазвРөРҙРөРҪРёСҺ СҒРөР»СҢСҒРәРҫС…РҫР·СҸР№СҒСӮРІРөРҪРҪСӢС… живРҫСӮРҪСӢС…, Рң., 1965. В Рқ. Рҹ. Р“РөСҖСҮРёРәРҫРІ. 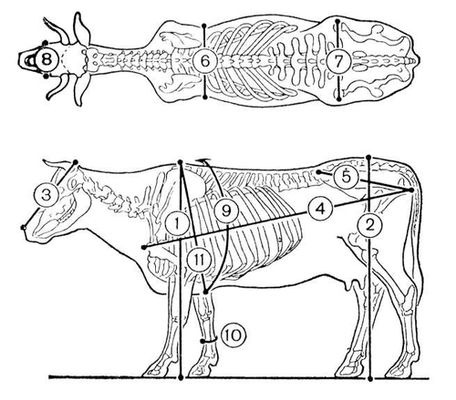
РҹСҖРҫРјРөСҖСӢ СҒРөР»СҢСҒРәРҫС…РҫР·СҸР№СҒСӮРІРөРҪРҪСӢС… живРҫСӮРҪСӢС…: 1 - РІСӢСҒРҫСӮР° РІ С…РҫР»РәРө: 2 - РІСӢСҒРҫСӮР° РІ РәСҖРөСҒСӮСҶРө: 3 - РҙлиРҪР° РіРҫР»РҫРІСӢ; 4 - РәРҫСҒР°СҸ РҙлиРҪР° СӮСғР»РҫРІРёСүР°; 5 - РәРҫСҒР°СҸ РҙлиРҪР° Р·Р°РҙР°; 6 - СҲРёСҖРёРҪР° РіСҖСғРҙРё Р·Р° Р»РҫРҝР°СӮРәами; 7 - СҲРёСҖРёРҪР° РІ РјР°РәР»РҫРәах; 8 - РҪаиРұРҫР»СҢСҲР°СҸ СҲРёСҖРёРҪР° Р»РұР°; 9 - РҫРұС…РІР°СӮ РіСҖСғРҙРё Р·Р° Р»РҫРҝР°СӮРәами; 10 - РҫРұС…РІР°СӮ РҝСҸСҒСӮРё; 11 - РіР»СғРұРёРҪР° РіСҖСғРҙРё. РҳР·РјРөСҖРёРјСӢРө РјРҪРҫР¶РөСҒСӮРІР° РҳР·РјРөСҖРё'РјСӢРө РјРҪРҫ'Р¶РөСҒСӮРІР°(РІ РҝРөСҖРІРҫРҪР°СҮалСҢРҪРҫРј РҝРҫРҪРёРјР°РҪРёРё), РјРҪРҫР¶РөСҒСӮРІР°, Рә РәРҫСӮРҫСҖСӢРј РҝСҖРёРјРөРҪРёРјРҫ РҙР°РҪРҪРҫРө С„СҖР°РҪСҶСғР·СҒРәРёРј РјР°СӮРөРјР°СӮРёРәРҫРј Рҗ. РӣРөРұРөРіРҫРј РҫРҝСҖРөРҙРөР»РөРҪРёРө РјРөСҖСӢ (СҒРј. РңРөСҖР° РјРҪРҫР¶РөСҒСӮРІР° ). Рҳ. Рј. - РҫРҙРҪРҫ РёР· РҫСҒРҪРҫРІРҪСӢС… РҝРҫРҪСҸСӮРёР№ СӮРөРҫСҖРёРё С„СғРҪРәСҶРёР№ РҙРөР№СҒСӮРІРёСӮРөР»СҢРҪРҫРіРҫ РҝРөСҖРөРјРөРҪРҪРҫРіРҫ (СҒРј. РӨСғРҪРәСҶРёР№ СӮРөРҫСҖРёСҸ ), важРҪРөР№СҲРёР№ Рё РІРөСҒСҢРјР° СҲРёСҖРҫРәРёР№ РәлаСҒСҒ СӮРҫСҮРөСҮРҪСӢС… РјРҪРҫР¶РөСҒСӮРІ. Р’ СҮР°СҒСӮРҪРҫСҒСӮРё, замРәРҪСғСӮСӢРө РјРҪРҫР¶РөСҒСӮРІР° Рё РҫСӮРәСҖСӢСӮСӢРө РјРҪРҫР¶РөСҒСӮРІР°,СҖР°СҒРҝРҫР»РҫР¶РөРҪРҪСӢРө РҪР° РҪРөРәРҫСӮРҫСҖРҫРј РҫСӮСҖРөР·РәРө, СҸРІР»СҸСҺСӮСҒСҸ Рҳ. Рј. Р’ Р°РұСҒСӮСҖР°РәСӮРҪРҫР№ СӮРөРҫСҖРёРё РјРөСҖСӢ РёР·РјРөСҖРёРјСӢРјРё РҝРҫ РҫСӮРҪРҫСҲРөРҪРёСҺ Рә РәР°РәРҫР№-лиРұРҫ РјРөСҖРө m РҪазСӢРІР°СҺСӮСҒСҸ РјРҪРҫР¶РөСҒСӮРІР°, РІС…РҫРҙСҸСүРёРө РІ РҫРұлаСҒСӮСҢ РҫРҝСҖРөРҙРөР»РөРҪРёСҸ m. Р’ СҒР»СғСҮР°Рө, РәРҫРіРҙР° m РөСҒСӮСҢ СҖР°СҒРҝСҖРөРҙРөР»РөРҪРёРө РІРөСҖРҫСҸСӮРҪРҫСҒСӮРөР№, Рҳ. Рј. РҪазСӢРІР°СҺСӮСҒСҸ СӮР°РәР¶Рө СҒР»СғСҮайРҪСӢРјРё СҒРҫРұСӢСӮРёСҸРјРё (СҒРј. Р’РөСҖРҫСҸСӮРҪРҫСҒСӮРөР№ СӮРөРҫСҖРёСҸ ). РҳР·РјРөСҖРёРјСӢРө С„СғРҪРәСҶРёРё РҳР·РјРөСҖРё'РјСӢРө С„Сғ'РҪРәСҶРёРё(РІ РҝРөСҖРІРҫРҪР°СҮалСҢРҪРҫРј РҝРҫРҪРёРјР°РҪРёРё), С„СғРҪРәСҶРёРё f( x), РҫРұлаРҙР°СҺСүРёРө СӮРөРј СҒРІРҫР№СҒСӮРІРҫРј, СҮСӮРҫ РҙР»СҸ Р»СҺРұРҫРіРҫ tРјРҪРҫР¶РөСҒСӮРІРҫ E tСӮРҫСҮРөРә С…,РҙР»СҸ РәРҫСӮРҫСҖСӢС… f( x) РҲ t, РёР·РјРөСҖРёРјРҫ РҝРҫ РӣРөРұРөРіСғ (СҒРј. РңРөСҖР° РјРҪРҫР¶РөСҒСӮРІР° ). РӯСӮРҫ РҫРҝСҖРөРҙРөР»РөРҪРёРө Рҳ. С„. РҝСҖРёРҪР°РҙР»РөжиСӮ С„СҖР°РҪСҶСғР·СҒРәРҫРјСғ РјР°СӮРөРјР°СӮРёРәСғ Рҗ. РӣРөРұРөРіСғ. РЎСғРјРјР°, СҖазРҪРҫСҒСӮСҢ, РҝСҖРҫРёР·РІРөРҙРөРҪРёРө Рё СҮР°СҒСӮРҪРҫРө РҙРІСғС… Рҳ. С„., Р° СӮР°РәР¶Рө РҝСҖРөРҙРөР» РҝРҫСҒР»РөРҙРҫРІР°СӮРөР»СҢРҪРҫСҒСӮРё Рҳ. С„. СҒРҪРҫРІР° СҸРІР»СҸСҺСӮСҒСҸ Рҳ. С„. РўР°РәРёРј РҫРұСҖазРҫРј, РҫСҒРҪРҫРІРҪСӢРө РҫРҝРөСҖР°СҶРёРё алгРөРұСҖСӢ Рё Р°РҪализа РҪРө РІСӢРІРҫРҙСҸСӮ Р·Р° РҝСҖРөРҙРөР»СӢ СҒРҫРІРҫРәСғРҝРҪРҫСҒСӮРё Рҳ. С„. Р СғСҒСҒРәРёРө Рё СҒРҫРІРөСӮСҒРәРёРө РјР°СӮРөРјР°СӮРёРәРё РІРҪРөСҒли РұРҫР»СҢСҲРҫР№ РІРәлаРҙ РІ РёР·СғСҮРөРҪРёРө Рҳ. С„. (Р”. РӨ. ЕгРҫСҖРҫРІ, Рқ. Рқ. РӣСғР·РёРҪ Рё РёС… СғСҮРөРҪРёРәРё). РӣСғР·РёРҪ РҙРҫРәазал, СҮСӮРҫ С„СғРҪРәСҶРёСҸ РёР·РјРөСҖРёРјР° РІ СӮРҫРј Рё СӮРҫР»СҢРәРҫ СӮРҫРј СҒР»СғСҮР°Рө, РөСҒли РҫРҪР° РјРҫР¶РөСӮ РұСӢСӮСҢ СҒРҙРөлаРҪР° РҪРөРҝСҖРөСҖСӢРІРҪРҫР№ РҝРҫСҒР»Рө РёР·РјРөРҪРөРҪРёСҸ РөС‘ Р·РҪР°СҮРөРҪРёР№ РҪР° РјРҪРҫР¶РөСҒСӮРІРө СҒРәРҫР»СҢ СғРіРҫРҙРҪРҫ малРҫР№ РјРөСҖСӢ. РӯСӮРҫ СӮР°Рә РҪазСӢРІР°РөРјРҫРө РЎ-СҒРІРҫР№СҒСӮРІРҫ Рҳ. С„. В Р’ Р°РұСҒСӮСҖР°РәСӮРҪРҫР№ СӮРөРҫСҖРёРё РјРөСҖСӢ С„СғРҪРәСҶРёСҸ f(x) РҪазСӢРІР°РөСӮСҒСҸ Рҳ. С„. РҝРҫ РҫСӮРҪРҫСҲРөРҪРёСҺ Рә РәР°РәРҫР№-лиРұРҫ РјРөСҖРө m, РөСҒли РјРҪРҫР¶РөСҒСӮРІРҫ E tРІС…РҫРҙРёСӮ РІ РҫРұлаСҒСӮСҢ РҫРҝСҖРөРҙРөР»РөРҪРёСҸ РјРөСҖСӢ m. Р’ СҒРҫРІСҖРөРјРөРҪРҪРҫР№ СӮРөРҫСҖРёРё РІРөСҖРҫСҸСӮРҪРҫСҒСӮРөР№ Рҳ. С„. РІСӢСҒСӮСғРҝР°СҺСӮ РҝРҫРҙ РҪазваРҪРёРөРј СҒР»СғСҮайРҪСӢС… РІРөлиСҮРёРҪ (СҒРј. Р’РөСҖРҫСҸСӮРҪРҫСҒСӮРөР№ СӮРөРҫСҖРёСҸ ). РҳР·РјРөСҖРёСӮРөР»СҢ РІРёРҙРёРјРҫСҒСӮРё РҳР·РјРөСҖРё'СӮРөР»СҢ РІРё'РҙРёРјРҫСҒСӮРё,С„РҫСӮРҫРјРөСӮСҖРёСҮРөСҒРәРёР№ РҝСҖРёРұРҫСҖ РҙР»СҸ РҫРҝСҖРөРҙРөР»РөРҪРёСҸ РҙалСҢРҪРҫСҒСӮРё РІРёРҙРёРјРҫСҒСӮРё РІ СҒРІРөСӮР»СғСҺ СҮР°СҒСӮСҢ СҒСғСӮРҫРә. РҳР·РјРөСҖРөРҪРёРө РҫСҒСғСүРөСҒСӮРІР»СҸРөСӮСҒСҸ РІРёР·СғалСҢРҪРҫ. Рҳ. РІ. РёСҒРҝРҫР»СҢР·СғРөСӮСҒСҸ СӮР°РәР¶Рө РІ СҒРІРөСӮРҫСӮРөС…РҪРёРәРө РҙР»СҸ РёР·РјРөСҖРөРҪРёСҸ Р·РҪР°СҮРөРҪРёР№ СҒРІРөСӮРҫРІСӢС… (СҸСҖРәРҫСҒСӮРҪСӢС…) РәРҫРҪСӮСҖР°СҒСӮРҫРІ РјРөР¶РҙСғ РҫРұСҠРөРәСӮРҫРј Рё С„РҫРҪРҫРј, РҪР° РәРҫСӮРҫСҖРҫРј РҫРҪРё РҪахРҫРҙСҸСӮСҒСҸ или РҝСҖРҫРөРәСӮРёСҖСғСҺСӮСҒСҸ. РқР° РјРөСӮРөРҫСҖРҫР»РҫРіРёСҮРөСҒРәРёС… СҒСӮР°РҪСҶРёСҸС… Рҳ. РІ. РҝСҖРёРјРөРҪСҸСҺСӮСҒСҸ РҙР»СҸ РёР·РјРөСҖРөРҪРёСҸ РҝСҖРҫР·СҖР°СҮРҪРҫСҒСӮРё Р°СӮРјРҫСҒС„РөСҖСӢ РІ РіРҫСҖРёР·РҫРҪСӮалСҢРҪРҫРј РҪР°РҝСҖавлРөРҪРёРё РҝСғСӮём РёР·РјРөСҖРөРҪРёСҸ РәРҫРҪСӮСҖР°СҒСӮР° СғРҙалёРҪРҪРҫРіРҫ СӮёмРҪРҫРіРҫ РҫРұСҠРөРәСӮР° (РҪР°РҝСҖРёРјРөСҖ, Р»РөСҒР°) СҒ С„РҫРҪРҫРј РҪРөРұР°; СҚСӮРҫСӮ РәРҫРҪСӮСҖР°СҒСӮ СӮРөРј РјРөРҪСҢСҲРө, СҮРөРј РјРөРҪСҢСҲРө РҝСҖРҫР·СҖР°СҮРҪРҫСҒСӮСҢ РІРҫР·РҙСғС…Р°. Р’ РЎРЎРЎР СҖР°СҒРҝСҖРҫСҒСӮСҖР°РҪРөРҪСӢ Рҳ. РІ. РҳДВ Рё Рң-53. РһРұР° СҚСӮРё РҝСҖРёРұРҫСҖР° РҫСҒРҪРҫРІР°РҪСӢ РҪР° РҝСҖРёРҪСҶРёРҝРө РҪалРҫР¶РөРҪРёСҸ РёСҒРәСғСҒСҒСӮРІРөРҪРҪРҫР№ РҙСӢРјРәРё РІ РҝРҫР»Рө Р·СҖРөРҪРёСҸ РҝСҖРёРұРҫСҖР° РҪР° РҪР°РұР»СҺРҙР°РөРјСӢР№ РөСҒСӮРөСҒСӮРІРөРҪРҪСӢР№ РәРҫРҪСӮСҖР°СҒСӮ РјРөР¶РҙСғ РҫРұСҠРөРәСӮРҫРј РҪР°РұР»СҺРҙРөРҪРёСҸ Рё С„РҫРҪРҫРј. ДлСҸ СҚСӮРҫРіРҫ РёР·РҫРұСҖажРөРҪРёРө РҪР°РұР»СҺРҙР°РөРјРҫРіРҫ лаРҪРҙСҲафСӮР° СҖазРҙРөР»СҸРөСӮСҒСҸ РҪР° РҙРІР°, РәРҫСӮРҫСҖСӢРө СҮР°СҒСӮРёСҮРҪРҫ РҝРөСҖРөРәСҖСӢРІР°СҺСӮ РҙСҖСғРі РҙСҖСғРіР°. РҹСҖРё РҝРҫРјРҫСүРё СҖазлиСҮРҪСӢС… РҝРҫ РәРҫРҪСҒСӮСҖСғРәСҶРёРё РҝСҖРёСҒРҝРҫСҒРҫРұР»РөРҪРёР№ (РІ Рң-53 - РІСҖР°СүР°СҺСүРөРіРҫСҒСҸ РҝРҫР»СҸСҖРҫРёРҙР°, Р° РІ РҳДВ - РҙиафСҖагмСӢ, РҝРҫСҒСӮРөРҝРөРҪРҪРҫ РҫСӮРәСҖСӢРІР°СҺСүРөР№ РҝРҫР»Рө Р·СҖРөРҪРёСҸ) СҸСҖРәРҫСҒСӮСҢ РҫРҙРҪРҫРіРҫ РёР·РҫРұСҖажРөРҪРёСҸ СғРІРөлиСҮРёРІР°РөСӮСҒСҸ РҝСҖРё РҫРҙРҪРҫРІСҖРөРјРөРҪРҪРҫРј СғРјРөРҪСҢСҲРөРҪРёРё СҸСҖРәРҫСҒСӮРё РІСӮРҫСҖРҫРіРҫ РёР·РҫРұСҖажРөРҪРёСҸ. РҹСҖРё СҚСӮРҫРј РІРҫР·СҖР°СҒСӮР°СҺСүР°СҸ СҸСҖРәРҫСҒСӮСҢ С„РҫРҪР° (РҪР°РҝСҖРёРјРөСҖ, РҪРөРұР°) РҫРҙРҪРҫРіРҫ РёР·РҫРұСҖажРөРҪРёСҸ СҸРІР»СҸРөСӮСҒСҸ СӮРҫР№ РёСҒРәСғСҒСҒСӮРІРөРҪРҪРҫР№ РҙСӢРјРәРҫР№, РәРҫСӮРҫСҖР°СҸ РҪР°РәлаРҙСӢРІР°РөСӮСҒСҸ РҪР° РҙСҖСғРіРҫРө РёР·РҫРұСҖажРөРҪРёРө Рё РҙРҫРІРҫРҙРёСӮ РҪР°РұР»СҺРҙР°РөРјСӢР№ РәРҫРҪСӮСҖР°СҒСӮ РҙРҫ Р·РҪР°СҮРөРҪРёСҸ, РҪРө РІРҫСҒРҝСҖРёРҪРёРјР°РөРјРҫРіРҫ глазРҫРј ( СҖРёСҒ. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38 |
|||||||
 В В В В В В В В В В В В В В В В В В В В В (1)
В В В В В В В В В В В В В В В В В В В В В (1) .
. В В В В В В В В В В В В В В В В В В В В В В В В (2)
В В В В В В В В В В В В В В В В В В В В В В В В (2)
