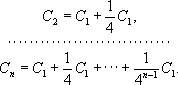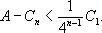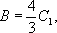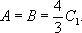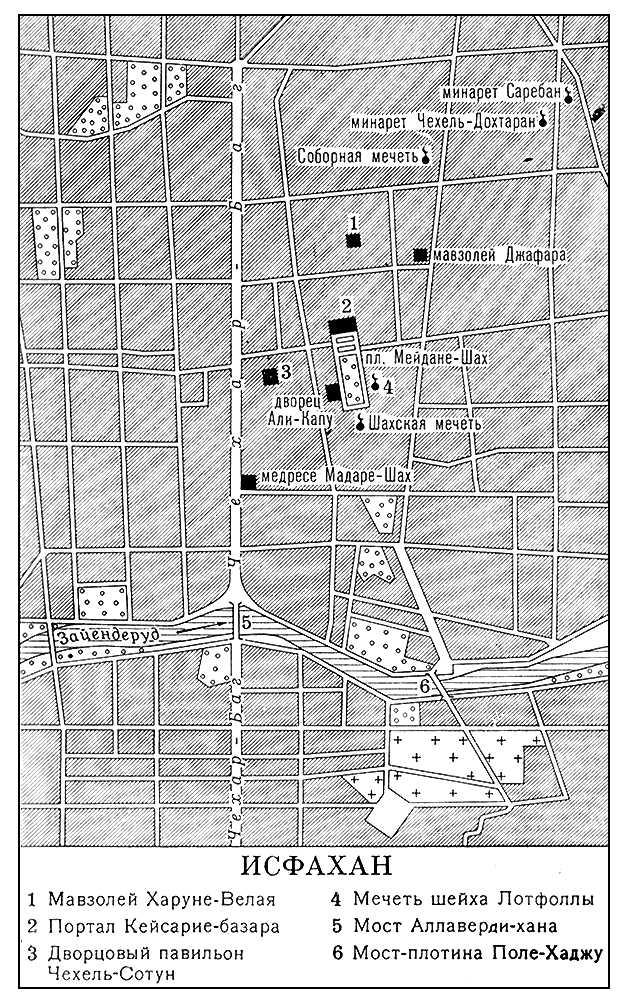
Исфаханская школа

Исфаха'нская шко'ламиниатюры, одна из основных школ иранской миниатюры, сформировавшаяся на рубеже 16-17 вв. при дворе шаха Аббаса I в г. Исфахан. В И. ш. наряду с книжной иллюстрацией широко распространяются портретные и жанровые миниатюры на отдельных листах, собираемых в альбомы. Миниатюры И. ш. в значительной мере утратили многоцветную красочность и подчёркнутую плоскостность, характерные для всей предшествующей иранской миниатюры. Основное значение получил виртуозный рисунок, исполненный свободными мазками кисти, с лёгкой подцветкой, и придающий фигурам объёмность и живость движения. Вместе с тем в миниатюре И. ш. сохранились традиционные черты: тончайшая разработка деталей, широкое использование золота в изображении фона и в орнаменте одежд. Становление стиля И. ш. связано с творчеством её крупнейшего представителя Реза Аббаси. В миниатюрах художников середины и 2-й половины 17 в. (Мохаммед Касим, Афзаль оль-Хосейни, Мохаммед Юсуф, Мохаммед Али, Моин Мосаввер) фигуры становятся крупнее, пейзаж получает более реалистическую трактовку. В 1670-е гг. появилось направление, сложившееся под влиянием европейской живописи. Его представители (художники Мохаммед Заман, Али-Кули-бек, Джабадар и др.) в своих произведениях, нередко на темы христианской мифологии, применяли светотеневую моделировку лиц и одежд, линейную и воздушную перспективу в изображении пейзажных фонов. К началу 18 в. это «европеизирующее» направление становится преобладающим.

  Лит.:Денике Б., Живопись Ирана, М., 1938; Персидские миниатюры 14-17 вв. [Альбом]. Вступит. статья О. Ф. Акимушкина и А. А. Иванова, М., 1968; Stchoukine J., Les peintures des manuscrites de Shah Abbas 1-er б la fin des Safavis, P., 1964.

  А. Т. Адамова.

Мохаммед Заман. «Бахрам Гур и дракон». 1675-76. Британский музей. Лондон.

Реза Аббаси. «Пастух». 1634. Публичная библиотека им. М. Е. Салтыкова-Щедрина. Ленинград.

Исхак Ахмет Абдуллович

Исха'к(Исхаков) Ахмет Абдуллович [р. 18.4(1.5).1905, Казань], татарский советский поэт. Член КПСС с 1945. Родился в семье служащего. Работал журналистом (1925-39). Участник Великой Отечественной войны 1941-45. Печатается с 1923. Первый сборник «Песни каменных улиц» вышел в 1928. Основные темы поэзии И. - величие Советской родины, дружба народов, борьба за мир. Лирика и поэмы военных лет («Клятва», «Песня о герое-танкисте Петре Новикове») глубоко патриотичны, мужественны. В цикле стихов «Заря над Азией» (1953) воспел борьбу народов против колониального гнёта. И. - автор сатирического сборника «Анкета для влюблённой» (1966, на русском языке). Переводил на татарский язык произведения А. С. Пушкина, М. Ю. Лермонтова, В. В. Маяковского, Т. Г. Шевченко, Навои и др. Награжден орденом Трудового Красного Знамени.

  Соч.: Сайланма эсэрлэр, Казан, 1965; в рус. пер. - Стихи, Каз., 1956; Встреча в песне, М., 1960.

  Лит.:Хэким С., «Курай», «Совет эдэбияты», 1946, № 11-12.

Исход

Исхо'д,вторая книга Пятикнижия .

Исходные геодезические даты

Исхо'дные геодези'ческие да'ты,совокупность величин, определяющих положение референц-эллипсоида , принятого для обработки геодезической сети какой-либо страны или группы стран, относительно геоида , т. е. величин, фиксирующих положение референц-эллипсоида в теле Земли. В состав И. г. д. входят геодезические координаты (см. Координаты в геодезии), а именно широта B ₀и долгота L ₀одного из опорных пунктов сети, принятого за исходный, геодезический азимут A ₀направления с исходного пункта на один из смежных пунктов сети и высота x ₀исходного пункта над геоидом. И. г. д. устанавливаются после вывода референц-эллипсоида путём определения астрономических координат (j ₀, l ₀) (см. Географические координаты ) исходного пункта и астрономического азимута a указанного выше направления и освобождения их от влияния уклонений отвеса. Геодезические координаты всех остальных пунктов сети и азимуты получают затем путём вычислений на основании результатов геодезических измерений, приведённых к поверхности референц-эллипсоида. Геодезические координаты пунктов астрономо-геодезической сети СССР и некоторых других стран вычисляются на поверхности Красовского эллипсоида . Исходным пунктом геодезической сети СССР служит центр бывшего Круглого зала Пулковской астрономической обсерватории, для которого приняты следующие геодезические координаты: широта B ₀= 59°46ў18ўў, 55, долгота L ₀= 30°19ў42ўў,09, высота x ₀положена равной нулю. Вывод указанных И. г. д. СССР выполнили А. А. Изотов и М. С. Молоденский в 1942. Эти И. г. д., как и эллипсоид Красовского, приняты за основу единой государственной системы координат при производстве всех геодезических и картографических работ на территории СССР.

  С начала 60-х гг. 20 в. методы космической геодезии позволили на основе наблюдений искусственных спутников Земли получать параметры земного эллипсоида , представляющего Землю в целом, и развивать единую мировую геодезическую систему координат, связывающую воедино разрозненные астрономо-геодезические сети отдельных материков и стран. Это имеет большое научное и практическое значение для решения проблем геодезии и ряда смежных наук. Несвязанные до этого астрономо-геодезические сети, обработанные ранее при различных И. г. д. и на разных референц-эллипсоидах, могут быть теперь отнесены к единой мировой геодезической системе координат на одном эллипсоиде, наиболее подходящем к Земле как планете в целом, или к единой мировой системе прямоугольных декартовых координат.

  Лит.:Закатов П. С., Курс высшей геодезии, М., 1964; Изотов А. А., Новые исходные геодезические даты СССР, в кн.: Сборник научно-технических и производственных статей по геодезии, картографии, топографии, аэросъёмке и гравиметрии, в. 17, М., 1948; Стандартная Земля. Геодезические параметры Земли на 1966 год. [Сб. ст.], пер. с англ., М., 1969.

  Г. А. Мещеряков.

Исчерпывания метод

Исче'рпывания ме'тод,метод доказательства, применявшийся математиками древности при нахождении площадей и объёмов. Название «метод исчерпывания» введено в 17 в.

  Типичная схема доказательства при помощи И. м. может быть изложена в современных обозначениях так: для определения величины Астроится некоторая последовательность величин C ₁, C ₂, ..., C _n,... так, что

C _n< A;                                                             (1)

предполагают также известным такое В, что

C _n < В                                                              (2)

и при любом целом Кдля достаточно больших nудовлетворяются неравенства

К( A- C _n) < D, К( В- C _n) < D,                         (3)

где D- постоянно. С современной точки зрения, для перехода от неравенств (3) к равенству

А= В                                                                (4)

достаточно заметить, что из условий (1), (2) и (3) следует

Математики древности, не располагавшие теорией пределов , обращались к доказательству от противного и доказывали невозможность каждого из неравенств А< В, В< А. Чтобы опровергнуть первое из них, при помощи аксиомы Евдокса - Архимеда (см. Архимеда аксиома ) устанавливали, что для R= B - Асуществует такое К, что KR> Dи в силу условия (1) получали

К( В- C _n) > К( В- A) > D,

что противоречит второму из неравенств (3). Аналогично опровергалось другое предположение. После этого оставалось принять только равенство (4).

  Введение И. м. вместе с лежащей в его основе аксиомой приписывается Евдоксу Книдскому. Этим методом широко пользовался Евклид, а с особенным искусством и разнообразием - Архимед. Например, для определения площади сегмента Апараболы Архимед строит площади C ₁, C ₂, ..., «исчерпывающие» при их постепенном нарастании площадь Aсегмента, по схеме, ясной из чертежа. При этом

Вместо того чтобы прибегнуть к предельному переходу,

Архимед геометрически доказывает, что при любом n

Вводя площадь

Архимед получает, что

и, следуя изложенному выше порядку, заканчивает доказательство того, что

Рис. к ст. Исчерпывания метод.

Исчисление

Исчисле'ние,основанный на чётко сформулированных правилах формальный аппарат оперирования со знаками определённого вида, позволяющий дать исчерпывающе точное описание некоторого класса задач, а для некоторых подклассов этого класса (лишь для наиболее простых И., совпадающих с ним) - и алгоритмы решения. Примерами И. могут служить совокупность арифметических правил оперирования с цифрами (т. е. числовыми знаками), «буквенное» И. элементарной алгебры, дифференциальное И., интегральное И., вариационное И. и другие ветви математического анализа и теории функций. Несмотря на раннее происхождение, термин «И.» употреблялся в математике до недавнего времени без строгого общего определения. С развитием математической логики возникла потребность в общей теории И. и в уточнении самого понятия «И.», которое подверглось более последовательной формализации. В большинстве случаев, однако, оказывается достаточным следующее (идущее от Д. Гильберта ) представление об И. Рассматривается некоторый (вообще говоря, бесконечный, хотя и, быть может, задаваемый посредством конечного числа символов) алфавит, из элементов которого, именуемых буквами, с помощью четко сформулированных правил образования строятся формулы рассматриваемого И. (называемые также иногда словами, или выражениями). Некоторые из таких («правильно построенных») формул объявляются аксиомами, а из них с помощью правил преобразования (или, иначе, правил вывода) «выводятся» новые формулы, называемые теоремами данного И. Иногда термин «И.» относят лишь к «словарной» («выразительной») части описанного построения, говоря, что присоединение к ней «дедуктивной» части (т. е. добавление к алфавиту и правилам образования аксиом и правил ввода) даёт формальную систему. Впрочем, эти термины часто считают синонимичными (и в качестве синонимов пользуются также терминами «логистическая система», «формализм», «формальная теория» и многими др.). Если такое неинтерпретированное («бессмысленное») И. сопоставить с некоторой интерпретацией (или, как говорят, дополнить чисто синтаксические рассмотрения некоторой семантикой; см. Логическая семантика ) то получают формализованный язык . Представление содержательных логических (и логико-математических) теорий в виде формализованных языков есть характерная особенность математической логики (см. также Доказательство ).

  Лит.:Клини С. К., Введение в метаматематику, пер. с англ., М., 1957, § 14-20; Марков А. А., Теория алгорифмов, М.-Л., 1954 (Тр. Математического института им. В. А. Стеклова, т. 42); Карри Х. Б., Основания математической логики, пер. с англ., М., 1969, гл. 2; Математическая теория логического вывода, Сборник переводов, под ред. А. В. Идельсона, Г. Е. Минца, М., 1967; Логические и логико-математические исчисления, 1, Сб. работ, под ред. В. П. Оревкова, Л., 1968.

  Ю. Л. Гастев.

Исчисление высказываний

Исчисле'ние выска'зываний,исчисление суждений, раздел математической логики , в котором формально-аксиоматическим методом изучаются сложные (составные) высказывания, составленные из простых (элементарных, не анализируемых) высказываний с помощью логических связок «и», «или», «если..., то» и «неверно, что». При этом ставится цель охарактеризовать общезначимые в том или ином смысле высказывательные формы, т. е. те формулы, которые при любой подстановке высказываний вместо переменных дают высказывания, верные в соответствующем смысле.

Исчисление предикатов

Исчисле'ние предика'тов,раздел математической логики - совокупность логико-математических исчислений , формализующих те разделы современной логики, в которых отображаются и изучаются (в связи с рассмотрением субъектно-предикатной структуры предложений) правила оперирования с кванторами . См. Высказывание , Логика предикатов .