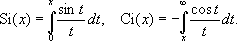|
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (ИН)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ИН) - Чтение (стр. 42)
Трудность И. и. по сравнению с дифференциальным исчислением заключается в том, что интегралы от элементарных функций не всегда выражаются через элементарные, могут не выражаться, как говорят, «в конечном виде». И. и. располагает лишь отдельными приёмами интегрирования в конечном виде, область применения каждого из которых ограничена (способы интегрирования излагаются в учебниках математического анализа: обширные таблицы интегралов приводятся во многих справочниках). К классу функций, интегралы от которых всегда выражаются в элементарных функциях, принадлежит множество всех рациональных функций
где P( x) и Q( x) - многочлены. Многие функции, не являющиеся рациональными, также интегрируются в конечном виде, например функции, рационально зависящие от
или же от xи рациональных степеней дроби
В конечном виде интегрируются и многие трансцендентные функции, например рациональные функции синуса и косинуса. Функции, которые изображаются неопределёнными интегралами, не берущимися в конечном виде, представляют собой новые трансцендентные функции. Многие из них хорошо изучены (см., например, Интегральный логарифм , Интегральный синус и интегральный косинус , Интегральная показательная функция ). Понятие интеграла распространяется на функции многих действительных переменных (см. Кратный интеграл , Криволинейный интеграл , Поверхностный интеграл ), а также на функции комплексного переменного (см. Аналитические функции ) и вектор-функции (см. Векторное исчисление ). О расширении и обобщении понятия интеграла см. ст. Интеграл. Историческая справка.Возникновение задач И. и. связано с нахождением площадей и объёмов. Ряд задач такого рода был решен математиками Древней Греции. Античная математика предвосхитила идеи И. и. в значительно большей степени, чем дифференциального исчисления. Большую роль при решении таких задач играл исчерпывания метод , созданный Евдоксом Книдским и широко применявшийся Архимедом.Однако Архимед не выделил общего содержания интеграционных приёмов и понятия об интеграле, а тем более не создал алгоритма И. и. Учёные Среднего и Ближнего Востока в 9-15 вв. изучали и переводили труды Архимеда на общедоступный в их среде арабский язык, но существенно новых результатов в И. и. они не получили. Деятельность европейских учёных в это время была ещё более скромной. Лишь в 16 и 17 вв. развитие естественных наук поставило перед математикой Европы ряд новых задач, в частности задачи на нахождения квадратур, кубатур и определение центров тяжести. Труды Архимеда, впервые изданные в 1544 (на латинском и греческом языках), стали привлекать широкое внимание, и их изучение явилось одним из важнейших отправных пунктов дальнейшего развития И. и. Античный «неделимых» метод был возрожден И. Кеплером.В более общей форме идеи этого метода были развиты Б. Кавальери , Э. Торричелли , Дж. Валлисом , Б. Паскалем.Методом «неделимых» был решен ряд геометрических и механических задач. К этому же времени относятся опубликованные позднее работы П. Ферма по квадрированию парабол n-й степени, а затем - работы Х. Гюйгенса по спрямлению кривых. В итоге этих исследований выявилась общность приёмов интегрирования при решении внешне несходных задач геометрии и механики, приводившихся к квадратурам как к геометрическому эквиваленту определённого интеграла. Заключительным звеном в цепи открытий этого периода было установление взаимно обратной связи между задачами на проведение касательной и на квадратуры, т. е. между дифференцированием и интегрированием. Основные понятия и алгоритм И. и. были созданы независимо друг от друга И. Ньютоном и Г. Лейбницем.Последнему принадлежит термин «интегральное исчисление» и обозначение интеграла т ydx. При этом в работах Ньютона основную роль играло понятие неопределённого интеграла (флюенты, см. Флюксий исчисление ), тогда как Лейбниц исходил из понятия определённого интеграла. Дальнейшее развитие И. и. в 18 в. связано с именами И. Бернулли и особенно Л. Эйлера.В начале 19 в. И. и. вместе с дифференциальным исчислением было перестроено О. Коши на основе теории пределов. В развитии И. и. в 19 в. приняли участие русские математики М. В. Остроградский , В. Я. Буняковский , П. Л. Чебышев . В конце 19 - начале 20 вв. развитие теории множеств и теории функций действительного переменного привело к углублению и обобщению основных понятий И. и. (Б. Риман , А. Лебег и др.). Лит.: История.Ван дер Варден Б. Л., Пробуждающаяся наука, пер. с голл., М., 1959; Вилейтнер Г., История математики от Декарта до середины 19 столетия, пер. с нем., 2 изд., М., 1966; Строек Д. Я., Краткий очерк истории математики, пер. с нем., 2 изд., М., 1969; Cantor М.. Vorleslingen ьber Geschichte der Mathematik, 2 Aufl., Bd 3-4, Lpz. - B., 1901-24. Работы основоположников и классиков И. и.Ньютон И., Математические работы, пер. с латин., М.-Л., 1937; Лейбниц Г., Избранные отрывки из математических сочинений, пер. с. латин., «Успехи математических наук», 1948, т. 3, в. 1; Эйлер Л., Интегральное исчисление, пер. с латин., тт. 1-3, М., 1956-58; Коши О. Л., Краткое изложение уроков о дифференциальном и интегральном исчислении, пер. с франц., СПБ, 1831; его же, Алгебраический анализ, пер. с франц., Лейпциг, 1864. Учебники и учебные пособия по И. и.Хинчин Д. Я., Краткий курс математического анализа, 3 изд., 1957; Смирнов В. И., Курс высшей математики, 22 изд., т. 1, М., 1967; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969; Ильин В., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971; Курант Р., Курс дифференциального и интегрального исчисления, пер. с нем. и англ., 4 изд., т. 1, М., 1967; Двайт Г.-Б., Таблицы интегралов и другие математические формулы, пер. с англ., М., 1964. Под редакцией академика А. Н. Колмогорова. 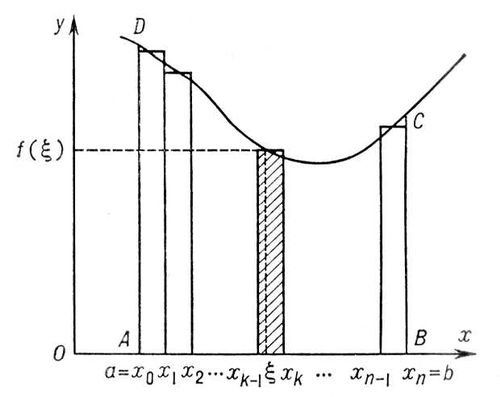
Рис. к ст. Интегральное исчисление. Интегральное стереокино Интегра'льное стереокино',стереоскопическое кино, в котором объёмно-пространственный образ создаётся в результате одновременной проекции на растровый экран не двух, как в однопарном стереоскопическом кино, а многих плоских взаимосвязанных между собой изображений (кадров), хотя зритель видит из них в каждое мгновение только 2 изображения: одно - левым, а другое - правым глазом. Метод И. с. впервые в мире был предложен в 1962-63 советским изобретателем безочкового стереоскопического кино С. П. Ивановым и совершенствовался им в последующие годы. В 1965 был продемонстрирован экспериментальный кинофильм (режиссер Н. В. Экк), снятый интегральным методом, а в 1972 в Москве (кинотеатр «Октябрь») впервые демонстрировался короткометражный видовой кинофильм «По Южному берегу Крыма», снятый также интегральным методом (режиссёр и оператор Н. И. Большаков). При наиболее простом способе съёмки И. с. на 8-, 16- или 35- ммкиноплёнку применяется обычный (однообъективный) съёмочный аппарат с любыми объективами. В нём изменяется только рамка, ограничивающая поле зрения визира в соответствии с выбранным стереоскопическим экраном. Особенность процесса съёмки заключается в том, что съемочный аппарат устанавливается не обычно, а поворачивается вокруг оптической оси объектива на 90° для обеспечения горизонтального продвижения киноплёнки, необходимого при проекции, и перемещается в горизонтальной плоскости вокруг центрального объекта композиции ( рис. 1 ). Скорость перемещения камеры может быть рассчитана по формуле: v= LЧ K/10Чf ' c, где v- скорость движения камеры ( мм/сек), L- расстояние до центрального объекта композиции ( мм), К- частота смены кадров ( кадр/сек), f ' c-сопряжённое фокусное расстояние ( мм). По этой формуле могут быть составлены таблицы для наиболее характерных или часто встречающихся случаев съёмки. При съёмке допустимы 2-3-кратные отклонения от параметров, указанных в формуле. Простейший контроль правильности такой съёмки заключается в том, что видимые в визире перемещения самых ближних и самых удалённых объектов (относительно неподвижного центрального объекта) от одной границы кадра к другой должны происходить за время не более 10 секи не менее 2 сек. При проекции на растровый экран киноплёнка продвигается горизонтально с обычной частотой смены кадров (24 кадр/сек) мимо нескольких взаимосвязанных объективов. Количество объективов определяется оптическими параметрами растрового экрана. Так, при проекции на растровый экран с перспективным линзовым растром ( рис. 2 ) достаточно от 5 до 10 объективов. В этом случае на любое кресло зрительного зала придется от 5 до 10 элементарных взаимосвязанных фокальных зон, составляющих в целом интегральную зону стереоскопического видения (о фокальных зонах см. в ст. Стереоскопическое кино ). Посредством экрана образуется до 50 интегральных зон или 400-500 элементарных фокальных зон. Такое количество зон обеспечивает нормальные условия просмотра кинофильма зрителем: при отклонении зрителя вправо или влево стереоскопический эффект не пропадает, что неизбежно при однопарной безочковой стереоскопической проекции, а напротив, подчёркивается за счёт естественного перемещения ближних предметов относительно дальних, т. е. в полном соответствии с тем, что наблюдается в жизни. Однако рассмотренному способу получения И. с. свойствен недостаток: наиболее быстро движущиеся объекты оказываются заснятыми с большим временным параллаксом, проявляющимся при любой проекции в виде дробления изображения движущихся объектов; кроме того, при стереоскопической проекции наблюдается заметная деформация формы объектов и их пространственного положения. Во избежание этого явления предложено 2 более сложных способа получения И. с.: 1) увеличение при съёмке и проецировании частоты смены кадров в 2-4 раза; 2) съёмка и проецирование одновременно серии из 8-9 кадров при прежней частоте смены кадров. Для реализации последнего способа может быть использован киносъёмочный аппарат, в котором применена, например, перфорированная аэрофотоплёнка шириной 190 ммс поперечным (к вертикальному перемещению плёнки) размещением на ней серии из 9 отдельных взаимосвязанных кадров размером 19ґ19 ммкаждый. Лит.:Иванов Б. Т., Растровая стереоскопия в кино, М., 1945; Валюс Н. А., Растровая оптика, М., 1949; Иванов С.П., Иванов М. С., Быховский В. М. , Интегральная стереодиапроекция на ЭКСПО-70, «Техника кино и телевидения», 1970, № 10, с. 33-38. С. П. Иванов. 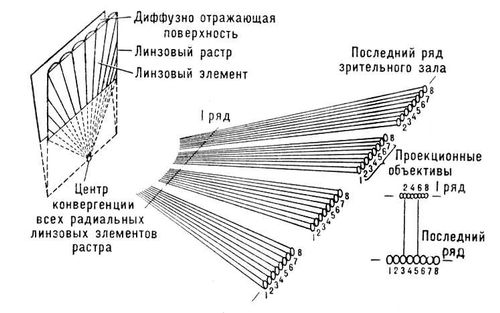
Рис. 2. Схема образования интегральных фокальных зон растровым экраном с перспективным растром. 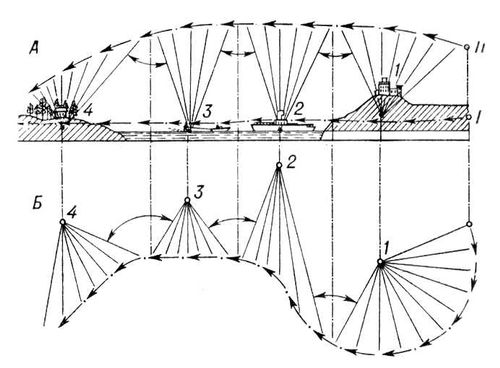
Рис. 1. Схема съёмки кинофильма интегральным методом: А - сверху вниз (в вертикальной плоскости); Б - в сторону (в горизонтальной плоскости); 1, 2, 3, 4 - центральные объекты композиции. Стрелками показаны пути перемещения съёмочного аппарата при съёмке в сторону (I) и сверху вниз (II); обоюдоострыми стрелками показан быстрый переход с одной визирной точки (центрального объекта) на другую. Интегральные уравнения Интегра'льные уравне'ния,уравнения, содержащие неизвестные функции под знаком интеграла. Многочисленные задачи физики и математической физики приводят к И. у. различных типов. Пусть, например, требуется с помощью некоторого оптического прибора получить изображение линейного объекта А, занимающего отрезок 0 Ј xЈ lоси Ox, причём освещённость объекта характеризуется плотностью u( x). Изображение Впредставляет собой некоторый отрезок другой оси x 1; последний путём подходящего выбора начала отсчёта и единицы длины также можно совместить с отрезком 0 Ј x 1 Ј l .Если дифференциально малый участок ( х, х+ D х) объекта Авызывает освещённость изображения Вс плотностью K( x 1, x) u( x) dx, где функция K( x 1 , x) определяется свойствами оптического прибора, то полная освещённость изображения будет иметь плотность
В зависимости от того, хотят ли добиться заданной освещённости v( x 1) изображения или «точного» фотографического изображения [ v( x) = ku( x), где постоянная kзаранее не фиксируется], или, наконец, определённой разницы освещённости Аи В[ u( x) - v( x) = f( x)], приходят к различным И. у. относительно функции u( x):
Вообще, линейным интегральным уравнением 1-го рода называется уравнение вида
линейным интегральным уравнением 2-го рода, или уравнением Фредгольма,-уравнение вида
[при f( x) є 0 оно называется однородным уравнением Фредгольма]; обычно рассматриваются уравнения Фредгольма с параметром l:
Во всех уравнениях функция
-так называемое ядро И. у. - известна, так же, как функция f( x) ( аЈ хЈ b); искомой является функция u( x) ( аЈ хЈ b). Функции K( x, y), f( x), u( x) и параметр уравнения l могут принимать как действительные, так и комплексные значения. В частном случае, когда ядро K( x, y) обращается в нуль при у> х, получается уравнение Вольтерра:
И. у. называется особым, если хотя бы один из пределов интегрирования бесконечен или ядро K( x, y) обращается в бесконечность в одной или нескольких точках квадрата аЈ хЈ b, аЈ yЈ bили на некоторой линии. И. у. может относиться и к функциям нескольких переменных: таково, например, уравнение
Рассматриваются также нелинейные И. у., например уравнения вида
или
Линейные И. у. 2-го рода решаются следующими методами: 1) решение u( x) получается в виде ряда по степеням l (сходящегося в некотором круге |l|< K) с коэффициентами, зависящими от х(метод Вольтерра - Неймана); 2) решение u( x), при тех значениях l, при которых оно вообще существует, выражается через некоторые целые функции от l (метод Фредгольма); 3) в случае, когда ядро симметрично, т. е. К( х, y) є К( у, x), решение u( x) выражается в виде ряда по ортогональным функциям u к( х), являющимся ненулевыми решениями соответствующего однородного уравнения
(последнее имеет отличные от нуля решения лишь при некоторых специальных значениях параметра l = l к , k= 1, 2, ...) (метод Гильберта - Шмидта); 4) в некоторых частных случаях решение сравнительно просто получается с помощью Лапласа преобразования ; 5) в случае, когда
(так называемое вырожденное ядро), отыскание
u(
х) сводится к решению системы алгебраических уравнений. Приближённые решения можно получить, либо применив к
Лит.:Смирнов В. И., Курс высшей математики, 3 изд., т. 4, М., 1957; Петровский И. Г., Лекции по теории интегральных уравнений, 3 изд., М., 1965; Канторович Л. В. и Крылов В. И., Приближённые методы высшего анализа, 5 изд., Л. - М., 1962. Д. А. Васильков. Интегральный логарифм Интегра'льный логари'фм,специальная функция, определяемая интегралом
Этот интеграл не выражается в конечной форме через элементарные функции. Если х> 1, то интеграл понимается в смысле главного значения:
И. л. введён в математический анализ Л. Эйлером в 1768. И. л. li( x) связан с интегральной показательной функцией Ei( x) соотношением li( x) = Ei(ln x). Для больших положительных хфункция li( x) растет как x /ln x.И. л. играет важную роль в аналитической теории чисел, так как число простых чисел, не превосходящих х,приблизительно равно li( x). Лит.:Янке Е., Эмде Ф., Леш Ф., Специальные функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М., 1968. Интегральный синус и интегральный косинус Интегра'льный си'нус и интегра'льный ко'синус- специальные функции, определяемые соответственно интегралами
Эти функции введены итальянским математиком Л. Маскерони в 1790. Однако ещё Л. Эйлеру (1781) было известно, что
Этот интеграл является простейшим примером сходящегося, но не абсолютно сходящегося несобственного интеграла. Функции Si( x) и Ci( x) встречаются в различных вопросах анализа и техники, и для них имеются подробные таблицы. Лит.см. при ст. Интегральный логарифм . Интегратор Интегра'тор,то же, что интегрирующее устройство . Интеграция (биол.) Интегра'ция(биол.), процесс упорядочения, согласования и объединения структур и функций в целостном организме, характерный для живых систем на каждом из уровней их организации. Понятие «И.» ввёл английский учёный Г. Спенсер (1857), связав её с дифференциацией тканей в процессе эволюции и специализацией функций первоначально гомогенной, диффузно реагирующей живой материи. Примеры И. на молекулярном уровне организации: И. аминокислот в сложной молекуле белка, И. нуклеотидов в молекуле нуклеиновой кислоты; на клеточном уровне - оформление клеточного ядра, самовоспроизведение клеток в целом. В многоклеточном организме И. достигает высшего уровня, выражаясь в процессах его онтогенеза; при этом взаимосвязь частей и функций организма возрастает по мере прогрессивной эволюции; система корреляций усложняется, создаются регуляторные механизмы, обеспечивающие устойчивость и целостность развивающегося организма. На уровне сообществ - популяции, видов и биоценозов И. проявляется в сложной и взаимообусловленной эволюции этих биологических систем. Степень И. может служить показателем уровня прогрессивного развития любой живой системы. В физиологии И. - функциональное объединение частных физиологических механизмов в сложно координированную приспособительную деятельность целостного организма. Элементарная единица И. - функциональная система - динамическое объединение центрально-периферических образований, обеспечивающее саморегуляцию определённой функции. Принципы физиологической И. раскрыл (1906) английский физиолог Ч. Шеррингтон на примере координации рефлекторной деятельности спинного мозга (конвергенция, реципрокность, общий конечный путь и т.д.). Эти принципы действуют на всех уровнях нервной системы, включая кору больших полушарий головного мозга. Высшее проявление физиологической И. - условный рефлекс , в котором психические, соматические и вегетативные компоненты сочетаются в осуществлении целостной приспособительной деятельности организма. Лит.:Шмальгаузен И. И., Интеграция биологических систем и их саморегуляция, «Бюлл. Московского общества испытателей природы. Отдел биологический», 1961, т. 66, в. 2, с. 104-34; Анохин П. К., Биология и нейрофизиология условного рефлекса, М., 1968. И. В. Орлов, А. В. Яблоков. Интеграция (восстановление) Интегра'ция(лат. integratio - восстановление, восполнение, от integer - целый), понятие теории систем, означающее состояние связанности отдельных дифференцированных частей в целое, а также процесс, ведущий к такому состоянию. Социальная И. означает наличие упорядоченных отношений между индивидами, группами, организациями, государствами и т. д. При анализе И. различают уровень рассматриваемых систем И. (И. личности, группы, общества и т. д.). При этом термин «интегрированный» имеет различный смысл. Если анализ ведётся на уровне личности (в психологии), под выражением «интегрированная личность» понимается целостный, лишённый внутренних противоречий индивид. То же выражение при анализе на уровне социальной системы относится к личности, интегрированной (включённой) в социальную систему, т. е. к конформной личности. В политической и экономической науках понятие И. может характеризовать внутреннее состояние общества, государства или относиться к государству, интегрированному в более широкую межнациональную общность. И. общества или отдельных государств может осуществляться на основе принуждения, взаимной выгоды или сходства социально-экономического строя, интересов, целей и ценностей различных индивидов, социальных групп, классов, государств. В современных условиях развивается тенденция к межгосударственной И. в экономической и политической областях как в условиях социализма, так и в условиях капитализма. Однако общие объективные предпосылки (научно-техническая революция, тенденция к интернационализации) социалистической и капиталистической И. не означают, что процесс этот в обоих случаях одинаков. Он глубоко различен по социально-экономическим природе, формам, методам, экономическим и политическим последствиям. Термин «И.» применяется также для характеристики процесса сближения и связи наук, происходящего наряду с процессом их дифференциации . Л. Л. Седов. Интеграция социалистическая экономическая Интегра'ция социалисти'ческая экономи'ческая,сознательно и планомерно регулируемый коммунистическими и рабочими партиями и правительствами стран - членов Совета экономической взаимопомощи (СЭВ) процесс международного социалистического разделения труда, сближения их экономик и формирования современной высокоэффективной структуры национальных хозяйств, постепенного сближения и выравнивания уровней их экономического развития, формирования глубоких и устойчивых связей в основных отраслях экономики, науки и техники, расширения и укрепления международного рынка этих стран, совершенствования товарно-денежных отношений. Курс на экономическую интеграцию - общий курс стран - членов СЭВ. Это нашло отражение в документах КПСС, съездов и пленумов коммунистических и рабочих партий других социалистических стран, состоявшихся в 60-е гг. Он зафиксирован как программная установка в решениях 23-й (специальной, апрель 1969) и 24-й (май 1970) сессий СЭВ и в принятой во исполнение этих решений 25-й сессией Совета (июль 1971) Комплексной программе дальнейшего углубления и совершенствования сотрудничества и развития социалистической экономической интеграции стран - членов СЭВ, составленной применительно к конкретным историческим условиям современного этапа строительства социализма и коммунизма. Мероприятия, предусмотренные программой, рассчитаны на поэтапную реализацию в течение 15-20 лет. Экономическая интеграция социалистических стран поставлена в порядок дня всем ходом развития их хозяйства и политики. Она, с одной стороны, является естественным продолжением достигнутых результатов экономического и научно-технического сотрудничества стран социализма, а с другой - свидетельствует о новом историческом этапе их сближения. Новые условия сотрудничества определяются достигнутым социалистическими странами высоким экономическим и научным потенциалом, структурными изменениями в их экономике, возможностями и требованиями научно-технической революции, усилением потребности в интернационализации хозяйственной жизни. В осуществлении И. с. э. находит своё выражение указанная В. И. Лениным тенденция «...к созданию единого, по общему плану регулируемого пролетариатом всех наций, всемирного хозяйства как целого, каковая тенденция вполне явственно обнаружена уже при капитализме и безусловно подлежит дальнейшему развитию и полному завершению при социализме» (Полн. собр. соч., 5 изд., т. 41, с. 164). Закономерный процесс дальнейшего развития И. с. э. - важный фактор роста экономической мощи мировой системы социализма, укрепления её единства, обеспечения в конечном счёте победы социализма над капитализмом. В период после 2-й мировой войны 1939-45 в общемировом развитии особенно резко усилилась объективная тенденция к интернационализации производства и обмена, экономической жизни вообще. Практика развитых в индустриальном отношении стран наглядно показывает, что современные производительные силы могут наиболее эффективно развиваться только как международные производительные силы. Это обусловлено рядом взаимосвязанных факторов. К наиболее существенным из них относятся: интенсификация всего процесса общественного производства, гигантский рост его масштабов, а также ускорение темпов научно-технического прогресса. Международная экономическая интеграция имеет объективную основу в масштабах всего мирового хозяйства, является закономерностью общественного развития. Вместе с тем имеются принципиальные отличия социалистической интеграции от капиталистической, ибо социально-экономическая сущность интеграции, её цели, методы осуществления и последствия обусловливаются природой того общественного строя, в условиях которого она совершается (о капиталистической интеграции см. в ст. Интеграция экономическая). Социалистическая интеграция свободна от противоречий, присущих этому процессу в капиталистическом мире. Её характер и направленность определяются потребностью развития производительных сил и социалистических производств, отношений. Преимущества социалистической интеграции базируются на общности коренных экономических и политических интересов стран, на совпадении их национально-государственных интересов в масштабах социалистического содружества. Развиваясь на основе пролетарского интернационализма, И. с. э. нацелена на всемерный расцвет каждой из братских стран, на укрепление экономического, политического и военного могущества и международного авторитета социалистического содружества. Её осуществление в полной мере отвечает целям и задачам международного коммунистического движения, всех прогрессивных сил современности. Методы государственного руководства интеграционными процессами при социализме основываются на использовании экономических законов социализма. Социалистическая интеграция по своему характеру может быть только планомерно регулируемым процессом. В мероприятиях государств - членов СЭВ по планомерному развитию И. с. э. получает яркое выражение руководящая роль коммунистических и рабочих партий. И. с. э. происходит на основе полной добровольности и не сопровождается созданием наднациональных органов. Социалистические страны вступили в такую полосу развития, когда появляется возможность и необходимость значительно полнее использовать преимущества социалистической организации общественной жизни как в национальном, так и в интернациональном масштабах. В условиях современного этапа строительства социализма и коммунизма, когда центр тяжести экономических задач переместился в сферу глубоких качественных сдвигов, страны СЭВ повысили требования к взаимному сотрудничеству. В этой области главный упор делается на эффективность экономических и научно-технических связей, повышение которой обеспечит экономическая интеграция. Братские страны четко и ясно определили цели социалистической интеграции: более быстрое развитие производительных сил во всех странах СЭВ, достижение наивысшего научно-технического уровня и максимальное повышение экономической эффективности общественного производства. И. с. э. призвана обеспечить совершенствование структуры и рост масштабов производства и содействовать удовлетворению растущих потребностей народного хозяйства стран СЭВ на длительную перспективу в топливе, энергии и сырье, современном оборудовании и товарах народного потребления. И. с. э. направлена на повышение материального и культурного уровня жизни народов социалистических стран, на постепенное сближение и выравнивание уровней экономического развития стран СЭВ, на укрепление их обороноспособности, на обеспечение победы в экономическом соревновании с капитализмом. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60 |
|||||||
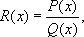

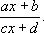

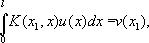
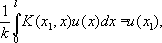
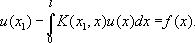



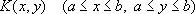

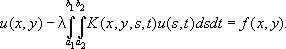


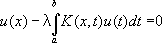
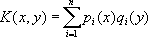
 какую-либо формулу численного интегрирования, либо заменив данное ядро
К(
х,
y) некоторым вырожденным ядром, мало отличающимся от
К(
х,
у). К И. у. часто сводятся краевые задачи для дифференциальных уравнений, обыкновенных и с частными производными; такое сведение имеет и теоретическую и практическую ценность.
какую-либо формулу численного интегрирования, либо заменив данное ядро
К(
х,
y) некоторым вырожденным ядром, мало отличающимся от
К(
х,
у). К И. у. часто сводятся краевые задачи для дифференциальных уравнений, обыкновенных и с частными производными; такое сведение имеет и теоретическую и практическую ценность.