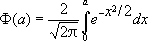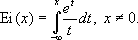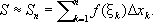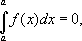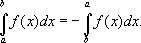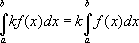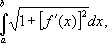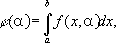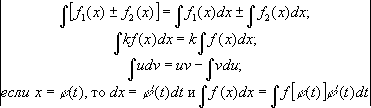|
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ИН)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ИН) - Чтение (стр. 41)
для которого
представляет функцию f( x), порождающую коэффициенты a nи b nпо формулам
где И. понимаются в смысле Лебега. Интеграл Стилтьеса.В конце 19 в. определение интеграла Римана подверглось совершенно иному обобщению, чем то, к которому привело введение понятия меры множества. Это обобщение было дано Т. Стилтьесом (1894). Пусть f( x) - непрерывная функция действительного переменного х, определённая на отрезке [ a, b], и U( x) - определённая на том же отрезке ограниченная монотонная (неубывающая или невозрастающая) функция. Для определения интеграла Стилтьеса берут произвольное разбиение (2) отрезка [ a, b] и составляют сумму f(x 1) [ U( x 1) - U( x 0)] + f(x 2) [ U( x 2) - U( x 1)] +...+ f(x n ) [ U( x n) - U( x n- 1)], (8) где x 1, x 2, ..., x n - произвольные точки, выбранные соответственно на отрезках [ x 0, x 1], [ x 1, x 2], ..., [ x n -1, x n]. Пусть d - наибольшее расстояние между двумя последовательными точками деления в разбиении (2). Если взять любую последовательность разбиений, для которой d стремится к нулю, то сумма (8) будет иметь определённый, всегда один и тот же предел, как бы ни выбирались точки x 1, x 2, ..., x n на соответствующих отрезках. Этот предел называют, следуя Стилтьесу, интегралом функции f( x) относительно функции U( x) и обозначают символом
Интеграл (9) (его называют также интегралом Стилтьеса) существует и в том случае, когда ограниченная функция U( x), не будучи сама монотонной, может быть представлена в виде суммы или разности двух ограниченных монотонных функций U 1( x) и U 2( x): U( x) = U 1( x) - U 2( x), т. е. является функцией с ограниченным изменением (см. Изменение функции ). Если интегрирующая функция U( х) имеет ограниченную и интегрируемую по Риману производную U'( x), то интеграл Стилтьеса сводится к интегралу Римана по формуле
В частности, когда U( x) = х+ С, интеграл Стилтьеса (9) превращается в обыкновенный интеграл Римана (6). Дальнейшие обобщения.Концепции И., созданные Стилтьесом и Лебегом, удалось впоследствии объединить и обобщить на интегрирование по любому (измеримому) множеству в пространстве любого числа измерений. Классические кратные интегралы вполне охватываются этим подходом. Потребности таких дисциплин, как теория вероятностей и общая теория динамическим систем, привели к ещё более широкому понятию абстрактного интеграла Лебега, основанному на общих понятиях меры множества и измеримости функций. Пусть Х -пространство, в котором выделена определённая система Вего подмножеств, называемых «измеримыми», причём эта система обладает свойствами замкнутости по отношению к обычным теоретико-множественным операциям, выполняемым в конечном или счётном числе. Пусть m - конечная мера, заданная на В.Для В-измеримой функции у= f( x), хО Х, принимающей конечное или счётное число значений y 1, y 2, ..., y n, ..., соответственно на попарно непересекающихся множествах A 1, ..., А n, ..., сумма которых есть X, интеграл функции f( x) по мере m, обозначаемый
определяется как сумма ряда
в предположении, что этот ряд абсолютно сходится. Для других fинтегрируемость и И. определяются путём некоторого естественного предельного перехода от указанных кусочно постоянных функций. Пусть А- измеримое множество и j А ( х) = 1 для х, принадлежащих А, и j А ( х) = 0 для х,не принадлежащих А. Тогда интеграл от f( x) по множеству Аопределяют, полагая
При фиксированных m и АИ. в зависимости от fможет рассматриваться как линейный функционал ; при фиксированном fИ., как функция множества А, есть счётно аддитивная функция. Следует отметить, что, несмотря на кажущуюся отвлечённость, это общее понятие И. в наибольшей степени подходит для определения такого понятия, как математическое ожидание (в теории вероятностей), и даже для общей формулировки задачи проверки статистических гипотез. И. по отношению к так называемой мере Винера и различным её аналогам используют в статистической физике (здесь в качестве Хфигурирует пространство непрерывных на каком-либо отрезке функций). Упоминавшиеся до сих пор обобщения понятия И. были такими, что fи | f| оказывались интегрируемыми или неинтегрируемыми одновременно. Обобщения первоначального понятия И. в другом направлении относятся к функциям одного переменного, но зато дают много больше в исследовании интегрирования неограниченных функций. Ещё Коши в случае функции f( x), неограниченной в точке х= с, определил интеграл
когда a< c< b, как предел выражения
при e 1® 0 и e 2® 0 .Аналогично И. с бесконечными пределами
определяется как предел И.
при а® - Ґ и b® + Ґ. Если при этом не требуется интегрируемости | f( x)|, т. е. f( x) интегрируема «не абсолютно», то это определение Коши не поглощается лебеговским. Ещё более широкое обобщение понятия И. в этом направлении было предложено А. Данжуа (1912) и А. Я. Хинчиным (1915). Лит.:Лебег А., Интегрирование и отыскание примитивных функций, пер. с франц., М.-Л., 1934; Сакс С., Теория интеграла, пер. с англ., М., 1949; Камке Э., Интеграл Лебега - Стилтьеса, пер. с нем., М., 1959; Уитни Х., Геометрическая теория интегрирования, пер. с англ., М., 1960; Рудин У., Основы математического анализа, пер. с англ., М., 1966; Данфорд Н., Шварц Дж. Т., Линейные операторы. Общая теория, пер. с англ., М., 1962; Невё Ж., Математические основы теории вероятностей, пер. с франц., М., 1969; Federer Н., Geometric measure theory, В. - Hdlb. - N. Y., 1969. Под редакцией академика А. Н. Колмогорова. Интеграл вероятности Интегра'л вероя'тности,название нескольких связанных друг с другом специальных функций. Интеграл
называют интегралом вероятности Гаусса. Для случайной величины X, имеющей нормальное распределение с математическим ожиданием 0 и дисперсией s 2, вероятность неравенства |X| Ј xравна F( х/s). Наряду с этим название И. в. употребляют для интегралов
Последнюю функцию обозначают обычно erf( x) (от error function - «функция ошибок»). Лит.:Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, М., 1965. Интегральная геометрия Интегра'льная геоме'трия,раздел математики, в котором изучаются некоторые специальные числовые характеристики («меры») для множеств точек, прямых, плоскостей и др. геометрических объектов, вычисляемые, как правило, с помощью интегрирования. При этом «мера» должна удовлетворять требованиям: 1) аддитивности ( мера множества , состоящего из нескольких частей, равна сумме мер этих частей), 2) инвариантности относительно движений (два множества, отличающиеся только положением, имеют одинаковые меры). К И. г. относятся прежде всего задачи нахождения длин, площадей и объёмов, решаемые посредством интегрирования (соответственного простого, двойного и тройного). Толчком для развития И. г. послужили задачи, относящиеся к так называемым геометрическим вероятностям, определяемым как отношение меры множества благоприятных случаев к мере множества всех возможных случаев (по аналогии с классическим определением вероятности, как отношения числа благоприятных случаев к числу всех возможных случаев). Первым и наиболее известным примером является «задача Бюффона» (1777): на плоскость, покрытую рядом параллельных прямых, среди которых каждые две соседние находятся на расстоянии h, падает случайным образом тонкая цилиндрическая игла, длина lкоторой меньше расстояния hмежду параллелями; какова вероятность того, что игла пересечёт одну из этих прямых. Эта задача равносильна следующей: какова вероятность того, что наудачу взятая секущая круга (диаметра h) пересечёт данный отрезок длины l< hс серединой в центре круга. Эту вероятность определяют как отношение «меры» множества прямых, пересекающих данный отрезок, к «мере» множества прямых, пересекающих данный круг. «Меру» множеств прямых, состоящих из секущих выпуклых фигур с контурами конечной длины, вводят так, чтобы выполнялись сформулированные выше два требования: аддитивности и инвариантности. В случае множества всех прямых, пересекающих прямолинейный отрезок, мера этого множества должна быть, в силу инвариантности относительно движений, функцией только длины отрезка. Из требования аддитивности меры следует, что эта функция f( x) должна быть аддитивной: f( x+ y) = f( x) + f( y), а отсюда вытекает f( x) = Cx, где C- постоянная. Итак, на плоскости мера множества всех прямых, пересекающих данный отрезок, должна быть пропорциональна его длине. Коэффициент пропорциональности удобно принять равным 2, т. е. условиться, что за меру множества прямых, пересекающих отрезок длины 1, принимается число 2. Тогда мера множества прямых, пересекающих любой отрезок, окажется равной удвоенной его длине. Рассматривая множество прямых, пересекающих (каждая в двух точках) контур некоторого выпуклого многоугольника, можно вывести, что мера рассматриваемого множества равна просто периметру. Переходя, наконец, к множеству прямых, пересекающих выпуклую замкнутую линию («овал»), нетрудно установить, что на плоскости мерой множества прямых, пересекающих данную выпуклую линию, должна быть длина этой линии. В задаче Бюффона имеют в качестве меры множества благоприятных случаев удвоенную длину (2 l) иглы, а для меры множества возможных случаев - длину (p h) окружности диаметра h; поэтому искомая вероятность р= 2 l/p h. Этот результат не раз проверялся на опытах с бросанием иглы. В одном из таких опытов было произведено 5000 бросаний; при l= 36 мм, h= 45 ммполучилась частота пересечений 0,5064, что даёт приближённое значение для p = 3,1596. С некоторыми видоизменениями изложенная теория может быть перенесена на множества прямых, пересекающих невыпуклые контуры. Вообще, для двухпараметрических множеств прямых на плоскости мера (m) может быть определена формулой m = ттdr dj ,где r, j - полярные координаты проекции полюса на прямую. Если прямая задана уравнением ux+ uy= 1 ( x, y -прямоугольные координаты точки), то
В конце 19 - начале 20 вв. исследования по И. г. ещё связаны с геометрическими вероятностями (работы английского математика М. Крофтона, французского математика А. Пуанкаре), но уже в работе французского математика Э. Картана (1896) они входят в общую теорию интегральных инвариантов, а в 20-х гг. 20 в. складываются в самостоятельную теорию с разнообразными приложениями: к геометрии «в целом», прежде всего к изучению выпуклых областей, к геометрической оптике и теории излучения. Лит.:Бляшке В., Лекции по интегральной геометрии, пер. с нем., «Успехи математических наук», 1938, в. 5; Вlaschke W., Vorlesungen ьber Integralgeometrie, H. 2. B.-Lpz., 1937. Я. С. Дубнов. Интегральная кривая Интегра'льная крива'я,кривая, изображающая геометрически решение дифференциального уравнения или системы дифференциальных уравнений. См. Дифференциальные уравнения. Интегральная показательная функция Интегра'льная показа'тельная фу'нкция,специальная функция, определяемая интегралом
Этот интеграл не выражается в конечной форме через элементарные функции. Если x> 0, то интеграл понимается в смысле главного значения:
Лит. см.при статье Интегральный логарифм. Интегральная схема Интегра'льная схе'ма,интегральная микросхема, микроминиатюрное электронное устройство, все или часть элементов которого нераздельно связаны конструктивно и соединены между собой электрически. Различают 2 основных типа И. с.: полупроводниковые (ПП) и плёночные. ПП И. с. ( рис. 1 ) изготавливают из особо чистых ПП материалов (обычно кремний, германий), в которых перестраивают саму решётку кристаллов так, что отдельные области кристалла становятся элементами сложной схемы. Маленькая пластинка из кристаллического материала размерами ~1 мм 2превращается в сложнейший электронный прибор, эквивалентный радиотехническому блоку из 50-100 и более обычных деталей. Он способен усиливать или генерировать сигналы и выполнять многие другие радиотехнические функции. Технология изготовления ПП И. с. обеспечивает одновременную групповую обработку сразу большого количества схем. Это определяет в значительной степени идентичность схем по характеристикам. ПП И. с. имеют высокую надёжность за счёт использования планарного процесса изготовления и значительного сокращения числа микросоединений элементов в процессе создания схем. ПП И. с. развиваются в направлении всё большей концентрации элементов в одном и том же объёме ПП кристалла, т. е. в направлении повышения степени интеграции И. с. Разработаны И. с., содержащие в одном кристалле сотни и тысячи элементов. В этом случае И. с. превращается в большую интегральную систему (БИС), которую невозможно разрабатывать и изготовлять без использования электронных вычислительных машин высокой производительности. Плёночные И. с. создаются путём осаждения при низком давлении (порядка 1Ч10 -5 мм рт. ст.) различных материалов в виде тонких (толщиною < 1 мкм) или толстых (толщиной > 1 мкм) плёнок на нагретую до определённой температуры полированную подложку (обычно из керамики). В качестве материалов применяют алюминий, золото, титан, нихром, окись тантала, моноокись кремния, титанат бария, окись олова и др. Для получения И. с. с определёнными функциями создаются тонкоплёночные многослойные структуры осаждением на подложку через различные маски (трафареты) материалов с необходимыми свойствами. В таких структурах один из слоев содержит микрорезисторы, другой - микроконденсаторы, несколько следующих - соединительные проводники тока и другие элементы. Все элементы в слоях имеют между собой связи, характерные для конкретных радиотехнических устройств. Плёночные элементы распространены в гибридных И. с. ( рис. 2 ). В этих схемах на подложку сначала наносятся в виде тонких или толстых плёнок пассивные элементы (резисторы, конденсаторы, проводники тока), а затем с помощью микроманипуляторов монтируют активные элементы - бескорпусные ПП микроэлементы (транзисторы и диоды). По своим конструктивным и электрическим характеристикам ПП и гибридные И. с. дополняют друг друга и могут одновременно применяться в одних и тех же радиоэлектронных комплексах. В целях защиты от внешних воздействий И. с. выпускают в защитных корпусах ( рис. 3 ). По количеству элементов различают И. с.: 1-й степени интеграции (до 10 элементов), 2-й степени интеграции (от 10 до 100) и т. д. Размеры отдельных элементов И. с. очень малы (порядка 0,5-10 мкм) и подчас соизмеримы с размерами пылинок (1-100 мкм). Поэтому производство И. с. осуществляется в особо чистых условиях. О технологических процессах изготовления И. с. см. в ст. Микроэлектроника. Создание И. с. развивается по нескольким направлениям: гибридные И. с. с дискретными активными элементами; ПП И. с., выполненные в монолитном блоке ПП материала; совмещенные И. с., в которых активные элементы выполнены в монолитном блоке ПП материала, а пассивные элементы нанесены в виде тонких плёнок; плёночные И. с., в которых активные и пассивные элементы нанесены на подложку в виде тонких плёнок. О применении И. с. см. в ст. Интегральная электроника.
Лит.:Колосов Д. А., Горбунов Ю. И., Наумов Ю. Е., Полупроводниковые твердые схемы, М., 1965; Интегральные схемы. Принципы конструирования и производства, пер, с англ., под ред. А. А. Колосова, М., 1968; Интегральные схемы. Основы проектирования и технологии, пер. с англ., под ред. К. И. Мартюшова, М., 1970. И. Е. Ефимов. 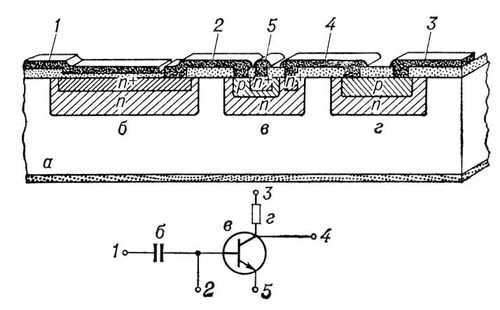
Рис. 1. Поперечное сечение и электрическая схема полупроводниковой интегральной схемы. На рис. сгущенными точками показаны слои проводников тока из алюминия; разреженными точками показаны слои полупроводника из двуокиси кремния; косыми линиями показаны слои кремния с проводимостью n, с повышенной проводимостью n+ и р - типов: участок полупроводника (подложка )с проводимостью р - типа а образует конденсатор б, транзистор в, резистор г; цифрами отмечены участки интегральной схемы, соответственно обозначенные на электрической схеме. 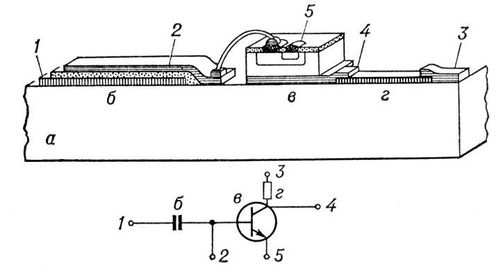
Рис. 2. Поперечное сечение и электрическая схема гибридной интегральной схемы. На рис. разреженными точками показаны слои полупроводника из окиси кремния; вертикальными разреженными линиями показан слой хрома; вертикальными сгущенными линиями показан слой из хромистого никеля (NiCr); горизонтальными линиями показаны слои проводников тока из золота или серебра; на керамической подложке авыполнены конденсатор б, транзистор в, резистор г; цифрами отмечены участки интегральной схемы, соответственно обозначенные на электрической схеме. Интегральная электроника Интегра'льная электро'ника,интегральная микроэлектроника, область электроники, решающая проблемы конструирования, изготовления и применения интегральных схем и функциональных устройств. И. э. представляет собой дальнейший этап развития технологии изготовления полупроводниковых приборов на основе применения высокопроизводительных групповых технологических процессов (см. в ст. Микроэлектроника ). Основные разработки в области И. э. направлены на создание: интегральных схем (полупроводниковых, плёночных, гибридных), функциональных интегральных узлов, молектронных и оптоэлектронных устройств, ионных приборов (см. Молекулярная электроника и Оптоэлектроника ). Наиболее развита полупроводниковая и плёночная (гибридная) микроэлектроника, обеспечивающая массовое промышленное производство стандартных интегральных схем. Особенности развития этих направлений заключаются в непрерывном повышении функциональной сложности и увеличении степени интеграции схем. Оба направления тесно взаимосвязаны и дополняют друг друга. Функциональные интегральные узлы, молектронные и оптоэлектронные устройства являются дальнейшим развитием интегральной технологии на основе методов полупроводниковой и плёночной технологии. Интегральные схемы широко применяют в ЭВМ, контрольно-измерительной аппаратуре, бытовых радиоэлектронных приборах, аппаратуре связи и мн. др. Одним из перспективных направлений И. э. является диэлектрическая электроника.
Лит.:Микроэлектроника, Сб. ст., под ред. ф. В. Лукина, в. 1, М., 1967; Введение в микроэлектронику, пер. с англ., под ред. И. П. Степаненко, М., 1968. К. Я. Прохоров. Интегральное исчисление Интегра'льное исчисле'ние,раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения. И. и. тесно связано с дифференциальным исчислением и составляет вместе с ним одну из основных частей математического анализа (или анализа бесконечно малых). Центральными понятиями И. и. являются понятия определённого интеграла и неопределённого интеграла функций одного действительного переменного. Определённый интеграл.Пусть требуется вычислить площадь S«криволинейной трапеции» - фигуры ABCD(см. рис. ), ограниченной дугой непрерывной линии, уравнение которой у= f( x), отрезком ABоси абсцисс и двумя ординатами ADи BC.Для вычисления площади Sэтой криволинейной трапеции основание AB(отрезок [ a, b]) разбивают на nучастков (необязательно равных) точками а= x 0< x 1< ... < x n-1< < x n = b, обозначая длины этих участков D x 1, D x 2, ..., D x n; на каждом таком участке строят прямоугольники с высотами f(x 1), f(x 2), ..., f(x n ) где x k - некоторая точка из отрезка [ x k - 1, x k] (на рис. заштрихован прямоугольник, построенный на k-м участке разбиения; f (x k) - его высота). Сумма S nплощадей построенных прямоугольников рассматривается в качестве приближения к площади Sкриволинейной трапеции: S» S n = f(x 1) D x 1+ f(x 2) D x 2+ f(x n ) D x n или, применяя для сокращения записи символ суммы S (греческая буква «сигма»):
Указанное выражение для площади криволинейной трапеции тем точнее, чем меньше длины D x kучастков разбиения. Для нахождения точного значения площади Sнадо найти предел сумм S nв предположении, что число точек деления неограниченно увеличивается и наибольшая из длин D x kстремится к нулю. Отвлекаясь от геометрического содержания рассмотренной задачи, приходят к понятию определённого интеграла от функции f( x), непрерывной на отрезке [ а, b], как к пределу интегральных сумм S nпри том же предельном переходе. Этот интеграл обозначается
Символ т (удлинённое S- первая буква слова Summa) называется знаком интеграла, f( x) - подинтегральной функцией, числа аи bназываются нижним и верхним пределами определённого интеграла. Если а= b, то, по определению, полагают
кроме того,
Свойства определённого интеграла:
( k -постоянная). Очевидно также, что
(численное значение определённого интеграла не зависит от выбора обозначения переменной интегрирования). К вычислению определённых интегралов сводятся задачи об измерении площадей, ограниченных кривыми (задачи «нахождения квадратур»), длин дуг кривых («спрямление кривых»), площадей поверхностей тел, объёмов тел («нахождение кубатур»), а также задачи определения координат центров тяжести, моментов инерции, пути тела по известной скорости движения, работы, производимой силой, и многие другие задачи естествознания и техники. Например, длина дуги плоской кривой, заданной уравнением у= f( x) на отрезке [ a, b], выражается интегралом
объём тела, образованного вращением этой дуги вокруг оси Ox,- интегралом
поверхность этого тела - интегралом
Фактическое вычисление определённых интегралов осуществляется различными способами. В отдельных случаях определённый интеграл можно найти, непосредственно вычисляя предел соответствующей интегральной суммы. Однако большей частью такой переход к пределу затруднителен. Некоторые определённые интегралы удаётся вычислять с помощью предварительного отыскания неопределённых интегралов (см. ниже). Как правило же, приходится прибегать к приближённому вычислению определённых интегралов, применяя различные квадратурные формулы (например, трапеций формулу , Симпсона формулу ). Такое приближённое вычисление может быть осуществлено на ЭВМ с абсолютной погрешностью, не превышающей любого заданного малого положительного числа. В случаях, не требующих большой точности, для приближённого вычисления определённых интегралов применяют графические методы (см. Графические вычисления ). Понятие определённого интеграла распространяется на случай неограниченного промежутка интегрирования, а также на некоторые классы неограниченных функций. Такие обобщения называются несобственными интегралами . Выражения вида
где функция f( x, a) непрерывна по xназываются интегралами, зависящими от параметра. Они служат основным средством изучения многих специальных функций (см., например, Гамма-функция ). Неопределённый интеграл.Нахождение неопределённых интегралов, или интегрирование, есть операция, обратная дифференцированию. При дифференцировании данной функции ищется её производная. При интегрировании, наоборот, ищется первообразная (или примитивная) функция - такая функция, производная которой равна данной функции. Таким образом, функция F( x) является первообразной для данной функции f( x), если F'( x) = f( x) или, что то же самое, dF( x) = f( x) dx.Данная функция f( x) может иметь различные первообразные, но все они отличаются друг от друга только постоянными слагаемыми. Поэтому все первообразные для f( x) содержатся в выражении F( x) + С, которое называют неопределённым интегралом от функции f( x) и записывают
Определённый интеграл как функция верхнего предела интегрирования
(«интеграл с переменным верхним пределом»), есть одна из первообразных подинтегральной функции. Это позволяет установить основную формулу И. и. (формулу Ньютона - Лейбница):
выражающую численное значение определённого интеграла в виде разности значений какой-либо первообразной подинтегральной функции при верхнем и нижнем пределах интегрирования. Взаимно обратный характер операций интегрирования и дифференцирования выражается равенствами
Отсюда следует возможность получения из формул и правил дифференцирования соответствующих формул и правил интегрирования (см. табл., где C, m, a, k- постоянные и m¹ -1, а> 0). Таблица основных интегралов и правил интегрирования
¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾
¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60 |
|||||||

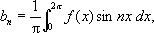


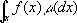 ,
,

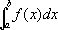 ,
, ,
,
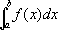 ,
,