 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (ИН)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ИН) - Чтение (стр. 40)
Особенно большое значение учёт И. о. имеет в астрономии, геодезии и др. науках, требующих точнейших измерений. В связи с этим разработка методов исследования И. о. и исключения их влияния на результаты наблюдений и измерений является одной из главных задач теории измерительных инструментов. И. о. могут быть подразделены на 3 категории: 1) ошибки, зависящие от несовершенства изготовления отдельных частей инструмента. Эти ошибки не могут быть ни устранены, ни изменены наблюдателем, но они тщательно исследуются, а вызываемые ими погрешности исключаются или введением соответствующих поправок, или рационально построенной методикой измерений, устраняющей их влияние на окончательные результаты. К этой категории И. о. относятся: ошибки штрихов разделённых кругов, по которым делаются отсчёты направлений на наблюдаемые предметы; ошибки штрихов шкал измерительных приборов; ошибки эксцентриситета, происходящие от несовпадения центра вращения разделённого круга или алидады с центром делений круга; периодические и ходовые ошибки винтов микрометров, связанные с несовершенством их нарезки или монтировки; ошибки от прогиба частей инструмента; ошибки, связанные с оптикой инструмента: дисторсия, астигматизм, кома и др. 2) Ошибки, зависящие от погрешностей сборки и юстировки инструмента, а также от недостаточной точности его установки в положении, требуемом теорией данного способа наблюдений. К этим ошибкам относятся: коллимационная ошибка, заключающаяся в отклонении от 90° угла между визирной линией и осью вращения трубы; ошибки, связанные с наклонением горизонтальной оси инструмента к горизонту и неточностью его установки в нужном азимуте; неточная центрировка линз объектива; некоторые ошибки регистрирующей аппаратуры и др. И. о. этой категории, обнаруживаемые поверками инструмента, могут быть сведены к минимуму перемещением отдельных частей инструмента, предусматриваемым их конструкцией. Остающиеся неустранёнными малые доли этих ошибок определяются с помощью вспомогательных приспособлений (уровень, надир-горизонт, коллиматоры и т. п.) или выводятся из наблюдений (например, ошибка азимута) и влияние их учитывается при обработке наблюдений. 3) Ошибки, связанные с изменением свойств инструмента с течением времени, в частности обусловленные изменением температуры; к этой же категории ошибок относится суммарный эффект всех прочих погрешностей, не учитываемых теорией инструмента. Эти И. о. наиболее сложны. Проявляясь систематически и не обнаруживаясь явно в процессе наблюдений и измерений, они особенно вредны. Выявляются они только при измерениях одних и тех же величин разными инструментами. Так, при сравнении координат звёзд, полученных из наблюдений на разных обсерваториях, или поправок радиосигналов точного времени, определённых различными службами времени, всегда обнаруживаются систематические разности, которые обычно в полтора-два раза, а иногда и в пять-шесть раз превосходят присущие данным методам и инструментам случайные ошибки. Одной из важных задач является нахождение, тщательное исследование и, по возможности, устранение причин, вызывающих И. о. этой категории. См. также Погрешности измерений . Лит.:Блажко С. Н., Курс практической астрономии, 3 изд., М.-Л., 1951; Зверев М. С., Исследование результатов астрономических наблюдений Службы времени ГАИШ за 1941-44 гг., «Труды Государственного астрономического института им. П. К. Штернберга», 1950, т. 18. в. 2; Щеглов В. П., Опыт исследования некоторых систематических ошибок..., «Астрономический журнал», 1950, т. 27, в. 6; Васильев В. М., О разностях температуры отдельных частей трех пассажных инструментов Службы времени, там же, 1952, т. 29, в. 6; Павлов Н. Н., О термических эффектах в перекладывающихся пассажных инструментах, там же, 1953, т. 30, в. 1. Инструментальный институт Инструмента'льный институ'тВсесоюзный научно-исследовательский Министерства станкостроительной и инструментальной промышленности (ВНИИ), основан в Москве в 1943. Разрабатывает научно-технические и теоретические основы процессов резания, конструирования, технологии производства и эксплуатации режущего инструмента, исследует инструментальные материалы и др. Самостоятельные отделы института: стандартизации и нормализации; типажа; патентно-лицензионных работ. Секторы: инструмента общего назначения; инструментальной оснастки автоматических линий, агрегатных и специальных станков; зуборезного инструмента; технологический и т. д. (всего 13 секторов). Имеет заочную аспирантуру. Периодически издаёт «Сборники трудов» (с 1952), а также информационные и руководящие материалы по инструментальному делу. Инструментовка (в литературе) Инструменто'вка,звукопись, упорядоченный подбор звуков в стихе или в прозе, организующий художественное единство отрезков текста: аллитерации, ассонанс, звукоподражание и т. п. См. Фоника . Инструментовка (в музыке) Инструменто'вка,изложение музыкального произведения для какого-либо инструментального состава - от камерного ансамбля до симфонического оркестра. В широком смысле слова говорят и об И. для вокального ансамбля, хора. Чаще всего под И. понимается изложение музыки для оркестра. В том же значении нередко используется и термин оркестровка. Порою, однако, этим терминам придают разное значение, понимая под И. изложение для оркестра сочинения, специально задуманного как оркестровое, а под оркестровкой - изложение для оркестра произведения, написанного для другого состава или для какого-либо одного инструмента (например, для фортепиано). И. основывается на использовании наиболее естественных технических и выразительных возможностей каждого инструмента, на соединении звучания однородных и разнородных инструментов, на противопоставлении контрастных звуковых красок. Эволюция И. тесно связана с развитием всего музыкального искусства, со сменой различных стилей; в И. находят отражение и особенности творческой индивидуальности композитора, его отдельного произведения. Примерно с 17 в. стала входить в практику запись оркестровой музыки в виде партитуры ; до этого инструментальный состав обычно не определялся композитором, и одно и то же сочинение могло исполняться различными исполнительскими силами. Искусство И. развивалось параллельно с обогащением музыкального инструментария, совершенствованием техники сольной игры, расширением состава оркестра. Наряду с собственно оркестровыми жанрами видную роль в развитии И. играла опера. Один из важнейших этапов эволюции И. связан с творчеством композиторов венской классической школы - И. Гайдна, В. А. Моцарта, Л. Бетховена. Особенно быстро искусство И. развивалось в 19-20 вв. В это время поиски новых средств И. интенсивно велись в области оркестровой программной музыки . Особое значение приобретает красочность тембров и их сочетаний; в сочинениях Г. Берлиоза, Р. Вагнера, Ф. Листа, Р. Штрауса, Г. Малера увеличение оркестрового состава нередко совмещается с тонкой дифференциацией оркестровых партий. Большой вклад в области И. внесли русские композиторы-классики - М. И. Глинка, Н. А. Римский-Корсаков, П. И. Чайковский, С. В. Рахманинов, А. Н. Скрябин; их традиции трактовки оркестра творчески развивают советские композиторы. Лит.:Каре А., История оркестровки, пер. с англ., М., 1932; Видор Ш. М., Техника современного оркестра, пер. с франц. и доп. Д. Рогаль-Левицкого, М., 1938; Римский -Корсаков Н. А., Основы оркестровки..., 2 изд., ч. 1-2, М.-Л., 1946; Глинка М. И., Заметки об инструментовке, в кн.: М. И. Глинка. Литературное наследие, т. 1, Л.-М., 1952; Василенко С. Н., Инструментовка для симфонического оркестра, т. 1, М., 1952; Berlioz Н., Grand traitй d’instrumentation et d’orchestration modernes, P., 1843. Инсубры Инсу'бры(лат. Insubres), кельтское племя, осевшее в Северной Италии в долине р. По около середины 6 в. до н. э. (по другим источникам, в 4 в. до н. э.). Покорённые римлянами в 222 (окончательно в 194) до н. э., они были быстро романизованы. Инсула И'нсула(лат. insula, буквально - остров), многоэтажный, обычно кирпичный, жилой дом в Древнем Риме, с комнатами или квартирами, предназначенными для сдачи внаём. Появились не позднее 3 в. до н.э. 3-5-этажные И. (помещения которых обычно компоновались вокруг светового дворика, нередко занимая целый квартал) составляли массовую застройку римских городов. Инсулин Инсули'н(от лат. insula - остров), гормон белковой природы, вырабатываемый b-клетками Лангерганса островков поджелудочной железы. Впервые был выделен канадскими учёными Ф. Бантингом и Ч. Бестом (1921-22). Структурная единица И. - мономер с молекулярной массой около 6000. При определении в различных условиях молекулярная масса И. оказывается равной 12000 или 36000, так как в зависимости от условий опыта в молекулу И. объединяется разное число мономеров. Каждый мономер содержит 51 аминокислоту , которые располагаются в виде двух пептидных цепей - А и В, соединённых посредством двух дисульфидных мостиков (-S-S- ). Наличие этих мостиков необходимо для проявления гормональной активности И.: их разрушение приводит к потере активности. И. различных видов животных отличаются только положением некоторых аминокислот в цепи. Структура мономера И., т. е. последовательность расположения в нём аминокислотных остатков, выяснена английским биохимиком Ф. Сангером (1945-56). Это позволило осуществить химический синтез И. И. снижает содержание сахара в крови, задерживая распад гликогена и синтез глюкозы в печени. В то же время И. повышает проницаемость клеточных мембран для глюкозы, способствуя её переходу в ткани. И. повышает использование глюкозы в реакциях пентозофосфатного цикла и ускоряет синтез гликогена в мышцах. Присутствие И. в организме обусловливает преобладание синтеза белков и жирных кислот над их распадом, способствует переходу углеводов в жирные кислоты и образованию жиров. С недостатком И. в организме связано нарушение обмена веществ - диабет сахарный . При лечении диабета применяют препараты И., получаемые из поджелудочных желез убойного скота и других животных. Активность И. определяют биологически (по способности понижать содержание сахара в крови у кроликов). За единицу действия (ЕД) - интернациональную единицу (ИЕ), или международную единицу (МЕ), - принимают 0,04082 мгчистого кристаллического препарата И. Для инъекций И. вводят подкожно или внутримышечно (при приёме через рот И. разрушается желудочным соком). Свободный И. в организме быстро инактивируется под влиянием фермента инсулиназы. Более продолжительным, чем И., действием (наступающим медленнее) обладают препараты И.: суспензия аморфного цинк-инсулина, раствор протамин-цинк-инсулина, суспензия протамин-инсулина и др. Малые дозы И. (также в виде инъекций) применяют при общем истощении, упадке питания и некоторых других заболеваниях. В психиатрической практике И. вводят для вызывания гипогликемических состояний (см. Гипогликемия ). Г. А. Соловьева. Инсульт Инсу'льт(позднелат. insultus - приступ, от лат. insulto - скачу, впрыгиваю), остро развивающееся нарушение мозгового кровообращения, сопровождающееся повреждением ткани мозга и расстройством его функций. Наиболее частыми причинами И. являются гипертоническая болезнь и атеросклероз или их сочетание; нередко И. развивается при заболевании сердца, ревматизме, иногда при болезнях крови и др. Различают геморрагический И. и ишемический И. Геморрагический И. обусловлен кровоизлиянием в мозг; чаще он возникает при гипертонической болезни. Непосредственным толчком к развитию кровоизлияния в мозг во многих случаях бывает эмоциональное или физическое перенапряжение. Излившаяся кровь отчасти разрушает, а отчасти сдавливает окружающую нервную ткань и вызывает отёк мозга. Кровоизлияние обычно сопровождается тяжёлыми общими явлениями - потерей сознания, расстройством дыхания и сердечной деятельности, рвотой. Лицо больного нередко становится багрово-красным. Наблюдаются судороги различного характера. Развиваются те или иные симптомы очагового поражения мозга - параличи конечностей, расстройства чувствительности, нарушения речи и др. В основе ишемического И. лежит размягчение мозговой ткани - мозговой инфаркт. Мозговой инфаркт развивается при закупорке мозговых сосудов атеросклеротической бляшкой, тромбом (кровяным сгустком) или эмболом (кусочком тромба или атеросклеротической бляшки, принесённым током крови из больного сердца или крупного кровеносного сосуда). Мозговой инфаркт может развиться также при нарушении притока крови к какой-либо области мозга вследствие сужения атеросклеротическим процессом или спазмом приносящего кровь к этой области сосуда. При этом ткань мозга в зоне пораженного сосуда перестаёт получать приносимые с кровью кислород и питательные вещества, гибнет и размягчается. Во многих случаях в происхождении ишемического И. большое значение имеет атеросклеротическое поражение крупных (так называемых магистральных) сосудов головного мозга, сосудов, проходящих на шее (сонные и позвоночные артерии), а также неврогенные и обменные факторы. Развитию ишемического И. способствуют ослабление сердечной деятельности, падение артериального давления, повышение свёртываемости крови. Развитию ишемического И. часто предшествуют преходящие нарушения мозгового кровоснабжения, проявляющиеся кратковременными онемениями в различных частях тела, слабостью конечностей, нарушениями речи, головокружениями или др. расстройствами. Лицо у больного при возникновении ишемического И. бледнеет. Параличи, нарушение чувствительности, речи и др. симптомы нередко нарастают в своей интенсивности постепенно (при геморрагическом И. они возникают обычно внезапно и быстро). Сознание утрачивается лишь в очень тяжёлых случаях. Иногда для правильной диагностики и выбора целесообразного лечения необходимо исследование спинномозговой жидкости, крови и рентгенографическое исследование сосудов мозга с применением контрастных веществ (ангиография). Лечение: полный покой, строгий постельный режим; мероприятия, направленные на устранение сердечно-сосудистых расстройств, предупреждение и устранение нарушений дыхания, на улучшение кровоснабжения мозга и борьбу с отёком мозга, причём выбор методов лечения зависит от типа И. Разрабатываются хирургические методы лечения кровоизлияний в мозг и устранения сужений и закупорки сосудов, ведущих к нарушениям мозгового кровообращения ишемического характера (при поражении магистральных сосудов головного мозга). Для лечения последствий И. используются лечебная гимнастика, массаж, занятия с логопедом и др. Профилактика И.: правильный режим труда, отдыха и питания, устранение нервно-психического перенапряжения, лечение общего сосудистого заболевания. Лит.:Лурье З. Л., Расстройства мозгового кровообращения, 2 изд., М., 1959; Боголепов Н. К., Сосудистые заболевания нервной системы, в кн.: Многотомное руководство по неврологии, т. 4, ч. 1, М., 1963; Шмидт Е, В., Стеноз и тромбоз сонных артерий и нарушения мозгового кровообращения, М., 1963; Нарушения мозгового кровообращения и их хирургическое лечение, М., 1967. Д. К. Лунев. Инсценировка Инсцениро'вка[от лат. In - в, на и scaena (scena) - сцена], 1) переработка для сцены литературного произведения, написанного не в драматургической форме. В отличие от вольного использования эпических мотивов, как то было в античной драме или у У. Шекспира, И. имеет целью не столько создание нового самостоятельного произведения, сколько театральную адаптацию прозы. Первые значительные И. в России принадлежат А. А. Шаховскому (переработки произведений В. Скотта и А. С. Пушкина). Отвергнув тип ремесленной переделки романов в «хорошо скроенные пьесы», характерной для 2-й половины 19 в., В. И. Немирович-Данченко на сцене МХТ искал романную форму спектакля, ставил И.-монтажи. Инсценировочные принципы - объединение контрастных эпизодов, более свободная и ёмкая конструкция, многочастность - повлияли на советскую драму. Многие её первенцы явились авторскими И., в том числе «Виринея» Л. Н. Сейфуллиной (совместно с В. П. Правдухиным, 1925), «Дни Турбиных» М. Булгакова (1926), «Бронепоезд 14-69» В. В. Иванова (1927). В середине 20 в. распространены И. документальной прозы. 2) Одна из форм массового агитационного театра в годы революции: на площадях, сливая зрителей с исполнителями, разыгрывались инсценированные моменты истории и суды над реальными или символическими фигурами («Свержение самодержавия», 1919). Этим И. присущи романтическая символика, условность, сочетание патетики и гротеска. Инта Инта',город в Коми АССР. Расположен на левом берегу р. Большая Инта (бассейн Печоры), в 12 кмот ж.-д. станции Инта, в 50 кмк Ю. от Северного полярного круга. 51 тыс. жителей (1972). Добыча угля (Печорский бассейн), ремонтно-механический завод, деревообрабатывающий комбинат, предприятия стройматериалов, ТЭЦ, птицефабрика. Индустриальный техникум. Народный театр. На правом берегу реки пригородное подсобное хозяйство (молоко, мясо). Посёлок И. образован в 1940, город - с 1954. Лит.:Гулецкий Г. П., Инта, Сыктывкар, 1968. Инталия Инта'лия(от итал. intaglio - резьба), резной камень (гемма) с углублённым изображением. И. служили главным образом печатями. Появились в 4-м тыс. до н. э. (в странах Древнего Востока), широко распространились в период античности. Илл. см. к ст. Глиптика. 
Цилиндрическая печать с изображением мифологических персонажей и животных. Сер. 3-го тыс. до н. э. Шумер. Британский музей. Лондон. 
А. Маснаго. «Язон, поражающий дракона». Камея. 16 в. Италия. Художественно-исторический музей. Вена. 
Печать с изображением Октавиана в образе Нептуна. 1 в. до н. э. Древний Рим. Музей изящных искусств. Бостон. 
П. Е.Доброхотов. «Меркурий, дающий Парису яблоко». 1820. Россия. Эрмитаж. Ленинград. 
Гемма с изображением Горгоны. Сер. 5 в. до н. э. Древняя Греция. Эрмитаж. Ленинград. 
Оттиск цилиндрической печати с изображением мифологических персонажей и животных. Сер. 3-го тыс. до н. э. Шумер. Британский музей. Лондон. 
Дексамен. «Летящая цапля». 3-я четв. 5 в. до н. э. Древняя Греция. Эрмитаж. Ленинград. 
Гемма с изображением бегущего оленя. Ок. 1600 до н. э. Крит. Музей Ашмола. Оксфорд. 
Камея Гонзага с изображением Птолемея II Филадельфа и его жены Арсинби. 3 в. до н. э. Александрия. Эрмитаж. Ленинград. 
Гемма с изображением юноши с петухом. 2-я пол. 5 в. до н. э. Древняя Греция. Эрмитаж. Ленинград. 
Агатоп. Мужской портрет. Между 2 в. до н. э. и 1 в. н. э. Древний Рим. Археологический музей. Флоренция. Интарсия Инта'рсия(от итал. intarsio - инкрустация), вид инкрустации на деревянных предметах (мебели и т. д.): фигурные изображения или узоры из пластинок дерева, разных по текстуре и цвету, врезанных в поверхность деревянного предмета. Наивысшего расцвета И. достигла в Италии в 15 в. Лит.:Krauss F., Intarsien, 3. Aufl., Lpz., 1958. 
Интарсия. Исповедальня. Италия. Ок. 1500. Музей Виктории и Альберта. Лондон. Интеграл Интегра'л(от лат. integer - целый), одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны, отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой - измерять площади, объёмы, длины дуг, работу сил за определённый промежуток времени и т. п. Соответственно с этим различают неопределенные и определённые И., вычисление которых является задачей интегрального исчисления. Неопределённый интеграл.Первообразная функции f( x) одного действительного переменного - функция F( x), производная которой при каждом значении хравна f( x). Прибавляя постоянную к первообразной какой-либо функции, вновь получают первообразную той же функции. Следовательно, имея одну первообразную F( x) функции f( x), получают общее выражение всех первообразных этой функции в виде F( x) + С.Это общее выражение первообразных называют неопределённым интегралом:
функции f( x). Одна из основных теорем интегрального исчисления устанавливает, что каждая непрерывная функция f( x) действительного переменного имеет неопределённый И. Определённый интеграл. Определённый И. функции f( x) с нижним пределом аи верхним пределом bможно определить как разность
где F( x) есть первообразная функции f( x); определение не зависит от того, какая из первообразных выбрана для вычисления определённого И. Если функция f( x) непрерывна, то приведённое определение в случае a < bравносильно следующему определению, данному О. Коши (1823): рассматривают произвольное разбиение отрезка [ a, b] точками
в каждом отрезке [x i- 1, x i] ( i =1, 2,. .., n) берут произвольную точку x i ( x i- 1Ј x i Ј x i) и образуют сумму
Сумма S nзависит от выбора точек x iи x i . Однако в случае непрерывной функции f( x) суммы S n, получающиеся при различном выборе точек x iи x i , стремятся к вполне определённому пределу, если максимальная из разностей x i- x i- 1 стремится к нулю при n® Ґ. Этот предел и является определённым интегралом
По определению,
Определённый И., как указано выше, выражается через любую первообразную F( x). Обратно, первообразная F( x) может быть записана в виде
где а -произвольная постоянная. В соответствии с этим неопределенный И. записывается в виде
О возникновении понятия И., а также о свойствах неопределенных и определённых И. см. Интегральное исчисление.
Обобщение понятия интеграла Интеграл Римана. О. Коши применял своё определение И. только к непрерывным функциям. Назвать, по определению, интегралом
предел сумм S nпри max( x i - x i- 1) ® 0 во всех тех случаях, когда этот предел однозначно определён, предложил Б. Риман (1853). Он же исследовал условия применимости такого определения. Более совершенную форму этим условиям придал А. Лебег (1902), пользуясь введённым им понятием меры множества (см. Меры теория ). Для интегрируемости в смысле Римана функции f( x) на [ a, b] является необходимой и достаточной совокупность двух условий: f( x) ограничена на [ а, b], множество помещающихся на [ a, b] точек разрыва функции f( x) имеет меру, равную нулю. Таким образом, непрерывность в каждой точке отрезка [ а, b] совсем не обязательна для интегрируемости по Риману. Неопределённый И. и первообразную можно теперь определять формулами (5) и (4). Следует только заметить, что при этом первообразная F( x) не обязана иметь подинтегральную функцию f( x) своей производной в каждой точке. Но в каждой точке непрерывности f( x), т. е., в силу результата Лебега, всюду, кроме, может быть, множества меры, равной нулю, будет
Г. Дарбу (1879) дал определение интеграла Римана, которое делает особенно наглядными условиями существования такого И. Вместо сумм (3) Дарбу вводит суммы (называемые суммами Дарбу)
где
M
k- верхняя грань функции
f(
x)
наотрезке [
x
k-
1,
x
k], а
m
k-нижняя грань
f(
x) на том же отрезке. Если
Интеграл Лебега.Введённое Лебегом понятие меры множества позволило дать значительно более широкое определение И. Чтобы определить И. (6), Лебег делит точками ... < y -2< y -1< y 0< y -1< ... < y i<... область возможных значений переменного у= f( x) и обозначает M iмножество тех точек хиз отрезка [ a, b], для которых y i- 1Ј f( x) < y i. Сумма S определяется равенством S= S ih i m( M i), где h i берётся из отрезка y i- 1Ј h i < y i, а m( M i) обозначает меру множества M i.Функция f( x) называется интегрируемой в смысле Лебега на отрезке [ a, b], если ряды, определяющие суммы S, абсолютно сходятся при max( y i-y i- 1) ® 0. Предел этих сумм и называется интегралом Лебега (6). Можно определить первообразную в смысле Лебега как функцию F( x), удовлетворяющую равенству (4), где И. в правой части понимается по Лебегу. Как и в случае интеграла Римана, равенство (7) будет при этом выполняться во всех точках, кроме, может быть, множества, имеющего меру, равную нулю. Для интегрируемости по Лебегу ограниченной функции f( x) необходимо и достаточно, чтобы она принадлежала к числу измеримых функций в смысле Лебега. Все функции, встречающиеся в математическом анализе, измеримы в этом смысле. Более того, до настоящего времени (1972) не построено ни одного индивидуального примера неизмеримой функции. Таким образом, для случая ограниченных функций Лебег решил задачу определения интеграла (6) с общностью, исчерпывающей потребности математического анализа. Среди функций, интегрируемых по Лебегу, имеется сколько угодно функций, всюду разрывных и, следовательно, неинтегрируемых по Риману. Наоборот, каждая интегрируемая по Риману функция интегрируема и по Лебегу. Определение Лебега обобщается на случай интегрирования по полупрямой и по полной прямой, т. е. на случай И. вида
После этого обобщения теория Лебега охватывает все случаи абсолютно сходящихся несобственных интегралов. Общность, достигнутая в определении Лебега, весьма существенна во многих вопросах математического анализа; например, только с введением интеграла Лебега могла быть установлена теорема Фишера - Риса в теории тригонометрических рядов, в силу которой любой ряд
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60 |
|||||||




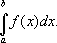





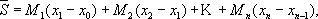

 нижняя грань сумм
нижняя грань сумм
 , а
, а
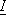 - верхняя грань сумм
- верхняя грань сумм
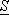 , то для существования интеграла Римана необходимо и достаточно условие
, то для существования интеграла Римана необходимо и достаточно условие
 Общее значение
Общее значение
 величин
величин
 и
и
 и является интегралом Римана (6). Сами величины
и является интегралом Римана (6). Сами величины
 и
и
 называются верхним и, соответственно, нижним интегралами Дарбу.
называются верхним и, соответственно, нижним интегралами Дарбу.
