 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (ХА)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ХА) - Чтение (стр. 14)
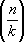 , если (
n,
k) = 1, , если (
n,
k) = 1,
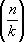 -
Якоби символ
,
k> 1 - нечётное натуральное число. Х. степени
qпо модулю
kназывается Х., равный единице для чисел и, для которых разрешимо сравнение
x
qє
a(mod
k) (см.
Степенной вычет
). Такие Х. играют важную роль в теории алгебраических чисел. Многие вопросы теории чисел (например, вопрос о распределении простых чисел) связаны с изучением функций
L(
sc) = -
Якоби символ
,
k> 1 - нечётное натуральное число. Х. степени
qпо модулю
kназывается Х., равный единице для чисел и, для которых разрешимо сравнение
x
qє
a(mod
k) (см.
Степенной вычет
). Такие Х. играют важную роль в теории алгебраических чисел. Многие вопросы теории чисел (например, вопрос о распределении простых чисел) связаны с изучением функций
L(
sc) =
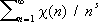 (т. н.
L-функций Дирихле). Частным случаем таких функций является
дзета-функция
x(
s), для которой Х (
n) є 1. (т. н.
L-функций Дирихле). Частным случаем таких функций является
дзета-функция
x(
s), для которой Х (
n) є 1.
Условие периодичности c( n+ k) = c( n) позволяет трактовать характеры c( n, k) при фиксированном k> 1 как функции, заданные на приведённой системе вычетов по модулю k, рассматриваемой как группа по умножению, и удовлетворяющие там функциональному уравнению: c( ab) = c( a) c( b). (1) Такая трактовка понятия Х. позволяет непосредственно перенести его на любую конечную коммутативную группу G. При этом, если n- порядок, e- единица, a- произвольный элемент группы G, то [c( a)] n = c( a n) =c( e) = 1, т. е. c( a) - корень n-й степени из единицы: в частности |c( a)| є 1. (2) Х. произвольной коммутативной группы G(не обязательно конечной) называют всякую функцию c( а), определённую на Gи удовлетворяющую условиям (1) и (2). Если G- топологическая группа, то требуют ещё, чтобы c( а) была непрерывна. Совокупность всех Х. группы Gобразует группу G 1, относительно обыкновенного умножения Х. как функций. Если Gконечна, то G 1изоморфна G. Для бесконечных групп это уже, вообще говоря, неверно. Например, если G- группа целых чисел, то её Х. служат c( n) = e in j, где (j - любое действительное число, приведённое по модулю 2p, так что группа Х. совпадает с группой вращений окружности. В свою очередь, группа Х. для группы вращений окружности совпадает с группой целых чисел [каждый такой Х. имеет вид: c(j) = e in j]. Эта двойственность была обобщена Л. С. Понтрягиным на широкий класс групп и применена к решению важных проблем топологии (т. н. проблем двойственности для компактов). Лит.:Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1973; Чудаков Н. Г., Введение в теорию L-функций Дирихле, М. - Л., 1947; Ленг С., Алгебра, пер. с англ., М., 1968; Боревич З. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972. Характер (в психологии) Хара'ктер(от греч. charakter - отпечаток, признак, отличительная черта) в психологии, целостный и устойчивый индивидуальный склад душевной жизни человека, её тип, «нрав» человека, проявляющийся в отдельных актах и состояниях его психической жизни, а также в его манерах, привычках, складе ума и свойственном человеку круге эмоциональной жизни. Х. человека выступает в качестве основы его поведения и составляет предмет изучения характерологии . Характер (литератур.) Хара'ктерлитературный, образ человека, очерченный с известной полнотой и индивидуальной определённостью, через который раскрываются как обусловленный данной общественно-исторической ситуацией тип поведения (поступки, мысли, переживания, речевая деятельность), так и присущая автору нравственно-эстетическая концепция человеческого существования. Художественный Х. являет собой органическое единство общего, повторяющегося и индивидуального, неповторимого; объективного (социально-психологическая реальность человеческой жизни, послужившая прообразом для литературного Х.) и субъективного (осмысление и оценка прообраза автором). В результате Х. в искусстве предстаёт «новой реальностью», художественно «сотворённой» личностью, которая, отображая реальный человеческий тип, идеологически проясняет его. Именно концептуальность литературного образа человека отличает понятие Х. в литературоведении от значений этого термина в психологии, философии, социологии. Представление о Х. литературного героя создаётся посредством внешних и внутренних «жестов» (в т. ч. речи) персонажа, его внешности, авторскими и иными характеристиками, местом и ролью персонажа в развитии сюжета . Соотношение в пределах произведения Х. и обстоятельств, являющихся художественным воспроизведением социально-исторической, духовно-культурной и природной среды, составляет художественную ситуацию. Противоречия между человеком и обществом, между человеком и природой, его «земной участью», а также внутреннего противоречия человеческих Х. воплощаются в конфликтах художественных. Воспроизведение Х. в его многоплановости и динамике - специфическое свойство художественной литературы в целом (и большинства театральных и кинематографических жанров на словесно-сюжетной основе). Обращение к изображению Х. знаменует выделение литературы как искусства из синкретической, «долитературной» религиозно-публицистической словесности «библейского» или средневекового типа. Само понятие Х. формируется в Древней Греции, где впервые вполне осуществилось выделение литературно-художественного творчества в особую область духовной культуры. Однако у древних понимание Х. как лит. категории отличалось от современного: поскольку в раскрытии идейного содержания главенствовал сюжет (событие), персонажи различались прежде всего не своими Х., а своей ролью в изображаемых событиях. В новое время утверждается иное соотношение Х. и сюжета: не факты, а «... характеры действующих лиц, благодаря которым факты осуществились, заставляют поэта избрать предпочтительнее то, а не другое событие. Только характеры священны для него» (Лессинг Г. Э., Гамбургская драматургия, М. - Л., 1936, с. 92). Понимание самостоятельного идейно-художественного значения Х. персонажа возникает уже в античной литературе; например, в «Параллельных жизнеописаниях» Плутарха герои сравниваются и по типу «судьбы», и по типу Х. Подобная характерологическая двумерность доминирует вплоть до 18 в. (по Д. Дидро - соотношение прирождённого «нрава» и «общественного положения»). В рамках данного многовекового периода особо выделяются две эпохи: литература Возрождения и классицизма. Ренессансный Х. теряет очертания определенного «нрава», растворяясь в естественной родовой стихии человеческой «природы» (герой мог самовольно, как бы актёрствуя, менять типы поведения). При этом соотнесение общечеловеческого в Х. героя с его ситуативной функцией - судьбой - выявляло неадекватность герою его социально-исторической судьбы (предвосхищение характерологического принципа реализма 19-20 вв.: «Человек или больше своей судьбы, или меньше своей человечности», - М. М. Бахтин, «Вопросы литературы», 1970, № 1, с. 119). У Шекспира многие действующие лица предстали и в «третьем измерении» - носителями индивидуального самосознания. Классицизм, возвратившись к жёсткой статичности Х., одновременно сосредоточил внимание на самосознании личности, совершающей выбор между «долгом» и «чувством». Но воспринимаемая на «фоне» долга и безличной страсти личность в литературе классицизма не самоценна, она лишь средство соотнесения двух параллельных рядов всеобщности. На всех этих стадиях духовного и литературного развития Х. понимался как внеисторическая, универсальная и самотождественная данность человеческой природы, как «... абстракт, присущий отдельному индивиду» (Маркс К., см. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 3, с. 3). В романтизме, провозгласившем самоцельность и автономность личности, возвысившем её как над психологической «природой», так и над социальной судьбой, сложилось новое понимание Х. - как тождественного внутреннему миру личности. Наконец, воссоздание индивидуального Х. как исторически неповторимого взаимоотношения личности и среды стало открытием критического реализма 19 в. (романтическую традицию продолжили символисты и экзистенциалисты). В теории новое понимание художественного Х. было выдвинуто Гегелем: Х. - «... цельная человеческая индивидуальность...», в которой раскрываются те или иные «... всеобщие субстанциальные силы действия»; Х. является «подлинным средоточием» изображения, поскольку он объединяет в себе всеобщность и индивидуальность «... в качестве моментов своей целостности». Х. должен обнаруживаться во всём богатстве своих индивидуальных особенностей, а не быть «... игралищем лишь одной страсти...», ибо в таком случае он «... выступает как существующий вне себя...»; он должен быть «... целым самостоятельным миром, полным, живым человеком, а не аллегорической абстракцией какой-нибудь одной черты характера» («Эстетика», т. 1, М., 1968, с. 244-46). Эта теория, опиравшаяся на художественные достижения прошлого, во многом предвосхищала практику последующей реалистической литературы, где присутствует саморазвивающийся Х. - незавершённая и незавершимая, «текучая» индивидуальность, определяемая её непрерывным взаимодействием с исторически конкретными обстоятельствами. Послегегелевская литературная теория, опиравшаяся на реалистическое искусство, настойчиво подчёркивала значение индивидуально-конкретного в Х., но главное - выдвинула и разработала проблему его «концептуальности», установила необходимость «присутствия» авторского идеологического понимания в изображении Х. В реалистической литературе 19-20 вв. Х. действительно воплощают различные, порой противоположные авторские концепции человеческой личности. У О. Бальзака первоосновой индивидуальности выступает понимаемая в духе антропологизма общечеловеческая природа, а её «текучесть» объясняется незавершимостью внешних воздействий среды на первооснову, мерой которых и «измеряется» индивидуальность личности. У Ф. М. Достоевского индивидуальность воспринимается на фоне детерминизма обстоятельств как мера личностного само определения, когда Х. героя остаётся неисчерпаемым средоточием индивидуальных возможностей. Иной смысл «незавершённости» Х. у Л. Н. Толстого: потребность «ясно высказать текучесть человека, то, что он, один и тот же, то злодей, то ангел, то мудрец, то идиот, то силач, то бессильнейшее существо» (Полное собрание соч., т. 53, 1953, с. 187), объясняется стремлением открыть в индивидуальности, отчуждаемой от других людей общественными условиями жизни, общечеловеческое, родовое, «полного человека». У представителей «нового романа» намечается отказ от художественной индивидуальности в пользу безличной психологии (как следствия отчуждения и конформизма ), для воспроизведения которой Х. начинает играть служебную роль «подпорки». Творчество писателей социалистического реализма , наследуя характерологические достижения предшествующих направлений и прежде всего реалистов 19 в., утверждает новое «видение» детерминирующих обстоятельств: социально-историческую и политическую действительность в её революционном развитии, в связи с чем социально-психологическая индивидуальность Х. в их произведениях сгущается в индивидуальность конкретно-историческую. В литературе 60-70-х гг. 20 в. акцентируется нравственная активность личности, её ответственность за свой духовный мир и судьбы других людей. Лит.:Гегель, Эстетика, т. 1, М., 1968, с. 244-53; Социалистический реализм и классическое наследие. (Проблема характера). Сб. ст., М., 1960; Проблема характера в современной советской литературе, М. - Л., 1962; Бочаров С. Г., Характеры и обстоятельства, в кн.: Теория литературы [кн. 1], М., 1962; Бахтин М. М., Проблемы поэтики Достоевского, 3 изд., М., 1972, с. 78-129; его же, Эпос и роман, в его кн.: Вопросы литературы и эстетики, М., 1975; Лихачев Д. С., Человек в литературе древней Руси, [2 изд.], М., 1970; Гинзбург Л., О психологической прозе [Л.], 1971; Аверинцев С. С., Плутарх и античная биография, М., 1973. В. И. Тюпа. Характеристика (в математике) Характери'стика вматематике, 1) целая часть десятичного логарифма . 2) Понятие теории дифференциальных уравнений с частными производными. Х. дифференциального уравнения 1-го порядка
где Р= P( x, y, z), Q = Q( x, y, z), R = R( x, y, z) -заданные функции, называются кривые, определяемые системой обыкновенных дифференциальных уравнений
Интегрируя систему (2), получают семейство характеристик j( x, y, z) = C 1, y( x, y, z) = C 2( C 1, C 2- произвольные постоянные) как совокупность кривых, касающихся в каждой своей точке вектора { P, Q, R}. Всякая интегральная поверхность уравнения (1) представляет собой геометрическое место Х., пересекающих некоторую кривую; уравнение такой поверхности может быть записано в виде F[j( x, y, z), y( x, y, z)] = 0, где F- некоторая функция двух переменных. Обратно, чтобы найти интегральную поверхность, проходящую через заданную кривую (см. Коши задача ), достаточно построить геометрическое место Х., пересекающих эту кривую. Задача Коши имеет одно и только одно решение, если заданная кривая не является Х. Понятие Х. обобщается на случай дифференциального уравнения 1-го порядка с числом независимых переменных, большим двух. Х. дифференциального уравнения 2-го порядка
были введены Г. Монжем (1784, 1795) как линии, вдоль которых удовлетворяется обыкновенное дифференциальное уравнение
Если уравнение (3) принадлежит к гиперболическому типу, то получаются два семейства Х. с уравнениями x( x, y) = C 1и h( х, у) = C 2( C 1, C 2- произвольные постоянные); взяв x и h за новые аргументы, можно привести уравнение (3) к виду
Для уравнения (3) параболического типа эти семейства совпадают; если выбрать аргумент h произвольно, то уравнение (3) приведется к виду
Уравнение (3) эллиптического типа не имеет вещественных Х.; если записать решение уравнения (4) в виде x ± ih = C, то уравнение (3) преобразуется к виду
Значения решения
ивдоль Х. и значения
Если коэффициенты уравнения (3) зависят от
u,
Лит.см. при ст. Уравнения математической физики . Характеристика (в технике) Характери'стикав технике, взаимосвязь между зависимыми и независимыми переменными, определяющими состояние технического объекта (процесса, прибора, устройства, машины, системы), выраженная в виде текста, таблицы, математической формулы, графика и т.п. Например, зависимости тока от электрического напряжения на участке электрической цепи (см. Вольтамперная характеристика ), расхода топлива автомобилем от пройденного им пути и состояния дороги, громкости и качества звучания громкоговорителя от частоты, времени перемагничивания ферритового сердечника от величины намагничивающего поля. Х. по методике определения подразделяют на детерминированные (статические, динамические) и статистические; по виду аналитические зависимости - на линейные и нелинейные; по назначению - на эксплуатационные, настроечные и т.д. Статической Х. называется зависимость между выходной и входной величинами технической системы в установившихся состояниях. Динамические Х. (частотные, импульсные и др.) отражают реакции изучаемой системы на какие-либо типовые возмущающие воздействия: например, частотная Х. отражает зависимость амплитуды и фазы периодического сигнала на выходе системы от амплитуды и фазы входного гармонического сигнала при изменении только его частоты; импульсная Х. - зависимость изменения во времени сигнала на выходе системы от воздействия входного единичного импульса. В наиболее полной форме динамическая Х. содержатся в динамической математической модели объекта, например в виде дифференциальных уравнений. Статистические Х. (оценки) применяют к объектам, поведение которых во времени меняется случайным образом. К статистическим Х. относятся, например, дисперсия, автокорреляционная функция, спектральная плотность и т.п. Линейными называются все Х., которые могут быть с заданной точностью аппроксимированы выражением вида у= ax+ b, где у- выходное воздействие, x- входное воздействие изучаемой системы, аи b- постоянные коэффициенты. Все остальные Х. - нелинейные; среди них выделяют линеаризуемые Х., которые по частям с известной точностью аппроксимируются указанным выше выражением (см. Линеаризация ). А. В. Кочеров. Характеристическая кривая Характеристи'ческая кривая,одна из важнейших характеристик фотографического материала, выражающая зависимость (при оговорённых условиях экспонирования и проявления) между оптической плотностью полученного на материале почернения фотографического и десятичным логарифмом экспозиции (называемым также количеством освещения), вызвавшей это почернение. См. ст. Сенситометрия ( рис. 1 ) и литература при ней. Характеристическая функция Характеристи'ческая фу'нкцияв математике, 1) то же, что собственная функция . 2) Х. ф. множества А(в современной терминологии - индикатор А) - функция f( x), определённая на некотором множестве Е, содержащем множество А, и принимающая значение f( x) = 1, если xпринадлежит множеству А, и значение f( x) = 0, если xне принадлежит ему. 3) В теории вероятностей Х. ф. f X( t) случайной величины Хопределяется как математическое ожидание величины e itX. Это определение для случайных величин, имеющих плотность вероятности p X( x), приводит к формуле
Например, для случайной величины, имеющей нормальное распределение с параметрами аи s, Х. ф. равна
Свойства Х. ф.: каждой случайной величине Хсоответствует определённая Х. ф. f X( t); распределение вероятностей для Х однозначно определяется по f X( t); при сложении независимых случайных величин соответствующие Х. ф. перемножаются; при надлежащем определении понятия «близости» случайным величинам с близкими распределениями соответствуют Х. ф., мало отличающиеся друг от друга, и, обратно, близким Х. ф. соответствуют случайные величины с близкими распределениями. Указанные свойства лежат в основе применений Х. ф., в частности к выводу предельных теорем теории вероятностей. Впервые аппарат, по существу равнозначный Х. ф., был использован П. Лапласом (1812), но вся сила метода Х. ф. была показана А. М. Ляпуновым (1901), получившим с его помощью свою известную теорему. Понятие Х. ф. может быть обобщено на конечные и бесконечные системы случайных величин (т. е. на случайные векторы и случайные процессы). Теория Х. ф. имеет много общего с теорией Фурье интеграла . Лит.:Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969; Прохоров Ю. В., Розанов Ю. А., Теория вероятностей, 2 изд., М., 1973. Характеристические спектры Характеристи'ческие спе'ктры,линейчатые рентгеновские спектры, вызванные электронными переходами на внутренней оболочки (слои) атомов. Длины волн Х. с. лежат в интервале от 10 -2 нмдо 5Ч10 нми, согласно Мозли закону , зависят от атомного номера элемента. Они не обнаруживают периодических закономерностей, присущих оптическим спектрам, что объясняется сходным строением внутренних электронных оболочек всех элементов. Х. с. возникают при возбуждении атомов рентгеновскими фотонами или ускоренными электронами. При этом выбивается один из внутренних электронов, например с К-оболочки атома, и в ней появляется вакансия, которая заполняется при переходе электрона с L-, М-или более высоко лежащей оболочки с испусканием рентгеновского фотона определённой частоты. Совокупность линий, возникающих при переходах электронов с вышележащих оболочек на K-, L-и т.д. оболочки, называется, соответственно, K-, L-и т.д. сериями. Внутри серии линии принято обозначать индексами a, b, g и т.д. Например, линия перехода L® Kобозначается К a(см. рис. 1 в ст. Рентгеновские спектры ). Дискретность, присущая Х. с. испускания, проявляется и в спектрах поглощения рентгеновских лучей (см. рис. ). Х. с. используют для исследований структуры материалов (см. Рентгеновский структурный анализ , Рентгенография материалов , Рентгеновская топография ), а также в спектральном анализе рентгеновском . А. В. Колпаков. 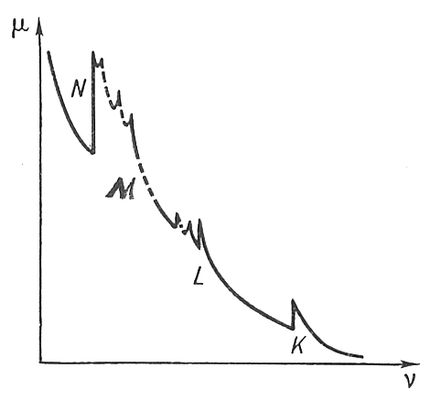
Зависимость коэффициента поглощения m от частоты излучения n для Pt. Показаны К-, L-, M- и N- серии спектра поглощения рентгеновского излучения. Характеристические частоты Характеристи'ческие часто'ты,одинаковые или мало отличающиеся друг от друга частоты колебаний определённых групп атомов в различных молекулах; соответствуют определённым химическим связям (например, С-Н, С-С, С=С, С-Cl и др.). Устойчивость Х. ч. связана с сохранением динамических свойств одинаковых групп атомов в разных молекулах. Во многих случаях можно теоретически рассчитать, обладает ли определённая химическая группа Х. ч. Интенсивности спектральных линий, соответствующих Х. ч. определённой химической группы в различных молекулах, часто имеют близкие значения. Наличие Х. ч. в молекулярных спектрах позволяет делать выводы о строении молекул и имеет большое значение в спектральном анализе . По изменению интенсивностей Х. ч. можно судить о скорости химических процессов. Лит.:Маянц Л. С., Теория и расчет колебаний молекул, М., 1960; Колебания молекул, 2 изд., М., 1972; Свердлов Л. М., Ковнер М. А., Крайнов Е. П., Колебательные спектры многоатомных молекул, М., 1970; Беллами Л. Д., Инфракрасные спектры сложных молекул, пер. с англ., 2 изд., М., 1963; Применение спектроскопии в химии, пер. с англ., М., 1959. Л. Ф. Уткана. Характеристические числа Характеристи'ческие чи'сла(математические), то же, что собственные значения . Характеристический многочлен Характеристи'ческий многочле'н,многочлен, стоящий в левой части характеристического уравнения . Характеристическое уравнение Характеристи'ческое уравне'ниев математике, 1) Х. у. матрицы - алгебраическое уравнение вида
определитель, стоящий в левой части Х. у., получается из определителя матрицы А= || a ik|| n 1вычитанием величины l из диагональных элементов. Этот определитель представляет собой многочлен относительно Х - характеристический многочлен. В раскрытом виде Х. у. записывается так:
где
S
1=
a
11+
a
22+...
a
nn- т. н. след матрицы,
S
2- сумма всех главных миноров 2-го порядка, т. е. миноров вида
Х. у. встречаются в самых разнообразных областях математики, механики, физики, техники. В астрономии при определении вековых возмущений планет также приходят к Х. у.; отсюда и второе название для Х. у. - вековое уравнение. 2) Х. у. линейного дифференциального уравнения с постоянными коэффициентами a 0l y ( n)+ a 1y ( n-1)+... + a n-1y'+ a ny= 0 - алгебраическое уравнение, которое получается из данного дифференциального уравнения после замены функции уи её производных соответствующими степенями величины l, т. е. уравнение a 0l n + a 1l n-1 +... + a n-1 y'+ a ny= 0. К этому уравнению приходят при отыскании частного решения вида у= се l хдля данного дифференциального уравнения. Для системы линейных дифференциальных уравнений
Х. у. записывается при помощи определителя
Х. у. матрицы
A=
Характерный актёр Хара'ктерный актёр,актёр, исполняющий роли, отмеченные ярко выраженным сословным, бытовым внешним и внутренним своеобразием. Отвергнутое как амплуа реалистической школой сценического искусства, понятие Х. а. в современном театре применяется лишь для того, чтобы подчеркнуть доминирующую особенность творческой индивидуальности актёра. Характерный танец Хара'ктерный та'нец,одно из выразительных средств балетного театра, разновидность сценического танца. Первоначально термин «Х. т.» служил определением танца в характере, в образе (в интермедиях, танцах ремесленников, крестьян, разбойников). Позднее балетмейстер К. Блазис стал называть Х. т. все народные танцы, вводившиеся в балетный спектакль. Это значение термина сохраняется и в 20 в. Хореографы и танцовщики классической школы танца строили Х. т. на основе этой школы, используя профессиональную технику. В конце 19 в. был создан экзерсис Х. т. (позднее утвержден как учебная дисциплина хореографических училищ). В современном балетном спектакле Х. т. может быть эпизодом, стать средством раскрытия образа, создания целого спектакля. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 |
|||||||
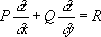 , (1)
, (1)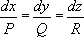 . (2)
. (2)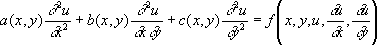 (3)
(3)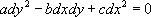 . (4)
. (4)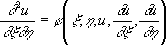 .
.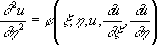 .
.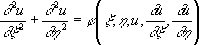 .
.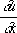 и
и
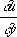 в какой-либо её точке полностью определяют значения этих производных вдоль всей линии [на этом основан т. н. метод Х. решения
краевых задач
для уравнения (3)]; для других линий такой связи нет. С другой стороны, значения
u,
в какой-либо её точке полностью определяют значения этих производных вдоль всей линии [на этом основан т. н. метод Х. решения
краевых задач
для уравнения (3)]; для других линий такой связи нет. С другой стороны, значения
u,
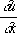 и
и
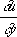 , заданные на линии, не являющейся Х., определяют значения решения вблизи этой линии; для Х. же это не так. Если два решения уравнения (3) совпадают по одну сторону от некоторой линии и различны по другую, то эта линия непременно является Х.
, заданные на линии, не являющейся Х., определяют значения решения вблизи этой линии; для Х. же это не так. Если два решения уравнения (3) совпадают по одну сторону от некоторой линии и различны по другую, то эта линия непременно является Х.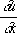 и
и
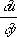 (квазилинейный случай), то Х., определяемые из уравнения (4), будут разные для разных решений. Имеются определения Х. и для уравнений и систем уравнений с частными производными любого порядка.
(квазилинейный случай), то Х., определяемые из уравнения (4), будут разные для разных решений. Имеются определения Х. и для уравнений и систем уравнений с частными производными любого порядка.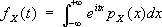 .
.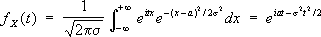 .
.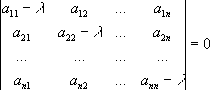 ;
;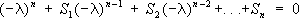 ,
,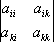 (
i<
k) и т.д., а S
n
- определитель матрицы
А. Корни Х. у. l
1, l
2,..., l
n
называются собственными значениями матрицы
А. У действительной симметричной матрицы, а также у эрмитовой матрицы все l
k
действительны, у действительной кососимметричной матрицы все l
k
чисто мнимые числа; в случае действительной ортогональной матрицы, а также унитарной матрицы все |l
k
| = 1.
(
i<
k) и т.д., а S
n
- определитель матрицы
А. Корни Х. у. l
1, l
2,..., l
n
называются собственными значениями матрицы
А. У действительной симметричной матрицы, а также у эрмитовой матрицы все l
k
действительны, у действительной кососимметричной матрицы все l
k
чисто мнимые числа; в случае действительной ортогональной матрицы, а также унитарной матрицы все |l
k
| = 1.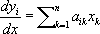 ,
,
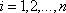 ,
,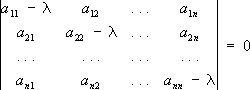
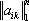 , составленной из коэффициентов уравнений данной системы.
, составленной из коэффициентов уравнений данной системы.