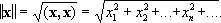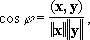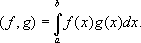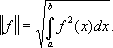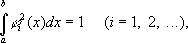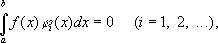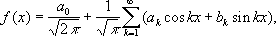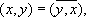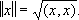Ги'лберта и Э'ллис острова'(Gilbert and Ellice Islands Colony), владение Великобритании в западной части Тихого океана. В состав владения входят: , острова , острова (без островов Кантон и Эндербери — совладение США и Великобритании), часть островов (о-ва Фаннинг, Вашингтон, Рождества) и о. Ошен. Площадь 886 км 2. Население 54 тыс. человек (1969, оценка). Административный центр — г. Тарава (на о. Тарава в группе островов Гилберта). Тропическое земледелие (кокосовая пальма, овощи, фрукты). Рыболовство. Экспорт копры и фосфатов.

       Ги'лберта острова'(Gilbert Islands), группа островов в западной части Тихого океана, в (3°17' с. ш. и 2°38' ю. ш.). Входит в английскую колонию Острова Гилберта и Эллис. Состоит из 16 коралловых атоллов. Площадь 260 км 2. Население 44 тыс. человек (1968). Административный центр — г. Тарава. Климат экваториальный, жаркий и влажный, хотя южные, а отчасти и центральные острова группы подвержены периодическим засухам. Кустарниковая растительность. Выращивание кокосовой пальмы, овощей, фруктов. Г. о. открыты английскими морскими офицерами в период между 1764 и 1824. Названы в честь капитана Дж. Гилберта, посетившего эти острова в 1788.

       Ги'лгит, река па С. -З. Кашмира, правый приток Инда. Длина около 450 км, площадь бассейна 26 тыс. км 2. Берёт начало в хребте Хиндурадж. Питание снеговое и ледниковое. Подъём воды с апреля, наибольший сток — в июле. Зимой водность невелика. Сливаясь с Индом, почти удваивает расход его воды. В районе г. Гилгит образует Гилгитский оазис. Из-за больших скоростей течения и порожистости несудоходна. По долине Г. пролегает древний караванный путь, связывающий С.-В. Афганистана с Индией и Пакистаном.

       Ги'лгуд(Gielgud) Джон Артур (р. 14.4.1904, Лондон), английский актёр и режиссёр. Театральное образование получил в частной школе и Королевской академии драматического искусства. В 1921 дебютировал на сцене театра «Олд Вик» (Лондон). Выступал почти во всех крупных ролях шекспировского репертуара. Большую известность актёру принесло исполнение роли Гамлета в театрах Лондона («Олд Вик», 1929; «Нью», 1934; «Куинс», 1937; «Лицеум», 1939; «Хеймаркет», 1944). Среди др. шекспировских ролей: Ричард II («Ричард II»), король Лир («Король Лир»), Юлий Цезарь («Юлий Цезарь») и др. Ставил пьесы Шекспира: «Ромео и Джульетта» (1935), «Много шума из ничего» (1952), «Двенадцатая ночь» (1955), «Король Лир» (1955), «Гамлет» (1963) и др. Значительной для творчества Г. была работа над ролями в пьесах А. П. Чехова: Трофимов, Гаев («Вишнёвый сад»), Треплев и Тригорин («Чайка»), Вершинин («Три сестры»), Иванов («Иванов»). Г. играл роли в пьесах современных авторов: Себастиан («Обнажённая со скрипкой» Коуарда), Джеймс Каллифер («Сарайчик» Грина), Джулиан («Крошка Алиса» Олби) и др. В 1968 выступил в роли Эдипа («Эдип» Сенеки) в постановке режиссера П. Брука. С 1932 снимается в кино.
        Г. унаследовал и развил лучшие национальные традиции английского сценического искусства, проявив дарование в драме и трагедии. Один из первых среди английских театральных деятелей изучал систему К. С. Станиславского. Г. — большой мастер сценического слова. В классическом репертуаре он сумел передать умонастроение современного молодого поколения, потрясённого противоречиями буржуазного общества. В 1964 гастролировал в Советском Союзе.
        Соч.: Early stages, L., 1939; Stage directions, L., [1965]; в рус. пер. — На сцене и за кулисами. Первые шаги на сцене, Л., 1969.
        Лит.:Agate J., Brief chronicles; a survey of the plays of Shakespeare..., L., 1943; Arthur G., From Phelps to Gielgud..., L., 1936; Gilder R., John Gielgud's Hamlet, L., 1937; Sterne R. L., John Gielgud directs Richard Burton in «Hamlet», L., 1968.
         Ф. М. Крымко.
      Дж. Гилгуд в роли Джона Уортинга («Как важно быть серьёзным» О. Уайльда).

       Ги'лельсЭмиль Григорьевич [р. 6(19).10.1916, Одесса], советский пианист, народный артист СССР (1954). Член КПСС с 1942. Окончил Одесскую консерваторию (1935, класс Б. М. Рейнгбальд) и школу высшего мастерства в Московской консерватории у Г. Г. Нейгауза (1938). Впервые выступил в 1929. С 1936 преподаёт в Московской консерватории (с 1952 профессор). Игра Г., одного из крупнейших пианистов современности, отличается эмоциональностью, мужественностью, огромным виртуозным размахом, ритмической свободой, оригинальностью и свежестью интерпретаций. Концертирует во многих зарубежных странах. Лауреат Международных конкурсов пианистов в Вене (1936.2-я премия) и Брюсселе (им. Изаи, 1938, 1-я премия). Государственная премия СССР (1946), Ленинская премия (1962). Награжден 2 орденами Ленина, 2 др. орденами, а также медалями.
        Лит.:Хентова С., Эмиль Гилельс, 2 изд., М., 1967.
      Э. Г. Гилельс.

       Гиле'я(от греч. hyle — лес), влажнотропический лес Южной Америки, главным образом в бассейне р. Амазонка. Различают 2 основных типа Г.: игапо, или варзеа, — на более низких местах, временами заливаемых рекой, и терра фирма — на более высоких, незаливаемых местах. Последний богаче видами, особенно эндемичными. Для него типичны (преимущественно из семейства бромелиевых, а также аронниковых и др.), выделяющиеся своими формами и яркостью окраски цветков, а также кактусы (особенно виды рипсалис). Эпифиты образуют многочисленные воздушные корни. В Г. Много лиан, встречаются мирмекофильные («сожительствующие» с муравьями) растения из рода цекропиа, трипларис. В Г. произрастают многие ценные виды деревьев, например какао, гевея; здесь добывают копайский бальзам и др. полезные продукты.
        Леса типа Г. распространены также в Центральной Африке (главным образом в бассейне р. Конго) и Юго-Западной Азии. См. также .

       Гилл(Gill) Дейвид (12.6.1843, Абердин, Шотландия, — 24.1.1914, Лондон), шотландский астроном. В 1879—1907 директор обсерватории на мысе Доброй Надежды. В 1880 произвёл определения солнечного параллакса (по своим наблюдениям Марса в великом противостоянии, 1877), дал фотографический обзор части южного неба (1885—89), который лег в основу составления каталога звёзд южного неба нидерландский астрономом Я. К. Каптейном (1896). При помощи проводил измерения звёздных параллаксов, наблюдал прохождение Венеры по диску Солнца (1874), руководил геодезическими работами в Южной Америке.
        Лит.:Селешников С. И., Астрономия и космонавтика, К., 1967; Паннекук А., История астрономии, пер. с англ., М., 1966.

       Ги'лмор(Gilmore) Мэри (16.8.1865, около г. Гоулберн, Новый Южный Уэльс, — 3.12.1962, Сидней), австралийская поэтесса. Увлекшись идеями социалиста-утописта У. Лейна, Г. участвовала в основании коммуны «Новая Австралия» (1893—99) в Парагвае. В течение 23 лет работала в профсоюзной газете «Уоркер» («Worker»). Писала о женской и материнской любви, о радостях и волнениях семейной жизни (сборник «В семье и другие стихи», 1910). В поэзии Г. возникает Австралия, овеянная сказаниями аборигенов, с своеобразным ландшафтом, с горестями трудового народа, с борьбой мужественных людей за социальную справедливость. Сборники: «Страстное сердце» (1918), «Крытая телега» (1925), «Дикий лебедь» (1930), «Под Уилгами» (1932), «За родину Австралию» (1945) и др. Советы профсоюзов Мельбурна, Брисбена и Ньюкасла учредили в 1964 премии им. Гилмор за лучшие литературные произведения.
        Соч. в рус. пер.: [Стихи], «Иностранная литература», 1957, № 8; [Стихи], в сборнике: Поэзия Австралии, М., 1967.
        Лит.:Мэррей-Смит С., Старейшая деятельница австралийской литературы, «Иностранная литература», 1957, № 8; Lawson S., Mary Gilmore, Melb. — [a. o.], 1966.
         Л. М. Касаткина.

       Гилозои'зм(от греч. hyle, здесь — вещество, материя и zoe — жизнь), философское учение об универсальной одушевлённости материи (термин был введён впервые в 17 в.). В истории философии Г. встречается у самых её истоков — в ионийской школе натурфилософов (Фалес, Анаксимандр, Анаксимен); к Г. были близки Гераклит, Эмпедокл, стоики. Элементы Г. содержались в учении Аристотеля. В эпоху Возрождения Г. вновь появляется в учениях итальянских натурфилософов (Б. Телезио, Дж. Бруно), Т. Парацельса и др. Спиноза рассматривал мышление как свойство, присущее всей природе, как атрибут материи. Вслед за ним ряд французских материалистов 18 в. (Дидро, Робине, Дешан) признавал всеобщую одушевлённость материи. Точку зрения, близкую Г., защищал Э. .
        По Г., жизнь и, следовательно, чувствительность присущи всем вещам в природе, всем формам материи. В противоположность этому диалектический материализм рассматривает ощущение как свойство только высокоразвитой органической материи.

       Ги'лрей(Gillray) Джеймс (13.8.1757, Челси, ныне городской район Лондона, — 1.6.1815, Лондон), английский рисовальщик и гравер. Учился в лондонской АХ. Развивая сатирические мотивы творчества У. , Г., наряду с др. английскими графиками конце 18 — начале 19 вв., превратил карикатуру в самостоятельный жанр искусства. Известен главным образом своими политическими карикатурами, исполненными в грубовато-гротескной манере и ярко раскрашенными, в которых осмеивал королевскую семью, аристократию, министров, Наполеона I.
      Произв.: «Новый способ платить национальные долги» (1786), «Король Брабдингнега и Гулливер» (1803—04) — оба офорт.
        Лит.:Некрасова Е., Очерки по истории английской карикатуры конца 18 и начала 19 веков, [Л.], 1935; Hill D., Mr. Gillray the caricaturist, L., 1965.
      Дж. Гилрей. «Очень скользко». Раскрашенный офорт. 1808.

       Ги'лфорд(Guilford) Джой Пол (р. 7.3.1897, шт. Небраска, США), американский психолог. С 1940 профессор психологии Южно-Калифорнийского университета. Один из лидеров психометрического направления в исследованиях мышления и личности. Автор трёхмерной теоретической модели «структуры интеллекта», согласно которой интеллект может быть представлен тремя сторонами: 1) операции, 2) продукты и 3) содержание мышления. Эти различные компоненты мыслительной деятельности выявляются методами (оригинальность, подвижность, гибкость интеллекта и др.; всего до 120 факторов), с помощью которого определяется уровень мыслительных способностей. Опираясь на свою модель и связанные с ней математические методы, Г. выступил инициатором разработки систем психологических тестов для изучения продуктивного мышления и творческих способностей. Чем значительнее индивидуальное решение отклоняется от стандартного, тем выше оно оценивается в качестве показателя творческих способностей личности, С 50-х гг. методы Г. широко используются в США в практических целях для диагностики творческих возможностей инженеров и научных работников. Общий недостаток факторного анализа интеллекта заключается в том, что применяемые при этом способы выявления тех или иных факторов позволяют констатировать лишь сложившиеся системы знаний и действий индивида (а не его мыслительные возможности).
        Соч.: The nature of human intelligence, N. Y., 1967; в рус. пер. — Три стороны интеллекта, в сборнике: Психология мышления, пер. с нем. и англ., М., 1965.
        Лит.:Ярошевский М. Г., Логика развития науки и деятельность учёного, «Вопросы философии», 1969. № 3.
         В. В. Максимов.

       Гильбе'р(Guilbert) Иветт (20.1.1867 Париж, — 2.2.1944 Экс-ан-Прованс) французская эстрадная певица, дебютировала как певица варьете в 1890. Выступала в Париже, гастролировала в Англии, Германии, Австрии, Италии и др. странах, в 1896 в США. Г. создала особый жанр французской лёгкой музыки «песенки конца века» (chansons de fin de siecle), выработала характерный исполнительский стиль (т. н. «амплуа Иветт»), отличавшийся эксцентрически гротесковой манерой. Г. рисовал художник Тулуз-Лотрек (портреты и карикатуры).
        Соч.: Le chanson de ma vie. Mes mйmoires, Р., 1927; Autres temps, autres chants, 12 йd., [Р.], 1946.

       Ги'льберт, Хильберт (Hilbert) Давид (23.1.1862, Велау, близ Кёнигсберга, — 14.2.1943, Гёттинген), немецкий математик. Окончил Кёнигсбергский университет, в 1893—95 профессор там же, в 1895—1930 профессор Гёттингенского университета, до 1933 продолжал читать лекции в университете, после прихода гитлеровцев к власти в Германии (1933) жил в Гёттингене в стороне от университетских дел. Исследования Г оказали большое влияние на развитие многих разделов математики, а его деятельность в Гёттингенском университете в значительной мере содействовала тому, что Гёттинген в 1-й трети 20 в. являлся одним из основных мировых центров математической мысли. Диссертации большого числа крупных математиков (среди них Г. , Р. ) были написаны под руководством Г.
        Научная биография Г. резко распадается на периоды, посвященные работе в какой-либо одной области математики: а) теория инвариантов (1885—93), б) теория алгебраических чисел (1893—98), в) основания геометрии (1898—1902), г) принцип Дирихле и примыкающие к нему проблемы вариационного исчисления и дифференциальных уравнений (1900—06), д) теория интегральных уравнений (1900—10), е) решение проблемы Варинга в теории чисел (1908—09), ж) основы математической физики (1910—22), з) логической основы математики (1922—39).
        В теории инвариантов исследования Г. явились завершением периода бурного развития этой области математики во 2-й половине 19 в. Им доказана основная теорема о существовании конечного базиса системы инвариантов. Работы Г. по теории алгебраических чисел преобразовали эту область математики и стали исходным пунктом её последующего развития. Данное Г. решение проблемы Дирихле положило начало разработке т. н. прямых методов в вариационном исчислении. Построенная Г. теория интегральных уравнений с симметричным ядром составила одну из основ современного функционального анализа (см. ) и особенно спектральной теории линейных операторов. Основания геометрии Г. (1899) стали образцом для дальнейших работ по аксиоматическому построению геометрии. К 1922 у Г. сложило значительно более обширный план обоснования всей математики путём её полной формализации с последующим «метаматематическим» доказательством непротиворечивости формализованной математики. Два тома «Оснований математики», написанных Г. совместно с П. Бернайсом, в которых эта концепция подробно развивается, вышли в 1934 и 1939. Первоначальные надежды Г. в этой области не оправдались: проблема непротиворечивости формализованных математических теорий оказалась глубже и труднее, чем Г. предполагал сначала. Но вся дальнейшая работа над логическими основами математики в большой мере идёт по путям, намеченным Г., и пользуется созданными им концепциями. Считая с логической точки зрения необходимой полную формализацию математики, Г. в то же время верил в силу творческой математической интуиции. Он был большим мастером в высшей степени наглядного изложения математических теорий. В этом отношении замечательна «Наглядная геометрия», написанная Г. совместно с С. Кон-Фоссеном. Для творчества Г. характерны уверенность в неограниченной силе человеческого разума, убеждение в единстве математической науки и единстве математики и естествознания. Собрание сочинений Г., изданное под его наблюдением (1932—35), кончается статьей «Познание природы», а эта статья лозунгом «Мы должны знать — мы будем знать».
        Соч.: Gesammelte Abhandlungen, Bd 1—3, В., 1932—35; в рус. пер. — Основания геометрии, М. — Л., 1948; Основы теоретической логики, М., 1947 (совм. с В. Аккерманом); Наглядная геометрия, 2 изд., М. — Л., 1951 (совм. с С. Кон-Фоссеном).
        Лит.:Проблемы Гильберта. Сборник, под ред. П. С. Александрова, М., 1969; Weyl Н., David Hilbert and his mathematical work, «Bulletin of the American Mathematical Society», 1944, t. 50, p. 612—54; Reid C., Hilbert, В., 1970.
         А. Н. Колмогоров.
      Д. Гильберт.

       Ги'льберт, единица магнитодвижущей силы или разности магнитных потенциалов в Гауссовой и СГСМ абсолютных системах единиц. Названа в честь английского физика У. . Сокращенное обозначение: русское гб, международное Gb. 1 гб= 0,795775 ампер(единицы магнитодвижущей силы ); см. также ( ).

       Ги'льберт, Гилберт (Gilbert) Уильям (24.5.1544, Колчестер, — 30.11.1603, Лондон или Колчестер), английский физик, придворный врач. Г. принадлежит первая теория магнитных явлений. Он впервые выдвинул предположение, что Земля является большим магнитом, и, намагнитив железный шар, показал, что он действует на магнитную стрелку так же, как и Земля. Предположил, что магнитные полюсы Земли совпадают с географическими. Г. установил, что многие тела, подобно янтарю, обладают свойством притягивать лёгкие предметы после натирания. Он исследовал эти свойства и назвал их электрическими (по-гречески янтарь — электрон), впервые введя этот термин в науку. Г. первым в Англии выступил с критикой учения и в защиту учения Н. .
        Соч.: De magneto, magneticisque corporibus et de magno magneto tellure. Physiologia поуа, L., 1600; De mundi nostri sublunaris philosophia nova, Amst., 1651; в рус. пер. — О магните, магнитных телах и большом магните — Земле. Новая физиология, доказанная множеством аргументов и опытов, М., 1956.
        Лит.:Лебедев В. И., Исторические опыты по физике, М. — Л., 1937; Д. Р., Уильям Гильберт. К 50-летию со дня смерти, «Электричество», 1953, № 12.

       Ги'льбертово простра'нство, математическое понятие, обобщающее понятие евклидова пространства на бесконечномерный случай. Возникло на рубеже 19 и 20 вв. в виде естественного логического вывода из работ нем. математика в результате обобщения фактов и методов, относящихся к разложениям функций в ортогональные ряды и к исследованию интегральных уравнений. Постепенно развиваясь, понятие «Г. п.» находило все более широкие приложения в различных разделах математики и теоретической физики; оно принадлежит к числу важнейших понятии математики.
        Первоначально Г. п. понималось как пространство последовательностей со сходящимся рядом квадратов (т. н. пространство l 2). Элементами (векторами) такого пространства являются бесконечные числовые последовательности
         x = (x 1, x 2,..., x n,...)
        такие, что ряд x 2 1+ x 2 2+... + х 2 n+... сходится. Сумму двух векторов х + yи вектор lx, где l— действительное число, определяют естественным образом:
         x + y = (x 1+ y 1,..., x n+ y n,...),
         lx = (lx 1, lx 2, ..., lx n,...)/
        Для любых векторов х, y О l 2формула
         (x, y) = x 1y 1+ x 2y 2+ ... +x ny n+ ...
        определяет их скалярное произведение, а под длиной (нормой) вектора хпонимается неотрицательное число
        

        Скалярное произведение всегда конечно и удовлетворяет неравенству |(х, у)| Ј ||x|| ||y||. Последовательность векторов х nназывается сходящейся к вектору х, если ||х n—х|| ® 0при n ® Ґ. Многие определения и факты теории конечномерных евклидовых пространств переносятся и на Г. п. Например, формула
       
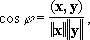        где 0 Ј jЈ pопределяет угол jмежду векторами хи у. Два вектора хи уназываются ортогональными, если ( х, у) = 0. Пространство l 2полно: всякая фундаментальная последовательность Коши элементов этого пространства (т. е. последовательность х n, удовлетворяющая условию ||х п—х m||® 0при n, m ® Ґ) имеет предел. В отличие от евклидовых пространств, Г. п. l 2бесконечномерно, т. е. в нём существуют бесконечные системы линейно независимых векторов; например, такую систему образуют единичные векторы
         e 1= (1, 0, 0,...), e 2= (0, 1, 0,...),...
        При этом для любого вектора xиз l 2имеет место разложение
         x = x 1e 1+ x 2 e 2+...     (1)
        по системе { e n }.
        Другим важным примером Г. п. служит пространство l 2всех измеримых функций, заданных на некотором отрезке [ a, b], для которых конечен интеграл
        

        понимаемый как интеграл в смысле Лебега. При этом функции, отличающиеся друг от друга лишь на множество меры нуль, считаются тождественными. Сложение функций и умножение их на число определяется обычным способом, а под скалярным произведением понимается интеграл
        

        Норма в этом случае равна
        

        Роль единичных векторов предыдущего примера здесь могут играть любые функции j i(x)из L 2, обладающие свойствами ортогональности
        

        и нормированности
        

        а также следующим свойством замкнутости: если f(x)принадлежит L 2и
        

        то f(x)= 0 всюду, кроме множества меры нуль. На отрезке [0,2 p] в качестве такой системы функций можно взять тригонометрическую систему
        

        Разложению (1) соответствует разложение функции f(x)из L 2в ряд Фурье
       
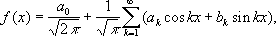        сходящийся к f(x)по норме пространства L 2. При этом для всякой функции f(x)выполняется равенство Парсеваля
        

        Соответствие между функциями f(x)из L 2и последовательностями их коэффициентов Фурье a 0, a 1, b 1, a 2, b 2,... является взаимно однозначным отображением L 2на l 2, сохраняющим операции сложения, умножения на числа, а также сохраняющим длины и скалярные произведения. Т. о., эти пространства изоморфны и изометричны, значит имеют одинаковое строение.
        В более широком смысле под Г. п. понимают произвольное , в котором задано скалярное произведение и которое является полным относительно нормы, порождаемой этим скалярным произведением. В зависимости от того, определено ли для элементов Г. п. Нумножение только на действительные числа или же элементы из Нможно умножать на произвольные комплексные числа, различают действительное и комплексное Г. п. В последнем случае под скалярным произведением понимают комплексную функцию ( х, у), определённую для любой пары х, уэлементов из Ни обладающую следующими свойствами:
        1) ( х, х) = 0 в том и только том случае, если х= 0,
        2) ( х, х) ³ 0 для любого xиз Н,
        3) ( х + у, z) = ( x, z) + ( у, z),
        4) (lx, у) = l(x, у)для любого комплексного числа l,
        5)
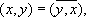        где черта означает комплексно сопряжённую величину. Норма элемента хопределяется равенством
        

        Комплексные Г. п. играют в математике и в её приложениях значительно большую роль, чем действительные Г. п. Одним из важнейших направлений теории Г. п. является изучение линейных операторов в Г. п. (см. ). Именно с этим кругом вопросов связаны многочисленные применения Г. п. в теории дифференциальных и интегральных уравнений, теории вероятностей, квантовой механике и т. д.
        Лит.:Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965; Данфорд Н., Шварц Дж., Линейные операторы, т. 1 — Общая теория, пер. с англ., М., 1962; Дэй М. М., Нормированные линейные пространства, пер. с англ., М., 1961.
         Ю. В. Прохоров.

       Гильви'к, Гийевик (Guillevic) Эжен (р. 5.8.1907, Карнак), французский поэт. Член Французской компартии с 1942. Выступил в печати накануне 2-й мировой войны (стихи в память погибших испанских республиканцев в журнале «Коммюн» — «Соммune», 1939). Деятель Движения Сопротивления, Г. участвовал в подпольной патриотической печати. Трагические картины мира встают в стихах сборника «Из земли и воды» (1942). Лаконичные и суровые строки сборников «Изломы» (1947), «Исполнительный лист» (1947) зовут к борьбе с уродством окружающего. Как глашатай битвы с социальным злом выступает Г. в сборниках «Жажда жизни» и «Вкус мира» (оба 1951), «Земля для счастья» (1952). Темы многих его стихов 50—60-х гг. — вопросы мира и войны, философские раздумья о долге человека («Вместе», 1966; «Эвклидовы мотивы», 1967). Перевёл на французский язык сборник стихов Т. Г. Шевченко, стихи русских поэтов.
        Соч.: Carnac, P., 1961; Sphиre. [Poиmes], P., [1963]; Ville, P., 1969: в рус. пер. — [Стихи], в кн.: Френо. Гильвик. Из французской поэзии, [Предисловие С. Великовского], М., 1969.
        Лит.:Ваксмахер М., Французская литература наших дней, М., 1967, с. 201—211; Daix P., Guillevic, P., 1954; Lacфte R., Guillevic, «Les Lettres franзaises», 1961, 9—15 fйvr., № 862.
         М. Н. Ваксмахер.

       Ги'льгамеш, полулегендарный правитель г. Урука в Шумере (28 в. до н. э.). В 3-м тыс. до н. э. возникли дошедшие до нас шумерские эпические песни о Г. В конце 3-го — начале 2-го тыс. на аккадском (ассиро-вавилонском) языке была составлена большая эпическая поэма о Г. В ней описываются дружба Г. с диким человеком Энкиду, отчаяние Г. после смерти друга и его странствования в поисках тайны бессмертия, посещение им предка Утнапишти, пережившего потоп, и т. д. Легенда о Г. была распространена также у хеттов, хурритов, в Палестине и т. п. Наиболее известен вариант начала 1-го тыс. до н. э. из Ниневии (Куюнджик).
        Публ.: Эпос о Гильгамеше («О всё видавшем»), пер. с аккадского, М. — Л., 1961; Шумерский героический эпос, «Вестник древней истории», 1964, № 3.
         И. М. Дьяконов.

       Ги'льдебранд(Hildebrand) Адольф фон (1847—1921), немецкий скульптор и теоретик искусства; см. А.

       Ги'льдебранд, Хильдебранд (Hildebrand] Бруно (6.3.1812, Наумбург, — 29.1.1878, Иена), немецкий экономист и статистик, один из основателей в политической экономии. Учился в Лейпциге. Профессор в Марбурге, Цюрихе, Берне и Йене. Выдвинул т. н. исторический метод исследования экономического явлений, противопоставлявший научному анализу экономических законов развития общества метод эмпирического сбора статистических и исторических сведений. Предложенная Г. схема развития человечества, заключавшаяся в делении экономического развития общества на три стадии: натуральное, денежное и кредитное хозяйство, исходила из меновой концепции и игнорировала характер собственности на средства производства, определяющей социальную природу экономических формаций и классовую структуру общества. Выступал против марксизма, отрицая сам факт капиталистической эксплуатации. Защищал буржуазную и феодальную частную собственность, оправдывал социальное неравенство, утверждая, что социализм якобы несёт равенство в ущерб свободе.
        Соч.: Nationalцkonomie der Gegenwart und Zukunft, Bd 1, Fr. /М., 1848; рус. пер. — Политическая экономия настоящего и будущего, М., 1960; Naturalwirtschaft, Geldwirtschaft und Kreditwirtschaft, в кн.: Jahrbucher fьr Nationalцkonomie und Statistik, Bd 2, Jena, 1864, S. 1—24.

       Ги'льдебранд(Hildebrand), монашеское имя рим. папы VII.

       Гильде'йские шко'лы, начальные школы, создававшиеся в городах Западной Европы в 13—14 вв. объединениями купцов — . Существовавшие до того времени церковные школы, где главное внимание уделялось преподаванию вероучения и церковному пению, не удовлетворяли нарождавшееся купечество. В Г. ш. преподавание родного языка и арифметики было поставлено значительно лучше, чем в церковных; в некоторых Г. ш. повышенного типа преподавались также грамматика, геометрия и элементы риторики. Г. ш. были платными; в них, как правило, учились дети состоятельных родителей. Католическая церковь отнеслась к Г. ш. враждебно, считая их создание нарушением монополии церкви в школьном деле. С упадком гильдий в 15—16 вв. Г. ш. перешли в ведение городских управлений.

       «Гильде'йский социали'зм», гильдеизм, реформистское течение, возникшее в Великобритании в начале 20 в.