 |
|
Популярные авторы:: Борхес Хорхе Луис :: Толстой Лев Николаевич :: Грин Александр :: Азимов Айзек :: Раззаков Федор :: Горький Максим :: Сименон Жорж :: Чехов Антон Павлович :: Желязны Роджер :: Андреев Леонид Николаевич Популярные книги:: The Boarding House :: Дюна (Книги 1-3) :: Человек, который принял свою жену за шляпу :: Улики :: 100 вещей, которые я сделаю, когда стану злым властелином :: Полет :: Кот, который гулял под землей :: Созвездие Ворона :: Жонглер преступлениями :: Омен. Последняя битва. |
Большая Советская Энциклопедия (ГЕ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ГЕ) - Чтение (стр. 37)
Геогра'фия физи'ческая, см. Физическая география. География экономическая Геогра'фия экономи'ческая, см. Экономическая география . Геодезическая астрономия Геодези'ческая астроно'мия, раздел практической астрономии , наиболее тесно связанный с геодезией и картографией; изучает теорию и методы определения широты jи долготы lместа, а также азимута а направления на земной предмет и местного звёздного времени sиз астрономических наблюдений при геодезических и картографических работах. Т. к. эти наблюдения производятся в полевых условиях, то Г. а. часто называют полевой астрономией. Точка земной поверхности, в которой широта, долгота и азимут определены из астрономических наблюдений, называется астрономическим пунктом . Предмет Г. а. состоит в изучении: а) переносных астрономических инструментов, б) теорий наблюдения небесных светил и методов определения j, l, аи sи в) методов обработки результатов астрономических наблюдений. В Г. а. применяются малые, или переносные, астрономические инструменты, позволяющие измерять зенитные расстояния и направления на небесные светила, а также горизонтальные углы между различными направлениями. Основными инструментами в Г. а. служат: универсальный инструмент , полевой хронометр и радиоприёмник для приёма сигналов времени.
В Г. а. разработан ряд способов астрономических наблюдений, различающихся в зависимости от того, какие величины определяются (время, широта, долгота или азимут), какие светила для этого наблюдаются (звёзды или Солнце) и как и какие величины непосредственно измеряются при наблюдениях небесного светила (зенитное расстояние z, высота h, азимут а*и момент Тпрохождения светила через избранную плоскость). Выбор этих способов зависит от поставленной задачи, точности её решения, наличия инструментов и т. д. При этом небесные координаты наблюдаемого светила, а именно его прямое восхождение аи склонение a, считаются известными; они приводятся в астрономических ежегодниках и каталогах звёзд. Соединив на небесной сфере ( рис. ) полюс P N, зенит места Zи наблюдаемое светило а дугами больших кругов, получим т. н. параллактический треугольник P NZs, в котором угол при вершине Zесть дополнение азимута а*светила до 180° и угол при вершине P Nравен часовому углу tсветила. Все способы астрономических определений основаны на решении параллактического треугольника после измерения его некоторых элементов (см. Сферическая астрономия ). Так, измерив зенитное расстояние Zсветила в момент Тпо хронометру и зная широту jместа, можно определить часовой угол tсветила из выражения cosz = sinj sin d + cosj cosd cost и по равенству t = s - a= Т + u - aнайти поправку uк показанию хронометра и местное звёздное время s. Зная поправку хронометра uи измерив зенитное расстояние Zсветила, можно определить широту jместа. Поправку хронометра выгодно определять из наблюдений звёзд в первом вертикале , а широту места - в меридиане, т. е. в кульминации небесного светила. Если измерить зенитные расстояния двух звёзд, расположенных в меридиане к Ю. или С. от зенита места, то тогда j = d S- z S= d N- z N. Особенно удобны способы, основанные на измерении окулярным микрометром малых разностей зенитных расстояний северных и южных звёзд в меридиане (см. Талькотта способ ). В способах соответственных высот отмечают моменты T 1и T 2прохождений двух звёзд через один и тот же альмукантарат . Если известна j, то получают u(см. Цингера способ ), а если известна u, то определяют j(см. Певцова способ ). Из наблюдений серии равномерно распределённых по азимуту звёзд на постоянной высоте 45° или 30° определяют jи l(см. Мазаева способ ). Азимут а*небесного светила определяют, измеряя его часовой угол или зенитное расстояние и зная широту jместа наблюдения. Прибавляя к азимуту наблюдаемого светила (обычно Полярной звезды) горизонтальный угол Qмежду ним и земным предметом, получают азимут аземного предмета. Разность долгот двух пунктов равна разности местных звёздных времён в этих пунктах или разности поправок хронометра, отнесённых к одному физическому моменту по известному ходу часов , так что l 2- l 1= s 2- s 1= (T + u 2) - (Т + u 1) = u 2- u 1+ T 2- T 1. Долготы lотсчитываются от меридиана Гринвича. Поэтому l = s - S = u - U. Поправки хронометра uотносительно местного звёздного времени sопределяют из наблюдений звёзд, а Uотносительно гринвичского звёздного времени S- из приёма ритмических сигналов времени по радиотелеграфу. В современных высокоточных работах ошибки определения широты, долготы и азимута не превышают ± 0,5". Лит.:Цингер Н. Я., Курс практической астрономии, М., 1924: Вентцель М. К., Полевая астрономия, ч. 1-2, М., 1938-40; Блажко С. Н. . Курс практической астрономии, М. - Л., 1951; Цветков К. А., Практическая астрономия, 2 изд., М., 1951; Кузнецов А. Н., Геодезическая астрономия, М., 1966. А .В. Буткевич. 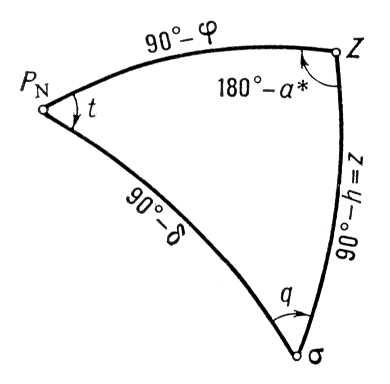
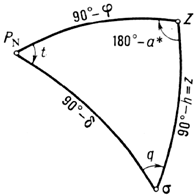
Рис. к ст. Геодезическая астрономия. Геодезическая гравиметрия Геодезическая гравиметрия, раздел геодезии, в котором рассматриваются теории и методы использования результатов измерения силы тяжести для решения научных и практических задач геодезии. Основное содержание Г. г. составляют теории и методы определения внешнего поля потенциала Wсилы тяжести gЗемли по измерениям на земной поверхности Sи астрономо-геодезическим материалам. Г. г. включает также теорию нивелирных высот и обработку астрономо-геодезических сетей в связи с особенностями гравитационного поля Земли. Обычно из этого поля выделяют правильное и известное поле потенциала Uт. н. нормальной Земли сравнения, представляемой в виде уровенного эллипсоида. Центры масс и оси вращения реальной и нормальной Земли совпадают. Основную задачу Г. г. сводят к выводу возмущающего потенциала Т = W - U, который определяют из решения граничных задач математической физики. На земной поверхности Т удовлетворяет граничному условию
где Н- высота над эллипсоидом, g- сила тяжести в поле U, H Q- нормальная высота, выводимая из условия, что приращение ( gdhпотенциала Wот начала счёта высот измерено в поле U, dh- элементарное превышение геометрического нивелирования . Для вывода Т разработано несколько методов, которые сводятся к решению соответствующих интегральных уравнений. В равнинных районах некоторые практические задачи можно решать упрощёнными методами вывода Ти его производных. Эти методы основаны на условии H Q= 0, вводимом после вычисления разностей g - у (HQ). Такой подход, например, допустим при астрономо-гравиметрическом нивелировании . В этом случае задачи Г. г. будут решены в явном виде замкнутыми формулами. Значение Т на земной поверхности определяет формула Стокса (1849)
Современная Г. г. основана на работах (1945-60) М. С. Молоденского и изучает способы решения граничных задач, условия их разрешимости, плотность и точность необходимых измерений. Лит.:Молоденский М. С., Юркина М. И., Еремеев В. Ф., Методы изучения внешнего гравитационного поля и фигуры Земли, «Тр. Центрального научно-исследовательского института геодезии, аэросъёмки и картографии», 1960, в. 131; Бровар В. В., Магницкий В. А., Шимберев Б. П., Теория фигуры Земли, М., 1961. М. И. Юркина. Геодезическая задача Геодези'ческая зада'ча, связана с определением взаимного положения точек земной поверхности и подразделяется на прямую и обратную задачу. Прямой Г. з. называют вычисление геодезических координат - широты и долготы некоторой точки, лежащей на земном эллипсоиде, по координатам др. точки и по длине и азимуту геодезической линии , соединяющей эти точки. Обратная Г. з. заключается в определении по геодезическим координатам двух точек на земном эллипсоиде длины и азимута геодезической линии между этими точками. В зависимости от длины геодезической линии, соединяющей рассматриваемые точки, применяются различные методы и формулы, разработанные в геодезии. По размерам принятого земного эллипсоида составляются таблицы, облегчающие решение Г. з. и рассчитанные на использование определённой системы формул. Г. з. в том и другом виде возникает при обработке триангуляции , а также во всех тех случаях, когда необходимо определить взаимное положение двух точек по длине и направлению соединяющей их линии или же расстояние и направление между этими точками по их геодезическим координатам. В ряде случаев Г. з. решают в пространственных прямоугольных координатах по формулам аналитической геометрии в пространстве. В этих случаях вместо длины и азимута геодезических линии, соединяющей две точки, используют длину и пространственные компоненты направления прямой линии между этими точками. Лит.:Красовский Ф. Н., Руководство по высшей геодезии, ч. 2, М., 1942; Картографические таблицы. Эллипсоид ЦНИИГАиК, «Тр. Центрального научно-исследовательского института геодезии, аэросъёмки и картографии», 1945, в. 41. Геодезическая сеть Геодези'ческая сеть, система точек земной поверхности, взаимное положение которых определено в некоторой единой системе координат и высот над уровнем моря на основании геодезических измерений. Координаты геодезических пунктов Г. с. определяются преимущественно методом триангуляции или полигонометрии . Для определения координат пунктов Г. с. используют также результаты наблюдений искусственных спутников Земли, которые рассматриваются как подвижный носитель координат или как промежуточная точка, служащая для передачи координат на большие расстояния (см. Спутниковая геодезия ). Высоты пунктов Г. с. определяют методами нивелирования . Пункты Г. с. закрепляются на местности геодезическими знаками и являются исходной основой и опорными пунктами при картографировании земной поверхности и геодезических измерениях на местности в связи с различными инженерными изысканиями и хозяйственными мероприятиями. А. А. Изотов. Геодезические знаки Геодези'ческие зна'ки, наземные сооружения и подземные устройства, которым и обозначаются и закрепляются на местности геодезические пункты . Наземная часть Г. з. на пунктах триангуляции и полигонометрии обеспечивает также взаимную видимость между ними и служит штативом для установки измерительного геодезического инструмента и предмета визирования. В зависимости от условий местности и расстояний между пунктами наземная часть Г. з. имеет различную высоту и конструкцию. При взаимной видимости смежных геодезических пунктов с земли наружные Г. з. представляют каменные столбы либо простые деревянные или металлические пирамиды высотой до 6-8 м. Если требуется высота Г. з. от 6-8 мдо 15-18 м, то их строят в виде двойных усечённых пирамид, из которых внутренняя является штативом для инструмента, а внешняя несёт площадку для наблюдателя и визирную цель. При высотах более 15-18 мГ. з. являются сложными сигналами, в которых ноги внутренней пирамиды опираются на столбы внешних пирамид (см. Сигнал геодезический ). Подземная часть Г. з. на пунктах триангуляции и полигонометрии представляет систему бетонных монолитов (или закрепленную в бетонном основании металлическую трубу с вделанной в неё маркой), на которых имеется отверстие или обозначена точка, являющаяся собственно геодезическим пунктом и называемая центром пункта. Пункты нивелирования обозначаются и закрепляются заложенными в грунт Г. з. аналогичного устройства, которые в этом случае называются реперами , или вделанными в стены каменных сооружений чугунными марками. На марках имеется отлитая вместе с ней надпись, указывающая вид и номер геодезического пункта. Лит.:Шишкин В. Н., Руководство по постройке геодезических знаков, 4 изд., М., 1965. А. В. Буткевич. Геодезические и картографические журналы Геодези'ческие и картогра'фические журна'лы, периодические научные издания, освещающие вопросы геодезии, картографии, фотограмметрии, космической геодезии, внешнего гравитационного поля Земли и смежных областей науки. Во всех странах (2-я половина 20 в.) издаётся около 100 Г. и к. ж. Кроме того, в общих журналах, издаваемых академиями наук, научными институтами и университетами также печатаются статьи по геодезии, картографии, фотограмметрии и др. вопросам. Наиболее известными и распространёнными журналами являются: «Геодезия и картография» (с 1956); «Геодезия и аэрофотосъёмка» (из серии «Известия высших учебных заведений», с 1957); «Реферативный журнал. Астрономия и геодезия» (с 1954); «Bulletin gйodйsique» (P., с 1924); «Photogrammetria» (Amst., с 1938); «Photogrammetric Engineering» (Wash., с 1934); «Surveying and Mapping» (Wash., с 1941); «Zeitschrift fьr Vermessungswesen» (Stuttg., с 1872); «Allgemeine Vermessungsnachrichten» (West-Berlin, с 1889); «Vermessungstechnik» (В., с 1953); «Геодезия, картография, землеустройство» (София, с 1961); «Geodйzia йs kartogrбfia» (Bdpst, с 1949); «Przegld geodezyjny» (Warsz., с 1924); «Geodetickэ a kartograficky obzor» (Praha, с 1955). С. Г. Судаков. Специализированные картографические журналы: «Kartographische Nachrichten» (Guhtersloh, с 1951); «Cartography» (Melbourne, с 1954); «Bulletin du Comitй Franзais de Cartographie» (P., с 1958); «Internationales Jahrbuch fьr Kartographie» (Gьtersloh, с 1961); «Map» (Tokyo, с 1963); «The Cartographie Journal» (L., с 1964); «Bollettino dell' Associazione Italiana di Cartografia» (Firenze, с 1964); «The Canadian Cartographer» (Toronto, с 1964); «Polski Przegld Kartograficzny» (Warsz., с 1969). Среди справочно-библиографич. журналов наиболее важны: реферативный журнал «География», выпуск «Картография» (с 1962); «Bibliotheca Cartographica» (Bad Godesberg, с 1957). К. А. Салищев. Геодезические инструменты Геодези'ческие инструме'нты, геодезические приборы, механические, оптико-механические, электрооптические и радиоэлектронные устройства для измерения длин линий, углов, превышений при построении астрономо-геодезической сети и нивелирной сети , съёмке планов, строительстве, монтаже и в процессе эксплуатации больших инженерных сооружений, антенных устройств радиотелескопов и т.п. К Г. и. относятся также инструменты для астрономических определений при геодезических работах и маркшейдерские инструменты. Инструменты и приборы для измерения длин линии. Для обычных измерений длин линий применяют стальные мерные ленты ( рис. 1 ) длиной в 20 или 50 м, которые укладывают по земле, отмечая их концы шпильками. Относительная ошибка измерения лентой зависит от условий местности и в среднем составляет 1:2000. Для более точных измерений применяют ленты из инвара , которые натягивают динамометрами. Таким путём можно снизить ошибку до 1:20000 - 1:50000. Для ещё более точных измерений, главным образом базисов в триангуляции , применяют базисные приборы с подвесными инварными мерными проволоками длиной в 24 м; относительная ошибка таких измерений имеет порядок 1:1000000, т. e. 1 ммна 1 кмдлины измеряемой линии. В геодезических работах применяют также дальномеры , совмещенные со зрительной трубой или являющиеся насадками на зрительную трубу Г. и. Они позволяют искомую длину линии определять из решения треугольника, вершина которого совпадает с передним главным фокусом объектива зрительной трубы инструмента, а его высотой служит измеряемая линия, причём основание и противолежащий ему угол в этом треугольнике известны. Существуют также электрооптические дальномеры и радиодальномеры , позволяющие измерять расстояние по времени прохождения вдоль измеряемой линии световых волн или радиоволн, скорость распространения которых известна. Инструменты для определения направлений и измерения углов. Для простейшего определения направлений линий относительно меридиана служит буссоль , являющаяся или самостоятельным геодезическим инструментом, или принадлежностью других Г. и. Погрешность буссоли составляет 10-15'. Для более точного измерения направлений и углов в геодезии применяются разнообразные инструменты. Прообразом их явилась астролябия , изобретённая ещё до н. э. и состоявшая из круга с делениями, по которому углы отсчитывали с помощью вращающейся линейки с диоптрами , служившими для наведения на предмет. Во 2-й половине 16 в. начали появляться др. угломерные инструменты. например пантометр (астролябия с вертикальным кругом, допускавшая измерение и горизонтальных и вертикальных углов). С 17 в. в угломерных инструментах стали применяться зрительные трубы (1608), микроскопы (1609), верньеры (1631), уровни (1660), сетки нитей (1670). Так сложился основной угломерный инструмент, получивший название теодолита . На рис. 2 представлен большой теодолит Дж. Рамедсна (1783). Теодолит устанавливают на штативе или столике геодезического знака , подъёмными винтами и по уровню приводят вертикальную ось в отвесное положение, поворотами трубы около вертикальной и горизонтальной осей наводят её на визируемую точку и производят отсчёты по кругам. Это даёт направление, а угол получают как разность двух смежных направлений. В современных теодолитах круги изготовляют из оптического стекла, диаметр делений 6-18 см, наиболее употребительный интервал между делениями 20' или 10', отсчётными устройствами служат шкаловые микроскопы с точностью отсчитывания 1'-6» или т. н. оптические микрометры с точностью отсчитывания до 0,2-0,3». В 60-х гг. 20 в. для определения направления истинного (географического) меридиана стали применять т. н. гиротеодолиты и различные гироскопические насадки на теодолиты. Погрешность определения направлений гиротеодолитом составляет 5-10». К осевым, закрепительным и наводящим устройствам угломерных инструментов предъявляют высокие требования. Например, в высокоточных теодолитах угловые колебания вертикальных осей не превышают 2'', в пассажных инструментах допустимая неправильность формы их цапф, на которых вращается зрительная труба, составляет доли микрона. Закрепительные устройства не должны вызывать упругих деформаций в осевых системах и смещений закрепляемых частей инструмента в момент закрепления. Наводящие устройства должны осуществлять весьма тонкие перемещения частей инструмента, например повороты с точностью до долей секунды. Зрительные трубы угломерных и др. Г. и. имеют увеличения в 15-65 раз. Наиболее распространены т. н. трубы с внутренней фокусировкой, снабженной телеобъективом, заднюю компоненту которого, называемую фокусирующей линзой, можно передвигать для получения отчётливого изображения различно удалённых предметов. Точность визирования трубой зависит как от её увеличения, диаметра отверстия объектива, качества даваемого ею изображения, так и от формы, размеров, освещённости и контрастности визируемой цели. С увеличением дальности до цели большее значение приобретает влияние атмосферных помех, снижающих контраст и вызывающих колебания изображения цели. В идеальных условиях хорошие трубы с увеличением в 30-40 раз дают ошибку визирования около 0,3». К теодолитам примыкают т. н. тахеометры-автоматы и тахеометры-полуавтоматы, позволяющие без вычислений, прямо из отсчётов по рейке, получать редуцированные на горизонтальную плоскость расстояния и превышения точек установки рейки или без вычислений определять только расстояния, а превышения вычислять по найденному расстоянию и измеренному углу наклона. Инструменты для измерения превышений. Для нивелирования употребляют главным образом оптико-механические нивелиры с горизонтальным лучом визирования: ими производят отсчёт по рейкам , устанавливаемым на точках, разность высот которых надо определить. Известны также нивелиры с наклонным лучом визирования, позволяющие с одной установки определять значительные превышения, но из-за меньшей точности они не получили широкого распространения. В некоторых случаях, например для привязки островов к материку, употребляют т. н. гидростатические нивелиры, основанные на свойстве сообщающихся сосудов сохранять на одной высоте уровень наполняющей их жидкости. Первые упоминания о нивелирах связаны с именами Герона Александрийского и римского архитектора Марка Витрувия (1 в. до н. э.). Современные очертания нивелиры начали приобретать с появлением уровней и зрительных труб (17 в.). Нивелиры с горизонтальным лучом визирования отличаются схемой соединения между собой трёх основных частей нивелира: зрительной трубы с сеткой нитей, фиксирующей визирный луч, уровня, служащего для приведения этого луча в горизонтальное положение, и подставки, несущей трубу и соединённой с вертикальной осью вращения. С середины 20 в. применяются преимущественно нивелиры с наглухо соединёнными между собой трубой, уровнем и подставкой, получившие название глухих нивелиров. С 50-х гг. 20 в. широкое распространение получили нивелиры с самоустанавливающейся линией визирования, в которых для горизонтирования визирной оси взамен уровня применяют компенсатор, представляющий собой оптическую деталь зрительной трубы, подвешенную на маятниковом подвесе. Впервые в мире такой нивелир был изготовлен в СССР в 1946. При нивелировании употребляют рейки длиной от 1,5 до 4 м. Шкалы реек для точного нивелирования, где расстояние визирования не превосходит 50 м, имеют штрихи шириной в 1 мм, нанесённые через 5 ммна инварной ленте, натянутой в деревянном корпусе пружинами, обеспечивающими постоянство длины шкалы при колебаниях температуры. Для нивелирования низших классов, когда расстояние визирования может достигать 100 м, употребляют деревянные рейки со шкалами из шашек шириной в 1 смс таким же просветом между ними ( рис. 3 ). Инструменты для графических съёмок. Несмотря на широкое развитие методов стереофотограмметрической съёмки планов и карт, ещё находит применение графическая или мензульная съёмка . Основными инструментами для неё являются мензула и кипрегель. Ещё в 19 в. выпускались широко применявшиеся в России кипрегели так называемого типа Главного штаба. В 30-х гг. в СССР изготовлялся оригинальный и портативный для этого времени кипрегель КШВ (Ширяева - Вилема) в комплекте с упрощённой мензулой ( рис. 5 ). История геодезического инструментостроения в России ведёт своё начало со времён Петра I. Изготовлением Г. и. занимались крупнейшие русские учёные и изобретатели, начиная с М. В. Ломоносова и И. П. Кулибина. В дальнейшем (конец 18 - начало 19 вв.) Г. и. изготовлялись в мастерских Академии наук, Главного штаба, Пулковской обсерватории и др., причём большое значение имели труды В. К. Деллепа, В. Я. Струве, А. С. Васильева и др. Однако промышленного изготовления Г. и. в России почти не существовало и потребность в них удовлетворялась преимущественно за счёт импорта. Советское геодезическое инструментоведение началось в 20-х гг. созданием в Москве фабрик «Геодезия» и «Геофизика», где было налажено и конструирование, и серийное производство Г. и. технической точности. В конце 20-х гг. работы по выпуску отечественных высокоточных Г. и. для создания государственных опорных сетей возглавил Ф. Н, Красовский; Г. и. изготовлялись на заводе «Аэрогеоприбор» (ныне экспериментальный Оптико-механический завод в Москве). Оптико-механическая промышленность СССР выпускает ежегодно десятки тысяч Г. и., конструкция и технология производства которых находятся на уровне лучших образцов мировой техники. Лит.:Красовский Ф. Н. и Данилов В. В. Руководство по высшей геодезии, 2 изд., ч. 1. в. 1-2. М., 1938-39; Чеботарёв А. С. Геодезия 2 изд. ч. 1-2 М., 1955-62; Литвинов Б. А., Геодезическое инструментоведение, М., 1956; Елисеев С. В., Геодезические инструменты и приборы, [2 изд.], М., 1959; Араев И. П., Оптические теодолиты средней точности и оптические дальномеры, М., 1965; Гусев Н. А., Маркшейдерско-геодезические инструменты и приборы, 2 изд., М., 1968; Захаров А. И., Новые теодолиты и оптические дальномеры, М., 1970. Г. Г. Гордон. 
Рис. 2. Теодолит Рамсдена. 
Рис. 4. Глухой высокоточный нивелир H1. 
Рис. 1. Мерная лента. 
Рис. 6. Кипрегель КШВ (Ширяева - Вилема). 
Рис. 5. Рейка Высоцкого. Геодезические координаты Геодези'ческие координа'ты, географическая широта и долгота точки земной поверхности, определенные путем геодезических измерений расстояния (главным образом методом триангуляции ) и направления (азимута) от некоторой другой точки, для которой географические координаты известны. Г. к. вычисляются на поверхности референц-эллипсоида,характеризующего фигуру и размеры Земли, и отличаются от широт и долгот, измеренных астрономическими методами, на малые величины, зависящие от неточности элементов принятого эллипсоида и от отклонений отвеса.В состав Г. к. точки входит также ее высота, которая отсчитывается от поверхности принятого референц-эллипсоида и отличается от ее высоты над уровнем моря на величину отклонения геоида от этого эллипсоида. Геодезические линии Геодези'ческие ли'нии, линии на поверхности, достаточно малые дуги которых являются на этой поверхности кратчайшими путями между их концами. На плоскости Г. л. - прямые, на круговом цилиндре - винтовые линии, на сфере- большие круги. Не всякая дуга Г. л. является на поверхности кратчайшим путём; например, на сфере дуга большого круга, бо'льшая полуокружности, не будет на этой сфере кратчайшей между своими концами. Г. л. обладает тем свойством, что их главные нормали являются нормалями к поверхности. Г. л. впервые появились в работах И. Бернулли и Л. Эйлера.Т. к. определение Г. л. связано только с измерениями на поверхности, они относятся к объектам т. н. внутренней геометрии поверхности. Понятие Г. л. переносится в геометрию римановых пространств. Советские математики А. Д. Александров и А. В. Погорелов исследовали аналоги Г. л. на общих выпуклых поверхностях. Понятие Г. л. широко применяется в теоретических и практических вопросах геодезии. Точки земной поверхности проектируются на поверхность земного эллипсоида и соединяются Г. л. При этом применяются некоторые специальные приёмы для перехода от расстояний и углов на земной поверхности к соответствующим дугам Г. л. и углам между ними на поверхности земного эллипсоида. Лит.:Люстерник Л. А., Геодезические линии, 2 изд., М. - Л., 1940; Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М. - Л., 1948; Погорелов А. В., Лекции по дифференциальной геометрии, 4 изд., Хар., 1967; Келль Н. Г., Высшая геодезия и геодезические работы, ч. 1, Л., 1932; Красовский Ф. Н. Руководство по высшей геодезии, ч. 2. М., 1942. Э. Г. Поздняк. Геодезические проекции Геодези'ческие прое'кции, отображения поверхности земного эллипсоида на плоскость, осуществленные по определённым законам. Г. п. применяются для численной обработки геодезических сетей и для решения различных практических задач с использованием результатов геодезических измерений на местности, а также при построении топографических карт масштабов крупнее 1:1000000. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85 |
|||||||
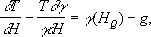
 R- радиус земной сферы,
ds- её элемент и
y- дуга большого круга между фиксированной точкой и текущей точкой, в которой задана сила тяжести. Эта формула описывает внешнее гравитационное поле земной сферы. Из неё можно вывести выражение для любого элемента гравитационного поля Земли в равнинных её областях.
R- радиус земной сферы,
ds- её элемент и
y- дуга большого круга между фиксированной точкой и текущей точкой, в которой задана сила тяжести. Эта формула описывает внешнее гравитационное поле земной сферы. Из неё можно вывести выражение для любого элемента гравитационного поля Земли в равнинных её областях.