Фу'нкия(Funkia), род растений семейства лилейных. Название часто употребляется в цветоводстве вместо правильного —
.
Функции ладовые
Фу'нкции ла'довыев музыке, значение отдельных звуков в
. Понятие Ф. л. наиболее разработано применительно к аккордам (гармонические функции) — обозначает роль аккордов в ладовой организации. Различают два рода общих функциональных значений аккордов — устойчивость (состояние покоя) и неустойчивость (состояние движения). В мажоро-минорной тональной системе устойчивость представлена функцией тоники (обозначение Т). По тонике, устою, определяется центр лада. Неустойчивых функций две — доминанта (D) и субдоминанта (S). Аккорды доминанты и субдоминанты строятся на звуках, находящихся в отношении наивысшего акустического родства к основному звуку тоники и лежащих квинтой выше (D) и квинтой ниже (S). Отсюда логическая противоположность функций D и S, усиливающаяся контрастом их звукового состава. Образующийся между основным звуком S и терцией D (вводным тоном лада) интервал тритона делает их тяготение к приме и терции тоники особенно сильным. Действие гармонических функций наиболее ярко проявляется в каденциях.
Предпосылки теории гармонических функций содержатся в работах Ж. Ф.
, М. Гауптмана, А. Эттингена. Идея «групп» Т, D и S разработана Н. А.
в его «Учебнике гармонии». Функциональную теорию гармонии в развитом её виде выдвинул в конце 19 в. Х.
. По Риману, все аккорды лада возникают как трансформации лишь трёх гармоний — тоники, доминанты и субдоминанты. Оригинальную концепцию Ф. л. («моментов» тяготения) создал советский теоретик Б. Л. Яворский. Важный вклад в развитие теории внёс советский музыковед Ю. Н. Тюлин. Теория гармонии, функций наиболее применима к анализу гармонии в музыке середины 18 — начала 20 вв.
Лит.:Риман Г., Упрощенная гармония или учение о тональных функциях аккордов, пер. с нем., М., 1901; Катуар Г. Д., Теоретический курс гармонии, ч, 1—2, М., 1924—25; Тюлин Ю. Н., Учение о гармонии, 3 изд., ч. 1, М., 1966; Способин И. В., Лекции по курсу гармонии, М., 1969; Imig R., Systeme der Funktionsbezeichnung in den Harmonielehren seit Hugo Riemann, Dьsseldorf, 1970.
Ю. Н. Холопов.
Функции (математ.)
Фу'нкциив математике, см.
.
Функции множества
Фу'нкции мно'жества,функции, сопоставляющие каждому множеству из некоторого класса множеств определённое число. Например, длина отрезка является Ф. м., определённой на классе всех отрезков на прямой (функцией отрезка).
Интеграл
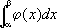
при заданной интегрируемой функции j(
x) также является функцией отрезка — интервала интегрирования [a, b]. Рассматривают также функции от областей на плоскости или в пространстве. Например, при заданном распределении плотностей масса, заключённая в данной области W, является функцией этой области. Понятие функции области — более гибкий аппарат для описания физических явлений, чем понятие функции точки, т.к. позволяет учитывать случаи, когда плотность физических величин в отдельных точках бесконечна (точечные источники и т.д.). Кроме того, это понятие более отвечает условиям физического эксперимента (при котором наблюдается не функция точки, а среднее от этой функции по некоторой малой области).
Понятие Ф. м. получило развитие в связи с построением теории интеграла Лебега, в которой приходится рассматривать не только функции от областей, но и функции от произвольных измеримых множеств. Одним из первых примеров такой Ф. м. является мера Лебега m(
Е) измеримого множества
Е(см.
). Эта Ф. м. вполне аддитивна, т. е. мера суммы любой конечной или счётной совокупности непересекающихся измеримых множеств есть сумма мер этих множеств. Наряду с лебеговской мерой множеств рассматривают др. меры, являющиеся неотрицательными вполне аддитивными Ф. м., определёнными на соответствующем классе множеств. Такие Ф. м. встречаются в общей теории интеграла. Ф. м.
f(
E) называют абсолютно непрерывной относительно некоторой меры m, если
f(
E) = 0 при m(
Е) = 0. Так, интеграл Лебега
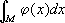
заданной суммируемой функции j(
x) по множеству
Мявляется вполне аддитивной абсолютно непрерывной (относительно меры Лебега) функцией от
М. Обратно, всякая вполне аддитивная абсолютно непрерывная Ф. м. может быть представлена в качестве интеграла Лебега от некоторой суммируемой функции j(
x). Важным примером Ф. м. являются
вероятностей.
Лит.:Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976; Халмош П., Теория меры, пер. с англ., М., 1953
Функции специальные
Фу'нкции специа'льные,см.
.
Функции (физиологич.)
Фу'нкции(от лат. functio — исполнение, совершение) физиологические, осуществление человеком, животными и растительными организмами различных отправлений, обеспечивающих их жизнедеятельность и приспособление к условиям окружающей среды, физиология изучает Ф. организма на молекулярном, клеточном, тканевом, органном и системном уровнях, а также на уровне целостного организма. К числу т. н. системных Ф. животного организма относятся, например, дыхательная, сердечно-сосудистая, пищеварительная, зрительная, слуховая, вестибулярная. Поскольку в основе любой Ф. лежит непрерывно идущий процесс
, их исследование предусматривает выяснение происходящих в организме (системе органов, отдельном органе, ткани и т.д.) физических, химических и структурных изменений. В связи с этим существенное значение приобретают работы в области
, изучающей процессы и движущие силы индивидуального развития организма —
.
Важную роль в комплексном изучении Ф. сыграл сравнительно-исторический метод, привнесённый в физиологию И. М.
, И. П.
, Н. Е.
. Трудами Л. А.
и его школы было создано оригинальное направление, изучающее физиологические, биохимические и структурные основы эволюции Ф., —
. В свою очередь исследования эволюции Ф. оказали влияние на изучение изменений Ф., наступающих в организме под влиянием различных факторов природного или искусственного происхождения (изменения климатических условий, двигательной активности, состава и свойств пищи, недостаток или избыток кислорода в воздухе, невесомость и многое др.), а также адаптации организма к условиям внешней среды (см.
). Изучение эволюции Ф. и особенно их приспособляемости к окружающей среде неразрывно связано с исследованием механизмов регуляции Ф. (см.
,
,
). Важный этап в изучении Ф. — созданная К. М.
и его школой концепция о взаимоотношениях
и внутренних органов (см.
). Развитие этой концепции позволило вплотную подойти к разработке проблемы управления деятельностью висцеральных, т. е. внутренностных, систем организма, основанной на представлении об этой деятельности как особой форме поведения. Имеется в виду, что Ф. висцеральных систем, как и поведение организма в целом, всегда адаптивны, развиваются в достаточно строгой последовательности отдельных составляющих их основу реакций, а также обладают способностью к «обучению» (совершенствованию). Исследования в этом направлении имеют своей задачей познание механизмов и закономерностей регуляции Ф. организма с целью активного вмешательства в процесс нормализации его жизнедеятельности в случае отклонений от нормы, в том числе и в экстремальных условиях.
Лит.см. при ст.
животных и человека.
В. Н. Черниговский,
К. А. Ланге.
Функции элементарные
Фу'нкции элемента'рные,см.
.
Функций теория
Фу'нкций тео'рия,раздел математики, в котором изучаются общие свойства
. Ф. т. распадается на две части: теория функций действительного переменного и теория функций комплексного переменного.
В «классическом» математическом анализе основным объектом изучения являются
, заданные на (конечных или бесконечных) интервалах и обладающие более или менее высокой степенью гладкости. Однако уже со 2-й половины 19 в. развитие математики всё настоятельнее стало требовать систематического изучения функций более общего типа. Основной причиной этого является то, что
последовательности непрерывных функций может быть разрывен. Иными словами, класс непрерывных функций оказывается незамкнутым относительно важнейшей операции анализа — предельного перехода. В связи с этим функции, определяемые при помощи таких классических средств, как тригонометрические ряды, часто оказываются разрывными или недифференцируемыми. По той же причине могут быть разрывны производные непрерывных функций и т.п. Наконец, дифференциальные уравнения, возникающие при рассмотрении физических задач, иногда не имеют решений в классе достаточно гладких функций, но имеют их в более широких классах функций (если надлежащим образом сообщить само понятие решения). Весьма важно, что именно эти обобщённые решения (см.
) и дают ответ на исходную физическую задачу. Эти и аналогичные им обстоятельства стимулировали создание Ф. т. действительного переменного.
Отдельные частные факты Ф. т. действительного переменного были открыты ещё в 19 в. (существование рядов непрерывных функций с разрывной суммой, примеры нигде не дифференцируемых непрерывных функций, не интегрируемых функций и т.п.). Однако эти факты воспринимались обычно как «исключения из правил» и не объединялись никакими общими схемами. Лишь в начале 20 в., когда в основу изучения функций были положены методы
, стала развиваться систематически современная Ф. т. действительного переменного.
Можно различить три направления в Ф. т. действительного переменного.
1) Метрическая Ф. т., где свойства функций изучаются при помощи меры (см.
) тех множеств, на которых эти свойства имеют место. В метрической Ф. т. с общих точек зрения изучаются интегрирование и дифференцирование функций (см.
,
,
), различными способами обобщается понятие
функциональных последовательностей, исследуется строение разрывных функций весьма широкого типа и т.п. Важнейшим классом функций, изучаемым в метрической Ф. т., являются
.
2) Дескриптивная Ф. т., в которой основным объектом изучения является операция предельного перехода (см.
).
3) Конструктивная Ф. т., изучающая вопросы изображения произвольных функций при помощи надлежащих аналитических средств (см.
).
О Ф. т. комплексного переменного см.
.
Лит.:Александров П. С., Введение в общую теорию множеств и функций, М. — Л., 1948; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976.
Функционал
Функциона'л,математический понятие, первоначально возникшее в
и означающее там переменную величину, зависящую от функции (линии) или от нескольких функций. Примерами Ф. являются площадь, ограниченная замкнутой кривой заданной длины, работа силового поля вдоль того или иного пути и т.д. С развитием функционального анализа термин «Ф.» стал пониматься в более широком смысле, а именно: как числовая функция, определённая на некотором линейном пространстве. См.
.
Функционализм
Функционали'зм,направление в зарубежном зодчестве 20 в., основанное на утверждении первичности функции (утилитарно-практические назначения) произведения архитектуры по отношению к его форме.
Во 2-й половине 19 в. принцип целесообразной формы, соединённой с этическим принципом правдивости выражения назначения и конструкции здания, был противопоставлен
, выявившему характерное для буржуазной культуры расщепление эстетического и утилитарного начал (на что указывали, в частности, английский критик Дж. Рескин и английский писатель, теоретик и дизайнер У. Моррис). Идеи целесообразной архитектуры развивались под влиянием теорий естественных наук (прежде всего эволюционной теории Ч. Дарвина). Природа стала рассматриваться как источник образцов совершенного приспособления формы к её назначению (американский скульптор и теоретик искусства Х. Гриноу и др.).
Систему идей американского «протофункционализма» конца 19 в. завершил архитектор Л. Г.
. В США эти идеи не получили непосредственные продолжения; лишь Ф. Л. Райт развивал на их основе теорию
.
Выдвинутая Салливеном формула «форму определяет функция» в середине 1920-х гг. была подхвачена западно-европейскими архитекторами, сторонниками
, полемически упростившими её содержание, сведя его к первичности утилитарного по отношению к эстетическому. Основанные на этой формуле принципы функциональности разрабатывались и пропагандировались Ле Корбюзье во Франции, а наиболее последовательно — архитекторами, связанными с
в Германии (В. Гропиус, Л. Мис ван дер Роэ, Х. Мейер и др.). Идеи целесообразного конструирования жизненной среды связывались с социальной утопией «жизнестроительства», создания материальных форм, которые могли бы способствовать «разумному преобразованию» капиталистического общества.
На структуру построек переносился принцип построения механизма; здания расчленялись в точном соответствии с последовательностью функциональных процессов, для которых они предназначались. Функции при этом анализировались на основе методов научной организации труда, в духе
. Принцип зонирования территории с выделением особого пространства для каждой из главных жизненных функций (их определяли так: «жить, работать, отдыхать, передвигаться») был перенесён и в область градостроительства. Рассудочные методы архитектурного творчества были доведены до крайней механистичности немецкими архитекторами, работавшими в конце 1920-х гг. в области муниципального жилищного строительства (Э. Май, Б. Таут, М. Вагнер).
Под влиянием
, представители которого решали задачи, во многом родственные поискам ведущих мастеров Ф., в творчестве западно-европейских архитекторов, связанных с Ф., во 2-й половине 1920-х гг. развивались демократические тенденции и элементы трезвого социального анализа. В условиях экономических трудностей конца 1920-х гг. идеи Ф. получили популярность у предпринимателей, их утопические идеи использовались социал-реформистскими политиками, но элементы социальной прогрессивности выхолащивались. Ф. утвердился во всех странах Западной Европы, а также в США и Японии. Однако наряду с распространением вширь он терял черты творческого метода, преобразуясь в некий «международный стиль», оперировавший внешними атрибутами целесообразной формы. Стремясь укрепить веру в трезвую целеустремлённость направления, приверженцы и стали называть его «Ф.» (швейцарский теоретик архитектуры З. Гидион внедрил этот термин как характеризующий всё «нетрадиционное» зодчество 1920—30-х гг.).
Повсеместное, не зависящее от условий среды и климата насаждение форм и приёмов, возникших в конкретных условиях Германии и Франции, вело к противоречиям с самим принципом рационального подхода к архитектуре. Архитекторы Финляндии (А. Аалто и др.), Швеции (С. Маркелиус и др.) уже в 1930-е гг., опираясь на метод Ф., стали разрабатывать приёмы, отвечающие национальной специфике своих стран. Это положило начало развитию региональных архитектурных школ, развивавшихся в рамках Ф., «международный стиль» стал распадаться. Разочаровавшись в иллюзиях «великой социальной миссии архитектуры», объединявших зачинателей Ф., его приверженцы стали отходить от анализа социальных проблем, что ещё более подрывало позиции Ф.
После 2-й мировой войны 1939—45 влияние архитектуры Ф. возродилось при восстановлении разрушенных городов, однако единство «международного стиля» распалось окончательно. Против основной доктрины Ф. выступил один из прежних его лидеров Л.
, а также приверженцы
, возродившегося
и возврата к историческим традициям.
В современной сов. архитектурной теории преобладает тенденция к внимательному изучению творческого наследия мастеров Ф. (в особенности тех концепций, которые были связаны с проблематикой советского зодчества 1920-х гг.); вместе с тем подвергаются критике социально-утопические воззрения представителей Ф., многие из которых надеялись преобразовать капиталистическое общество с помощью архитектуры.
Лит.:Всеобщая история архитектуры, т. 11, М., 1973; Мастера архитектуры об архитектуре, М., 1972; Гропиус В., Границы архитектуры (пер. с нем.), М., 1971; Sfaellos C. A., Le fonctionnalisme dans l'architecture contemporaine, P., 1952; Zurko E. R. de, Origins of functionalist theory, N. Y., 1957.
А. В. Иконников.
Функциональная психология
Функциона'льная психоло'гия,направление, исследующее психические явления с точки зрения их функции в приспособлении организма к среде. Возникла в конце 19 в. под влиянием
, способствовавшего переходу от поэлементного анализа сознания в структурной психологии В.
— Э.
к изучению роли сознания при решении индивидом различных задач. В Ф. п. имелось несколько течений. В европейских странах естественнонаучной трактовки психических функций придерживались Т.
(Франция), Н. Н.
(Россия), Э.
(Швейцария), идеалистической трактовки — К.
и представители т. н.
(Германия). В США сложился другой вариант Ф. п., восходящий к У.
и представленный двумя школами: чикагской (Дж.
, Дж. Энджелл, Г. Карр) и колумбийской (Р.
). Психология понималась как наука о функциях (или «деятельностях») сознания в процессе адаптации организма к изменяющемуся природному и социальному окружению. Область исследований психологии охватила не только сознание, но и поведение (приспособительные действия), его мотивы, механизмы научения и др. Сторонники этого направления внесли существенный вклад в экспериментальную психологию. Однако дуализм в понимании отношений между телесными и психическими функциями, телеологический взгляд на сознание как целенаправленно действующую сущность привели к тому, что это направление утратило научное влияние. В 20-х гг. американская Ф. п. была оттеснена
.
Лит.:Ярошевский М. Г., История психологии, М., 1966; Wood worth R. S., Dynamic psychology, N. Y., 1918; Carr Н. A., Psychology. A study of mental activity, N. Y., 1927; Boring E. G., A history of experimental psychology, 2 ed., N. Y., 1950; Misiak Н., Sexton U., History of psychology, 2 ed., N. Y. — L., 1968.
М. Г. Ярошевский.
Функциональная система
Функциона'льная систе'ма,важный объект математической кибернетики, представляющий собой множество функций с некоторым набором операций, применяемых к этим функциям. Ф. с. является формализованным отражением следующих главных особенностей реальных и абстрактных управляющих систем: функционирования (в Ф. с. это функции), правил построения более сложных управляющих систем из заданных и описания функционирования сложных систем по функционированию их компонент (последние два момента отражены в операциях Ф. с.). Примерами Ф. с. являются
, алгебры автоматов, алгебры рекурсивных функций и др. Ф. с. обладает определённой спецификой, состоящей в рассмотрении задач и подходов, возникающих при исследовании Ф. с. с позиций математической кибернетики, математической логики и алгебры. Так, с позиций математической кибернетики Ф. с. рассматриваются как языки, описывающие функционирование сложных систем. С позиций математической логики Ф. с. рассматриваются как модели логик, т. е. как системы высказываний с логическими операциями над ними. С точки зрения алгебры Ф. с. представляют собой т. н. алгебраические системы. Важной особенностью Ф. с., выделяющей их из общего класса алгебраических систем, является их содержательная связь с реальными кибернетическими моделями управляющих систем. Эта связь, с одной стороны, определяет гамму существенных требований, которые накладываются на Ф. с., а с другой стороны, порождает серию важных задач, имеющих как теоретическое, так и прикладное значение. Первоначально изучение Ф. с. началось с конкретных моделей логики, одной из первых среди которых была двузначная логика. Затем был изучен целый ряд конкретных Ф. с., многообразие которых и составляет содержание понятия Ф. с. Проблематика Ф. с. обширна и имеет много общего с проблематикой многозначных логик. К числу важнейших задач для Ф. с. относятся т. н. задачи о полноте, о сложности, выражения одних функций через другие, о тождественных преобразованиях, о синтезе и анализе и др., решение которых достаточно продвинуто применительно к целому ряду конкретных Ф. с.
Лит.:Яблонский С. В., Функциональные построения в к-значной логике, «Труды Матем. института АН СССР», 1958, т. 51, с. 5—142; его же, Обзор некоторых результатов в области дискретной математики, «Информационные материалы», 1970, № 5 (42), с. 5—15; Проблемы кибернетики, в. 1, М., 1958.
В. Б. Кудрявцев.
Функциональная школа (в музыке)
Функциона'льная шко'лав музыке, см.
.
Функциональная школа (этнографич.)
Функциона'льная шко'ла,функционализм, направление в буржуазной этнографии, сложившееся в 1920-х гг. главным образом в Великобритании и её бывших доминионах. Основатели и главные теоретики — Б. К.
и А. Р.
. В отличие от
и
Малиновский и представители Ф. ш. (Р. Фёрт, Э. Эванс-Притчард и др.) рассматривали культуру каждого народа не как механическое сочетание пережитков и заимствований, а как систему «институтов» (норм, обычаев, верований), призванных выполнить необходимые общественные «функции» (отсюда название школы). Нарушение какой-либо функции приводит к разрушению социального организма в целом. Теоретические исследования функционалисты сочетали со сбором этнографических материалов. Метод последователей Ф. ш. был односторонним: они учитывали лишь «синхронное» функционирование культуры, игнорируя необходимость исторического подхода к проблемам общественного развития. Исследования Ф. ш. были использованы брит. колониальной администрацией («косвенное управление» через местных вождей, консервация архаических черт культуры). Метод и теоретические построения Ф. ш. в социологии развиты и частично пересмотрены сторонниками
, в этнографии — структуралистами (Э. Лич, В. Тернер).
Лит.:Этнологические исследования за рубежом, М., 1973; Malinowski В., А scientific theory of culture and other essays N. Y., 1960; Radcliffe-Brown A. R., Structure and function in primitive society, L., 1952; его же. Method in social anthropology, Chi., 1958.
С. А. Токарев.
Функциональная электроника
Функциона'льная электро'ника,функциональная микроэлектроника, молекулярная электроника, встречающееся в научно-технической литературе название направления
. Ф. э. охватывает вопросы получения континуальных (непрерывных) комбинированных сред с наперёд заданными свойствами и создания различных электронных устройств методом физической интеграции, т. е. использования таких физических принципов и явлений, реализация которых позволяет получить компоненты со сложным схемотехническим или системотехническим функциональным назначением (в отличие от технологической интеграции — конструирования
на основе функционально простых элементов типа транзисторов, диодов, резисторов и т.д.).
Функциональное пространство
Функциона'льное простра'нство,совокупность функций с определённым для них тем или иным способом понятием расстояния или, более общо, близости. Ф. п., содержащее вместе с каждыми двумя элементами
f
1и
f
2все их линейные комбинации a
f
1+ b
f
2, где a и b — действительные или комплексные числа, называемые линейным Ф. п. Примером линейного Ф. п. является пространство
С(
a,
b) всех непрерывных функций на некотором отрезке [
а,
b] с расстоянием r(
f
1,
f
2) между двумя функциями, определяемым формулой
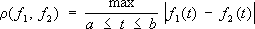
.
Важнейшие конкретные
, рассматриваемые в
, являются Ф. п.
Функциональные уравнения
Функциона'льные уравне'ния,весьма общий класс уравнений, в которых искомой является некоторая функция. К Ф. у. по существу относятся
,
, уравнения в конечных разностях (см.
); следует, однако, отметить, что название «Ф. у.» обычно не относят к уравнениям этих типов. Под Ф. у. в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Ф. у. можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций [например, Ф. у. (
x) =
f(—
x) характеризует класс чётных функций, Ф. у.
f(
x+ 1) =
f(
x) — класс функций, имеющих период 1, и т.д.].
Одним из простейших Ф. у. является уравнение
f(
x+
у) =
f(
x) +
f(
y). Непрерывные решения этого Ф. у. имеют вид
f(
x) =
Cx. Однако в классе разрывных функций это Ф. у. имеет и иные решения. С рассмотренным Ф. у. связаны
f(
x+
у) =
f(
x)
f(
y),
f(
xy) —
f(
x) +
f(
y),
f(
xy) =
f(
x)
f(
y),
непрерывные решения которых имеют соответственно вид
e
Cx,
Cln
x,
x
a(
x> 0). Т. о., эти Ф. у. могут служить для определения показательной, логарифмической и степенной функций.
В теории
Ф. у. часто применяются для введения новых классов функций. Например, двоякопериодические функции характеризуются Ф. у.
f(
z+
а) =
f(
z) и
f(
z+
b) =
f(
z),
— Ф. у.
f(
s
a
z) =
f(
z), где {
s
a} — некоторая группа дробно-линейных преобразований. Если функция известна в некоторой области, то знание для неё Ф. у. позволяет расширить область определения этой функции. Например, Ф.
у.
f(
x+ 1) =
f(
x) для периодических функций позволяет определить их значение в любой точке по значениям на отрезке [0, 1]. Этим часто пользуются для аналитического продолжения функций комплексного переменного. Например, пользуясь Ф. у. Г (
z+ 1) =
zГ (
z) и зная значения функции Г (
z) (см.
) в полосе 0 Ј Re
zЈ 1, можно продолжить её на всю плоскость
z.
Условия симметрии, имеющиеся в какой-либо физической задаче, обусловливают определённые законы преобразования решений этой задачи при тех или иных преобразованиях координат. Этим определяются Ф. у., которым должно удовлетворять решение данной задачи. Значение соответствующих Ф. у. во многих случаях облегчает нахождение решений.
Решения Ф. у. могут быть как конкретными функциями, так и классами функций, зависящими от произвольных параметров или произвольных функций. Для некоторых Ф. у. общее решение может быть найдено, если известны одно или несколько его частных решений. Например, общее решение Ф. у.
f(
x) =
f(
ax) имеет вид j[w(
x)], где j(
x) — произвольная функция, а w(
x) — частное решение этого Ф. у. Для решения Ф. у. их во многих случаях сводят к дифференциальным уравнениям. Этот метод даёт лишь решения, принадлежащие классу дифференцируемых функций.
Другим методом решения Ф. у. является метод
. Этот метод даёт, например, решение уравнения Абеля
f[a(
x)] =
f(
x) + 1 [где a(
x) — заданная функция] и связанного с ним уравнения Шрёдера
f[a(
x)] =
cf(
x). А. Н.
доказал, что если a(
х) — аналитическая функция, то уравнение Абеля имеет аналитическое решение. Эти результаты, нашедшие применение в теории групп Ли (см.
), привели в дальнейшем к созданию теории итераций аналитических функций. В некоторых случаях уравнение Абеля решается в конечном виде. Например, Ф. у.
f(
x
n) =
f(
x) + 1 имеет частное решение
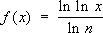
.
Лит.:Ацель Я., Некоторые общие методы в теории функциональных уравнений одной переменной. Новые применения функциональных уравнений, «Успехи математических наук», 1956, т. 11, в. 3, с. 3—68.
«Функциональный анализ и его приложения»
«Функциона'льный ана'лиз и его' приложе'ния»,научный журнал Отделения математики АН СССР, публикующий оригинальные работы по актуальным вопросам функционального анализа и его приложений, а также информационные материалы. Издаётся в Москве с 1967. Ежегодно выходит 1 том, состоящий из 4 выпусков. Тираж (1977) около 1500 экз.
Функциональный анализ (математ.)
Функциона'льный ана'лиз,часть современной математики, главной задачей которой является изучение бесконечномерных пространств и их отображений. Наиболее изучены линейные пространства и линейные отображения. Для Ф. а. характерно сочетание методов классического анализа, топологии и алгебры. Абстрагируясь от конкретных ситуаций, удаётся выделить аксиомы и на их основе построить теории, включающие в себя классические задачи как частный случай и дающие возможность решать новые задачи. Сам процесс абстрагирования имеет самостоятельное значение, проясняя ситуацию, отбрасывая лишнее и открывая неожиданные связи. В результате удаётся глубже проникнуть в сущность математических понятий и проложить новые пути исследования.

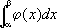 при заданной интегрируемой функции j(
x) также является функцией отрезка — интервала интегрирования [a, b]. Рассматривают также функции от областей на плоскости или в пространстве. Например, при заданном распределении плотностей масса, заключённая в данной области W, является функцией этой области. Понятие функции области — более гибкий аппарат для описания физических явлений, чем понятие функции точки, т.к. позволяет учитывать случаи, когда плотность физических величин в отдельных точках бесконечна (точечные источники и т.д.). Кроме того, это понятие более отвечает условиям физического эксперимента (при котором наблюдается не функция точки, а среднее от этой функции по некоторой малой области).
при заданной интегрируемой функции j(
x) также является функцией отрезка — интервала интегрирования [a, b]. Рассматривают также функции от областей на плоскости или в пространстве. Например, при заданном распределении плотностей масса, заключённая в данной области W, является функцией этой области. Понятие функции области — более гибкий аппарат для описания физических явлений, чем понятие функции точки, т.к. позволяет учитывать случаи, когда плотность физических величин в отдельных точках бесконечна (точечные источники и т.д.). Кроме того, это понятие более отвечает условиям физического эксперимента (при котором наблюдается не функция точки, а среднее от этой функции по некоторой малой области).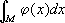 заданной суммируемой функции j(
x) по множеству
Мявляется вполне аддитивной абсолютно непрерывной (относительно меры Лебега) функцией от
М. Обратно, всякая вполне аддитивная абсолютно непрерывная Ф. м. может быть представлена в качестве интеграла Лебега от некоторой суммируемой функции j(
x). Важным примером Ф. м. являются
вероятностей.
заданной суммируемой функции j(
x) по множеству
Мявляется вполне аддитивной абсолютно непрерывной (относительно меры Лебега) функцией от
М. Обратно, всякая вполне аддитивная абсолютно непрерывная Ф. м. может быть представлена в качестве интеграла Лебега от некоторой суммируемой функции j(
x). Важным примером Ф. м. являются
вероятностей.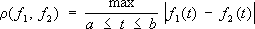 .
.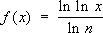 .
.