Большая Советская Энциклопедия (ФЕ)
ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ФЕ) - Чтение
(стр. 22)
|
Автор:
|
БСЭ |
|
Жанр:
|
Энциклопедии |
|
-
Читать книгу полностью
(892 Кб)
- Скачать в формате fb2
(7,00 Мб)
- Скачать в формате doc
(367 Кб)
- Скачать в формате txt
(343 Кб)
- Скачать в формате html
(7,00 Мб)
- Страницы:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30
|
|
Фердинанд VII
Фердина'нд VII(Fernando) (13.10.1784, Сан-Ильдефонсо, – 29.9.1833, Мадрид), король Испании в 1808 и 1814–33. Стал королём 19 марта 1808 в результате свержения восставшим народом временщика Годоя и отречения от престола Карла IV (отец Ф. VII). Вскоре, используя раздоры в королевской семье, Наполеон I, войска которого весной 1808 оккупировали Испанию, добился отречения от исп. престола Ф. VII (10 мая 1808), возведя на престол своего брата Жозефа Бонапарта. В 1808–14 Ф. VII жил во Франции, Вернулся в Испанию после падения французского господства в марте 1814. Окружив себя
,ликвидировал завоевания испанской революции 1808–14. В условиях начавшейся в 1820 новой революции вынужден был признать радикальную конституцию 1812 и в то же время возглавил лагерь контрреволюции. После подавления в 1823 революции французскими интервентами восстановил абсолютистский режим в Испании.
Фердман Давид Лазаревич
ФердманДавид Лазаревич [25.12.1902(7.1.1903), г. Тересполь, ныне Люблинское воеводство, Польша, – 11.1.1970, Киев], советский биохимик, член-корреспондент АН СССР (1946) и АН УССР (1939). В 1925 окончил Харьковский институт народного образования. В 1925–31 и 1943–70 работал в институте биохимии АН УССР и одновременно (в 1944–70) профессор Киевского университета. В 1930–43 – в Харьковском медицинском институте. Основные труды по обмену фосфорных соединений, образованию и устранению аммиака в мышцах при их деятельности, а также обмену веществ в мышцах при их заболевании. Обнаружил глутамин в тканях животных и определил его роль. Награжден орденом Ленина и медалями.
Соч.: Биохимия фосфорных соединений, К., 1935; Обмен фосфорных соединений, М. – Л., 1940; Биохимия заболеваний мышц, К., 1953; Биохимия, 3 изд., М., 1966.
Ференигинг
Фере'нигинг,Веренигинг, Феринихинг (Vereeniging). город в ЮАР, в провинции Трансвааль, на берегу р. Вааль. 169,6 тыс. жителей (1970). Ж.-д. узел. Важный центр добычи каменного угля, чёрной металлургии. Трубопрокатные заводы, производство горного оборудования, с.-х. машин; химическая промышленность. Ф. основан в 1892.
Ференци Карой
Фе'ренци(Ferenezy) Карой (8.2.1862, Вена, – 18.3.1917, Будапешт), венгерский живописец. Учился в Риме (1884), Мюнхене и Париже в Академии Жюлиана (1887–89). Член колонии художников в Надьбанье (ныне в Румынии; 1896–1906). Профессор будапештской АХ (с 1905). Испытал влияние Ж.
.Один из ведущих мастеров венгерской пленэрной живописи конца 19 – начала 20 вв., Ф. стремился к декоративной насыщенности колорнстических и композиционных решений. Писал жанровые сцены («Мальчики, бросающие камни», 1890, Венгерская национальная галерея, Будапешт), пейзажи, многочисленные композиции на библейские и евангельские темы.
Лит.:Genthon 1., Ferenezy Karoly, Bdpst, 1963.
Фереос Констандинос
Фере'ос(Pheraios) Констандинос (около 1757–24.6.1798), греческий революционер-демократ, поэт. См.
К.
Ферма великая теорема
Ферма' вели'кая теоре'ма,утверждение П.
отом, что
x
n
+ y
n
= z
n
,где
n –целое число, большее двух, не имеет решений в целых положительных числах. Ф. в. т. установлена для ряда частных значений
n,однако доказательства её в общем случае не получено. Несмотря на простоту формулировки Ф. в. т., полное её доказательство, по-видимому, требует создания новых и глубоких методов в теории диофантовых уравнений. Нездоровый интерес к доказательству этой теоремы среди неспециалистов в области математики был в своё время вызван большой международной премией, аннулированной ещё в конце 1-й мировой войны 1914–18.
Лит.:Dickson L. Е., History of the theory of numbers, v. 1–3, N. Y., 1934; Landau Е., Aus der algebraischen Zahlentheorie und ьber die Fermatsche Vermutung, Lpz., 1927 (Vorlesungen uber Zahlentheorie, Bd 3).
Ферма животноводческая
Фе'рма животново'дческаяв СССР, подразделение с.-х. предприятия, занимающееся разведением с.-х. животных и производством животноводческой продукции; форма организации общественного
.Ф. ж. может входить в состав более крупного внутрихозяйственного подразделения (отделение, комплексная бригада, производственный участок) или быть самостоятельной производственной единицей. На территории фермы имеются: комплекс животноводческих помещений, здания и постройки вспомогательного назначения, инженерно-технические сооружения, дороги и коммуникации. Характер и структура строений зависят от размера Ф. ж. и особенностей содержания определённых видов и групп с.-х. животных. Например, на крупной молочной ферме размещены: коровники, доильно-молочный блок, пункт искусственного осеменения, родильное отделение с телятником-профилакторием, кормоприготовительное отделение, сенажные и силосные траншей или башни, помещения и навесы для хранения кормов, административно-бытовые и др. здания и сооружения вспомогательного назначения. Ф. ж. имеют машины и оборудование для механизации производственных процессов.
С.-х. животных обслуживают работники соответствующих профессий, состоящие в штате Ф. ж. производство кормов организуют специализированные бригады, отряды, звенья по кормопроизводству или тракторно-полеводческие бригады хозяйства. Укреплению
способствует создание вблизи Ф. ж. высокопродуктивных орошаемых культурных пастбищ.
Историческая справка. Образование первых Ф. ж. связано с организацией
.Совхозные фермы сыграли большую роль в формировании Ф. ж. в
,которые использовали опыт совхозов по организации Ф. ж., покупали у них племенных животных и т.д. Создание Ф. ж. в совхозах и колхозах имело важное экономическое значение. В резолюции Июньского пленума ВКП (б) (1934) «Об улучшении и развитии животноводства» отмечалось, что товарные Ф. ж. стали основой подъёма животноводства, улучшения качества скота и роста товарной продукции. Длительное время в хозяйствах создавались сравнительно небольшие Ф. ж. разного производственного направления. По мере укрепления материально-технической базы колхозов и совхозов, углубления специализации и концентрации производства размеры Ф. ж. увеличивались. Ускорению этого процесса способствовали решения Мартовского пленума ЦК КПСС (1965), 24-го съезда партии (1971), постановление ЦК КПСС и Совета Министров СССР «О развитии производства продуктов животноводства на промышленной основе» (16 апреля 1971), в соответствии с которыми совхозы и колхозы расширяют и реконструируют действующие Ф. ж., строят крупные фермы промышленного типа с высокой степенью механизации, прогрессивными системами содержания животных, современной технологией производства продукции. Решения 25-го съезда КПСС (1976), постановление ЦК КПСС «О дальнейшем развитии специализации и концентрации сельскохозяйственного производства на базе межхозяйствснной кооперации и аграрно-промышленной интеграции» (июнь 1976) предусматривают дальнейшее углубление специализации и перевод животноводческих отраслей на индустриальную основу, в результате чего Ф. ж. по уровню организации производства и труда постепенно приблизятся к промышленным предприятиям (см.
,
)
.
Планировка Ф. ж. Рациональное размещение ферм на территории хозяйства обеспечивает минимальные затраты на транспортировку кормов, вывоз продукции, органических удобрений, доставку обслуживающего персонала и т.п., поэтому при выборе места для строительства Ф. ж. учитывают расположение кормовых угодий, водных источников, дорог, скотопрогонов, населённых пунктов. В соответствии с требованиями по охране окружающей среды от загрязнения для Ф. ж. отводят земельный участок, пригодный по естественым и ветеринарно-санитарным условиям. Способ застройки Ф. ж. зависит от проектируемых размеров и технологии производства продукции. Для крупных ферм промышленного типа характерна сблокированная застройка, для мелких – павильонная. Сблокированные строения более рациональны и эффективны: сокращаются площади застройки, протяжённость инженерных коммуникаций и дорог, уменьшаются капитальные вложения в расчёте на голову скота. Животноводческие постройки располагают ниже жилых и культурно-бытовых зданий. Территорию Ф. ж. огораживают и озеленяют; у входа (въезда) оборудуют санпропускник и дезбарьер.
Типы Ф. ж. По назначению фермы делятся на племеные и товарные. На племенных Ф. ж. воспроизводят племенной скот для улучшения стад товарных ферм; на товарных – производят животноводческую продукцию. В соответствии со специализацией колхозов и совхозов создают Ф. ж. по производству молока, говядины, свинины, баранины, шерсти, яиц и т.п. В связи с углублением внутриотраслевой специализации в животноводстве скотоводческого хозяйства вместо смешанных ферм с законченным оборотом стада организуют специализированные молочные фермы, на которых, кроме коров, содержат только телят в период выпойки молоком; одновременно создают специализированные молочные фермы, по выращиванию ремонтного молодняка (для комплектования молочного стада), по выращиванию и откорму сверхремонтного молодняка. В свиноводческих хозяйствах вместо ферм с законченным производственным циклом создают репродукторные, специализирующиеся главным образом на получении поросят и выращивании их до 4
мес,и откормочные фермы. Узкоспециализированные фермы имеются и в др. животноводческих отраслях.
Размеры Ф. ж. характеризуются объёмом валовой или товарной продукции и численностью поголовья. Применительно к конкретным условиям определяют оптимальные размеры Ф. ж., при которых обеспечивается наиболее высокий уровень рентабельности производства. Для молочных ферм они колеблются (по природно-экономическим зонам) от 200–400 до 600–1200 коров; для свиноводческих репродукторных – от 100 до 600 основных свиноматок, откормочных – от 10 тыс. до 16 тыс. свиней единовременного откорма, племенных – 100–200 основных свиноматок; для товарных овцеводческих – от 2 тыс. до 24 тыс. овец.
Содержание животных на Ф. ж. В зависимости от технологии производства, климатических и хозяйственных условий (обеспеченность кормами и др.) применяют различные способы
.На крупных молочных фермах промышленного типа коров содержат на привязи или беспривязно (группами, на глубокой подстилке или в боксах). Группы коров формируют с учётом периода лактации, величины суточного удоя и физиол. состояния животных, что позволяет производительно использовать
,организовать нормированное кормление. Содержание ремонтных тёлок на специализированных фермах организуют в соответствии с особенностями их развития в разные возрастные периоды: для тёлок до 3
мес –индивидуальное клеточное, от 3 до 9
мес –групповое станочное, старше 9
мес –то же, что на молочных фермах. Размер групп зависит от возраста тёлок и степени механизации рабочих процессов. Молодняк, выращиваемый на мясо, в возрасте до 3
месобычно размещают в индивидуальных клетках, после чего до 12
мессодержат беспривязно в групповых станках; на стадии заключительного откорма животные находятся без привязи (группами) на щелевых полах или открытых откормочных площадках с навесами. Содержание свиней организуют с учётом их физиологического состояния, по возрастным группам. Подсосных свиноматок с поросятами размещают в индивидуальных станках с раздельными кормушками. Поросят-отъёмышей, ремонтный молодняк, откормочное поголовье содержат в станках, группами, размер которых определяется возрастом животных, организацией их кормления и др. факторами. Способы содержания овец, лошадей, зверей и др. зависят от особенностей технологии производства продукции, климатических и хозяйственных условий. На птицеводческих фермах применяют клеточное и напольное содержание птицы.
Организация труда. Основная форма организации труда на Ф. ж. – постоянная производственная бригада. Животноводческие бригады могут быть отраслевыми (обслуживать разные группы животных одного вида), специализированными (обслуживать одну группу животных) и комплексными (выполнять все работы по уходу за животными). На крупных свиноводческих фермах распространена раздельно-цеховая организация производства и труда (в соответствии с размещением групп животных по цехам фермы). На овцеводческих фермах животных распределяют по отарам, которые обслуживают чабанские бригады. Формы внутрибригадной организации труда: индивидуальная – определённую группу животных обслуживает один работник (на мелких фермах), и групповая – поголовье закрепляют за группой (звеном) животноводов (на фермах промышленного типа). Труд работников Ф. ж. оплачивается в соответствии с их квалификацией, объёмом выполненных работ, количеством и качеством полученной продукции (см.
,
)
.
На Ф. ж. механизируют транспортировку, приготовление и раздачу кормов, водоснабжение и поение животных, доение коров, первичную обработку и переработку молока, стрижку овец, сбор яиц, уборку навоза из животноводческих помещений, доставку его в навозохранилища и др. рабочие процессы (см.
)
.В условиях привязного содержания коров доят в стойлах или на доильных установках; при беспривязном и беспривязно-боксовом – в доильных залах на стационарных групповых установках («Елочка», «Тандем», «Карусель» и др.). На механизированных фермах применяют двукратное доение коров, что обеспечивает рациональное использование доильных установок и рост производительности труда. Для раздачи кормов и уборки навоза применяют стационарные средства механизации или тракторы. На крупных Ф. ж. с комплексной механизацией рабочих процессов действует система взаимосвязанных и согласованных по производительности электрифицированных и автоматизированных поточных линий доения коров и обработки молока, приготовления и раздачи кормов, удаления навоза и др.
Лит.:Материалы XXV съезда КПСС, М., 1976; Проблемы аграрной политики КПСС на современном этапе, т. 1–2, М., 1975; Организация и планирование производства в сельскохозяйственных предприятиях, М., 1974; Организация производства в совхозах и колхозах, М., 1973.
С. И. Грядов.
Ферма малая теорема
Ферма' ма'лая теоре'ма,одна из основных теорем теории чисел, состоящая в том, что если
р –простое число и
а –целое число, не делящееся на
р,то
a
p-1
–1 делится на
р,т. е.
a
p-1є1(mod
p)
.Теорему высказал без доказательства П.
первое доказательство дал Л.
.
Ферма принцип
Ферма' при'нцип,основной принцип
.Простейшая форма Ф. п. – утверждение, что луч света всегда распространяется в пространстве между двумя точками по тому пути, по которому время его прохождения меньше, чем по любому из всех др. путей, соединяющих эти точки. Время прохождения светом расстояния
l, заполненного средой с
n, пропорционально
S;
S =1•
nдля однородной среды, а при переменном
n
.Поэтому можно сказать, что Ф. п. есть принцип наименьшей оптической длины пути. В первоначальной формулировке самого П.
(около 1660) Ф. п. имел смысл наиболее общего закона распространения света, из которого следовали все (к тому времени уже известные) законы геометрической оптики: для однородной среды он приводит к закону прямолинейности светового луча (в соответствии с геометрическим положением о том, что прямая есть кратчайшее расстояние между двумя точками), а для случая падения луча на границу различных сред из Ф. п. можно получить законы
и
.В более строгой формулировке Ф. п. представляет собой вариационный принцип, утверждающий, что реальный луч света распространяется от одной точки к другой по линии, по которой время его прохождения экстремально или одинаково по сравнению с временами прохождения по всем др. линиям, соединяющим эти точки. Это означает, что оптическая длина пути луча может быть не только минимальной, но и максимальной либо равной всем остальным возможным путям, соединяющим указанные точки. Примерами минимального пути служат упомянутые распространение света в однородной среде и прохождение светом границы двух сред с разными показателями преломления
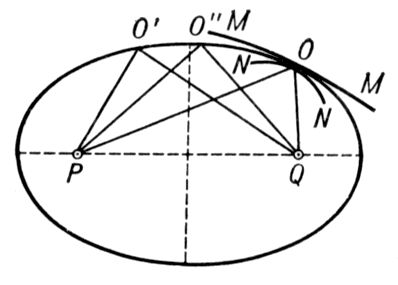
n.Все три случая (минимальности, максимальности и стационарности пути) можно проиллюстрировать, анализируя отражение луча света от вогнутого зеркала (
рис.
). К принципу Ферма: действительный путь света соответствует экстремальному времени распространения. Если зеркало имеет форму
вращения, а свет распространяется от одного его фокуса
Рк другому
Q(причём путь без отражения невозможен), то оптическая длина пути луча
PO' + O'Qпо свойствам эллипсоида равна всем остальным возможным, например
PO''+
О''
Q; если на пути между теми же точками свет отражается от зеркала меньшей, чем у эллипсоида, кривизны (
MM)
,реализуется минимальный путь, если же большей (зеркало
NN)
–максимальный. Условие экстремальности оптической длины пути сводится к требованию, чтобы была равна нулю вариация от интеграла
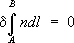 (см.
), где
Аи
В –точки, между которыми распространяется свет. Это выражение и представляет собой математическую формулировку Ф. п. В волновой теории света Ф. п. представляет собой предельный случай
и применим, когда можно пренебречь
(когда длина световой волны достаточно мала по сравнению с характерными для задачи размерами): рассматривая лучи как нормали к волновым поверхностям, легко показать, что при всяком распространении света оптической длины их путей будут иметь экстремальные значения. Во всех случаях, когда необходимо учитывать дифракцию, Ф. п. перестаёт быть применимым.
Лит.:Fermat P. de, CEuvres, t. 1–4, P., 1891–1912; Ландсберг Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики); Крауфорд Ф., Волны, М., 1974 (Берклеевский курс физики, т. 3); Борн М., Вольф Э., Основы оптики, пер. с англ., 2 изд., М., 1973.
А. П. Гагарин.
К принципу Ферма: действительный путь света соответствует экстремальному времени распространения.
Ферма Пьер
Ферма'(Fermat) Пьер (17.8.1601, Бомон-де-Ломань, – 12.1.1665, Кастр), французский математик. По профессии юрист: с 1631 был советником парламента в Тулузе. Автор ряда выдающихся работ, большинство из которых было издано после смерти Ф. его сыном, – «Различные сочинения» (1679); при жизни Ф. полученные им результаты становились известны учёным благодаря переписке и личному общению. Ф. является одним из создателей теории чисел, где с его именем связаны 2 знаменитые теоремы:
и
.В области геометрии Ф. в более систематической форме, чем Р.
,развил метод координат, дав уравнения прямой и линий второго порядка и наметив доказательство положения о том, что все кривые второго порядка – конического сечения. В области метода бесконечно малых систематически изучил процесс дифференцирования, дал общий закон дифференцирования степени и применил этот закон к дифференцированию дробных степеней. В подготовке современных методов дифференциального исчисления большое значение имело создание им правила нахождения экстремумов. Ф. дал общее доказательство правильности закона интегрирования степени, подмеченного на частных случаях уже ранее. Он распространил его и на случай дробных и отрицательных степеней. В трудах Ф., таким образом, получили систематическое развитие оба основных процесса метода бесконечно малых, однако он, как и его современники, прошёл мимо связи между операциями дифференцирования и интегрирования. Эта связь была установлена несколько позднее (в систематической форме) Г.
и И.
.Своими работами Ф. оказал большое влияние на дальнейшее развитие математики. В области физики с именем Ф. связано установление основного принципа геометрической оптики (см.
)
.
Соч.: CEuvres, t. 1–4, P., 1891–1912.
Лит.:Бурбаки Н., Элементы математики, [кн. 8]. Очерки по истории математики, пер. с франц., М., 1963 [лит.]; История математики с древнейших времён до начала XIX столетия, т, 2, М., 1970. П. Ферма.
Ферма (технич.)
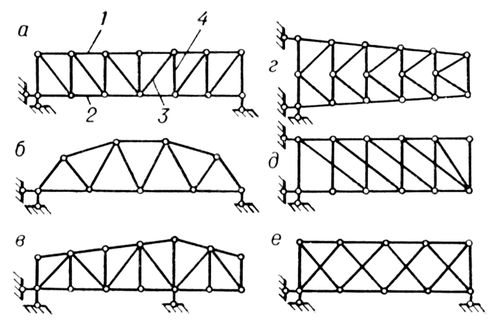
Ферма'(франц. ferme, от лат. firmus – крепкий, прочный), несущая конструкция, состоящая из прямолинейных стержней, узловые соединения которых при расчёте условно принимаются шарнирными. Ф. применяют главным образом в строительстве (покрытия зданий, пролётные строения мостов, мачты, опоры линий электропередачи, гидротехнические затворы и др.), а также в качестве несущих конструкций машин и механизмов. По виду материала различают металлические, железобетонные, деревянные и комбинированные (например, металлодеревянные) Ф. Тип Ф. и её очертания (
рис.
) определяются назначением здания или сооружения, видом покрытия, способом опирания Ф. и т.д. Узлы Ф., хотя и считаются шарнирными, практически обладают той или иной степенью жёсткости. При проектировании Ф., как правило, обеспечивается узловое приложение внешней нагрузки (например, прогоны покрытия здания опираются на Ф. в узлах верхнего пояса, балки подвесных кранов крепятся к узлам нижнего пояса и т.д.). Допущения о шарнирном соединении узлов и узловом приложении нагрузки позволяют учитывать при расчёте Ф. только осевые продольные усилия в стержнях (при этом в поперечных сечениях стержней возникают равномерно-распределённые напряжения, позволяющие наиболее эффективно использовать материал). Усилия в стержнях статически определимых плоских Ф. (см.
) определяют из уравнений статики, пространственных – как правило, путём расчленения на плоские. Статически неопределимые Ф. (см.
)
рассчитывают при помощи уравнений метода сил (см.
)
,в которых коэффициенты при неизвестных (перемещения) определяют с учётом действия только нормальных усилий в элементах Ф. При расчёте Ф. на
используют т. н. линии влияния.
Лит.см. при статьях
,
,
,
.
Л. В. Касабьян.
Классификация ферм по типам решётки: а — балочная раскосная; б — балочная с треугольной решёткой; в — балочно-консольная с треугольной решёткой и дополнительными стойками; г — консольная полураскосная; д — консольная двухраскосная; е — балочная двухрешётчатая; 1 — верхний пояс; 2 — нижний пояс; 3 — раскос; 4 — стойка.
Фермана
Фермана'(Fermanagh), административный округ в Северной Ирландии (Великобритания), в бассейне озёр Лох-Эрн и Аппер-Лох-Эрн. Площадь 1,7 тыс.
км
3
.Население 50,3 тыс. чел. (1971). Главный город – Эннискиллен. Сельскохозяйственный район (мясо-молочное животноводство).
Фермата
Ферма'та(итал. fermata, буквально – остановка) (музыкальная), знак ( или ) в нотном письме, обозначающий продление ноты или паузы, над или под которой он стоит, на неопределённое время (обычно в 1
1/
2—2 раза). Продолжительность звука или паузы с Ф. исполнитель определяет по собственному усмотрению. Ф. над тактовой чертой обозначает неопределенной продолжительности паузу.
Ферментативные методы анализа
Ферментати'вные ме'тоды ана'лиза, методы количественного определения химических веществ в растворе, основанные на использовании
.С помощью Ф. м. а. определяют вещества, способные участвовать в химических реакциях, катализируемых ферментами, а также являющиеся активаторами либо ингибиторами ферментов. Ф. м. а. характеризуются высокой чувствительностью и специфичностью, поскольку ферменты катализируют превращения веществ с большой скоростью и высоко избирательно, даже если анализируемое соединение находится в смеси с др. близкими по химическому строению веществами.
При определении субстрата ферментативной реакции к анализируемой пробе прибавляют фермент и др. необходимые для реакции компоненты. По окончании реакции тем или иным удобным методом устанавливают в растворе содержание продукта реакции. Например, определение этилового спирта в растворе с помощью фермента алкогольдегидрогеназы (АДГ) производится при участии кофермента АДГ –
(НАД). Последний в ходе ферментативной реакции количественно превращается в восстановленный НАД, обладающий, в отличие от окисленной формы, способностью к поглощению ультрафиолетового света при длине волны 340
нм.Измеряя это поглощение, можно установить концентрацию восстановленного НАД и рассчитать концентрацию этилового спирта. Метод позволяет определить 1
мкгспирта в 1
млраствора. Многие Ф. м. а. основаны на определении изменения кислотности раствора в ходе ферментативной реакции. Например, эфиры карбоновых, фосфорной и др. кислот можно определять с помощью специфических ферментов, катализирующих их гидролиз. Поскольку при гидролизе образуются соответствующие кислоты, результат их титрования по окончании реакции позволяет рассчитать концентрацию определяемого эфира.
При Ф. м. а. часто используют комбинацию (сопряжение) нескольких ферментативных реакций. Например, концентрация глюкозы может быть определена с помощью ферментов глюкозооксидазы (ГО) и пероксидазы (ПО). Под действием ГО глюкоза превращается в глюконовую кислоту, при этом образуется перекись водорода, которая, в свою очередь, под влиянием ПО может окислить введённый в раствор ортодианизидин (или толидин) и давать окраску. Измеряя интенсивность окраски раствора, можно рассчитать исходную концентрацию глюкозы (чувствительность метода 5
мкгв пробе). Этот способ применяется для быстрого определения глюкозы в моче у больных диабетом с помощью индикаторной бумажки, пропитанной указанными реактивами.
Разновидностью Ф. м. а. являются кинетические методы анализа, основанные на зависимости скорости ферментативной реакции от концентрации анализируемых веществ (см.
)
,которыми могут быть субстраты, активаторы или ингибиторы ферментов. Зная характер этой зависимости, можно, измеряя скорость ферментативной реакции, рассчитать концентрацию анализируемого вещества. Например, количественное определение фосфорорганических инсектицидов, являющихся сильными ингибиторами, фермента
производится путём измерения активности этого фермента в отсутствии и в присутствии ингибитора. Чувствительность метода определения, например диэтил-
-нитрофенилфосфата, составляет 0,015
мкгв пробе, ионов магния (по активирующему их влиянию на фермент, окисляющий изолимонную кислоту) – 0,1
мкг.
Широкое распространение получили Ф. м. а., основанные на использовании ферментов, прочно связанных с твёрдыми носителями, которыми могут быть полимеры, неорганические сорбенты, гели. Такие «твёрдые ферменты», помещенные на электрохимические датчики (стеклянные, платиновые и др. электроды), представляют собой ферментные электроды, служащие инструментами для измерения скорости ферментной реакции в растворе анализируемого вещества. С помощью ферментных электродов определяют мочевину, аминокислоты, пенициллин, глюкозу и т.д. с чувствительностью 0,1–0,01
мкгв пробе.
Лит.:Березин И. В., Клесов А. А., Ферментные электроды, «Успехи химии», 1976, т. 45, в. 2: Methoden der enzymatische Analyse, Hrsg. Н. U. Bergmeyer, 3 Aufl., Bd 1–2, Weinheim, 1974.
В. А. Яковлев.
Ферментативный катализ
Ферментати'вный ката'лиз,биокатализ, ускорение химических реакций под влиянием
.В основе жизнедеятельности лежат многочисленные химические реакции расщепления питательных веществ, синтеза необходимых организму химических соединений и трансформации их энергии в энергию физиологических процессов (работа мышц, почек, нервная деятельность и т.п.). Все эти реакции не могли бы происходить с необходимой для живых организмов скоростью, если бы в ходе эволюции не возникли механизмы их ускорения с помощью Ф. к.
Одно время считалось, что Ф. к. принципиально отличается от небиологического
,широко используемого в химическом производстве. Такое представление основывалось на трёх отличительных особенностях Ф. к.: исключительно высокой эффективности (увеличение скорости реакции в 10
10–10
13раз) и специфичности, т. е. избирательности (способности каждого фермента катализировать превращение строго определённых биологических субстратов, иногда лишь единственного вещества, в единственном направлении), не достижимых в небиологическом катализе. Особенностью Ф. к. является также его регулируемость – способность биокатализатора – фермента – увеличивать или уменьшать свою активность в зависимости от потребностей организма. Однако исследование механизма Ф. к. показывает, что к нему применимы законы и принципы, на которых основаны обычные химические реакции. Отличие реакций Ф. к. определяется сложностью структуры ферментов и химических превращений, которые совершают вещества в ходе катализа.
Эффективность Ф. к. достигается в результате того, что химическая реакция разбивается на ряд энергетически более лёгких промежуточных реакций, в которых участвует фермент. Важнейшая для Ф. к. реакция – образование первичного фермент-субстратного комплекса даёт выигрыш энергии, достаточный для ускорения процесса в целом. Представления о необходимости образования такого комплекса следовали из изучения зависимости скорости ферментативной реакции (V) от концентрации фермента (
Е) и субстрата (S), которая описывается уравнением Михаэлиса – Ментен:
Страницы:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30
|
|

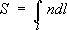
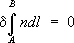 (см.
), где
Аи
В –точки, между которыми распространяется свет. Это выражение и представляет собой математическую формулировку Ф. п.
(см.
), где
Аи
В –точки, между которыми распространяется свет. Это выражение и представляет собой математическую формулировку Ф. п.