 |
|
Популярные авторы:: Борхес Хорхе Луис :: Азимов Айзек :: Раззаков Федор :: Грин Александр :: Толстой Лев Николаевич :: Горький Максим :: Сименон Жорж :: Чехов Антон Павлович :: Картленд Барбара :: Андреев Леонид Николаевич Популярные книги:: Дюна (Книги 1-3) :: The Boarding House :: Бессмертие человеческой личности как научная проблема :: Опасная любовь :: Последний путь Владимира Мономаха :: Конец материи :: Странник в раю :: Улики :: Наш бедный индивидуализм :: Кот, который гулял под землей |
Большая Советская Энциклопедия (ДВ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ДВ) - Чтение (стр. 8)
Например, в СССР областное управление сельского хозяйства работает непосредственно под руководством исполкома областного Совета депутатов трудящихся и министерства сельского хозяйства соответствующей союзной республики. Двойное подчинение, писал В. И. Ленин, необходимо там, где надо учитывать действительно существующие неизбежные различия. «Земледелие в Калужской губернии не то, что в Казанской. То же относится ко всей промышленности. То же относится ко всему администрированию или управлению» (Полн.собр. соч., 5 изд., т. 45, с. 198).
Д. п. применяется на различных уровнях управления. Ст. 101 Конституции СССР устанавливает, что исполнительные органы Советов депутатов трудящихся непосредственно подотчётны как избравшему их Совету депутатов трудящихся, так и исполнительному органу вышестоящего Совета депутатов трудящихся. Согласно ст. 52 Конституции РСФСР, союзно-республиканские министерства РСФСР руководят порученными им отраслями государственного управления РСФСР, подчиняясь как Совету Министров РСФСР, так и соответствующим союзно-республиканским министерствам СССР. Аналогичные статьи содержатся и в конституциях др. союзных республик. В силу Д. п. вышестоящие органы по отношению к нижестоящим имеют право: направлять и контролировать их деятельность; избирать или назначать руководящий состав этих органов; отменять, приостанавливать и изменять правовые акты, принятые этими органами. Юридически Д. п. закрепляется обычно в положении об органе управления, находящемся в Д.п. В. Г. Вишняков. Двойной ряд Двойной ряд,выражение вида u 11 + u 12 + ... + u 1n + ... + u 21+ u 22+ ... + u 2n+ ... .................................... + u m1 + u m2+ ... + u mn + ... ....................................., составленное из элементов бесконечной матрицы|| u mn|| ( m, n= 1, 2, ...); эти элементы могут быть числами (тогда Д. р. называются числовым), функциями от одного или нескольких переменных (функциональный Д. р.) и т. д. Для Д. р. принята сокращённая запись
u mnназывается общим членом Д. р. Конечные суммы
называются частичными суммами Д. р. Если существует предел
когда mи nнезависимо друг от друга стремятся к бесконечности, то этот предел называется суммой Д. р. и Д. р. называются сходящимся. Теория сходимости Д. р. значительно сложнее соответствующей теории для простых ;например, в отличие от простых рядов, из сходимости Д. р. не вытекает, что его частичные суммы ограничены. Выражение
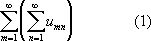
называется повторным рядом. Его надо понимать в том смысле, что сначала вычисляются суммы
всех внутренних рядов, а затем рассматривается ряд
составленный из этих сумм. Если повторный ряд (1) сходится и имеет сумму S,то её называют суммой Д. р. по строкам. Аналогично определяется сумма S'Д. р. по столбцам. Из сходимости Д. р. не вытекает, что сходятся внутренние Ряды
так что суммы по строкам и по столбцам могут и не существовать. Напротив, если Д. р. расходится, то может оказаться, что существуют суммы по строкам и по столбцам и S¹ S'.Однако, если Д. р. сходится и имеет сумму Sи существуют суммы по строкам и по столбцам, то каждая из этих сумм равна S. Это обстоятельство постоянно используется при фактическом вычислении суммы Д. р. Наиболее важными классами Д. р. являются двойные степенные ряды, двойные ряды Фурье и квадратичные формы с бесконечным числом переменных. Для Д. р. Фурье
одним из стандартных пониманий суммы таких рядов является следующее: образуются круговые (или сферические) частичные суммы
где суммирование распространяется на всевозможные пары целых чисел (
m, n)
,для которых
m
2+ n
2<
N,и рассматривается предел
Кратный ряд (точнее, s-кpaтный ряд) есть выражение вида S m, n, …, pu mn … q, составленное из членов таблицы || u mn...p||. Каждый член этой таблицы занумерован sиндексами m, n, ..., р,и эти индексы пробегают независимо друг от друга все натуральные числа. Теория кратных рядов совершенно аналогична теории Д. р. Лит.:Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 6 изд., т. 2, М., 1966. С. Б. Стечкин. Двойной суперфосфат Двойно'й суперфосфа'т, концентрированное фосфорное удобрение; см. . Двойной электрический слой Двойно'й электри'ческий сло'й,два весьма близких друг к другу слоя электрических зарядов разного знака, но с одинаковой поверхностной плотностью, возникающие на границе раздела двух фаз. Д. э. с. в целом электронейтрален. При пересечении Д. э. с. электрический потенциал изменяется скачком. Д. э. с. на поверхности металла возникает из-за того, что электроны металла несколько выходят за пределы решётки, образованной положительными ионами. Скачок потенциала в таком Д. э. с. является составной частью электрона из металла. Для электрохимии большое значение имеет Д. э. с. на границе раздела металл - электролит. При погружении металла в раствор, содержащий ионы этого металла, образуется специфический для границы электрод - раствор ионный Д. э. с. дополнительно к Д.э.с., существовавшему на поверхности металла до погружения, и Д. э. с., возникающему в результате ориентации полярных молекул растворителя (например, воды) у поверхности металла. Так, при погружении серебряной пластинки в раствор KNO 3, содержащий очень мало AgNO 3, ионы Ag+ переходят из металла в раствор, избыточные электроны в металле заряжают его поверхность отрицательно и притягивают из раствора ионы К +, образующие у поверхности вторую (положительную) обкладку Д. э. с. (см. рис. ). Возникающий скачок потенциала приостанавливает дальнейший переход ионов Ag+, и наступает равновесие электрода с раствором. Если концентрация AgNO 3в растворе велика, то, наоборот, ионы Ag+ из раствора переходят в металл, его поверхность заряжается положительно и притягивает из раствора ионы NO 3Существует промежуточная концентрация ионов металла, при которой поверхность металла не заряжается; соответствующий потенциал электрода называется потенциалом нулевого заряда, или нулевой точкой. Важное понятие о нулевой точке как величине, характерной для данного электрода, введено в электрохимию советским учёным А. Н. Фрумкиным. На ноны в Д. э. с. действуют одновременно электростатические силы и силы теплового движения. В результате взаимно противоположного влияния этих сил лишь часть ионов остаётся непосредственно вблизи поверхности электрода (плотная часть Д. э. с., или слой Гельмгольца), а остальные распределяются диффузно в растворе на некотором расстоянии от электрода (диффузный Д. э. с., или слой Гуи). Степень диффузности увеличивается с ростом температуры, а также при уменьшении концентрации раствора электролита и при уменьшении заряда электрода. Средняя толщина плотной части Д. э. с. порядка радиуса иона (несколько А), поэтому Д. э. с. обладает высокой электрической ёмкостью (~10 -5 ф/см 2) и внутри него действует сильное электрическое поле (~10 6 в/см) . Строение Д. э. с. оказывает большое влияние на электрические свойства межфазных границ и на протекающие на них процессы - прежде всего, на механизм и кинетику электрохимических реакций, на электрокинетические явления, на устойчивость коллоидных систем и т. п. Для исследования Д. э. с. используются методы измерения поверхностного натяжения и ёмкости, адсорбционные измерения и др. Лит.:Фрумкин А. Н., Багоцкий В.С., Иофа З. А., Кабанов Б. Н., Кинетика электродных процессов, М., 1952; Парсонс Р., Равновесные свойства заряженных межфазных границ, в кн.: Некоторые проблемы современной электрохимии, пер. с англ., М., 1958; Делахе и П., Двойной слой и кинетика электродных процессов, пер. с англ., М., 1967. Ю. В. Плесков. 
Рис. к ст. Двойной электрический слой. Двойные звёзды Двойны'е звёзды,две звезды, близкие друг другу в пространстве и составляющие физическую систему, компоненты которой связаны силами взаимного тяготения. Компоненты обращаются по эллиптическим орбитам вокруг общего центра масс и вместе движутся в Галактике. Д. з. являются частным случаем , состоящих иногда из нескольких Компонентов (до 8). По методике обнаружения различают: визуально-двойные звёзды (их компоненты можно увидеть при помощи телескопа визуально или сфотографировать); спектрально-двойные звёзды (двойственность проявляется в периодических смещениях или раздвоениях линий их спектров); затменно-двойные звёзды (их компоненты периодически загораживают друг друга от наблюдателя); астрометрические Д. з., или тёмные спутники (очень точные измерения положений позволяют обнаружить периодические смещения звезды под влиянием обращающегося вокруг неё тёмного спутника); фотометрические Д. з. (при различии в температуре поверхностей компонентов точная многоцветная электрофотометрия показывает её отличие от одиночных звёзд). Иногда о двойственности какой-нибудь звезды можно судить по её сложному (комбинированному) спектру либо по одинаковому заметному собственному движению двух не слишком близко расположенных звёзд (широкие пары). Кратные системы могут состоять из Д. з. разного вида. Так, компонент визуально-двойной звезды сам может оказаться двойной одного из перечисленных видов. Описанные типы Д. з., представляющих собой физические системы, называются физическими Д. з. Вид Д. з. имеют также пары звёзд, компоненты которых разделены громадными расстояниями по лучу зрения и лишь случайно (и временно) располагаются в непосредственной видимой близости друг к другу на небесной сфере. С течением времени они разойдутся и перестанут считаться Д. з. Такие системы называются оптическими Д. з. При составлении каталогов к числу Д. з. относят лишь те объекты, у которых расстояния между компонентами не превышают некоторого предела, зависящего от блеска (видимой звёздной величины) главной звезды и её спутника. Так, две звезды 2-й звёздной величины могут считаться компонентами Д. з., если расстояние между ними меньше 40’’, две звезды 9-й звёздной величины - не более 3’’ и т. д. Всестороннее изучение Д. з. имеет большое значение, т. к. оно даёт способ надёжного определения масс звёзд, а в ряде случаев - определения размеров компонентов и их формы, плотности и закона её изменения с расстоянием от центра звезды, а также строения звёздных атмосфер. Все др. способы определения масс звёзд опираются на определения масс Д. з. Изучение Д. з. началось в середине 17 в., когда Г. Галилей открыл несколько Д. з. и предложил метод определения относительного яркой главной звезды оптической Д. з. по отношению к более слабой и поэтому, вероятно, более далёкой. К середине 18 в. было обнаружено всего около 20 Д. з.; тогда же начались и первые измерения позиционного угла спутника q и расстояния между компонентами r ( рис. 1 ). После 25 лет наблюдений английский астроном В. Гершель в 80-х гг. 18 в. обнаружил у некоторых Д. з. явное орбитальное (т. к. оно было криволинейным) движение спутника относительно главной звезды и оценил периоды обращения нескольких из них. Так были открыты физические Д. з. Русский астроном В. Я. Струве заложил твёрдый фундамент учения о Д. з. своими многолетними исследованиями. Он открыл много новых Д. з. (его каталог 3110 Д. з. опубликован в 1827), измерил положение спутников у 2640 Д. з. (опубликовано в 1837), на меридианном круге определял точные положения Д. з. в течение 20 лет (опубликовано в 1852). Английский астроном Дж. Гершель распространил исследования Д. з. на Южное полушарие неба. Русский астроном О. В. Струве исследовал проблему систематических ошибок при измерении Д. з. К середине 20 в. известно около 60 000 визуально-двойных звёзд. Для измерения визуально-двойных звёзд со времён В. Гершеля применяются разных видов, а для самых малых угловых расстояний - . На больших телескопах можно измерять расстояния до 0,1-0,2’’. Применение фотографии к измерениям Д. з. даёт прекрасные результаты для расстояний больше 1-2’’. Видимое относительное движение спутника вокруг главной звезды совершается по эллипсу (включая окружность и прямую как частные виды этой кривой). Главная звезда всегда находится внутри эллипса, но обычно не в фокусе видимой орбиты. Радиус-вектор (соединяющий главную звезду со спутником) описывает площади, пропорциональные времени, т. е. для Д. з. соблюдается 2-й . Видимая орбита Д. з. ( рис. 2 , а) является проекцией истинной орбиты ( рис. 2 , б) на картинную плоскость (перпендикулярную лучу зрения). Разработано много методов определения элементов орбит Д. з.: большой полуоси, наклона орбиты, эксцентриситета, позиционного угла линии узлов, по которой плоскость орбиты пересекает картинную плоскость, долготы периастра (угла между линией узлов и линией, соединяющей периастр с апоастром в плоскости истинной орбиты), периода обращения и момента (даты) прохождения спутника через периастр. Из нескольких десятков тысяч визуально-двойных звёзд только около 2000 обнаруживают орбитальное движение и лишь для примерно 300 вычислены орбиты. Самый короткий период (1,72 года) имеет звезда BD -8°4352; из больших периодов более или менее достоверны лишь те, которые не превышают 500 лет. Для пар с одинаковым большим собственным движением периоды формально получаются порядка сотен тысяч лет. Первая спектрально-двойная звезда была открыта в 1889. В её спектре происходит периодическое раздвоение спектральных ( рис. 2 ) линий, что свидетельствует об орбитальном движении обоих компонентов вокруг общего центра масс. У других Д. з. этого типа наблюдаются периодические смещения одиночных линий: линии более слабого компонента в спектре не заметны. Анализ кривой изменения лучевых скоростей спектрально-двойной звезды позволяет найти следующие элементы орбиты: период, эксцентриситет, момент (дату) прохождения периастра, долготу периастра, а также произведение asin i( а -большая полуось, I -наклон орбиты) и лучевую скорость g центра масс. Некоторое представление о характере лучевых скоростей в зависимости от формы и расположения орбиты даёт рис. 3 . Из примерно 2000 открытых спектрально-двойных звёзд орбиты вычислены для 500. Их периоды составляют от 4,7 часа до 60 лет. Если наклон орбиты близок к 90°, можно наблюдать периодические взаимные затмения компонентов. В зависимости от относительных размеров и яркостей компонентов общий блеск затменно-двойной звезды будет испытывать более или менее продолжительные и глубокие минимумы. По форме кривой блеска такой звезды ( рис. 4 ) можно судить об элементах её орбиты. Самый короткий из известных периодов 4,7 часа, самый длинный - 57 лет. В 1911 русский астроном С. Н. Блажко разработал первый общий метод вычисления орбит затменно-двойных звёзд. Анализ кривых изменения блеска позволяет определить не только элементы орбиты затменно-двойной звезды, но и относительные размеры звёзд по сравнению с размерами орбиты, форму звёзд и их поверхностную яркость. В сочетании с результатами др. наблюдений Д. з. такой анализ даёт возможность определить многие звёздные характеристики. Так, если получена также кривая лучевых скоростей, то можно определить размеры орбиты и диаметры самих звёзд в км,а также и светимости звёзд. В некоторых (правда, редких) случаях можно изучать также строение и состав звёздных атмосфер, наличие расширяющихся и вращающихся оболочек, закон потери массы более массивной звездой и эволюцию системы. Применение 3-го закона Кеплера к Д.з., для которых известно расстояние, позволяет вычислить сумму масс компонентов, выраженную в единицах массы Солнца:
где p - параллакс звезды, а -большая полуось орбиты в секундах дуги, Р -период обращения. Если из наблюдений можно определить также отношение масс компонентов, тогда можно вычислить массу каждого компонента отдельно. Для спектрально-двойных звёзд можно определить лишь величину ( 1+ 2) sin 3 i. Если в спектре видны линии обоих компонентов, можно определить также отношение масс. Совокупность всех определений масс компонентов Д. з. позволила обнаружить важную для астрономии зависимость между массами и светимостями звёзд (см. ) ;она получила теоретическое обоснование и теперь широко используется для определения масс одиночных звёзд по их светимостям. Специальные (очень трудоёмкие и тонкие) исследования собственных движений некоторых звёзд показали наличие вокруг них одного или нескольких планетоподобных тел с массами порядка массы планеты Юпитер. Это дало первые надёжные доказательства существования др. планетных систем, кроме солнечной. Двойственность (и вообще кратность) - весьма распространённое явление среди звёзд Галактики. Весьма вероятно, что кратных систем больше, чем одиночных звёзд. По крайней мере, в галактических окрестностях Солнца (где, можно полагать, почти все звёзды нам известны) из 30 звёзд 17 одиночных и 13 кратных (29 компонентов). По своим физическим характеристикам и кинематике Д. з. не отличаются от одиночных звёзд и, по-видимому, имеют одинаковое с ними происхождение. Предложено несколько различных гипотез происхождения Д. з.: деление одиночных звёзд при нарушении устойчивости в результате быстрого осевого вращения; захват одной звезды другой; совместное образование в недрах одной туманности. Весьма вероятно, что кратные звёзды образуются в Теория происхождения Д. з. должна также объяснить ряд замеченных статистических закономерностей в соотношениях между различными физическими характеристиками Д. з. и элементами их орбит. Специальный интерес представляют собой двойные, в состав которых входят переменные звёзды. Д. з., как и ,являются подходящими объектами для проверки современных представлений об эволюции звёзд. Лит.:Мартынов Д. Я., Курс общей астрофизики, М., 1965, гл. 3; Курс астрофизики и звёздной астрономии, под ред. А. А. Михайлова, т. 2, М., 1962, гл. 3-5; Струве О. и 3ебергс В., Астрономия 20 века, пер. с англ., М., 1968, гл. 14; Методы астрономии, под ред. В. Хилтнера, пер. с англ., М., 1967, гл. 22-24; Aitken R. G., Binary stars, 2ed., N.Y. - L., 1935. П. Г. Куликовский. 
Рис. 3. Зависимость лучевых скоростей от формы и расположения орбиты спектрально-двойной звезды: е - эксцентриситет орбиты; w - долгота периастра. 
Рис. 1 к ст. Двойные звёзды. 
Рис. 2 к ст. Двойные звёзды. 
Рис. 4. Кривая блеска затменно-двойной звезды и соответствующая ей система двух звёзд. Двойные системы Двойны'е систе'мы,бинарные системы, двухкомпонентные системы, физико-химические системы, состоящие из двух независимых составных частей (компонентов). Особое практическое значение имеют конденсированные Д. с., т. е. не содержащие газов или паров. и таких систем изображают на плоскости, откладывая на оси абсцисс состав х(выраженный в процентах по массе, атомных или мольных процентах одного из компонентов), а на оси ординат - температуры Тфазовых превращений (начала и конца кристаллизации, полиморфных превращений и др.) или численные значения измеримых свойств Д. с. (плотности, твёрдости, электропроводности и др.). Здесь рассмотрены лишь простейшие изобарические (при давлении 1 атм) диаграммы состояния Д. с., в которых существуют только жидкие фазы Lи твёрдые S. О Д. с., состоящих только из жидких фаз или из жидкостей и газа (пара), см. ; оД. с. из твёрдых фаз и газа (пара) см. . Если взаимная растворимость компонентов Аи Вв жидком и в твёрдом состоянии отсутствует, то диаграмма состояния ( рис. 1 ) изображается двумя горизонтальными прямыми, проведёнными через точки Т Аи T B,отвечающие температурам плавления Аи В.Выше T Bсистема состоит из двух жидких фаз L Aи L B,между T Bи T A-из L Aи кристаллов В,ниже T A-из смеси кристаллов Аи В.Если взаимная растворимость компонентов Аи Вв жидком состоянии не ограничена, а в твёрдом состоянии отсутствует, то из одной жидкой фазы Lпри охлаждении выпадают две твёрдые фазы - кристаллы Аи В( рис. 2 ). Кривые ликвидуса (геометрия, место температур начала кристаллизации) T AEи T BEпересекаются в эвтектической точке Е(см. ) .Жидкость, состав которой отвечает точке Е,затвердевает при постоянной температуре в тонкую смесь кристаллов Аи В.Из жидкостей, состав которых лежит между Аи Е,при охлаждении начинают выпадать кристаллы А,вследствие чего содержание Вв жидкости увеличивается; когда её состав будет отвечать точке Е,процесс закончится кристаллизацией эвтектики. Точно так же затвердевание жидкостей, состав которых лежит между Ви Е,начинается выпадением кристаллов Ви заканчивается кристаллизацией эвтектики. Прямая FG,проведённая через точку Е,называется линией солидуса (геометрическое место температур конца кристаллизации). Затвердевшие Д. с. этого типа состоят из двухфазной смеси кристаллов А+В.Изотермы свойств таких смесей приближаются к прямой линии e Аe В( рис. 2 ). Если компоненты Аи Вобладают неограниченной взаимной растворимостью как в жидком, так и в твёрдом состоянии, то из одной жидкой фазы Lпри охлаждении выпадает только одна кристаллическая фаза - S ( рис. 3 ). Диаграмма состояния такой Д. с. может быть без максимума и минимума ( рис. 3, I ), с максимумом ( рис. 3, II ) и с минимумом ( рис. 3, III ) .Изотермы свойств имеют вид непрерывных кривых, обращенных выпуклостью вверх ( рис. 3, IV ) или вниз ( рис. 3, V ). Если взаимная растворимость Аи Вв жидком состоянии не ограничена, а в твёрдом - ограничена, то в случае образования эвтектики последняя состоит из смеси двух твёрдых растворов ( и b ( рис. 4 ), предельные концентрации которых отвечают точкам Fи G при эвтектической температуре и точкам Ми Nпри комнатной. Изотермы состав - свойство (отвечающие температуре t) состоят из 3 ветвей e Am 1n 1e Bи eAm 2n 2e B ,точки m 1, m 2и n 1, n 2отвечают предельным концентрациям твёрдых растворов a и b при температуре t. В случае, когда из жидкости Lкристаллизуется одно химическое соединение С, плавящееся без разложения, и твёрдые растворы отсутствуют, на кривой ликвидуса наблюдается либо рациональный максимум М,либо сингулярная точка D,отвечающие составу соединения С, и две эвтектические точки E 1и E 2, отвечающие эвтектикам, образуемым С с А и Всоответственно ( рис. 5 ). Изотермы свойств имеют вид двух прямых, пересекающихся на ординате соединения С. Более сложные случаи диаграмм состояния Д. с. см. в приведённой ниже литературе. Лит.:Курнаков Н. С., Избр. труды, т. 1-3, М., 1960-63; Вол А. Е., Строение и свойства двойных металлических систем, т. 1-2, М., 1959-62; Хансен М., Андерко К., Структуры двойных сплавов, пер. с англ. , М. , 1962; см. также лит. при ст. . С. А. Погодин. 
Рис. 1 к ст. Двойные системы. 
Рис. 3 к ст. Двойные системы. 
Рис. 5 к ст. Двойные системы. 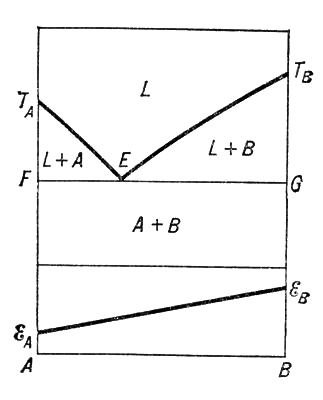
Рис. 2 к ст. Двойные системы. 
Рис. 4 к ст. Двойные системы. Двойственная истина Дво'йственная и'стина,двойная истина, термин, обозначающий учение о разделении философских и богословских истин, согласно которому истинное в философии может быть ложным в теологии и наоборот. Учение о Д. и. возникло в средние века, в эпоху распространения философии Аристотеля, когда обнаружилось, что ряд философских положений аристотелевской системы противоречит догматам ислама и христианства. Наиболее влиятельным мыслителем, опиравшимся на учение о Д. и. в своей полемике с мусульманскими богословами, был .Из этого же учения исходили и французский 13 в. (его главой в Парижском университете был Сигер Брабантский), представители английского ( ,У. ) .Широкое распространение учение о Д. и. получило в эпоху Возрождения (Помпонацци, падуанская школа аверроистов и др.). Учение о Д. и. способствовало развитию рационализма. Двойственности принцип Дво'йственности при'нцип,принцип, формулируемый в некоторых разделах математики и заключающийся в том, что каждому верному утверждению этого раздела отвечает двойственное утверждение, которое может быть получено из первого путём замены входящих в него понятий на другие, т. н. двойственные им понятия. 1) Д. п. формулируется в проективной геометрии на плоскости. При этом двойственными понятиями являются, например, «точка» и «прямая», «точка лежит на прямой» и «прямая проходит через точку». Каждой аксиоме в проективной геометрии на плоскости формулируется двойственное предложение, которое может быть доказано с помощью этих же аксиом (этим обосновывается Д. п. в проективной геометрии на плоскости). Двойственными утверждениями в проективной геометрии на плоскости являются известные теоремы Паскаля и Брианшона. Первая из этих теорем утверждает, что во всяком шестивершиннике, вписанном в линию 2-го порядка, точки пересечения противоположных сторон лежат на одной прямой ( рис. 1 ). Вторая теорема утверждает, что во всяком шестистороннике, описанном около линии 2-го порядка, прямые, соединяющие противоположные вершины, пересекаются в одной точке ( рис. 2 ). 2) Д. п. в абстрактной теории множеств. Пусть дано множество М.Рассмотрим систему всех его подмножеств А, В, Си т.д. Справедливо следующее предложение: если верна теорема о подмножествах множества М,которая формулируется лишь в терминах операций суммы, пересечения и дополнения, то верна также и теорема, получающаяся на данной путём замены операции суммы и пересечения соответственно операциями пересечения и суммы, пустого множества L - всем множеством М,а множества М -пустым множеством L. При этом дополнение суммы заменяется пересечением дополнений, а дополнение пересечения - суммой дополнений. Пример 1. Верному соотношению ( A И В) З С =( A З С) И( ВЗ С) двойственно соотношение (также верное) ( АЗ B) И C =( A И С) З( В И С) Пример 2. Верному соотношению (AИB)И(З`B) = M двойственно соотношение (также верное) (З `B)З(АИ В) = L , где ,`B -дополнения множеств А, В во множестве М, А З В -сумма множеств А и В, A З В- их пересечение. 3) Д. п. имеет место в математической логике (в исчислении высказываний и в исчислении предикатов). 4) О топологических законах двойственности см. .
Лит.:Ефимов Н. В., Высшая геометрия, 4 изд., М., 1961; Александров П. С., Введение в общую теорию множеств и функций, М. - Л., 1948; Гильберт Д. и Аккерман В., Основы теоретической логики, пер. с нем., М., 1947. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 |
|||||||
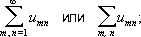

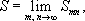
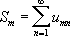
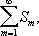
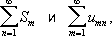
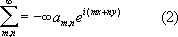

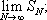 этот предел называется сферической суммой Д. р. Фурье (2). Многие важные функции изображаются с помощью Д. р., например
Вейерштрасса.
этот предел называется сферической суммой Д. р. Фурье (2). Многие важные функции изображаются с помощью Д. р., например
Вейерштрасса.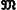 1+
2=
a
3/p
3P
2,
1+
2=
a
3/p
3P
2,