Большая Советская Энциклопедия (ЧИ)

Число',важнейшее математическое понятие. Возникнув в простейшем виде ещё в первобытном обществе, понятие Ч. изменялось на протяжении веков, постепенно обогащаясь содержанием по мере расширения сферы человеческой деятельности и связанного с ним расширения круга вопросов, требовавшего количеств. описания и исследования. На первых ступенях развития понятие Ч. определялось потребностями счёта и измерения, возникавшими в непосредственной практической деятельности человека. Затем Ч. становится основным понятием математики, и дальнейшее развитие понятия Ч. определяется потребностями этой науки.

  Понятие натурального числа, вызванное потребностью счёта предметов, возникло ещё в доисторические времена. Процесс формирования понятия натурального Ч. протекал в общих чертах следующим образом. На низшей ступени первобытного общества понятие отвлечённого Ч. отсутствовало. Это не значит, что первобытный человек не мог отдавать себе отчёта о количестве предметов конкретно данной совокупности, например о количестве людей, участвующих в охоте, о количестве озёр, в которых можно ловить рыбу, и т.д. Но в сознании первобытного человека ещё не сформировалось то общее, что есть в объектах такого рода, как, например, «три человека», «три озера» и т.д. Анализ языков первобытных народностей показывает, что для счёта предметов различного рода употреблялись различные словесные обороты. Слово «три» в контекстах «три человека», «три лодки» передавалось различно. Конечно, такие именованные числовые ряды были очень короткими и завершались неиндивидуализированным понятием («много») о большом количестве тех или других предметов, которое тоже являлось именованным, т. е. выражалось разными словами для предметов разного рода, такими, как «толпа», «стадо», «куча» и т.д.

  Источником возникновения понятия отвлечённого Ч. является примитивный счёт предметов, заключающийся в сопоставлении предметов данной конкретной совокупности с предметами некоторой определённой совокупности, играющей как бы роль эталона. У большинства народов первым таким эталоном являются пальцы («счёт на пальцах»), что с несомненностью подтверждается языковедческим анализом названий первых чисел. На этой ступени Ч. становится отвлечённым, не зависящим от качества считаемых объектов, но вместе с тем выступающим во вполне конкретном осуществлении, связанном с природой эталонной совокупности. Расширяющиеся потребности счёта заставили людей употреблять другие счётные эталоны, такие, как, например, зарубки на палочке. Для фиксации сравнительно больших Ч. стала использоваться новая идея - обозначение некоторого определённого Ч. (у большинства народов - десяти) новым знаком, например зарубкой на другой палочке.

  С развитием письменности возможности воспроизведения Ч. значительно расширились. Сначала Ч. стали обозначаться чёрточками на материале, служащем для записи (папирус, глиняные таблички и т.д.). Затем были введены другие знаки для больших Ч. Вавилонские клинописные обозначения Ч., так же, как и сохранившиеся до наших дней «римские цифры», ясно свидетельствуют именно об этом пути формирования обозначений для Ч. Шагом вперёд была индийская позиционная система , позволяющая записать любое натуральное Ч. при помощи десяти знаков - .Т. о., параллельно с развитием письменности понятие натурального Ч. принимает всё более отвлечённую форму, всё более закрепляется отвлечённое от всякой конкретности понятие Ч., воспроизводимого в форме слов в устной речи и в форме обозначения специальными знаками в письменной.

  Важным шагом в развитии понятия натурального Ч. является осознание бесконечности натурального ряда Ч., т. е. потенциальной возможности его безграничного продолжения. Отчётливое представление о бесконечности натурального ряда отражено в памятниках античной математики (3 в. до н. э.), в трудах Евклида и Архимеда. В «Началах» Евклида устанавливается даже безграничная продолжаемость ряда простых Ч., в книге Архимеда «Псаммит» - принципы для построения названий и обозначений для сколь угодно больших Ч., в частности бо'льших, чем «число песчинок в мире».

  С развитием понятия натурального Ч. как результата счёта предметов в обиход включаются действия над Ч. Действия сложения и вычитания возникают сначала как действия над самими совокупностями в форме объединения двух совокупностей в одну и отделения части совокупности. Умножение, по-видимому, возникло в результате счёта равными частями (по два, по три и т.д.), деление - как деление совокупности на равные части (см. , ) .Лишь в многовековом опыте сложилось представление об отвлечённом характере этих действий, о независимости количественного результата действия от природы предметов, составляющих совокупности, о том, что, например, два предмета и три предмета составят пять предметов независимо от природы этих предметов. Тогда стали разрабатывать правила действий, изучать их свойства, создавать методы для решения задач, т. е. начинается развитие науки о Ч. - .В первую очередь арифметика развивается как система знаний, имеющая непосредственно прикладную направленность. Но в самом процессе развития арифметики проявляется потребность в изучении свойств Ч. как таковых, в уяснении всё более сложных закономерностей в их взаимосвязях, обусловленных наличием действий. Начинается детализация понятия натурального Ч., выделяются классы чётных и нечётных Ч., простых и составных и т.д. Изучение глубоких закономерностей в натуральном ряду Ч. продолжается и составляет раздел математики, носящий название .

 Натуральные Ч., кроме основной функции - характеристики количества предметов, несут ещё другую функцию - характеристику порядка предметов, расположенных в ряд. Возникающее в связи с этой функцией понятие порядкового Ч. (первый, второй и т.д.) тесно переплетается с понятием количественного Ч. (один, два и т.д.). В частности, расположение в ряд считаемых предметов и последующий их пересчёт с применением порядковых Ч. является наиболее употребительным с незапамятных времён способом счёта предметов (так, если последний из пересчитываемых предметов окажется седьмым, то это и означает, что имеется семь предметов).

  Вопрос об обосновании понятия натурального Ч. долгое время в науке не ставился. Понятие натурального Ч. столь привычно и просто, что не возникало потребности в его определении в терминах каких-либо более простых понятий. Лишь в середине 19 в. под влиянием развития в математике, с одной стороны, и критического пересмотра основ математического анализа - с другой, назрела необходимость обоснования понятия количественного натурального Ч. Отчётливое определение понятия натурального Ч. на основе понятия множества (совокупности предметов) было дано в 70-х гг. 19 в. в работах Г. .Сначала он определяет понятие равномощности совокупностей. Именно, две совокупности называются равномощными, если составляющие их предметы могут быть сопоставлены по одному. Затем число предметов, составляющих данную совокупность, определяется как то общее, что имеет данная совокупность и всякая другая, равномощная ей совокупность предметов, независимо от всяких качественных особенностей этих предметов. Такое определение отражает сущность натурального Ч. как результата счёта предметов, составляющих данную совокупность. Действительно, на всех исторических уровнях счёт заключается в сопоставлении по одному считаемых предметов и предметов, составляющих «эталонную» совокупность (на ранних ступенях - пальцы рук и зарубки на палочке и т.д., на современном этапе - слова и знаки, обозначающие Ч.), Определение, данное Кантором, было отправным пунктом для обобщения понятия количеств. Ч. в направлении количественной характеристики бесконечных множеств.

  Другое обоснование понятия натурального Ч. базируется на анализе отношения порядка следования, которое, как оказывается, может быть аксиоматизировано. Построенная на этом принципе система аксиом была сформулирована Дж. .

 Следует отметить, что перенесение понятия порядкового Ч. на бесконечные совокупности [порядковые и более общо' - порядковые типы (см. )] резко расходится с обобщённым понятием количественного Ч.; это обусловлено тем, что количественно одинаковые (равномощные) множества могут быть упорядочены различными способами.

  Исторически первым расширением понятия Ч. является присоединение к натуральным Ч. дробных чисел. Введение в употребление дробных Ч. связано с потребностью производить измерения. Измерение какой-либо величины заключается в сравнении её с другой, качественно однородной с ней и принятой за единицу измерения. Это сравнение осуществляется посредством специфической для способа измерения операции «откладывания» единицы измерения на измеряемой величине и счёта числа таких откладываний. Так измеряется длина посредством откладывания отрезка, принятого за единицу измерения, количество жидкости - при помощи мерного сосуда и т.д. Однако не всегда единица измерения укладывается на измеряемой величине целое число раз, и этим обстоятельством, даже в самой примитивной практической деятельности, не всегда можно пренебречь. Здесь и содержится источник происхождения наиболее простых и «удобных» дробей, таких, как половина, треть, четверть и т.д. Но лишь с развитием арифметики как науки о Ч. созревает идея рассмотрения дробей с любым натуральным знаменателем и представление о дробном Ч. как о частном при делении двух натуральных Ч., из которых делимое не делится нацело на делитель (см. ) .

 Дальнейшие расширения понятия Ч. обусловлены уже не непосредственными потребностями счёта и измерения, но явились следствием развития математики.

  Введение отрицательных чисел было с необходимостью вызвано развитием алгебры как науки, дающей общие способы решения арифметических задач, независимо от их конкретного содержания и исходных числовых данных. Необходимость введения в алгебру отрицательного Ч. возникает уже при решении задач, сводящихся к линейным уравнениям с одним неизвестным. Возможный отрицательный ответ в задачах такого рода может быть истолкован на примерах простейших направленных величин (таких, как противоположно направленные отрезки, передвижение в направлении, противоположном выбранному, имущество - долг, и т.д.). В задачах же, приводящихся к многократному применению действий сложения и вычитания, для решения без помощи отрицательного Ч. необходимо рассмотрение очень многих случаев; это может быть настолько обременительным, что теряется преимущество алгебраического решения задачи перед арифметическим. Т. о., широкое использование алгебраических методов для решения задач весьма затруднительно без пользования отрицательного Ч. В Индии ещё в 6-11 вв. отрицательные Ч. систематически применялись при решении задач и истолковывались в основном так же, как это делается в настоящее время.

  В европейской науке отрицательные Ч. окончательно вошли в употребление лишь со времени Р. , давшего геометрическое истолкование отрицательного Ч. как направленных отрезков. Создание Декартом аналитической геометрии, позволившее рассматривать корни уравнения как координаты точек пересечения некоторой кривой с осью абсцисс, окончательно стёрло принципиальное различие между положительными и отрицательными корнями уравнения, их истолкование оказалось по существу одинаковым.

  Ч. целые, дробные (положительные и отрицательные) и нуль получили общее название рациональных чисел. Совокупность рациональных Ч. обладает свойством замкнутости по отношению к четырём арифметическим действиям. Это значит, что сумма, разность, произведение и частное (кроме частного при делении на нуль, которое не имеет смысла) любых двух рациональных Ч. является снова рациональным Ч. Совокупность рациональных Ч. упорядочена в отношении понятий «больше» и «меньше». Далее, совокупность рациональных Ч. обладает свойством плотности: между любыми двумя различными рациональными Ч. находится бесконечно много рациональных Ч. Это даёт возможность при помощи рациональных Ч. осуществлять измерение (например, длины отрезка в выбранной единице масштаба) с любой степенью точности. Т. о., совокупность рациональных Ч. оказывается достаточной для удовлетворения многих практических потребностей. Формальное обоснование понятий дробного и отрицательного Ч. было осуществлено в 19 в. и не представило, в отличие от обоснования натурального Ч., принципиальных затруднений.

  Совокупность рациональных Ч. оказалась недостаточной для изучения непрерывно изменяющихся переменных величин. Здесь оказалось необходимым новое расширение понятия Ч., заключающееся в переходе от множества рациональных Ч. к множеству действительных (вещественных) чисел. Этот переход состоит в присоединении к рациональным Ч. т. н. иррациональных чисел. Ещё в Древней Греции было сделано в геометрии открытие огромной принципиальной важности: не всякие точно заданные (что само по себе является присущей геометрии идеализацией) отрезки соизмеримы, т. е. не всегда длина отрезка может быть выражена рациональным Ч., если за единицу принят другой отрезок. Классическим примером несоизмеримых отрезков является сторона квадрата и его диагональ. Факт существования несоизмеримых отрезков не явился тормозом для развития геометрии. Греками была разработана (изложенная в «Началах» Евклида) теория отношений отрезков, учитывающая возможность их несоизмеримости. Они умели сравнивать такие отношения по величине, производить над ними арифметические действия (в чисто геометрической форме), т. е. греки обращались с такими отношениями, как с Ч. Однако идея о том, что отношение длин несоизмеримых отрезков может рассматриваться как Ч., у них не была осознана до конца. Это может быть объяснено культивировавшимся в школе, к которой принадлежал , идеалистическим отрывом теоретической математики от прикладных вопросов. В работах мы находим значительно бо'льшую близость к прикладным вопросам, в частности приближённые вычисления отношений несоизмеримых отрезков, однако и у него не появляется понятие иррационального Ч. как Ч., выражающего отношение длин несоизмеримых отрезков.

  В 17 в. в период зарождения современной науки и, в частности, современной математики разрабатывается ряд методов изучения непрерывных процессов и методов приближённых вычислений. Отчётливое определение понятия действительного Ч. даётся одним из основоположников математического анализа И. во «Всеобщей арифметике»: «Под числом мы понимаем не столько множество единиц, сколько отвлечённое отношение какой-нибудь величины к другой величине того же рода, принятой нами за единицу». Эта формулировка даёт единое определение действительного Ч., рационального или иррационального. В дальнейшем, в 70-х гг. 19 в., понятие действительного Ч. было уточнено на основе глубокого анализа понятия непрерывности в работах Р. , Г. Кантора и К. .

 По Дедекинду, свойство непрерывности прямой линии заключается в том, что если все точки, составляющие прямую, разбить на два класса так, что каждая точка первого класса лежит левее каждой точки второго класса («разорвать» прямую на две части), то либо в первом классе найдётся самая правая точка, либо во втором - самая левая точка, т. е. точка, в которой произошёл «разрыв» прямой.

  Совокупность всех рациональных Ч. свойством непрерывности не обладает. Если совокупность всех рациональных Ч. разбить на два класса так, что каждое Ч. первого класса будет меньше каждого Ч. второго класса, то при таком разбиении («сечении» Дедекинда) может оказаться, что в первом классе не будет существовать наибольшего Ч., а во втором - наименьшего. Так будет, например, если к первому классу отнести все отрицательные рациональные Ч., нуль и все положительные Ч., квадрат которых меньше двух, а ко второму - все положительные Ч., квадрат которых больше двух. Такое сечение называется иррациональным. Затем даётся следующее определение иррационального Ч.: каждому иррациональному сечению в совокупности рациональных Ч. сопоставляется иррациональное Ч., которое считается большим, чем любое Ч. первого класса, и меньшим, чем любое Ч. верхнего класса. Совокупность всех действительных Ч., рациональных и иррациональных, уже обладает свойством непрерывности.

  Обоснование Кантора понятия действительного Ч. отличается от обоснования Дедекинда, но также основывается на анализе понятия непрерывности. Как в определении Дедекинда, так и в определении Кантора используется абстракция актуальной бесконечности. Так, в теории Дедекинда иррациональное Ч. определяется посредством сечения в совокупности всех рациональных Ч., которая мыслится как данная вся целиком.

  В последние годы разрабатывается концепция «вычислимых» Ч., т. е. таких, приближения к которым могут быть заданы посредством какого-либо алгоритма. Понятие вычислимого Ч. определяется без пользования абстракцией актуальной бесконечности, на базе уточнённого понятия алгоритма.

  Заключительный этап в развитии понятия Ч. - введение .Источником возникновения понятия комплексного Ч. явилось развитие алгебры. По-видимому, впервые идея комплексного Ч. возникла у итальянских математиков 16 в. (Дж. Кардано, Р. Бомбелли) в связи с открытием алгебраического решения уравнений третьей и четвёртой степеней. Известно, что уже решение квадратного уравнения иногда приводит к действию извлечения квадратного корня из отрицательного Ч., невыполнимому в области действительного Ч. Но это происходит только в том случае, если уравнение не имеет действительных корней. Практическая задача, приводящаяся к решению такого квадратного уравнения, оказывается не имеющей решения. С открытием алгебраического решения уравнений третьей степени обнаружилось след. обстоятельство. Как раз в том случае, когда все три корня уравнения являются действительными Ч., по ходу вычисления оказывается необходимо выполнить действие извлечения квадратного корня из отрицательных Ч. Возникающая при этом «мнимость» исчезает только по выполнении всех последующих действий. Это обстоятельство явилось первым стимулом к рассмотрению комплексных Ч. Однако комплексные Ч. и действия над ними с трудом прививались в деятельности математиков. Остатки недоверия к закономерности пользования ими отражаются в сохранившемся до наших дней термине «мнимое» Ч. Это недоверие рассеялось лишь после установления в конце 18 в. геометрического истолкования комплексных Ч. в виде точек на плоскости и установления несомненной пользы от введения комплексных Ч. в теории алгебраических уравнений, особенно после знаменитых работ К. .Ещё до Гаусса, в работах Л. , комплексные Ч. начинают играть существенную роль не только в алгебре, но и в математическом анализе. Эта роль стала исключительно большой в 19 в. в связи с развитием теории функций комплексного переменного.

  Совокупность всех комплексных Ч. обладает так же, как совокупность действительных Ч. и совокупность рациональных Ч., свойством замкнутости по отношению к действиям сложения, вычитания, умножения и деления. Более того, совокупность всех комплексных Ч. обладает свойством алгебраической замкнутости, заключающейся в том, что каждое алгебраическое уравнение с комплексными коэффициентами имеет корни снова в области всех комплексных Ч. Совокупность всех действительных Ч. (и тем более рациональных) свойством алгебраической замкнутости не обладает. Так, например, уравнение с действительными коэффициентами х ²+1=0 не имеет действительных корней. Как установлено Вейерштрассом, совокупность всех комплексных Ч. не может быть далее расширена за счёт присоединения новых Ч. так, чтобы в расширенной совокупности сохранились все законы действий, имеющие место в совокупности комплексных Ч.

  Наряду с основной линией развития понятия Ч. (натуральные Ч. ® рациональные Ч. ® действительные Ч. ® комплексные Ч.), специфические потребности некоторых областей математики вызвали различные обобщения понятия Ч. в существенно других направлениях. Так, в разделах математики, связанных с теорией множеств, важную роль играют упоминавшиеся выше понятия количественных и порядковых трансфинитных Ч. В современной теории Ч. получили большое значение т. н. р-адические Ч., системы которых получаются из систем рациональных Ч. посредством присоединения новых объектов, отличных от иррациональных Ч. В алгебре изучаются различные системы объектов, обладающие свойствами, в большей или меньшей степени близкими к свойствам совокупности целых или рациональных Ч. - , , , алгебры (см. также ст. ) .

  Лит.:История математики, т. 1-3, М., 1970-72; Ван дер Варден Б. Л., Пробуждающаяся наука, пер. с голл., М., 1959; Энциклопедия элементарной математики, кн. 1 - Арифметика, М.-Л., 1951; Нечаев В. И., Числовые системы, М., 1972.

  Д. К. Фаддеев.

Число переноса

Число' перено'са,см. .

Числхерст-энд-Сидкап

Чи'слхерст-энд-Си'дкап(Chislehurst and Sidcup), город в Великобритании в составе метрополитенского округа Большого Лондона - Бексли.

Чисталёв Вениамин Тимофеевич

Чисталёв,Тима Вень Вениамин Тимофеевич [8(20).10.1890, с. Помоздино, ныне Коми АССР, - 13.10.1939, Сыктывкар], коми советский писатель. Родился в крестьянской семье. Учительствовал. Первые литературные опыты относятся к дореволюционному времени. В пейзажной лирике Ч. воспел коми край. Автор поэмы «В дни преображения земли» (1927) о героике социалистического строительства на Севере, первых очерков и рассказов на коми языке; переводил произведения русских писателей.

  Соч.: Олцм вояс. Бцрйцм гижцдъяс, Сыктывкар, 1957.

  Лит.:Микушев А. К., Коми литература и народная поэзия, Сыктывкар, 1961; Коми советские писатели, Сыктывкар, 1968.

Чистая линия

Чи'стая ли'ния,генотипически однородное потомство постоянно самоопыляющихся растений или самооплодотворяющихся животных, большая часть генов которого находится в гомозиготном состоянии. Термин введён в 1903 датским генетиком В. , который в опытах на бобовых растениях доказал, что в Ч. л. при одинаковых условиях проявляется сходный . Ч. л. получают от одного предка и поддерживают с помощью принудительного самоопыления и отбора. Особи в Ч. л. воспроизводят в ряду поколений одни и те же наследственно закрепленные признаки. Ч. л. имеют важное значение в с.-х. производстве, являясь основными структурными элементами сортов растений. Гибридизация двух Ч. л. в ряде случаев приводит к эффекту в первом гибридном поколении (так получают некоторые гибридные формы кукурузы). Иногда термин Ч. л. неправильно применяют к т. н. инбредным линиям, которые представляют собой потомство животных или растений (перекрёстноопыляющихся), получаемое от одной пары предков и поддерживаемое в ряду поколений с помощью постоянных близкородственных скрещиваний и отбора. Такие линии используют в подавляющем большинстве генетических исследований на высших организмах. Например, механизмы канцерогенеза и методы лечения раковых заболеваний изучаются на т. н. «Ч. л.» лабораторных мышей.

  И. И. Толсторуков.

Чистая прибыль

Чи'стая при'быль,в капиталистическом обществе - прибыль за вычетом налогов, используемая предпринимателями и монополиями для расширения производства и на паразитическое потребление. Масса Ч. п. зависит от массы валовой прибыли и величины налогов. Наличие коммерческой тайны, применение повышенных норм амортизации основного капитала и утончённых методов фальсификации отчётов позволяют капиталистам приуменьшать размеры Ч. п. и уплачиваемых налогов.

  Ч. п. социалистических предприятий - это балансовая прибыль, остающаяся после платежей из прибыли государству [плата за фонды, фиксированные (рентные) платежи, взносы свободного остатка прибыли, уплата процентов за кредит]. Ч. п. используется для образования , увеличения оборотных средств предприятия, финансирования части капитальных вложений.

Чистая продукция

Чи'стая проду'кция,часть валовой продукции, которая остаётся за вычетом потребленных в процессе производства средств производства (сырья, материалов, топлива, энергии, а также амортизации производственных основных фондов). С точки зрения образования стоимости Ч. п. представляет собой вновь созданную в отраслях материального производства стоимость ( v+ m). Сумма Ч. п. всех отраслей материального производства составляет общества.

  Ч. п. исчисляется по отдельным отраслям материального производства: промышленности, строительству, сельскому хозяйству и др. В промышленности она рассчитывается как разность между валовой продукцией и производственными материальными затратами. При этом валовая продукция промышленности берётся по ценам промышленности, т. е. с включением .Это необходимо для расчёта национального дохода и для составления .По отдельным отраслям промышленности и по предприятиям расчёты Ч. п. могут производиться и по оптовым ценам предприятий, т. е. без налога с оборота.

  Ч. п. строительства исчисляется как разность между валовой продукцией строительства (стоимость работ по новому строительству, расширению и реконструкции действующих предприятий и капитальному ремонту зданий и сооружений) и материальными затратами на строительство и капитальный ремонт зданий и сооружений (стоимость израсходованных строительных материалов, включая конструкции и детали, топлива, электроэнергии и других видов материальных затрат, а также амортизации строительных машин и других основных средств строительных организаций).

  Ч. п. сельского хозяйства представляет собой разность между валовой продукцией сельского хозяйства, исчисляемой по методу валового оборота (с включением стоимости собственной продукции, потребленной в своём хозяйстве), и производственными материальными затратами, в стоимость которых наряду с покупными сырьём и материалами включаются также продукты собственного производства (семена, корма). В других отраслях материального производства Ч. п. исчисляется как разность между валовой продукцией и производственными материальными затратами с учётом особенностей расчётов этих показателей в каждой отрасли.

  Ч. п. по отдельным отраслям материального производства исчисляется органами государственной статистики (ЦСУ СССР и ЦСУ союзных республик). Расчёты ведутся в фактически действующих в каждом году ценах и в сопоставимых ценах. Ч. п. в сопоставимых ценах характеризует динамику её развития и исчисляется вычитанием (в сопоставимых ценах) из валовой продукции производственных материальных затрат. Этот метод исчисления называется производственным. Ч. п. можно рассчитать и распределительным методом - как сумму заработной платы (и других видов оплаты труда), прибыли, налога с оборота и других элементов чистого дохода. Этот расчёт служит проверкой правильности исчисления Ч. п. производственным методом.

  В 1976 Ч. п. промышленности (включая налог с оборота) составляла 52,6% национального дохода, созданного в отраслях материального производства, сельского хозяйства - 16,5%, строительства - 11,2%, транспорта и связи - 6,3% и остальных отраслей - 13,4%.

  М. Р. Эйдельман.

Чистец

Чисте'ц(Stachys), род растений семейства губоцветных. Однолетние и многолетние травы или полукустарнички с супротивными цельными листьями. Цветки большей частю розовые, пурпуровые, белые или жёлтые, в ложных мутовках, образующих колосовидные соцветия; венчик с плоской или шлемовидной верхней губой. Плод из 4 орешковидных долей. Около 300 видов, в умеренном и субтропических поясах обоих полушарий и в горах тропиков. В СССР около 55 видов. Ч. болотный (S. palustris), растущий по влажным лугам, болотам, заболоченным лесам, берегам водоёмов, и Ч. однолетний (S. annua), встречающийся по сухим склонам, обрывам, пустырям, насыпям, - сорняки на полях, огородах, залежах. Ч. однолетний и Ч. прямой (S. recta), произрастающий по степным и каменистым склонам, считаются ядовитыми для лошадей. Ч. лесной (S. sylvatica) - растение тенистых широколиственных и смешанных лесов, кустарников, оврагов, сырых лугов. Ч. Зибольда, или японский и китайский артишок (S. sieboldii), распространённый в Китае и Японии, возделывается как овощ в Вост. Азии и в некоторых странах Европы и Америки; в пищу идут клубневидные образования на корнях, используемые в варёном, жареном и маринованном виде. Многие Ч. - медоносы. Ч. византийский (S. byzantina, прежде S. lanata) культивируют как декоративное растение.

Чистики

Чи'стики(Cepphus), род птиц семейства чистиковых. Длина тела 32-40 см, весят 340-600 г.Клюв чёрный, прямой и тонкий. Оперение взрослых летом чёрное, зимой пёстрое. Лапы красные. Ч. хорошо летают, плавают и ныряют; ходят плохо. Питаются мелкой рыбой и морскими беспозвоночными. Гнездятся группами, яйца откладывают в расщелинах скал, среди камней. В кладке обычно 2 яйца. Вылупившийся птенец покрыт густым мягким тёмным пухом. Покидает гнездо полностью оперившись. 2 (или 3) вида. Обыкновенный Ч. (С. grylle) обитает по побережьям Ледовитого и северных частей Атлантического и Тихого океанов; иногда Ч. с Тихого океана выделяют в отдельный вид - тихоокеанский Ч. (С. columba). Очковый Ч. (С. carbo) с белым пятном вокруг глаза, распространён по побережьям Охотского и Японского морей. Местами Ч. служат объектом промысла (используются мясо и яйца).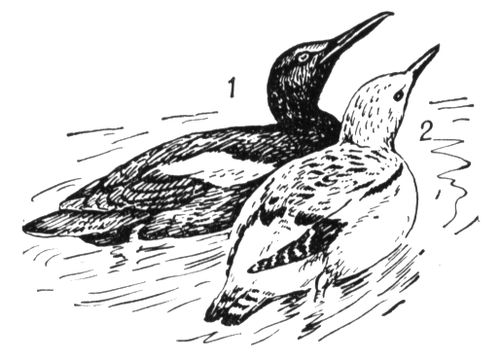

Обыкновенный чистик: 1 - взрослый, 2 - молодой.

Чистиковые

Чи'стиковые(Alcidae), семейство птиц отряда ржанкообразных. 13 родов: кайры, гагарки, конюги, люрики, пыжики, топорики, тупики, чистики и др.