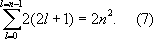Так, волокна и плёнки наиболее чувствительны к воздействию солнечной радиации, непрозрачные пластмассы — к действию тепла, резины — озона. Критерием А. п. м. служит изменение какого-либо эксплуатационного свойства материала за определённое время экспозиции или время экспозиции, за которое происходит определённое изменение этих характеристик (например, время до появления трещин, время до разрыва и т. д.). Выбор характеристики, по которой судят об А. п. м., определяется типом материала. Так, атмосферостойкость лакокрасочных покрытий оценивается по изменению их внешнего вида (блеска, цвета, степени растрескивания и др.) и защитных свойств.
А. п. м. во многом определяется интенсивностью воздействия атмосферных агентов и, следовательно, зависит от климата местности. Поэтому при оценке А. п. м. всегда учитывают климатическую зону, в которой проводилось испытание. Часто А. п. м. определяют не в естественных, а в лабораторных условиях ускоренными методами. Для этой цели пользуются различными приборами, например везерометрами, которые воспроизводят одновременно действие различных атмосферных агентов. А. п. м. сильно зависит от химической и физической структуры полимера и от характера введённых в него ингредиентов. Примеры полимерных Материалов с хорошей атмосферостойкостью —
и др. А. п. м. повышают различными
А'том(от греч. atomos — неделимый), частица вещества микроскопических размеров и очень малой массы (микрочастица), наименьшая часть химического элемента, являющаяся носителем его свойств. Каждому элементу соответствует определённый род А., обозначаемых символом элемента (например, А. водорода Н: А. железа Fe; А. ртути Hg; А. урана U).
А. могут существовать как в свободном состоянии, в газе, так и в связанном. Соединяясь химически с А. того же элемента или А. других элементов, они образуют более сложные микрочастицы —
, всё огромное многообразие химических соединений обусловлено различными сочетаниями А. в молекулах. Связываясь друг с другом непосредственно .или в составе молекул, А. образуют жидкости и твёрдые тела.
Свойства макроскопических тел — газообразных, жидких и твёрдых — и свойства отдельных молекул зависят от свойств входящих в их состав А. Все свойства А., физические и химические, определяются его строением как системы, состоящей из ядра и электронов, и подчиняются характерным для микроскопических явлений квантовым законам. Ниже излагаются современные представления о строении и свойствах А. (историю развития учения об А. см. в ст.
).
Общая характеристика строения атома.А. состоит из тяжёлого ядра, обладающего положительным электрическим зарядом, и окружающих его лёгких электронов с отрицательными электрическими зарядами, образующих электронные оболочки А. Размеры А. в целом определяются размерами его электронной оболочки и велики по сравнению с размерами ядра А.
Характерные порядки размеров:
Линейные размеры
Площадь*
Объем
Атом
10
—8
см
10
—16
см
2
10
—24
см
3
Ядро
10
—12
см
10
—24
см
2
10
—36
см
3
Отношение
10
4
10
8
10
12
* Поперечное сечение.
Электронные оболочки А. не имеют строго определённой границы; значения размеров А. в большей или меньшей степени зависят от способов их определения и весьма разнообразны (см.
).
Заряд ядра — основная характеристика А., обусловливающая его принадлежность определённому элементу. Заряд ядра всегда является целым кратным элементарного положительного электрич. заряда
е, равного по абсолютному значению заряду электрона
—е. Заряд ядра равен +
Ze, где
Z— порядковый номер (атомный номер).
Z= 1, 2, 3, 4,... для А. последовательных элементов в периодической системе элементов Менделеева, т. е. для атомов Н, Не, Li, Be, ...В нейтральном А. ядро с зарядом +
Zeудерживает
Zэлектронов с общим зарядом —
Zeи полный заряд А. равен нулю; в положительном ионе —А., потерявшем
kэлектронов (ионизованном А.), остаётся Z—
kэлектронов (
k= 1, 2, 3, ... — кратность ионизации) и его заряд равен +
ke, в отрицательном ионе —А., присоединившем
kэлектронов,— содержится
Z+
kэлектронов, и его заряд равен —
ke. Для положительного иона максимальное значение
k=
Z(такой ион потерял все свои электроны и состоит из «голого» ядра); для отрицательного свободного иона
k= 1, для связанных А. возможно образование отрицательных ионов с
k> 1 (в растворах,
и
). Говоря об А. определённого элемента, подразумевают как нейтральные А., так и ионы этого элемента. Но иногда под А. понимают нейтральный А., в противоположность ионам. Положительные и отрицательные ионы при написании отличают от нейтрального А. индексом
k+ и
k—, например О обозначает нейтральный А. кислорода (
Z= 8), О
+, О
2+(или O
++), O
3+,..., O
8+— его положительные ионы,О
—, O
2—(или О
—— его отрицательные ионы. Совокупность нейтрального А. и ионов других элементов с тем же числом электронов образует изоэлектронный ряд. Простейший такой ряд начинается с А. водорода: H, He
+, Li
2+, Be
3+, ...; члены этого ряда состоят из ядра и одного электрона.
Порядок значений зарядов ядер различных А. был определён английским физиком Э. Резерфордом в его первоначальных опытах по рассеянию альфа-частиц (1911). Значения
Zбыли надёжно установлены английским физиком Г. Мозли (1913—14) на основе изучения рентгеновских спектров последовательных элементов в периодической системе. Кратность заряда ядра А. элементарному заряду
еполучила объяснение, исходя из представлений о строении ядра:
Zравно числу
в ядре, протон имеет заряд +
е, и полный заряд ядра равен сумме зарядов всех
Zпротонов, т. е. +
Ze.
Масса атома возрастает с увеличением
Z. Масса ядра А. приближённо пропорциональна
А — общему числу протонов и нейтронов в ядре. Масса электрона (0,91 10
—27
г) значительно меньше (примерно в 1840 раз) массы протона или нейтрона (1,67 10
—24
г), и поэтому масса А. в целом определяется в основном массой его ядра.
А. данного элемента могут отличаться массой ядра (число протонов
Zпостоянно, число нейтронов
А—Zможет меняться); такие разновидности А. одного и того же элемента называются
. Различие массы ядра почти не сказывается на строении их электронных оболочек, зависящем от заряда ядра
Z. Химические и большинство физических свойств (оптические, электрические, магнитные), определяемые строением электронных оболочек, одинаковы или очень близки для всех изотопов данною элемента. Наибольшие отличия в свойствах (изотонические эффекты) получаются для изотопов водорода (
Z= 1) из-за большой разницы в массах обычного лёгкого А. водорода (
А= 1), А. дейтерия (
А= 2) и А. трития (
А= 3).
Масса А. приближённо равна массовому числу
Аи изменяется от 1,67 10
—24
гдля самого лёгкого А. водорода (основного изотопа:
Z= 1,
A= 1) до примерно 4 10
—22
гдля самых тяжёлых А. трансурановых элементов (
Z= 100,
А= 250).
Наиболее точные значения масс А. могут быть определены методами
. Масса А. не равна в точности сумме массы ядра и масс электронов, а несколько меньше — на
D
М = W/c
2',где
W —энергия образования А. из ядра и электронов, а
с —скорость света. Эта поправка — порядка массы одного электрона
m
едля тяжёлых А., а для лёгких А. пренебрежимо мала (порядка 10
—4массы электрона).
Энергия атома и её квантование. Благодаря малым размерам и большой массе ядра его можно приближённо считать точечным и покоящимся в центре масс А. (общий центр масс ядра и электронов находится вблизи ядра, а скорость движения ядра относительно центра масс А. мала по сравнению со скоростями движения электронов). Соответственно А. можно рассматривать как систему, в которой
Nэлектронов с зарядами —
едвижутся вокруг неподвижного притягивающего центра. Движение электронов в А. происходит в ограниченном объёме — оно является связанным. Полная внутренняя энергия А.
Еравна сумме кинетических энергий всех электронов
Ти потенциальной энергии
U —энергии притяжения их ядром и отталкивания их друг от друга (электростатической энергии взаимодействия электрических зарядов ядра и электронов, согласно закону Кулона).
В простейшем случае А. водорода один электрон с зарядом —
едвижется вокруг неподвижного центра с зарядом +
е. В этом случае, согласно классической механике, кинетическая энергия
Т =
1/
2
mv =p
2/2
m (1)
где
m —масса,
v —скорость,
p = mv —количество движения (импульс) электрона. Потенциальная энергия (сводящаяся к энергии притяжения электрона ядром)
U = U(
r)
= —e
2/r (2)
и зависит только от расстояния
rэлектрона от ядра. Графически функция
U(
r)
изображается кривой (
рис. 1
, а)
,неограниченно убывающей при уменьшении
r, т. е. при приближении электрона к ядру. Значение
U(
r) на бесконечности принято за нуль. При отрицательных значениях полной энергии
Е=
Т + U< 0 движение электрона является связанным: оно ограничено в пространстве значениями
r=
r
max, при которых
Т= 0,
Е = U(
r
max)
.При положительных значениях полной энергии
E = T + U> 0
движение электрона является свободным — он может уйти на бесконечность с энергией
Е = Т =
1/
2mv
2,что соответствует ионизованному А. водорода Н
+. Нейтральный А. водорода Н представляет, т. о., систему, состоящую из ядра и электрона в связанном состоянии с энергией
E
<0.
Полная внутренняя энергия А.
Еявляется его основной характеристикой как квантовой системы — системы, подчиняющейся квантовым законам (см.
). Как показывает огромный экспериментальный материал (см., например,
)
,А. может длительно находиться лишь в состояниях с определённой энергией — стационарных (неизменных во времени) состояниях.
Существование стационарных состояний — один из основных законов физики микроскопических явлений — квантовой физики. Внутренняя энергия квантовой системы, состоящей из связанных микрочастиц (такой системой и является А.), может принимать одно из дискретного (прерывного) ряда значений
E
1, E
2, E
3, ...(
E
1< E
2< E
3< ...)
. (3)
Каждому из этих «дозволенных» значений энергии соответствует одно или несколько стационарных квантовых состояний движения. Промежуточными значениями энергии (например, лежащими между
E
1и
E
2, E
2и
E
3и т.д.) система обладать не может, о такой системе говорят, что её энергия квантована, а нахождение возможных значений энергии называется квантованием энергии. Любое изменение энергии
Есвязано с квантовым (скачкообразным) переходом системы из одного стационарного квантового состояния в другое (см. ниже).
Графически возможные дискретные значения энергии (3) А. можно изобразить, по аналогии с потенциальной энергией тела, поднятого на различные высоты (на различные уровни), в виде схемы
,где каждому значению энергии соответствует прямая, проведённая на высоте
E
i(
i =1, 2, 3, ...); такая схема приведена на
рис. 1
, б для А. водорода (на
рис. 1
, а при
E< 0 оказываются, т. о., возможными лишь определённые ступеньки, соединённые горизонтальным пунктиром с уровнями схемы на рис. 1, б). Самый нижний уровень
E
i,соответствующий наименьшей возможной энергии системы, называется основным, а все остальные (
E
i
> Ei,
г= 2, 3, 4, ...) — возбуждёнными, т. к. для перехода на них (перехода в соответствующие стационарные возбуждённые состояния из стационарного основного состояния) необходимо возбудить систему — сообщить ей извне энергию
E
i—E
1.
Квантование энергии А. является следствием волновых свойств электронов. Нельзя считать, что электрон в А. движется как материальная точка по определённой траектории, согласно законам классической механики. Эти законы справедливы лишь для частиц большой массы (макрочастиц), а для электрона, как микрочастицы, необходимо учитывать, наряду с его корпускулярными свойствами (свойствами частицы), и его волновые свойства. Согласно квантовой механике, движению микрочастицы массы
mсо скоростью
vсоответствует длина волны l
= h/mv,где
h —
.Для электрона в А. l
~10
—8
см,т. е. порядка линейных размеров А., и учёт волновых свойств электрона в А. является необходимым. Связанное движение электрона в А. схоже со
,и его следует рассматривать не как движение материальной точки по траектории, а как сложный колебательный процесс. Для стоячей волны в ограниченном объёме возможны лишь определённые значения длины волны l (и, следовательно, частоты колебаний
v). Так как, согласно квантовой механике,
v
= E/h,отсюда следует, что система, состоящая, подобно А., из связанных микрочастиц, может иметь лишь определённые значения энергии, т. е. энергия квантуется и получается дискретная последовательность уровней энергии — дискретный энергетический спектр. Для А. водорода такая дискретная последовательность получается при
Е< 0 (см.
рис. 1
). Свободное, т. е. не ограниченное в пространстве, поступательное движение микрочастицы, например движение электрона, оторванного от А. (в случае А. водорода — электрона с энергией
Е> 0)
,сходно с распространением бегущей волны в неограниченном объёме, для которой возможны любые значения l (и
v). Энергия такой свободной микрочастицы может принимать любые значения, т. е. не квантуется, и получается непрерывная последовательность уровней энергии — непрерывный энергетический спектр. Для А. водорода такая непрерывная последовательность, соответствующая ионизованному А., получается при
E> 0. Значение
Е
Ґ= 0 соответствует границе ионизации, а разность
Е
Ґ—
Е
1=
Е
ионпредставляет энергию ионизации: для А. водорода она равна 13,6
эв.
Распределение электронной плотности. Состояние электрона в А. можно характеризовать распределением в пространстве его электрического заряда с некоторой плотностью — распределением электронной плотности. При этом электроны рассматриваются наглядным образом, как «размазанные» в пространстве и образующие «электронное облако». Такая модель правильнее характеризует электроны в А., чем модель точечного электрона, движущегося, согласно теории Бора (см.
)
,по строго определённым орбитам. Вместе с тем боровским орбитам можно сопоставить определённые распределения электронной плотности. Для основного уровня энергии
Е
1электронная плотность концентрируется вблизи ядра; для возбуждённых уровней энергии
E
2, E
3, E
4,... она распределяется на всё больших средних расстояниях от ядра (что соответствует возрастанию размера орбит в теории Бора). В сложном А. эти электроны группируются в оболочки, окружающие ядро на различных расстояниях и характеризующиеся определёнными распределениями электронной плотности. Прочность связи электронов в более внешних оболочках меньше, чем во внутренних, и слабее всего электроны связаны в самой внешней оболочке, обладающей наибольшими размерами, которые и определяют размеры А. в целом. При ионизации А. теряет внешние электроны; размеры положительных ионов тем меньше размеров нейтрального А., чем выше кратность иона. Наоборот, размеры отрицательных ионов больше размеров нейтрального А.
Учёт спина электрона и спина ядра. В теории А. весьма существен учёт
электрона — его собственного (спинового) момента количества движения, с наглядной точки зрения соответствующего вращению электрона вокруг собственной оси (если электрон рассматривать как частицу малых размеров). Со спином электрона связан его
.Поэтому в А. необходимо учитывать, наряду с электростатическими взаимодействиями (см. выше), и магнитные взаимодействия, определяемые спиновым магнитным моментом, а также орбитальным магнитным моментом, связанным с движением электрона вокруг ядра; магнитные взаимодействия малы по сравнению с электростатическими. Наиболее существенное влияние спина проявляется в сложных А.: от спина электронов зависит заполнение электронных оболочек А. определённым числом электронов (см. ниже).
Ядро в А. также может обладать собственным механическим моментом — ядерным спином, с которым связан небольшой ядерный магнитный момент (в сотни и тысячи раз меньший электронного магнитного момента), а в некоторых случаях и т. н. квадрупольный электрический момент (см.
)
.Это приводит к дополнительным очень малым взаимодействиям ядра и электронов, обусловливающим дополнительное расщепление уровней энергии А. — т. н.
(малую по сравнению с тонкой структурой).
Квантовые состояния атома водорода.Важнейшую роль в квантовой теории А. играет теория простейшего одноэлектронного А., состоящего из ядра с зарядом +
Zeи электрона с зарядом —
е, —теория А. водорода Н и водородоподобных ионов Не
+, Li
2+, Ве
3+,... (изоэлектронного ряда, см. выше), называется обычно теорией А. водорода. Методами квантовой механики можно получить точную и полную характеристику состояний электрона в одноэлектронном А. Задача о сложных (многоэлектронных) атомах решается лишь приближённо; при этом исходят из результатов решения задачи об одноэлектронном А.
Уровни энергии А. водорода и водородоподобных ионов. Энергия одноэлектронного А. (без учёта спина электрона) равна
целое число
n =1, 2, 3, ... определяет возможные дискретные значения энергии — уровни энергии; его называют главным квантовым числом.
R—
,равная 13,6
эв.Уровни энергии А. водорода на схеме
рис. 1
, б построены для
Z= 1 согласно формуле (4); они сгущаются (сходятся) к границе ионизации
Е
Ґ= 0, соответствующей
n =Ґ
(уровни энергии с
n> 5 на схеме не показаны). Для водородоподобных ионов изменяется (в
Z
2раз) лишь масштаб энергий. Энергия ионизации водородоподобного А. (энергия связи электрона в таком А.) равна (в
эв)
Е
ион= E
Ґ
— E
1= RZ
2= 13,6Z
2 (5)
что даёт для Н, Не
+, Li
2+, ... значения 13,6
эв, 54,4
эв, 122,4
эв, ...
Основная формула (4) соответствует выражению
U(
r)
= —Ze
2/rдля потенциальной энергии электрона, притягиваемого ядром с зарядом
+Ze[см. (2) и
рис. 1
, а для случая
Z= 1]. Эта формула была впервые выведена Н. Бором в его теории А. (1913) путём рассмотрения движения электрона вокруг ядра по круговой орбите радиуса
r. Уровням энергии (4) соответствуют орбиты радиуса
a
nZ=
a
0
n
2/
Z (6)
где постоянная
a
0= 0,529 10
—8
см= 0,529
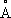
— радиус первой круговой орбиты А. водорода, соответствующей его основному уровню (этим боровским радиусом часто пользуются в качестве удобной единицы для измерений длин в атомной физике). Радиус орбит пропорционален квадрату главного квантового числа
n
2и обратно пропорционален
Z; для водородоподобных ионов масштаб линейных размеров уменьшается в
Zраз по сравнению с А. водорода.
Характеристика квантовых состояний атома водорода. Согласно квантовой механике, состояние А. водорода полностью определяется дискретными значениями четырёх физических величин: энергии
Е,орбитального момента
M
l,(момента количества движения электрона относительно ядра); проекции
M
lzорбитального момента на направление
z(выбранное произвольно в пространстве); проекции
M
szспинового момента (собственного момента количества движения электрона
M
s)
.Возможные значения этих физических величин, в свою очередь, определяются соответствующими квантовыми числами:
1) Е — по закону (4) — главным квантовым числом
n=1, 2, 3, ...;
2)
М
l—по закону
M
l
2=(
h
2/4p
2
)
l(
l+ 1)
[при
l" 1,
M
l
2=(
h
2/4p
2
)
l
2—орбитальным (или азимутальным) квантовым числом
l= 0,1, 2, ...,
n—1;
3)
M
lz—по закону
M
lz=(
h/2p)
m
lz—магнитным орбитальным квантовым числом
m
l= l, l—1, ..., —
l;
4)
M
sz—по закону
M
sz=(
h/2p)
m
s—магнитным спиновым квантовым числом
m
s
=
1/
2, —
1/
2
.
Значения квантовых чисел
n, l, m
l, m
sи характеризуют состояние электрона в А. водорода. Энергия А. водорода зависит только от
n,и уровню энергии с заданным
nсоответствует ряд состояний, отличающихся значениями
l,
m
lи
m
s.Состояния с заданными значениями
nи
lпринято обозначать как 1
s,2
s,2
p,3
s,..., где цифры указывают значение
n,а буквы
s, р, d, f(дальше по латинскому алфавиту) — соответственно значения
l= 0, 1, 2, 3, ... При заданных
nи
lчисло различных состояний равно 2(2
l+ 1) — числу комбинаций значений
m
lи
m
s(первое принимает 2
l+ 1 значение, второе — 2 значения). Общее число различных состояний с заданными
nи
lпри учёте, что
lможет принимать значения от 0 до
n—1, получается равным
Т. о., каждому уровню энергии А. водорода соответствует 2, 8, 18, ...,
2n
2(при
n =1, 2, 3, ...) различных стационарных квантовых состояний (
рис. 2
). Если уровню энергии соответствует лишь одно квантовое состояние, то его называют невырожденным, если два или более — вырожденным (см.
)
,а число таких состояний
gназываются степенью или кратностью вырождения (для невырожденных уровней энергии
g= 1). Уровни энергии А. водорода являются вырожденными, а их степень вырождения g
n=2
n
2.
Для различных состояний А. водорода получается и различное распределение электронной плотности. Оно зависит от квантовых чисел
n, lи /
m
i/
.При этом электронная плотность для
s-cocтояний (
l= 0) отлична от нуля в центре, т. е. в месте нахождения ядра, и не зависит от направления (сферически симметрична), а для остальных состояний (
l> 0) она равна нулю в центре и зависит от направления. Распределение электронной плотности для состояний А. водорода с
n =1, 2 и 3 показано на
рис. 3
(оно получено фотографированием специальных моделей); размеры «электронного облака» растут примерно пропорционально
n
2(масштаб на
рис. 3
уменьшается при переходе от
n= 1 к
n= 2 и от
n= 2 к
n= 3)
,что соответствует увеличению радиуса орбит по формуле (6) в теории Бора.
Квантовые состояния электрона в водородоподобных ионах характеризуются теми же четырьмя квантовыми числами
n, l, m
lи
m
s,что и в А. водорода. Сохраняется и распределение электронной плотности, только она увеличивается в
Zраз и на
рис. 3
масштабы нужно уменьшить также в
Zраз. Соответственно уменьшаются и размеры орбит.
Действие внешних полей на уровни энергии атома водорода. Во внешнем электрическом и магнитном полях А. как электрическая система приобретает дополнительную энергию. Электрическое поле поляризует А. — смещает электронное облако относительно ядра, а магнитное поле ориентирует определённым образом магнитный момент А., связанный с движением электрона вокруг ядра (с орбитальным моментом
M
l) и его спином. Различным состояниям А. водорода с той же энергией
Е
nво внешнем поле соответствует различная дополнительная энергия D
Eи вырожденный уровень энергии
Е
nрасщепляется на ряд подуровней (
рис. 4
). Как расщепление в электрическом поле —
,так и расщепление в магнитном поле —
,для уровней энергии А. водорода пропорциональны напряжённости полей.
К расщеплению уровней энергии приводят и малые магнитные взаимодействия внутри А. Для А. водорода и водородоподобных ионов имеет место спин-орбитальное взаимодействие — взаимодействие спинового и орбитального моментов электрона, не учитываемое при выводе основной формулы (4); оно обусловливает т.н. тонкую структуру уровней энергии — расщепление возбуждённых уровней
Е
n(при
n> 1) на подуровни. Наиболее точные исследования тонкой структуры методами радиоспектроскопии показали наличие т. н. сдвига уровней, объясняемого в квантовой электродинамике.
Для всех уровней энергии А. водорода наблюдается и сверхтонкая структура, обусловленная очень малыми магнитными взаимодействиями ядерного спина с электронными моментами. Уровень
E
1расщепляется на 2 подуровня с расстоянием между ними примерно 5 10
—6
эв.
Электронные оболочки сложных атомов.Теория сложных А., содержащих 2 или более электронов, принципиально отличается от теории А. водорода, т. к. в сложном А. имеются взаимодействующие друг с другом одинаковые частицы — электроны.


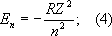
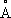 — радиус первой круговой орбиты А. водорода, соответствующей его основному уровню (этим боровским радиусом часто пользуются в качестве удобной единицы для измерений длин в атомной физике). Радиус орбит пропорционален квадрату главного квантового числа
n
2и обратно пропорционален
Z; для водородоподобных ионов масштаб линейных размеров уменьшается в
Zраз по сравнению с А. водорода.
— радиус первой круговой орбиты А. водорода, соответствующей его основному уровню (этим боровским радиусом часто пользуются в качестве удобной единицы для измерений длин в атомной физике). Радиус орбит пропорционален квадрату главного квантового числа
n
2и обратно пропорционален
Z; для водородоподобных ионов масштаб линейных размеров уменьшается в
Zраз по сравнению с А. водорода.