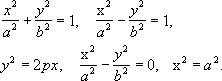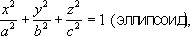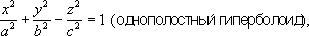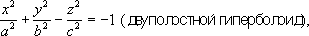Анализатор

Анализа'торв оптике, устройство для анализа характера поляризации света. Для обнаружения плоско-поляризованного света и определения его плоскости поляризации применяют поляризационные призмы, поляроиды и пластинки турмалина. Подробнее см. .

Анализатор звука

Анализа'тор зву'ка,прибор для анализа звука (разложения сложных звуковых сигналов на элементарные составляющие) по частоте или во времени. В соответствии с этим А. з. делятся на частотные и временные. См. .

Анализатор спектра

Анализа'тор спе'ктрачастот, измерительный прибор лабораторного применения для исследования частотных спектров, наблюдаемых на экране электроннолучевой трубки (ЭЛТ), импульсно- и амплитудно-модулированных колебаний в 3- и 10 -смдиапазонах волн. Для получения осциллографического изображения спектра исследуемых колебаний в координатах «мощность - частота» в А. с. применяют ,в котором подаваемые на вход колебания ослабляются (если необходимо) ,преобразуются по частоте, усиливаются и затем поступают на вертикальные отклоняющие пластины ЭЛТ; частота гетеродина приёмника линейно изменяется на ± 8 Мгц(в 10- смдиапазоне) или на ±30 Мгц(в 3 -смдиапазоне) в такт с пилообразным напряжением развёртки, одновременно подаваемым в цепи, изменяющие частоту гетеродина, и на горизонтальные пластины ЭЛТ. В А. с. предусмотрена градуировка по частоте, осуществляемая генератором калибровочных меток с плавной регулировкой амплитуды и частоты от 1 до 10 Мгц.А. с. можно измерять уход частоты генератора, малые разности частот двух генераторов и др.

  Лит.:Шкурин Г. П., Справочник по электроизмерительным и радиоизмерительным приборам, 3 изд., т. 2, М., 1960.

Анализаторы

Анализа'торы(биологические), сложные анатомо-физиологические системы, обеспечивающие восприятие и анализ всех раздражителей, действующих на животных и человека.

  Биологическая роль А. заключается в обеспечении целесообразной реакции организма на изменение условий, что способствует наиболее совершенному приспособлению его к окружающему миру и сохранению относительного постоянства внутренней среды организма (см. ) .

 Понятие об А. введено в физиологию русским физиологом И. П. в 1909. Метод дал возможность объективного изучения анализаторной деятельности животных и человека. Учение об А. послужило естественнонаучной основой диалектико-материалистического представления об ощущении, которое, по выражению В. И. Ленина, «...есть действительно непосредственная связь сознания с внешним миром, есть превращение энергии внешнего раздражения в факт сознания» (Полн. собр. соч., 5 изд., т. 18, с. 46).

  Каждый А. состоит из периферического воспринимающего прибора ( ) ,проводниковой части А., передающей информацию, и высшего центра А. - группы нейронов в коре головного мозга. К воспринимающим приборам А. относятся все органы чувств (зрения, слуха, вкуса и др.) и специальные рецепторные образования в органах, тканях, суставах, сосудах и мышцах. Для рецепторных приборов, благодаря особенностям их строения, характерна приспособленность к восприятию определённых видов раздражения и высокая чувствительность к ним. Проводниковая часть А. состоит из периферического нерва и нервных клеток («вставочных» ) .Эти клетки расположены в центральной нервной системе (за исключением первых двух нейронов зрительного, обонятельного и слухового А., расположенных на периферии, в соответствующих органах чувств). Анализ действующих на организм раздражителей начинается на периферии: каждый рецептор реагирует на определённый вид энергии, анализ продолжается во вставочных нейронах; так, на уровне нейронов зрительного А., расположенных в ,возможно различение местоположения предмета, его цвета. Но только в высших центрах А. - в коре больших полушарий головного мозга - осуществляется тонкий, дифференцированный анализ сложных, меняющихся раздражителей внешней среды. А. играют важную роль в регуляции и саморегуляции деятельности органов, физиологических систем и целостного организма. Анализаторная функция мозга животных и человека находится в тесном взаимодействии с его синтетической функцией и характеризуется высокой чувствительностью, тонкой дифференцировкой восприятий и широкой к меняющимся по силе и качеству раздражениям. Аналитико-синтетическая деятельность больших полушарий мозга служит основой .См. также , , .

 Изучение деятельности А. имеет большое теоретическое и практическое значение для физиологии, философии, психологии, медицины, а также для технического прогресса, в плане которого изучением А. занимается .Как расположить приборы на пульте управления, какого цвета, формы, размера, частоты, силы должны быть сигналы, чтобы они скорее и точнее воспринимались человеком (лётчиком, космонавтом, диспетчером, оператором и др.), какова предельная способность восприятия в разных условиях, как меняется эта способность при изменении условий или состояния человека - эти проблемы тесно связаны с изучением А. Так, учёт возможностей разных А. при разработке тех или иных измерительных или сигнальных устройств позволил определить условия наилучшего их наблюдения, в том числе оптимальные размеры и форму шкал, экранов и пр., их расположения на панели и т. д.

  Лит.:Павлов И. П., Полн. собр. соч., 2 изд., т. 4, М., 1951, с. 122-44; Черниговский В. Н., Интероцепторы, М., 1962; Гамбарян Л. С., Вопросы физиологии двигательного анализатора, М., 1962.

  Г. Н. Кассиль.

Анализирующее скрещивание

Анализи'рующее скре'щивание,скрещивание гибрида с родительской формой, имеющей рецессивные признаки (гомозиготной по рецессивным ) .См. .

Аналитическая геометрия

Аналити'ческая геоме'трия,раздел геометрии. Основными понятиями А. г. являются простейшие геометрические образы (точки, прямые, плоскости, кривые и поверхности второго порядка). Основными средствами исследования в А. г. служат метод координат (см. ниже) и методы элементарной алгебры. Возникновение метода координат тесно связано с бурным развитием астрономии, механики и техники в 17 в. Отчётливое и исчерпывающее изложение этого метода и основ А. г. было сделано P. в его «Геометрии» (1637). Основные идеи метода были известны также его современнику П. .Дальнейшая разработка А. г. связана с трудами Г. ,И. и особенно Л. .Средствами А. г. пользовался Ж. при построении аналитической механики и Г. в дифференциальной геометрии. Ныне А. г. не имеет самостоятельного значения как наука, однако её методы широко применяются в различных разделах математики, механики, физики и др. наук.

  Сущность метода координат заключается в следующем. Рассмотрим, например, на плоскости p две взаимно перпендикулярные прямые Oxи Оу( рис. 1 ). Эти прямые с указанным на них направлением, началом координат О и выбранной масштабной единицей е образуют т. н. декартову прямоугольную систему координат Охуна плоскости. Прямые Oxи Оуназываются соответственно осью абсцисс и осью ординат. Положение любой точки Мна плоскости по отношению к этой системе Охуможно определить следующим образом. Пусть M _xи M _y- проекции Мна Ox: и Оу,а числа хи y -величины отрезков OM _xи ОМ _у (величина хотрезка OM _x,например, равна длине этого отрезка, взятой со знаком плюс, если направление от Ок M _xсовпадает с направлением на прямой Ox,и со знаком минус в противоположном случае). Числа хи уназываются декартовыми прямоугольными координатами точки Мв системе Оху.Обычно они называются соответственно абсциссой и ординатой точки M.Для обозначения точки Мс абсциссой хи ординатой упользуются символом М( х,у) .Ясно, что координаты точки Мопределяют её положение относительно системы Оху.

 Пусть на плоскости p с данной декартовой прямоугольной системой координат Охузадана некоторая линия L.Используя понятие координат точек, можно ввести понятие уравнения данной линии Lотносительно системы Охукак соотношения вида F( x,y) = 0, которому удовлетворяют координаты хи улюбой точки M,расположенной на L,и не удовлетворяют координаты каждой точки, не лежащей на L.Если, например, линия Lявляется окружностью радиуса R сцентром в начале координат O, то уравнение x ²+ y ²- R ²=0 будет уравнением рассматриваемой окружности, в чём можно убедиться, обратившись к рис. 2 . Если точка Млежит на окружности, то по теореме Пифагора для треугольника OMM _xполучается x ²+ y ²- R ²= 0.Если же точка не лежит на окружности, то, очевидно, x ²+ y ²- R ²¹ 0.Итак, линии Lна плоскости можно сопоставить её уравнение F( x,y) =0 относительно системы координат Оху.

 Основная идея метода координат на плоскости состоит в том, что геометрические свойства линии Lвыясняются путём изучения аналитическими и алгебраическими средствами свойств уравнения F( x,y) =0 этой линии. Например, применим метод координат для выяснения числа точек пересечения окружности С радиуса Rи данной прямой линии В  ( рис. 3 ). Пусть начало системы координат Охунаходится в центре окружности, а ось Oxнаправлена перпендикулярно прямой В.Так как прямая Вперпендикулярна оси Ox,то абсцисса любой точки этой прямой равна некоторой постоянной a.Т. о., уравнение прямой Вимеет вид x - a= 0. Координаты ( x, y) точки пересечения окружности С (ур-ние которой имеет вид x ²+ y ²- R ²= 0) и прямой Вудовлетворяют одновременно уравнениям

  x ²+ y ²- R ²=0, х - а = 0,(1)

то есть являются решением системы (1). Следовательно, геометрический вопрос о числе точек пересечения прямой и окружности сводится к аналитическому вопросу о числе решений алгебраической системы (1). Решая эту систему, получают х = a, у = ± R ²- a ².Итак, окружность и прямая могут пересекаться в двух точках ( R ²> a ²) (этот случай изображен на рис. 3 ), могут иметь одну общую точку ( R ²= a ²) (в этом случае прямая Вкасается окружности C) и не иметь общих точек ( R ²< a ²) (в этом случае прямая Влежит вне окружности C).

  В А. г. на плоскости подробно изучаются геометрические свойства , и ,представляющих собой линии пересечения кругового конуса с плоскостями, не проходящими через его вершину (см. ) .Эти линии часто встречаются во многих задачах естествознания и техники. Например, движение материальной точки под воздействием центрального поля силы тяжести происходит по одной из этих линий; в инженерном деле для конструирования прожекторов, антенн и телескопов пользуются важным оптическим свойством параболы, заключающимся в том, что лучи света, исходящие из определённой точки (фокуса параболы), после отражения от параболы образуют параллельный пучок.

  В А. г. на плоскости систематически исследуются т. н. алгебраические линии первого и второго порядков (эти линии в декартовых прямоугольных координатах определяются соответственно алгебраическими уравнениями первой и второй степени). Линии первого порядка суть прямые, и обратно, каждая прямая определяется алгебраическим уравнением первой степени Ax + By+ С = 0. Линии второго порядка определяются уравнениями вида Ax ²+ Вху + Су ²+ Dx + Еу+ F= 0. Основной метод исследования и классификации этих линий заключается в подборе такой декартовой прямоугольной системы координат, в которой уравнение линии имеет наиболее простой вид, и последующем исследовании этого простого уравнения. Можно доказать, что таким способом уравнение любой вещественной линии второго порядка может быть приведено к одному из следующих простейших видов:

 Первое из этих уравнений определяет эллипс, второе - гиперболу, третье - параболу, а последние два - пару прямых (пересекающихся, параллельных или слившихся).

  В А. г. в пространстве также пользуются методом координат. При этом декартовы прямоугольные координаты . x, уи z(абсцисса, ордината и апликата) точки Мвводятся в полной аналогии с плоским случаем ( рис. 4 ). Каждой поверхности S в пространстве можно сопоставить её уравнение F( x, y, z) =0 относительно системы координат Oxyz.(Так, например, уравнение сферы радиуса Rс центром в начале координат имеет вид x ²+ y ²+ z ²- R ²= 0.) При этом геометрические свойства поверхности Sвыясняются путём изучения аналитическими и алгебраическими средствами свойств уравнения этой поверхности. Линию Lв пространстве задают как линию пересечения двух поверхностей S ₁и S ₁.Если F ₁( x, y, z) = 0 и F ₂( x, y, z) =0 - уравнения S ₁и S ₂, то пара этих уравнений, рассматриваемая совместно, представляет собой уравнение линии L.Например, прямую Lв пространстве можно рассматривать как линию пересечения двух плоскостей. Так как плоскость в пространстве определяется уравнением вида Ax+ By + Cz+ D= 0, то пара уравнений такого вида, рассматриваемая совместно, представляет собой уравнение прямой L.Т. о., метод координат может применяться и для исследования линий в пространстве. В A. г. в пространстве систематически исследуются т. н. алгебраические поверхности первого и второго порядков. Выясняется, что алгебраическими поверхностями первого порядка являются лишь плоскости. определяются уравнениями вида:

  Ax ²+ By ²+ Cz ²+ Dxy+ Eyz + Fxz+ Gx+ Ну + Mz + N= 0.

 Основной метод исследования и классификации этих поверхностей заключается в подборе такой декартовой прямоугольной системы координат, в которой уравнение поверхности имеет наиболее простой вид, и последующем исследовании этого простого уравнения. Важнейшими вещественными поверхностями второго порядка являются ,однополостный и двуполостный гиперболоиды,эллиптический и гиперболический .Эти поверхности в специально выбранных декартовых прямоугольных системах координат имеют следующие уравнения:

  Перечисленные важнейшие поверхности второго порядка часто встречаются в различных вопросах механики, физики твёрдого тела, теоретической физике и инженерном деле. Так, при изучении напряжений, возникающих в твёрдом теле, пользуются понятием т. н: эллипсоид напряжений. В различных инженерных сооружениях применяются конструкции в форме гиперболоидов и параболоидов.

  Лит.:Декарт Р., Геометрия, [пер. с франц.], М.-Л., 1938; Вилейтнер Г., История математики от Декарта до середины XIX столетия, пер. с нем., 2 изд., М., 1966; Ефимов Н. В., Краткий курс аналитической геометрии, 9 изд., М., 1967; Ильин В. А., Позняк Э. Г., Аналитическая геометрия, М., 1967; Александров П. С., Лекции по аналитической геометрии, М., 1968; Бахвалов С. В., Моденов П. С., Пархоменко А. С., Сборник задач по аналитической геометрии, 3 изд., М., 1964; Клетеник Д. В., Сборник задач по аналитической геометрии, 9 изд., М., 1967.

  Э. Г. Позняк.

Рис. 4. к ст. Аналитическая геометрия.

Рисунки 1, 2, 3 к ст. Аналитическая геометрия.

Аналитическая философия

Аналити'ческая филосо'фия,направление современной буржуазной, главным образом англо-американской, философии, которое сводит философию к анализу языковых и понятийных (рассматриваемых в конечном счёте обычно так же, как языковые) средств познания.

  При этом философско-гносеологический анализ средств познания, характерный для классической философии и связанный с коренными проблемами соотношения субъекта и объекта, подменяется, как правило, исследованием частно-научных проблем: логических, логико-лингвистических, семиотических и пр. В рамках этих исследований представители А. ф. имеют определённые достижения в изучении особенностей языковых средств философии, возможностей логической формализации фрагментов «естественного» языка, логико-семантическом анализе философских понятий и пр. В то же время понимаемый т. о. анализ сторонники А. ф. противопоставляют философии как исследованию коренных мировоззренческих проблем, третируя последнее, как лишённую научно-познавательного значения «метафизику». Тем самым А. ф. продолжает линию в современной философии. Внутри современной А. ф. можно выделить два направления: ,которая в качестве средства анализа применяет аппарат современной математической логики, и ,отвергающую логическую формализацию как основной метод анализа и занимающуюся исследованием типов употребления выражений в естественном, обыденном языке, в том числе, когда он применяется при формулировке философских понятий. К первому направлению относятся логический эмпиризм (Р. ,Г. Фейгль, К. Гемпель, Ф. Франк) - непосредственное продолжение австро-немецкого логического позитивизма на американской почве, и т. н. логический прагматизм (У. Куайн, Н. Гудмен и др.). Философия лингвистического анализа (Г. Райл, Дж. Остин, П. Строусон, Дж. Уисдом) получила преобладающее влияние в Великобритании. Единые в своих претензиях на совершение позитивистской «революции в философии» оба эти течения выражают, однако, различные умонастроения: в то время как философия логического анализа считает себя философией науки и представляет линию т. н. сциентизма (от лат. scientia - наука) в современной буржуазной философии, сторонники философии лингвистического анализа выступают против какого-либо культа научного знания и оказываются адептами «естественного» отношения к миру, выраженного в обыденном языке.

  Понятие анализа, принятое в А. ф., появляется в буржуазной философии 20 в. в работах Б. и Дж. как определённый метод разработки философской проблематики в противоположность спекулятивному системосозиданию, характерному, в частности, для абсолютного идеализма Ф. и Б. . По существу, исходные установки и основные направления А. ф. сложились уже в довоенном неопозитивизме, в частности в логическом позитивизме Венского кружка и у английских философов 20-30-х гг. - последователей Мура и позднего Л. .Однако сам термин «А. ф.» получает распространение только после 2-й мировой войны, охватывая различные неопозитивистские течения буржуазной философии, предметом анализа которых были языковые средства. Распространение термина «А. ф.», вытесняющего термин «неопозитивизм», связано в основном с неудачами реализации программы неопозитивизма ещё на ранних его стадиях: с невозможностью упразднить классическую философскую проблематику, осуществить всеохватывающий анализ «языка науки» на основе неопозитивистских принципов, полностью «деидеологизировать» философию и пр. Для А. ф. как современного этапа эволюции неопозитивизма характерна тенденция, сохранив идею анализа как «антиметафизики», максимально освободиться от каких-либо содержательных предпосылок философского характера, в том числе от жёстких гносеологических постулатов раннего неопозитивизма (например, принципа рассматривать анализ как чистую технику и не ограничивать его какими-либо предвзятыми формами, связанными с определёнными концепциями знания. Тем самым современная А. ф. приходит либо к полной ликвидации себя как философии, при подмене философского исследования конкретным логико-лингвистическим, логико-семантическим и пр. анализом, либо к возвращению в завуалированной форме к проблемам философского характера. При этом для современной А. ф. характерны стремления сочетать элементы различных вариантов анализа и соединять анализ с концепциями и др., которые традиционно считались антитезой современного позитивизма.

  Лит.:Бегиашвили А. Ф., Метод анализа в современной буржуазной философии, Тб., 1960; Геллнер Э., Слова и вещи, пер. [с англ.], М., 1962; Богомолов А. С., Англо-американская буржуазная философия эпохи империализма, М., 1964, гл. 9, 10; Хилл Т. И., Современные теории познания, пер. с англ., М., 1965, ч. 5; Современная идеалистическая гносеология, М., 1968; Pap A., Elements of analytic philosophy, N. Y., 1949; The revolution in philosophy, with an introduction by G. Ryle, L., 1956; Uгмson J. 0., Philosophical analysis, Oxf., 1956; Classics of analytic philosophy, ed. by R. Ammerman, N. Y., 1965.

  В. С. Швырев.

Аналитическая химия

Аналити'ческая хи'мия,наука о методах изучения состава вещества. Она состоит из двух основных разделов: качественного анализа и количественного анализа. совокупность методов установления качественного химического состава тел - идентификации атомов, ионов, молекул, входящих в состав анализируемого вещества. Важнейшими характеристиками каждого метода качественного анализа являются: специфичность и чувствительность. Специфичность характеризует возможность обнаружения искомого элемента в присутствии других элементов, например железа в присутствии никеля, марганца, хрома, ванадия, кремния и др. Чувствительность определяет наименьшее количество элемента, которое может быть обнаружено данным методом; чувствительность выражается для современных методов значениями порядка 1 мкг(одной миллионной доли грамма).

  Количественный анализ - совокупность методов определения количественного состава тел, т. е. количественных соотношений, в которых находятся химические элементы или отдельные соединения в анализируемом веществе. Важнейшей характеристикой каждого метода количественного анализа является, наряду со специфичностью и чувствительностью, точность. Точность анализа выражается значением относительной ошибки, которая не должна в большинстве случаев превышать 1-2%. Чувствительность в количественном анализе выражают в процентах.

  Многие современные методы обладают весьма высокой чувствительностью. Так, методом радиоактивационного анализа можно установить наличие меди в кремнии с точностью до 2ґ10 ^-8%.

  В силу некоторых специфических особенностей в А. х. принято выделять анализ органических веществ (см. ниже).

  Особое место в А. х. занимает основывающийся на всей совокупности методов качественного и количественного, неорганического и органического анализа в приложении их к тому или иному конкретному объекту. Технический анализ включает аналитический контроль процессов производства, сырья, готовой продукции, воды, воздуха, отходящих газов и т. д. Особенно велика потребность в «экспрессных» методах технического анализа, требующих 5-15 мин.для отдельного определения.

  Определение пригодности того или иного продукта для нужд человека имеет столь же древнюю историю, как и само его производство. Первоначально такое определение имело целью установление причин несоответствия получаемых свойств продуктов желаемым или необходимым. Это относилось к продуктам питания - таким, как хлеб, пиво, вино и др., для испытания которых использовались вкус, запах, цвет (эти методы испытания, называемые органолептическими, применяются и в современной пищевой промышленности). Сырьё и продукты древней металлургии - руды, металлы и сплавы, которые применяли для изготовления орудий производства (медь, бронза, железо) или для украшения и товарообмена (золото, серебро), испытывались по их плотности, механическим свойствам посредством пробных плавок. Совокупностью подобных методов испытания благородных сплавов пользуются и до сих пор в пробирном анализе. Определялась доброкачественность красителей, керамических изделий, мыла, кожи, тканей, стекла, лекарственных препаратов. В процессе такого анализа стали различаться отдельные металлы (золото, серебро, медь, олово, железо), щёлочи, кислоты.

  Методы А. х. имели исключительное значение в установлении основных законов химии (см. , ) уточнении понятия о химическом элементе и др.

  В алхимический период развития химии (см. ), характеризовавшийся развитием экспериментальных работ, увеличилось число различаемых металлов, кислот, щелочей, возникло понятие о соли, сере как горючем веществе и т. д. В этот же период были изобретены многие приборы для химических исследований, применено взвешивание исследуемых и используемых веществ (14-16 вв.).

  Главное же значение алхимического периода для будущего А. х. заключалось в том, что были открыты чисто химические методы различения отдельных веществ; так, в 13 в. было обнаружено, что «крепкая водка» (азотная кислота) растворяет серебро, но не растворяет золото, а «царская водка» (смесь азотной и соляной кислот) растворяет и золото. Алхимики положили начало химическим определениям; до этого для различения веществ пользовались их физическими свойствами.