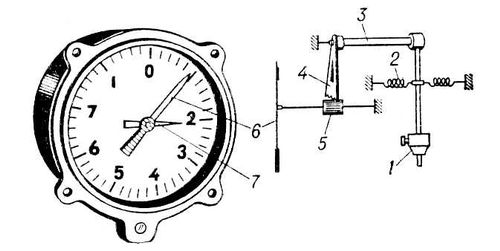
Аксельбант

Аксельба'нт(нем. Achselband, от Achsel - плечо и Band - лента, тесьма), оплечье или наплечье, плетёный шнур (золотой, серебряный или цветной нитяной) с металлическими наконечниками, пристёгиваемый к правому (реже левому) плечу. В дореволюционной русской армии А. был принадлежностью формы генералов, офицеров Генерального штаба и адъютантов всех родов войск. В настоящее время А. носят в некоторых иностранных армиях.

Аксельрод Джулиус

А'ксельрод(Axelrod) Джулиус (р. 30.5.1912, Нью-Йорк), американский физиолог и фармаколог, член Национальной АН США (1971). Окончил университет в Нью-Йорке (1935). Доктор философии. В 1933-49 работал в университете в Нью-Йорке. С 1949 в Национальном институте здоровья (Бетесда, штат Мэриленд), где с 1955 руководит отделом фармакологии Института психической гигиены. Основные труды по обмену норадреналина. Выявил основные пути его инактивации. Исследовал роль нарушений обмена катехоламинов в патогенезе гипертонии и некоторых заболеваний нервной системы. Нобелевская премия (1970, совместно с Б. Кацем и У. Эйлером ) .

 Соч.: Metabolism ofepinephrine and other sympathomimetic amines, «Physiological Review», 1959, v. 39; Methylation reactions in the formation and metabolism of catecholamines and other biogenic amines, «Pharmacological Reviews», 1966, v. 18.

Аксельрод Любовь Исааковна

Аксельро'д(псевдоним - Ортодокс) Любовь Исааковна (1868 - 5.2.1946), русский философ и литературовед. С 1884 в революционном движении. В 1887-1906 жила в эмиграции, где в 1892 вошла в марксистскую группу «Освобождение груда». В 1900 окончила Бернский университет. Вслед за Г. В. Плехановым А. защищала материалистическое понимание истории, выступала против «экономизма» , теории познания неокантианства (сборник «Философские очерки. Ответ философским критикам исторического материализма», 1906), эмпириокритицизма (сборник «Против идеализма. Критика некоторых идеалистических течений философской мысли», 1922). При изложении марксистской философии А. делала уступки агностицизму и релятивизму,допускала ошибки в духе теории иероглифов; выступала с критикой книги В. И. Ленина «Материализм и эмпириокритицизм» . В 1903 примкнула к меньшевикам. В 1917 А. член меньшевистского ЦК, член плехановской группы «Единство». В 1921-23 преподавала в институте красной профессуры, позднее работала в институте научной философии России, ассоциации научно-исследовательских институтов АН СССР (РАНИОН) и в Государственной академии художественных наук.

  В 20-х .гг. А. - представитель группы «механистов» . В последние годы жизни занималась социологическими проблемами искусства.

  Соч.: Карл Маркс как философ, X., 1924; Критика основ бурж. обществоведения и материалистическое понимание истории, вып. 1, Иваново-Вознесенск, 1924; Этюды и воспоминания, Л., 1925; Лев Толстой, 2 изд., [М.], 1928; Идеалистическая диалектика Гегеля и материалистическая диалектика Маркса, М. - Л., 1934.

  Лит.:Ленин В. И., Полн. собр. соч., 5 изд., т. 18, с. 341 - 44; т. 26, с. 88 - 89; т. 46, с. 321 - 22; Любовь Исааковна Аксельрод. К XXV-летию научно-литературной деятельности, М., 1926 (имеется библ.); Асмус В. Ф., Л. И. Аксельрод и философия, «Под знаменем марксизма», 1928, № 9 - 10; Деборин А., Ревизионизм под маской ортодоксии, там же, 1927, № 9 и 12; 1928, № 1; История философии, т. 6, кн. 1, М.,1965, с. 78, 141, 417, 437, 440.

Аксельрод Павел Борисович

Аксельро'дПавел Борисович (1850 - 1928, Берлин), один из лидеров меньшевиков. Учился в Киевском университете. В 70-е гг. - народник (вначале бакунист, а с расколом в 1879 «Земли и воли» - чернопеределец). С 1883 член марксистской группы «Освобождение труда». С 1900 один из редакторов «Искры» и «Зари». В 1883 - 1903, пропагандируя марксизм, написал ряд работ, в которых проявилась идеализация буржуазной демократии и парламентской деятельности западноевропейских. социал-демократических партий. Со 2-го съезда РСДРП(1903) один из идеологов меньшевизма, враг большевиков. В 1905 выдвинул антимарксистскую идею т. н. «рабочего съезда». На 4-м Объединительном съезде РСДРП (1906) выступил с оппортунистической идеей политического сотрудничества пролетариата с буржуазией. В годы реакции идейный вождь ликвидаторов;во время 1-й мировой войны - социал-шовинист. В 1917 член исполкома Петроградского совета, активно поддерживал буржуазное Временное правительство. После Октябрьской революции - эмигрант. Один из лидеров 2-го Интернационала, сторонник реформизма, противник Советской власти, вплоть до призыва к вооруженной интервенции.

Аксель-Хейберг

А'ксель-Хе'йберг(Axel Heiberg), остров на С. Канадского Арктического архипелага. Отделен от Земли Элсмир узкими проливами Юрика и Нансен. Площадь 34,4 тыс. км ^2.Поверхность образуют горные хребты высотой до 2000 м,покрытые крупными ледниковыми куполами высотой до 2134 м.Берега постоянно блокированы льдами и труднодоступны. Открыт в 1899 норвежцем О. Свердрупом.

Аксенёнок Георгий Александрович

АксенёнокГеоргий Александрович (р. 18.11.1910, Полоцк), советский юрист, член-корреспондент АН СССР (1966), специалист в области земельного и колхозного права. Член КПСС с 1930. Государственный советник юстиции 3-го класса. Заведующий сектором института государства и права АН СССР (с 1955). Основные труды: «Право государственной собственности на землю в СССР» (1950), «Земельные правоотношения в СССР» (1958), «Правовое положение колхозов в СССР» (1963). Награжден 2 орденами.

Аксёнов Василий Павлович

АксёновВасилий Павлович (р. 20.8.1932, Казань), русский советский писатель. В 1956 окончил Ленинградский медицинский институт. Первые рассказы опубликовал в 1959. Основная тема А. - жизнь современной молодёжи: повесть «Коллеги» (1960; одноименная пьеса совместно с Ю. Стабовым, 1961; одноименный фильм, 1963), романы «Звёздный билет» (1961), «Пора, мой друг, пора» (1964), повесть «Апельсины из Марокко» (1963), сборники «Катапульта» (1964), «На полпути к Луне» (1966), пьеса «Всегда в продаже» (постановка театра «Современник», 1965); в 1968 опубликована сатирико-фантастическая повесть «Затоваренная бочкотара». Многие его произведения справедливо критиковались в печати за известную односторонность в изображении современной молодёжи, злоупотребление «жаргонизмами».

  Лит.:Рассадин Ст., Шестидесятники, «Юность», 1960, № 12; его же, Шестеро в кузове, не считая бочкотары, «Вопросы литературы», 1968, № 10; Белаш Ю., На Сашу Зеленина они не похожи, «Молодая Гвардия», 1961, № 4; Гейдеко В., Перед следующим шагом, «Лит. газета», 1964, 6 июня.

Аксёнов Владимир Викторович

АксёновВладимир Викторович (р. 1.2.1935, с. Гиблицы Касимовского района Рязанской области), лётчик-космонавт СССР, Герой Советского Союза (1976). Член КПСС с 1959. В 1953 окончил машиностроительный техникум. Учился в военно-авиационной школе и Чугуевском военно-авиационном училище. С 1957 работал в КБ. В 1963 окончил Всесоюзный заочный политехнический институт. С 1973 в отряде космонавтов. 15-23 сентября 1976 совершил (совместно с В. Ф. Быковским ) полёт на космическом корабле «Союз-22» в качестве бортинженера. Время полёта 7 сут21 ч54 мин.Награжден орденом Ленина и медалями.

Аксёново

Аксёново,кумысолечебный курорт и ж.-д. станция в Башкирской АССР. В 10 кмот ж.-д. станции санаторий им. А. П. Чехова для больных лёгочным туберкулёзом, функционирующий круглый год. Климат континентальный: сухое жаркое лето и устойчивая морозная зима.

Аксёново-Зиловское

Аксёново-Зи'ловское,посёлок городского типа в Чернышевском районе Читинской области РСФСР. Расположен на р. Белый Урюм (бассейн Амура). Ж.-д. станция (Зилово) на Сибирской магистрали. 8 тыс. жителей (1968). Возник в 1908 в связи с постройкой железной дороги. Предприятия железнодорожного транспорта.

Аксенфельд Израиль

Аксенфе'льдИзраиль (1787, Немиров Подольской губернии, - 1866, Париж), еврейский писатель. Писал на идиш. Был нотариусом. Уехал за границу. Творчество А. проникнуто идеями просветительства. Автор романов, драм и рассказов, большинство которых не было опубликовано и, вероятно, погибло. Опубликовал пьесы «Первый еврейский рекрут» (1862), «Муж и жена, сестра и брат» (1867), «Обманутый мир» (1870), «От богатства к нищете» (1870), повесть «Головной убор» (1861).

  Соч.: Верк. Унтер дер редакцие фун М. Винер, X. - К., 1931.

  Лит.:Рейзен З., Фун Мендельсон биз Менделе, Варшава, 1923; Ойслендер Н., Ди элтере йидише драме ун ир кинстлерише ойсшатунг. К., 1927.

Аксер Эрвин

А'ксер(Axer) Эрвин(р. 1.1.1917, Вена), польский режиссёр. По окончании Государственного института театрального искусства в Варшаве работал в 1939-41 в театрах Львова, Лодзи. С 1946 режиссёр «Театра Вспулчесны» в Варшаве (до 1949 театр назывался «Камеральны»; в 1955-57 одновременно возглавлял «Театр Народовы», Варшава). Особое внимание уделяет постановкам современной польской драматургии: «Немцы» (1949) и «Первый день свободы» (1959) Кручковского, «Обыкновенное дело» Тарна (1951), «Тревожное дежурство» Лютовского (1955), «Два театра» Шанявского (1968) и др. Ставит также зарубежную драматургию: «Бидерман и поджигатели» Фриша (1959), «Карьера Артуро Уи» Брехта (1962; 1963, Большой драматический театр им. Горького, Ленинград) и др. Присущий А. публицистический темперамент раскрывается в формах интеллектуального театра. С 1947 преподаёт в польских театральных школах (Лодзь, Варшава). Выступает с теоретическими статьями в журнале «Театр» («Teatr»), пишет фельетоны о театре. Государственная премия ПНР (1962; за спектакли «Ифигения в Тавриде» Гёте и «Карьера Артуро Уи»).

  Соч.: Pare uwag о inscenizacji, «W pew-nym miescie», «Teatr», 1950, № 2 - 4; Listy ze sceny, ser. I - 2, Warsz., 1955 - 57.

Аксерофтол

Аксерофто'л,то же, что витамин A ₁. См. Витамины .

Аксессуар

Аксессуа'р(франц. accessoire),

  1) принадлежность чего-либо; сопутствующий чему-либо предмет (например, А. в одежде, придающие костюму законченность: шарф, перчатки, сумка, галстук и др.).

  2) В театре - предметы бутафории или реквизита .

 3) В изобразительном искусстве - второстепенные, вспомогательные детали изображения.

Аксиальный вектор

Аксиа'льный ве'ктор(от лат. axis - ось), то же, что осевой вектор .

Аксинит

Аксини'т(от греч. axнn - топор; по форме кристаллов), минерал, алюмоборосиликат кальция, железа, марганца. По соотношению Fe ²⁺и Mn2 ⁺различают ферроаксинит, севергенит и мангансевергенит. Кристаллизуется в триклинной системе. Обычно образует широкие кристаллы с острыми концами. Твердость по минералогической шкале 6,5-7; плотность 3250-3300 кг/м ³.Цвет большей частью бурый, часто с синеватым или фиолетовым оттенком. Нередко встречается в тесной связи с рудами железа, меди, полиметаллов, олова и марганца. С различными минеральными парагенезисами ассоциируют А. соответствующих составов. Так, марганцовистые А. сопровождают оловянное и полиметаллическое оруденение, а железистые А. характерны для месторождений меди и железа.

Аксиология

Аксиоло'гия,см. Ценностей теория .

Аксиома

Аксио'ма(греч. axнMma - удостоенное, принятое положение, от axiуM - считаю достойным), положение некоторой данной теории, которое при дедуктивном построении этой теории не доказывается в ней, а принимается за исходное, отправное, лежащее в основе доказательств других предложений этой теории. Обычно в качестве А. выбирают такие предложения рассматриваемой теории, которые являются заведомо истинными или могут в рамках этой теории считаться истинными.

  Возникнув в Древней Греции, термин «А.» впервые встречается у Аристотеля, а затем через труды последователей и комментаторов Евклида прочно входит в геометрию. В средние века господство аристотелевской философии обусловило его проникновение в другие области науки, а через неё и в обыденную жизнь. А. стали называть такое общее положение, которое, будучи совершенно очевидным, не нуждается в доказательстве. Природу этой очевидности видели, следуя взглядам, идущим ещё от Платона, в прирождённости человеку таких основных истин, как математическая А. Учение И. Канта об априорности последних, т. е. о том, что они предшествуют всякому опыту и не зависят от него, было кульминацией таких взглядов на А. Первым крупным ударом по взгляду на А. как на вечные и непреложные «априорные» истины явилось построение Н. И. Лобачевским неевклидовой геометрии.

  Критикуя взгляды Гегеля на логическую А. (на фигуры аристотелевских силлогизмов), В. И. Ленин писал: «...практическая деятельность человека миллиарды раз должна была приводить сознание человека к повторению разных логических фигур, дабы эти фигуры могли получить значение аксиом» («Философские тетради», 1969, с. 172). Именно в обусловленности многовековым человеческим опытом, практикой, включая сюда также и эксперимент, и опыт развития науки,- причина очевидности А., рассматриваемых как истины, не нуждающиеся в доказательстве.

  Вместе с тем крушение взгляда на А. как на «априорные» истины привело к раздвоению понятия А. Всё возрастающая в связи с запросами практики необходимость экспериментировать в области построения новых теорий, заменять одну А. другой, а также их относительность, зависимость от ранее встречающихся конкретных условий опыта и уровня развития науки, приводящая к невозможности выбрать раз навсегда и навечно в качестве А. такие положения, которые будут истинны абсолютно во всех условиях, - всё это обусловило появление понятия А. в смысле, несколько отличном от традиционного. Понятие А. в этом смысле зависит от того, построение какой теории рассматривается и как оно проводится. А. данной теории при этом называются просто те предложения этой теории, которые при данном построении её как дедуктивной теории принимаются за исходные, притом совершенно независимо от того, сколь они просты и очевидны. Более того, уже из опыта, например, построения различных неевклидовых геометрий и их последующего истолкования и практического использования стала ясной невозможность при построении (или аксиоматизации) той или иной теории каждый раз требовать заранее истинности её А.

  С созданием развитого аппарата математической логики связано дальнейшее развитие понятия А. В формальном исчислении А. является уже не предположением некоторой содержательной научной теории, а просто одной из тех формул, из которых по правилам вывода этого исчисления выводятся остальные доказуемые в нём формулы («теоремы» этого исчисления). См. также Аксиоматический метод и литературу при этой статье.

  А.В. Кузнецов.

Аксиоматическая теория множеств

Аксиомати'ческая тео'рия мно'жеств,формулировка множеств теории в виде формальной (аксиоматической) системы (см. Аксиоматический метод ) .Основным побудительным стимулом для построения А. т. м. явилось открытие в «наивной» теории множеств Г. Кантора.предназначенной для обоснования классической математики, парадоксов (антиномий), т. е. противоречий. Все эти парадоксы (например, парадокс Кантора, связанный с рассмотрением «множества всех множеств», или парадокс Рассела, в котором рассматривается «множество всех множеств, не содержащих самих себя в качестве элемента») обусловлены неограниченным применением в канторовой теории множеств т. н. принципа свёртывания (или абстракции), согласно которому для всякого свойства существует множество, состоящее из всех предметов, обладающих этим свойством (этот принцип фактически содержится уже в первой фразе всех традиционных изложений теории множеств: «мы будем рассматривать произвольные множества элементов произвольной природы» и т.п.).

  В первой из известных систем А. т. м. - системе Цермело - Френкеля, или ZF(сформулирована в 1908 Э. Цермело,пополнена в 1921 - 22 и позже А. Френкелем), принцип свёртывания заменяется несколькими его частными случаями: аксиомой существования пары {х,у}любых (данных) множеств хи у,аксиомой существования объединения всех элементов произвольного множества хв новое множество S( x), аксиомой существования множества Р( х) всех частей произвольного множества х,аксиомой существования бесконечного множества и т.н. схемами аксиом выделения (согласно которой для всякого множества хи свойства р существует множество элементов х,обладающих свойством j) и подстановки (утверждающей, что для любого взаимно однозначного отображения элементов множества х,описываемого на языке системы ZF,существует множество таких z,на которые отображаются эти элементы х) .Не подпадает под схему принципа свёртывания т. н. аксиома выбора (о существовании «множества представителей», т. е. множества содержащего в точности по одному элементу из каждого из данных непустых попарно непересекающихся множеств). Как и во всякой другой системе А. т. м., в ZFпостулируется также аксиома объёмности (экстенсиональности), согласно которой множества, состоящие из одних и тех же элементов, совпадают. Иногда к ZFприсоединяют некоторые др. аксиомы более специального назначения. Формулы ZFполучаются из «элементарных формул» вида хО у(« xпринадлежит y») средствами исчисления предикатов.

  Позднее были построены многочисленные видоизменения ZFи систем, отличающихся от ZFтем, что «плохие» (приводящие к парадоксам) совокупности элементов не вовсе исключаются из рассмотрения, а признаются «собственно классами», т. е. множествами, не могущими принадлежать в качестве элемента другим множествам (эта идея, идущая от Дж . Неймана,была затем развита швейцарским математиком П. Бернайсом, К. Гёделем и др.). Системы эти, в отличие от ZF,могут быть заданы посредством конечного числа аксиом.

  Другой подход к А. т. м. воплощён в теории типов Б. Рассела и А. Н. Уайтхеда (Англия, 1910-13) и её различных модификациях, в которых на аксиому свёртывания не накладывают типичных для ZFи др. систем ограничений, но реформируют сам язык теории: вместо одного алфавита переменных х, у,z... вводится бесконечная последовательность алфавитов: x ₁, y ₁, z ₁,...; x ₂, y ₂, z ₂,...;...; x _n, y _n, z _n,...;... различных «типов» n,а элементарные формулы имеют вид x _nО y _n+1или

  x _n= y _n .Теории типов строятся на основе исчисления предикатов с различными видами переменных [а при естественной замене символики x _nО y _n+1на y _n+1( x _n) и x _n= y _nна x _n~ y _nсами могут рассматриваться как системы расширенного исчисления предикатов, а не теории множеств]. В системе NF(New Foundation), введённой в 1937 американским математиком У. в. О. Куайном, комбинируются оба упомянутых подхода: язык NF -тот же, что в ZF,а аксиомы свёртывания должны получаться из аксиом теории типов удалением индексов при переменных.

  Для различных систем А. т. м. и отдельных их аксиом рассматривался вопрос об их (относительной) непротиворечивости.В 1940 К. Гёдель доказал относительную непротиворечивость аксиомы выбора и континуум-гипотезы (см. Континуума проблема ) для описанной им системы е и ZF;в дальнейшем этот результат был перенесён на теорию типов (самую слабую из перечисленных систем), а затем и на NF(в соответствующей форме). В 1963 американский математик П. Дж. Коэн доказал для ZF(а тем самым и для е ) относительную непротиворечивость отрицания континуум-гипотезы, в т. ч. и в случае, если к ZFприсоединена аксиома выбора. Он же доказал, что к ZFможно присоединить без возникновения противоречия аксиому о том, что континуум не может быть вполне упорядочен (из этой аксиомы сразу следует отрицание аксиомы выбора).

  Упомянутых ограничений на принцип свёртывания (или на язык системы) достаточно, чтобы в А. т. м. не возникал ни один из известных парадоксов. Однако проблема абсолютной непротиворечивости, ввиду теоремы Гёделя о неполноте (см. Метатеория ) ,требует привлечения существенно новых идей. В частности, полученное в 1960 доказательство непротиворечивости ZF(и теории типов, но не NF) потребовало привлечения средств т. н. ультраинтуиционизма.

  Лит.:Гёдель К., Совместимость аксиомы выбора и обобщённой континуум-гипотезы с аксиомами теории множеств, пер. с англ., «Успехи математических наук», 1948, т. 3, в. 1; Есенин-Вольпин А. С., К обоснованию теории множеств, в сборнике: Применение логики в науке и технике, [М., I960], с. 22 - 118; Френкель А. А. и Бар-Хиллел И., Основания теории множеств, пер. с англ., М., 1966 (библ.); Коэн П. Дж., Теория множеств и континуум-гипотеза, пер. с англ., М., 1969; Quine W. О. van, Set theory and its logic, Camb., 1963.

  Ю. А. Гастев, А. С. Есенин-Вольпин.

Аксиоматический метод

Аксиомати'ческий ме'тод,способ построения научной теории, при котором в её основу кладутся некоторые исходные положения (суждения) - аксиомы,или постулаты,из которых все остальные утверждения этой науки ( теоремы ) должны выводиться чисто логическим путём, посредством доказательств.Назначение А. м. состоит в ограничении произвола при принятии научных суждений в качестве истин данной теории. Построение науки на основе А. м. обычно называется дедуктивным. Все понятия дедуктивной теории (кроме фиксированного числа первоначальных) вводятся посредством определений,выражающих (или разъясняющих) их через ранее введённые понятия. В той или иной мере дедуктивные доказательства, характерные для А. м., применяются во многих науках. Но, несмотря на попытки систематического применения А. м. к изложению философии (Б. Спиноза), социологии (Дж. Вико), политической экономии (К. Родбертус-Ягецов), биологии (Дж. Вуджер) и др. наук, главной областью его приложения до сих пор остаются математика и символическая логика, а также некоторые разделы физики (механика, термодинамика, электродинамика и др.).

  А. м прошёл в своём историческом развитии 3 стадии. Первая связана с построением геометрии в Древней Греции. Основное сочинение этого периода - «Начала» Евклида (хотя, по-видимому, и до него Пифагор,которому приписывается открытие А. м., а затем Платон и его ученики немало сделали для развития геометрии на основе А. м.). В то время считалось, что в качестве аксиом должны выбираться суждения, истинность которых «самоочевидна», так что истинность теорем считалась гарантированной безупречностью самой логики. Но Евклиду не удалось ограничиться чисто логическими средствами при построении геометрии на основе аксиом. Он охотно прибегал к интуиции в вопросах, касающихся непрерывности, взаимного расположения и равенства геометрических объектов. Впрочем, во времена Евклида такие обращения к интуиции могли и не восприниматься как выход за пределы логики - прежде всего потому, что сама логика не была ещё аксиоматизирована (хотя частичная формализация логики, осуществленная Аристотелем и его последователями, и была некоторым приближением к аксиоматизации). Не было и достаточной отчётливости во введении первоначальных понятий и при определении новых понятий.

  Начало второй стадии в истории А. м. связывают обычно с открытием Н. И. Лобачевским , Я. Больяйи К. Ф. Гауссом возможности построить непротиворечивым образом геометрию, исходя из систем аксиом, отличной от евклидовой. Это открытие разрушило убеждение в абсолютной («очевидной» или «априорной») истинности аксиом и основанных на них научных теорий. Теперь аксиомы стали пониматься просто как исходные положения данной теории, вопрос же об их истинности в том или ином смысле (и выбор в качестве аксиом) выходит за рамки аксиоматической теории как таковой и относится к её взаимоотношению с фактами, лежащими вне её. Появилось много (и притом различных) геометрических, арифметических и алгебраических теорий, которые строились средствами А. м. (работы Р. Дедекинда,Г. Грасмана и др.). Эта стадия развития А. м. завершилась созданием аксиоматических систем арифметики (Дж. Пеано , 1891), геометрии (Д. Гильберт,1899), исчисления высказываний и предикатов (А. Н. Уайтхед и Б. Рассел, Англия, 1910) и аксиоматической теории множеств (Э. Цермело,1908).

  Гильбертовская аксиоматизация геометрии позволила Ф. Клейну и А. Пуанкаре доказать непротиворечивость геометрии Лобачевского относительно евклидовой геометрии посредством указания интерпретации понятий и предложений неевклидовой геометрии в терминах геометрии Евклида, или, как говорят, построения модели первой средствами второй. Метод моделей (интерпретаций) стал с тех пор важнейшим методом установления относительной непротиворечивости аксиоматических теорий. В то же время со всей отчётливостью выявилось, что, кроме «естественной» интерпретации (т. е. той, ради уточнения и развития которой данная теория строилась), у аксиоматической теории могут быть и др. интерпретации, причём её можно с равным основанием считать «говорящей» о каждой из них.

  Последовательное развитие этой идеи и стремление точно описать логические средства вывода теорем из аксиом привели Гильберта к концепции формального А. м., характерной для третьей, современной его стадии. Основная идея Гильберта - полная формализация языка науки, при которой её суждения рассматриваются просто как последовательности знаков (формулы), не имеющие как таковые никакого смысла (который они приобретают лишь при некоторой конкретной интерпретации). Это относится и к аксиомам - как общелогическим, так и специфическим для данной теории. Для вывода теорем из аксиом (и вообще одних формул из других) формулируются специальные правила вывода (например, т. н. правило modus ponens - «правило зачёркивания», позволяющее получить Виз Аи «А влечёт В»). Доказательство в такой теории ( исчислении,или формальной системе ) -это просто последовательность формул, каждая из которых либо есть аксиома, либо получается из предыдущих формул последовательности по какому-либо правилу вывода.