 |
|
Популярные авторы:: Горький Максим :: Азимов Айзек :: Чехов Антон Павлович :: БСЭ :: Раззаков Федор :: Лем Станислав :: Толстой Лев Николаевич :: Лондон Джек :: Желязны Роджер :: Борхес Хорхе Луис Популярные книги:: Сила момента сейчас :: Снежная страна :: Справочник по реестру Windows XP :: Дом страха :: Не соблазняй повесу :: Автобан нах Познань :: Бурый волк :: Число власти :: Свободные навсегда :: Роботы зари [Роботы утренней зари] |
Большая Советская Энциклопедия (ЧИ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ЧИ) - Чтение (стр. 9)
Вместе с изучением свойств целых чисел возникло и стало развиваться новое направление Ч. т., изучающее арифметику числовой прямой. Уже Л. Эйлер отмечал, что корни квадратные из целых чисел и логарифмы целых чисел принципиально отличаются друг от друга. Последнее обстоятельство обрело точную математическую формулировку после работ Ж. Лиувилля (1844), который ввёл понятия и .Оказывается, алгебраические числа «плохо» приближаются рациональными дробями. Ж. Лиувилль доказал, что если алгебраическое число является корнем уравнения степени n, то, приближаясь к нему дробями вида P/Q, где Ри Q- целые взаимно простые числа, подойти существенно ближе чем Q ¾ nк нему нельзя (теорема Лиувилля). Отсюда сразу следует существование бесконечного числа неалгебраич. чисел, которые стали называть трансцендентными. Например, таким будет число
Однако вопрос об алгебраичности и трансцендентности конкретных чисел труден, и первыми были такие вопросы о классических постоянных p и е. В конце 19 - начале 20 вв. Ч. т. продолжала развиваться по многим направлениям, причём для решения отдельных задач создавались общие методы, применимые к широкому кругу задач, иногда далеко удалённых от первоначальных. Часто созданные здесь методы и понятия дают толчок развитию новых направлений. Теория алгебраических чисел разделилась на два направления: одно изучает конкретные числа, доказывая их трансцендентность, другое изучает степень приближения алгебраических чисел рациональными или алгебраическими. В первом направлении общие методы были созданы Ш. (1873), доказавшим трансцендентность числа e, и немецким математиком Ф. Линдеманом (1882), доказавшим трансцендентность числа p и тем самым решившим задачу о .Во втором - А. (1909) был предложен метод, с помощью которого он доказал, что в неравенстве Лиувилля к алгебраическому числу нельзя подойти существенно ближе чем Q ¾ n/2 .Следствием этого явилась теорема Туэ о конечности числа решений в целых числах хи ууравнения a 0x n+ a 1x n ¾1y+... + a n ¾1xy n ¾1+ a ny n=А, где a 0, a 1, ..., a n, А -целые числа, n³ 3. Дальнейшее изучение простых чисел привело к новому методу в Ч. т., связанному с функцией x ( s). Б. доказал, что дзета-функцияx ( s) аналитически продолжается на всю плоскость комплексного переменного, является аналитической в каждой точке плоскости, за исключением s =1, где она имеет полюс первого порядка с вычетом, равным 1, удовлетворяет функциональному уравнению x( s)= x(1¾ s), где
Г ( s) -гамма-функция, и имеет бесконечно много нулей в полосе 0 Ј Re s= 1 (эти нули называют нетривиальными, а полосу - критической). Он установил тесную связь между нетривиальными нулями x ( s) и асимптотическим поведением p( х). Изучение асимптотической формулы для функции Чебышева
где L( n) = ln p, если n = р кL( n) =0, если n¹ p k, эквивалентно такой же задаче для функции p( х). Функция Y( х) может быть выражена через интеграл от производящей функции - xў( s)/ x( s):
Б. Риман высказал гипотезу, что все нетривиальные нули x ( s) лежат на прямой Re s = 1/ 2, из чего следует, что y(
x)=
x + O(
Из справедливости любой из последних формул следует гипотеза Римана. По аналогичной схеме были изучены L-ряды Дирихле. В 1896 Ш. и Ж. доказали, что x( s) ¹ 0 в области Re s³ 1, откуда следовала формула (асимптотический закон распределения простых чисел)
Кроме этого, Ш. Ла Валле Пуссен доказал, что x( s) ¹ 0 в области
и что
где си c 1- положительные постоянные. Такой же результат был получен им и для простых чисел в арифметических прогрессиях: если p( х, k, l) -число простых чисел вида kn +1, nЈ х, kи l-взаимно простые числа, то
Метод получения асимптотических формул для p( х), Y( х), p( х, k, l), названный методом комплексного интегрирования, нашёл многочисленные применения. Основой этого метода служит формула
Теория квадратичных форм, начатая работами Л. Эйлера, К. Гаусса, П. Дирихле, продолжала своё развитие в работах А. Н.
, Е. И.
и А. А.
.В частности, А. Н. Коркин и Е. И. Золотарёв доказали теорему: переменным любой положительной кватернарной квадратичной формы определителя
Dможно придать такие целые значения, что значение формы не будет превосходить величины
Исследования А. А. Маркова относились к изучению минимумов бинарных квадратичных форм положительного определителя и привели к целому ряду новых открытий. Проблемы целых точек в областях на плоскости получили своё дальнейшее развитие в трудах Г. Ф. , создавшего (1903) метод, с помощью которого доказано, что остаточный член в асимптотической формуле Дирихле для числа целых точек под гиперболой имеет порядок корня кубического из главного члена. Позднее (1906) метод Вороного был перенесён В. на проблему Гаусса целых точек в круге с тем же результатом. В это же время были предприняты попытки найти решения аддитивных проблем Ч. т. и, в частности, решить .В 1909 она была решена Д. . Второе, третье и четвёртое десятилетия 20 в. были исключительно богаты новыми идеями и методами в Ч. т. Г. , решая задачи, связанные с устойчивостью Солнечной системы, пришёл к понятию равномерного распределения дробных долей целочисленных функций: дробные доли действительнозначной функции F( x) равномерно распределены на [0,1) при х=1,2,3.,.., если число попаданий дробных долей F( x) на любой интервал из [0.1) пропорционально длине этого интервала. Он доказал, что для равномерности распределения дробных долей F( x) необходимо и достаточно выполнение соотношения:
при любом фиксированном ½ m½>0, и получил нетривиальные оценки ½ S( F)½ в случае, когда F( x) -многочлен, старший коэффициент которого есть иррациональное число. И. М. Виноградов, изучая распределение значений символа Лежандра на отрезках малой длины по сравнению с модулем, доказал (1914) неравенство
из которого следует, что квадратичных вычетов и невычетов на любом отрезке, длина которого чуть больше
Норвежским математиком В. Бруном доказаны (1919) теоремы, которые в определённом смысле приближались к проблеме простых близнецов и проблеме Эйлера. А именно, им доказана бесконечность числа пар u 1и u 2, таких, что u 1- u 2=2 и число простых делителей u 1и u 2не превосходит девяти; а также разрешимость уравнения u 1+ u 2=2 N, с теми же условиями на u 1и u 2 Г. и Дж. опубликовали (1922-23) серию мемуаров под общим названием «Partitio Numerorum», в которых развили общий метод решения аддитивных задач Ч. т., получивший впоследствии название «кругового». Этот метод (на примере решения проблемы Варинга) состоит в следующем: пусть [missing picture],
тогда
где I k( N) -число решений уравнений Варинга, которое находят по формуле
Г. Харди и Дж. Литлвуд изучали последний интеграл при R®1- 0. Окружность интегрирования определённым образом разбивается на «большие» и «малые» дуги (отчего и получил название метод), при этом интегралы по «большим» дугам дают главный член асимптотической формулы для I k( N), а по «малым» - остаточный. Т. о. получают асимптотическую формулу величины
где s( N) -некоторый «особый ряд»; s( N) ³ с > 0, d >0 и k³ ( n-2)2 n ¾1+ 5. С помощью этого метода Г. Харди и Дж. Литлвуд получили следующие результаты: дали новое решение проблемы Варинга, причём в форме более точной, чем это было у Д. Гильберта; дали условное решение проблемы Гольдбаха; сформулировали и выписали гипотетические формулы для количества решений большого числа уравнений с простыми числами. В начале 30-х гг. 20 в. И. М. Виноградовым был найден т. н. метод тригонометрических сумм, позволивший решить многие проблемы Ч. т. Так, занимаясь проблемой Варинга, И. М. Виноградов обнаружил (1929), что результат Харди - Литлвуда будет значительно проще, если вместо производящих рядов рассматривать тригонометрические суммы вида
где F( x) -действительная функция, и пользоваться соотношением
Тогда I k( N) в проблеме Варинга запишется так:
где
Далее интервал интегрирования [0,1] разбивается рациональными несократимыми дробями вида a/ b, 0 Ј а< bЈ t, t - параметр, зависящий от N, на подинтервалы подобные «большим» и «малым» дугам кругового метода. Интервалы, отвечающие дробям с малыми знаменателями, и сумма интегралов по ним дают главный член асимптотической формулы для I k( N) .Другие интервалы отвечают «малым» дугам; для них И. М. Виноградов оценивает ½ S(a)½ методом Вейля и получает остаточный член. К тригонометрическим суммам сводятся и др. задачи Ч. т.: распределение дробных долей функций, целые точки в областях на плоскости и в пространстве, порядок роста дзета-функции в критической полосе и др. Причём главным в таких задачах является вопрос о возможно более точной оценке модуля тригонометрической суммы. И. М. Виноградов предложил два метода оценок тригонометрических сумм. Первый метод (1934) дал возможность получить новые оценки сумм Вейля. Следствием этого явились современные оценки, выведена асимптотическая формула в проблеме Варинга при k³ 4 n 2ln n, доказано, что для разрешимости уравнения Варинга при N³ N 0( n) достаточно не более 3 nln n+ 11 nслагаемых, получен новый остаточный член в асимптотических формулах для p( x) и y( х) (И. М. Виноградов, 1957) порядка
получено решение проблемы Гильберта - Камке (К. К. , 1953). Второй метод Виноградова (1937) позволил оценить такие тригонометрические суммы, в которых суммирование ведётся по простым числам:
Это привело к доказательству асимптотической формулы для числа представлений нечётного числа суммой трёх простых, из которой следовало, что все достаточно большие нечётные числа являются суммой трёх простых. Тем самым была решена .Этот метод привёл к решению других общих задач Ч. т., например проблемы Варинга в простых числах, проблемы распределения квадратичных вычетов и невычетов в последовательностях вида р+ а, где рпринимает значения простых чисел. Развитие идей А. Туэ (построение вспомогательного многочлена с высокой кратностью корня) и Д. Пойа (США) (целая аналитическая функция, принимающая в целых положительных точках целые значения и растущая медленнее 2 g ½ S ½, g < 1, является многочленом) привело А. О. и нем. математика Т. Шнейдера (1934) к решению 7-й проблемы Гильберта, утверждающей трансцендентность чисел вида a b, a ¹0,1, b - алгебраическое число степени ³ 2. К. доказал ряд теорем о трансцендентности значений функций типа e x(т. н. Е-функции) в алгебраических точках. В алгебраической Ч. т. доказан ряд теорем, обобщающих теоремы теории целых чисел на целые числа алгебраических числовых полей; некоторые из них привели и к чисто арифметическим результатам, сюда, в частности, относится теория представлений чисел полными и неполными разложимыми формами (простейшей из таких задач является уравнение Пелля). Развита также теория решений сравнений от двух и более переменных, из которой, например, следует, что сравнение F( x, у) є 0 (mod р), где
F -абсолютно неприводимый многочлен, имеет
Начиная с конца 40-х гг. и по настоящее время (1978) в Ч. т. появилось много работ в самых различных направлениях. Исследования ведутся как в классических областях, так и в новых. Советскими математиками Б. Н. и Д. К. полностью исследовано диофантово уравнение x 3 - ау 3 =1 (1940). В теории дзета-функции Римана А. Сельберг (Норвегия, 1942) доказал, что конечная доля всех нулей z( s) лежит на критической прямой Re s = 1/ 2; Ю. В. доказал, что наименьшее простое число в арифметической прогрессии с разностью kне превосходит k c, с -постоянная, и разработал дисперсионный метод (1958-1961), с помощью которого вывел асимптотическую формулу для числа представлений натурального Nсуммой простого и двух квадратов (проблема Харди - Литлвуда); этим же методом он получил асимптотическую формулу для числа решений неопределённого уравнения вида р- а = ху, рЈ N, хуЈ N, а -фиксированное целое (проблема простых делителей Титчмарша). Метод тригонометрических сумм Виноградова получил дальнейшее развитие в работах самого И. М. Виноградова и его учеников. Безуспешные попытки доказать гипотезу Римана привели к ряду методов, которые обходят её и в то же время позволяют решить определённые задачи Ч. т., выводимые из этой гипотезы. Сюда относится проблема оценки разности p n+1- р п= D n, которая сведена к оценке числа нулей дзета-функции в прямоугольниках вида s Ј Re sЈ 1, s > 1/ 2, ½Im s½Ј Т.Из таких «плотностных» теорем и границы нулей x( s), полученной на основе метода Виноградова, следует, что p n+1- р п= О( р п 0,6). К подобного рода результатам пришли и в теории распределения простых чисел в арифметических прогрессиях и её применениях к аддитивным задачам с простыми числами. В теории трансцендентных чисел английский математик К. Рот (1955) усилил метод Туэ и доказал, что алгебраическое число не может быть приближено рациональной дробью P/Qсущественно точнее, чем Q ¾2 ¾ e, e>0 - произвольно мало; английский математик А. Бейкер (1966) получил оценку снизу линейной формы логарифмов алгебраических чисел, что привело к эффективному доказательству теоремы Туэ о конечности решений уравнения a 0x n+ a 1x n ¾1y+... + a n-1xy n-1+ а пу n= А (указываются границы этих решений) и к эффективному усилению теоремы Лиувилля о приближении алгебраических чисел рациональными дробями. Большое количество проблем Ч. т. ещё не решено (сюда относятся проблемы простых близнецов, бесконечности простых чисел вида n 2+ 1, целых точек в круге и под гиперболой, распределения нулей дзета-функции, трансцендентность чисел p+ еи постоянной Эйлера и мн. др.). Лит.:Виноградов И. М., Основы теории чисел, 8 изд., М., 1972; его же, Метод тригонометрических сумм в теории чисел, М., 1971; его же, Особые варианты метода тригонометрических сумм, М., 1976; Карацуба А. А., Основы аналитической теории чисел, М., 1975; Боревич З. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972; Дэвенпорт Г., Мультипликативная теория чисел, пер. с англ., М., 1971; Чандрасекхаран К., Введение в аналитическую теорию чисел, пер. с англ., М., 1974; Хассе Г., Лекции по теории чисел, пер. с нем., М., 1953; Дирихле П. Г. Л., Лекции по теории чисел, пер. с нем., М.-Л., 1936; Титчмарш Е. К., Теория дзета-функции Римана, пер. с англ., М., 1953; Венков Б. А., Элементарная теория чисел, М.-Л., 1937. А. А. Карацуба. Числа заполнения Чи'сла заполне'нияв квантовой механике и квантовой статистике, числа, указывающие степень заполнения квантовых состояний частицами квантово-механической системы многих .Для системы частиц с полуцелым (фермионов) Ч. з. могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых, для системы частиц с целым спином (бозонов) - любые целые числа: 0, 1, 2,... Сумма всех Ч. з. должна быть равна числу частиц системы. С помощью Ч. з. можно описывать и числа элементарных возбуждений ( ) квантовых полей; в этом случае их сумма не фиксирована. Средние по статистически равновесному состоянию Ч. з. для идеальных квантовых газов определяются функциями распределения Ферми - Дирака и Бозе - Эйнштейна [см. , формула (19)]. Понятие Ч. з. лежит в основе метода , который называется также «представлением Ч. з.». Д. Н. Зубарев. Численное решение уравнений
Чи'сленное реше'ние уравне'ний,нахождение приближённых решений алгебраических и трансцендентных уравнений. Ч. р. у. сводится к выполнению арифметических операций над коэффициентами уравнений и значениями входящих в него функций и позволяет найти решения уравнений с любой наперёд заданной точностью. К Ч. р. у. сводятся многие задачи математики и её приложений. Хотя общие методы Ч. р. у. появились лишь в 17 в. (И.
), но ещё
(начало 13 в.) вычислил корень уравнения
х
3
+2
x
2+ 10
x =20 с ошибкой, меньшей чем
Численное решение алгебраических уравнений разбивается на следующие этапы: 1) выделение кратных корней, сводящее задачу к решению уравнения с простыми корнями; 2) определение границ, между которыми могут лежать корни уравнения; 3) разделение корней, т. е. указание промежутков, каждый из которых содержит не более одного простого корня (см. ); 4) грубое определение приближённого значения корня, выполняемое графически или каким-либо иным способом (например, при помощи изучения перемен знака левой части уравнения); 5) вычисление корня с заданной точностью. Наиболее распространёнными методами для этого являются методы ложного положения, метод Ньютона, , , разложение в ряды и т.д. При численном решении трансцендентных уравнений ограничиваются этапами 4 и 5. О численном решении дифференциальных уравнений см. в ст. дифференциальных уравнений. Лит.:Энциклопедия элементарной математики, кн. 2 - Алгебра, М.-Л., 1951; Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975. Численные методы Чи'сленные ме'тодыв математике, методы приближённого решения математических задач, сводящиеся к выполнению конечного числа элементарных операций над числами. В качестве элементарных операций фигурируют арифметические действия, выполняемые обычно приближённо, а также вспомогательные операции - записи промежуточных результатов, выборки из таблиц и т.п. Числа задаются ограниченным набором цифр в некоторой позиционной системе счисления (десятичной, двоичной и т.п.). Т. о., в Ч. м. числовая прямая заменяется дискретной системой чисел (сеткой); функция непрерывного аргумента заменяется таблицей её значений в сетке (см. ); операции анализа, действующие над непрерывными функциями, заменяются алгебраическими операциями над значениями функций в сетке. Ч. м. сводят решение математических задач к вычислениям, которые могут быть выполнены как вручную, так и с помощью вычислительных машин. Разработка новых Ч. м. и применение их в ЭВМ привели к возникновению . Числитель Числи'тельдроби m/n, число m, показывающее, из скольких долей 1/ n составлена . Числительное Числи'тельное,именная , общим лексическим значением которой является количество лиц или предметов. Грамматически Ч. характеризуется наличием категории (в языках с развитой морфологией), отчасти (в языках, имеющих грамматический род, некоторые Ч. обладают родовыми формами, например в русском языке «два», «две»), отсутствием категории .По характеру выражения количественного значения выделяются определённо-количественные Ч. (два, десять и т.п.) и неопределённо-количественные Ч. (много, мало и т.п.). Особую группу образуют собирательные Ч., обозначающие количество как совокупность (двое, трое, пятеро, оба). По структуре различаются простые (два, три, одиннадцать), сложные (пятьдесят, семьдесят) и составные Ч. (тридцать шесть, сто десять). Многие учёные считают прилагательными т. н. порядковые Ч. и слово «один», имеющие различия в числе и синтаксический род. Слова «десяток», «сотня», «тысяча», «миллион» относят к существительным, поскольку они обладают всеми признаками этой части речи. В истории славянских языков некоторые Ч. произошли от других частей речи (например, «пять» - существительное). Ч. следует отличать от других слов с количественным значением. Лит.:Супрун А. Е., Славянские числительные, Минск, 1969; Виноградов В. В., Русский язык, 2 изд., М., 1972. В. А. Виноградов. «Число» «Число'»,государственная налоговая система, введённая в 50-х гг. 13 в. на территориях, подвластных монгольским ханам. «Ч.» сменило откупную систему налогов с завоёванных монголами земель. При великом хане Менгу (1251-59) «Ч.» было введено в Китае, Средней Азии, Иране, Армении, было распространено на русские земли (Северо-Восточная Русь, Рязанское и Муромское княжества, Новгород Великий). Для этого монгольскими чиновниками были проведены переписи населения, которое делилось на десятки, сотни, тысячи и «тьмы» (10 тыс.). Служители церкви из переписи исключались. Лица, проводившие «Ч.», назывались численниками или писцами. Численники переписывали население по домам. Исчисление населения сопровождалось многочисленными злоупотреблениями и вызывало восстания (восстание в Новгороде Великом в 1257). На Руси деление населения по десятичной системе для уплаты налогов или экстраординарных ордынских сборов сохранялось вплоть до 15 в. Лит.:Насонов А. Н., Монголы и Русь, М.-Л., 1940; Павлов П. Н., К вопросу о русской дани в Золотую Орду, «Уч. зап. Красноярского гос. пед. института», т. 13. Серия историко-филологическая, в. 2, Красноярск. 1958. Число (в языкознании) Число'в языкознании, грамматическая категория, обозначающая в предложении количество участников действия ( и ) с помощью морфологических средств. Основным противопоставлением в категории Ч. является единственность - множественность. В некоторых языках имеется также двойственное Ч. и реже тройственное. С развитием языка двойственное Ч. может разрушаться и поглощаться множественными Ч., как это было в истории славянских языков (например в различались единственные, множественные и двойственные Ч.: «ты» - «вы» - «ва»). Среди форм и значений многие Ч. различаются множественное дистрибутивное (когда множество мыслится как состоящее из отдельных предметов, например «листы») и множественное собирательное (когда множество мыслится как единая совокупность, например «листья»). Собирательное значение может выражаться формой единственного Ч. («тряпьё», «вороньё»). Формы множественных Ч. могут также обозначать родовое понятие (родовое множественное Ч.), например «в этой местности водятся волки». Употребление формы множественного Ч. в значении единственного Ч. наблюдается в случаях вежливого множественного Ч. («вы» при обращении к одному лицу) и множественные Ч. величия («мы» в речи царствующих особ). Как независимая категория Ч. свойственно существительным и личным местоимениям, другие (глагол, прилагательное, прочие разряды местоимений) получают числовые характеристики по (синтаксическое Ч.). Согласование по числу обязательно в : «он работает» - «они работают», англ. he works - they work. Однако с разрушением морфологии согласование также может исчезать, например в английском языке уже нет согласования по Ч. между прилагательным и существительным (clever child - «умный ребёнок» - clever children - «умные дети»). Способы выражения множественных Ч. различны: аффиксальное Ч. («стол» - «столы», англ. table - tables), супплетивное Ч. («человек» - «люди»), см. ; ломаное Ч. (араб. rad~ulun - «мужчина», rid~alun - «мужчины»; изменяется огласовка корня); множественное Ч. с повтором (индонез. оранг - «человек», оранг-оранг - «люди»). В индоевропейских языках форма множественного Ч. обязательна, если существительное имеет при себе количественное слово (десять книг, много книг). В некоторых языках существительное в таких конструкциях употребляется в форме единственного Ч. (венг. kцnyv - «книга», tiz kцnyv - «10 книг», sok kцnyv - «много книг»). Во многих языках Азии и Америки для выражения множественного Ч. существительных в конструкции с числительным используются специальные элементы - классификаторы (нумеративы), различные для разных лексических групп существительных; последние при этом своей формы не меняют (вьетнамский яз. hai con meo - «две кошки», где con - классификатор). Лит.:Сепир Э., Язык, пер. с англ., М.-Л., 1934; Есперсен О., Философия грамматики, пер. с англ., М., 1958; Реформатский А. А., Число и грамматика, сб.: Вопросы грамматики, М.-Л., 1960; Виноградов В. В., Русский язык, 2 изд., М., 1972. В. А. Виноградов. Число (матем.) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 |
|||||||
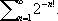
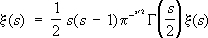
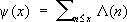
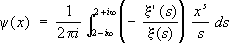
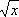 ln
2
x),
ln
2
x),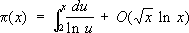
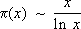
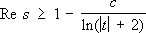
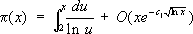
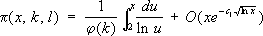
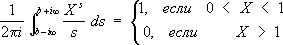
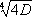 , и существуют такие формы, минимумы которых равны
, и существуют такие формы, минимумы которых равны
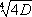 .Примером такой формы является следующая:
.Примером такой формы является следующая: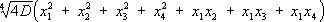 .
.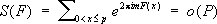 ,
,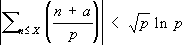 ,
X> 0,
,
X> 0,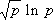 , асимптотически поровну. Кроме того, он высказал гипотезу, что это будет верно при
Х > р
e, где e > 0 - сколь угодно малое число. В 1917 И. М. Виноградов доказал, что число целых точек в области 0
< yЈ
f(
x),
a < xЈ
b, при определённых ограничениях на порядок роста второй производной
f(
x), равно площади этой области с точностью до слагаемого порядка корня кубического из главного члена. Позднее чешским математиком В. Ярником установлено, что точность этой формулы при сделанных предположениях относительно
f(
x) нельзя существенно улучшить.
, асимптотически поровну. Кроме того, он высказал гипотезу, что это будет верно при
Х > р
e, где e > 0 - сколь угодно малое число. В 1917 И. М. Виноградов доказал, что число целых точек в области 0
< yЈ
f(
x),
a < xЈ
b, при определённых ограничениях на порядок роста второй производной
f(
x), равно площади этой области с точностью до слагаемого порядка корня кубического из главного члена. Позднее чешским математиком В. Ярником установлено, что точность этой формулы при сделанных предположениях относительно
f(
x) нельзя существенно улучшить.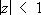 ,
,
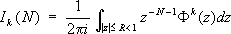 .
.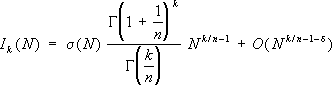
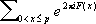 ,
,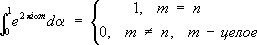
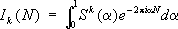 ,
,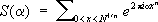 .
.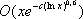 ,
c> 0,
,
c> 0,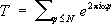 .
.
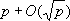 решений (теорема Хассе - Вейля).
решений (теорема Хассе - Вейля).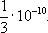 В конце 16 в. И. Бюрги (Швейцария) вычислил корень уравнения 9 - 30
x
2+ 27
x
4
-9
x
6
+
x
8
=0, определяющего длину стороны правильного девятиугольника. Приблизительно в то же время Ф.
дал метод вычисления корней алгебраических уравнений, сходный с
.
В конце 16 в. И. Бюрги (Швейцария) вычислил корень уравнения 9 - 30
x
2+ 27
x
4
-9
x
6
+
x
8
=0, определяющего длину стороны правильного девятиугольника. Приблизительно в то же время Ф.
дал метод вычисления корней алгебраических уравнений, сходный с
.